【蓝桥杯刷题】坑爹的负进制转换
【蓝桥杯刷题】——坑爹的负进制转换😎😎😎
目录
💡前言🌞:
💛坑爹的负进制转换题目💛
💪 解题思路的分享💪
😊题目源码的分享😊
👉 本菜鸡&总结 👈
😎博客昵称:陈大大陈
😊座右铭:所谓觉悟,就是在漆黑的荒野上开辟出一条理当前进的光明大道。
😋博主简介:一名热爱C/C++和算法等技术,喜欢运动,爱胡思乱想却胸怀大志的小博主!
😚博主&唠嗑:早中晚安!😄各位CSDN的朋友!😄我是博客新人陈大大陈,希望我的文章能为你带来帮助!欢迎大家在评论区畅所欲言!也希望大家多多为我提出您宝贵的建议!😘如果觉得我写的不错的话还请点个赞和关注哦~😘😘😘
💡前言🌞:
大伙们好!😄又到了小陈蓝桥杯每日一题的时间了~ 😋😋😋今天也带来了十分有趣的题目!🥰🥰🥰用C语言实现——坑爹的负进制转换,这个题目对我来说很有挑战性,把我折磨的很难受,不过我还是整出来了,我现在迫不及待地要和大家分享~!😄🤗🤗
💛坑爹的负进制转换题目💛
💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡💡
题目描述
以前我们做的进制转换大家都忽略了一点,就是进制一定是正整数;今天这道进制转换就坑爹的选择了,额,负整数来做进制。
输入描述
输入由若干行组成,每行有两个整数n(-32765<=n<=32767)和R(-16<=R<=-2)。输入的最后一行只有一个‘#’号,表示输入结束。
输出描述
对于每个输入行,输出n的R进制形式。出现的字母请用大写字母表示!
样例输入
30000 -2 -20000 -2 28800 -16 -25000 -16 #样例输出
11011010101110000 1111011000100000 19180 7FB8
💪 解题思路的分享💪
- 我们采用递归的写法来写这道题目。
- 首先我们要知道,在C语言中,商和余数都符合 被除数=商x除数+余数 这一数学规律。C/C++ 是向零取整(负数向上、正数向下取整)的。也就是说,余数可能是负数。
- 我们要打印出对应的负二进制,就不能有负数,所以代码中如果余数为负数,要将其变为正数。
- 说道递归,那就必须要有出口,我们将a==0作为递归出口,当a不停除以对应进制到零,此时递归停止。
- 当余数小于零时,我们该如何将其变为正数呢?例如-5/-2=2余-1,这个-1没有办法处理。
- 我们不能改变结果的值,那就需要一个看起来很简单但是想不到的转换公式:
- (商+1)*除数+(余数-除数)=商*除数+除数+余数-除数=商*除数+余数=被除数
- 所以我们要保证商不变的话只要 被除数=被除数+除数,化简一下可以得到商=被除数/除数--->(被除数+除数)/除数=商+1 。
- 为了实现多组输入,用scanf返回值来判断输入是否正确。
😊题目源码的分享😊
#define _CRT_SECURE_NO_WARNINGS
#include<stdio.h>
void JinZhi(int a, int b)
{if (a == 0)return;//递归的出口int m = a % b;if (m < 0){m -= b; a += b;}if (m > 10){m = m - 10 + 'A';//转化成字符型,方便16进制输出成字符}else{m += '0';}JinZhi(a / b, b);printf("%c", m);//注意顺序,不要写到函数的前面,不然就反了
}
int main()
{int n[10], m[10],i=0;int a, b;while (scanf("%d%d", &a, &b) == 2)//用scanf返回值来判断输入是否正确{n[i] = a;m[i] = b;i++;}for (int j = 0; j < i; j++){JinZhi(n[j], m[j]);printf("\n");}return 0;
}👉 本菜鸡&总结 👈
这是我们学校蓝桥杯选拔赛上面的题目,我觉得很有挑战性写了这篇博客,这种题目比较耐人寻味,哪位大佬有更好的做法,请在评论区不吝赐教哦~😀如果觉得我写的不错的话还请点个赞和关注哦~我会持续输出编程的知识的!🌞🌞🌞
相关文章:

【蓝桥杯刷题】坑爹的负进制转换
【蓝桥杯刷题】——坑爹的负进制转换😎😎😎 目录 💡前言🌞: 💛坑爹的负进制转换题目💛 💪 解题思路的分享💪 😊题目源码的分享Ƕ…...

react+antdpro+ts实现企业级项目二:Strapi及认证登陆模块
在上一章节中,我们已经成功创建并登陆了系统,现在需要为系统添加权限和登录认证,以提高系统的安全性、数据保护、个性化服务和用户体验。此外,添加权限和登录认证还可以方便管理员进行用户和授权管理。为了快速开发前端࿰…...

Android ANR trace日志如何导出
什么是ANR ?上网搜索,一搜一大片,我就说个很容易识别的字眼,XXXAPP无响应 ANR trace日志如何导出?使用ADB命令: adb pull data/anr/trace.txt 你要存放的路径。查看ANR报错位置全局搜索你APP的包名&#x…...

Windows SSH 配置和SCP的使用
使用用户界面安装 ssh 功能 要在 Windows 10/11 上启用 SSH 服务器,请按照以下步骤操作: 按“Windows 键 I”打开“设置”菜单,然后选择“应用程序”。在左侧菜单栏中选择“应用和功能”。从列表中选择“可选功能”。 点击“添加功能”按钮…...

liunx 安装redsi和连接
liunx 安装redsi和连接 下载 (https://download.redis.io/releases/) 上传到 /usr/local目录 解压 tar -xvf redis-5.0.14.tar.gz 切换到 cd ./redis-5.0.14 编译 make 安装 make install 默认安装目录 /usr/local/bin/ 修改 ./redis-5.0.14/reds…...
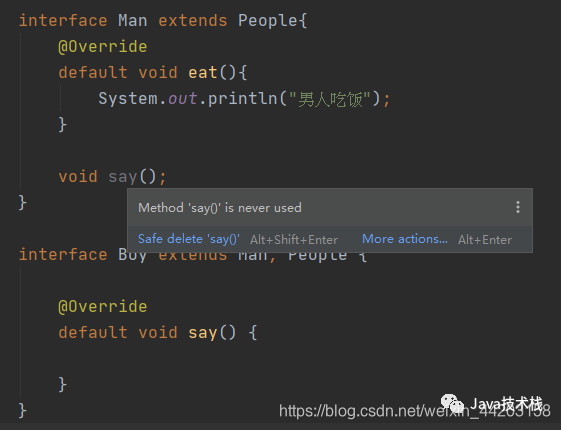
接口里面可以写实现方法吗【可以】 、接口可以多继承吗【可以】
比如下面这道题: 问: 接口里面可以写方法吗? 答: 当然可以啊,默认就是抽象方法。 . 问: 那接口里面可以写实现方法吗? 答: 不可以,所有方法必须是抽象的。 . 问: 你确定吗࿱…...
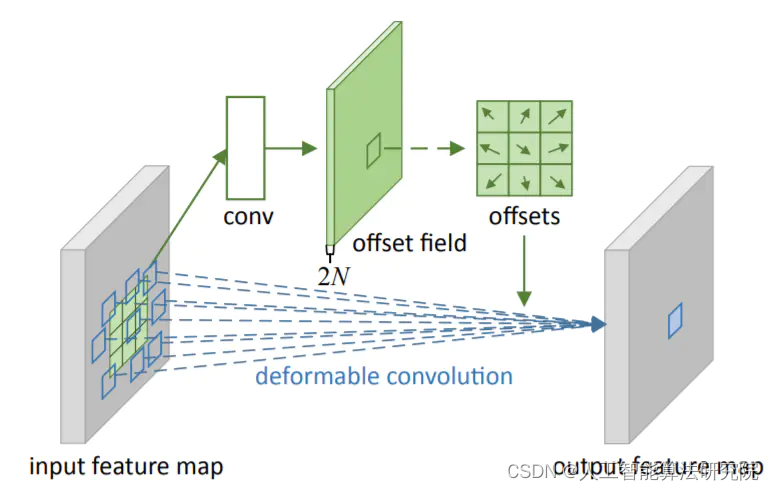
【YOLOv8/YOLOv7/YOLOv5/YOLOv4/Faster-rcnn系列算法改进NO.57】引入可形变卷积
文章目录前言一、解决问题二、基本原理三、添加方法四、总结前言 作为当前先进的深度学习目标检测算法YOLOv8,已经集合了大量的trick,但是还是有提高和改进的空间,针对具体应用场景下的检测难点,可以不同的改进方法。此后的系列…...
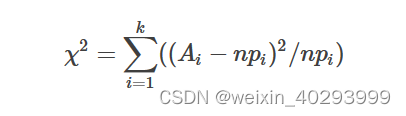
统计学习--三种常见的相关系数
1)Pearson积差相关系数:用于量度两个变量X和Y之间的线性相关。它具有1和-1之间的值,其中1是总正线性相关性,0是非线性相关性,并且-1是总负线性相关性。Pearson相关系数的一个关键数学特性是它在两个变量的位置和尺度的…...
基于Django4.1.4的入门学习记录
基于Django4.1.4的入门学习记录Django创建Django项目创建工程工程目录说明运行开发服务器settings.py配置文件应用的创建创建应用模块应用模块文件说明App应用配置注册安装子应用数据模型ORM概述定义模型类生成数据库表查看数据库文件Admin管理工具管理界面本地化创建管理员注册…...

C++ Butterworth N阶滤波器设计
介绍一个 Butterworth Nth 滤波器设计系数的函数,像 Matlab 函数一样的: [bl,al]butter(but_order,Ws); 和 [bh,ah]butter(but_order,2*bandwidth(1)/fs,high);rtfilter 在 Ububtu 中,容易找到: $ aptitude search ~dbutterwo…...

UXP下不用任何框架创建自己的插件并试运行
在上一篇文章中《Windows下vue框架下的UXP插件开发环境搭建及程序试运行》,搭建的是利用vue框架进行开发的UXP开发环境,而且是把官方的案例插件直接添加进UDT,下面要说的是不利用任何js的框架创建和试运行自己的UXP插件程序,这样来…...

mac修改国内源快速安装brew
我是参考了清华源官网,有任何困惑直接访问该网址即可。这里给出精简版。 1. 更改镜像到~/.zshrc 终端添加方式 echo export HOMEBREW_API_DOMAIN"https://mirrors.tuna.tsinghua.edu.cn/homebrew-bottles/api" >> ~/.zshrcecho export HOMEBREW_…...

Me-and-My-Girlfriend-1靶场通关
Me-and-My-Girlfriend-1靶场通关 靶机ip:192.168.112.135 信息收集 端口:22、80 还是从80WEB服务器端口入手 对服务器目录进行扫描,扫出以下目录 访问80端口WEB服务,显示一段文字只允许本地用户访问。 一眼伪造ip,查看页面…...

2.6 棋盘覆盖
在一个2*x2‘个方格组成的棋盘中,若怡有一个方格与其他方格不同,则称该方格为特殊方格,且称该棋盘为一特殊棋盘。显然,特殊方格在棋盘上出现的位置有 4种情形因而对任何k0,有4‘种特殊棋盘。图2-4 申的特殊棋益是12时 …...

JMU软件20 大数据技术复习(只写了对比18提纲的变动部分)
原博主 博客主页:https://xiaojujiang.blog.csdn.net/ 原博客链接:https://blog.csdn.net/qq_43058685/article/details/117883940 本复习提纲只适用于JMU软件工程大数据课程(ckm授课) 具体内容参考老师提纲的考纲,18和…...

MySQL底层存储B-Tree和B+Tree原理分析
1.B-Tree的原理分析 (1)什么是B-Tree B-树,全称是 Balanced Tree,是一种多路平衡查找树。 一个节点包括多个key (数量看业务),具有M阶的B树,每个节点最多有M-1个Key。 节点的key元素个数就是指这个节点能…...

基于Vue+Vue-cli+webpack搭建渐进式高可维护性前端实战项目
本文是专栏《手把手带你做一套毕业设计毕业设计》的实战第一篇,将从Vue脚手架安装开始,逐步带你搭建起一套管理系统所需的架构。当然,在默认安装完成之后,会对文件目录进行初步的细化拆分,以便后续功能迭代和维护所用。…...

第十三章:Java反射机制
第十三章:Java反射机制 13.1:Java反射机制概述 Java Reflection Reflection(反射)是被视为动态语言的关键,反射机制允许程序在执行期借助于Reflection API取得任何类的内部信息,并能直接操作任意对象的内部属性及方法。 加…...

iLok USB不识别怎么办?
我的iLok USB坏了吗? 我的iLok USB没有被系统或软件识别。 如果您的iLok USB未被识别,问题可能出在iLok USB、iLok软件或受保护的软件。 提示如果您使用USB集线器,请确保您使用正确的集线器电源适配器。排除硬件:将iLok USB直接插…...
【LeetCode与《代码随想录》】二叉树篇:做题笔记与总结-JavaScript版
文章目录代码随想录144. 二叉树的前序遍历94. 二叉树的中序遍历145. 二叉树的后序遍历102.二叉树的层序遍历226.翻转二叉树101. 对称二叉树104.二叉树的最大深度111.二叉树的最小深度222.完全二叉树的节点个数110.平衡二叉树257. 二叉树的所有路径404.左叶子之和513.找树左下角…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

抖音增长新引擎:品融电商,一站式全案代运营领跑者
抖音增长新引擎:品融电商,一站式全案代运营领跑者 在抖音这个日活超7亿的流量汪洋中,品牌如何破浪前行?自建团队成本高、效果难控;碎片化运营又难成合力——这正是许多企业面临的增长困局。品融电商以「抖音全案代运营…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

[免费]微信小程序问卷调查系统(SpringBoot后端+Vue管理端)【论文+源码+SQL脚本】
大家好,我是java1234_小锋老师,看到一个不错的微信小程序问卷调查系统(SpringBoot后端Vue管理端)【论文源码SQL脚本】,分享下哈。 项目视频演示 【免费】微信小程序问卷调查系统(SpringBoot后端Vue管理端) Java毕业设计_哔哩哔哩_bilibili 项…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...

Web中间件--tomcat学习
Web中间件–tomcat Java虚拟机详解 什么是JAVA虚拟机 Java虚拟机是一个抽象的计算机,它可以执行Java字节码。Java虚拟机是Java平台的一部分,Java平台由Java语言、Java API和Java虚拟机组成。Java虚拟机的主要作用是将Java字节码转换为机器代码&#x…...

多模态图像修复系统:基于深度学习的图片修复实现
多模态图像修复系统:基于深度学习的图片修复实现 1. 系统概述 本系统使用多模态大模型(Stable Diffusion Inpainting)实现图像修复功能,结合文本描述和图片输入,对指定区域进行内容修复。系统包含完整的数据处理、模型训练、推理部署流程。 import torch import numpy …...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

