统计学习--三种常见的相关系数
1)Pearson积差相关系数:用于量度两个变量X和Y之间的线性相关。它具有+1和-1之间的值,其中1是总正线性相关性,0是非线性相关性,并且-1是总负线性相关性。Pearson相关系数的一个关键数学特性是它在两个变量的位置和尺度的单独变化下是不变的。也就是说,我们可以将X变换为a+bX并将Y变换为c+dY,而不改变相关系数,其中a,b,c和d是常数,b,d > 0。请注意,更一般的线性变换确实会改变相关性。
Pearson积差相关系数对应的计算公式如下:
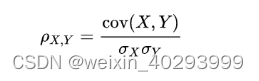
积差相关系数的适用条件: 在相关分析中首先要考虑的问题就是两个变量是否可能存在相关关系,如果得到了肯定的结论,那才有必要进行下一步定量的分析。另外还必须注意以下几个问题:
1、 积差相关系数适用于线性相关的情形,对于曲线相关等更为复杂的情形,积差相关系数的大小并不能代表相关性的强弱。
2、 样本中存在的极端值对Pearson积差相关系数的影响极大,因此要慎重考虑和处理,必要时可以对其进行剔出,或者加以变量变换,以避免因为一两个数值导致出现错误的结论。 3、 Pearson积差相关系数要求相应的变量呈双变量正态分布,注意双变量正态分布并非简单的要求x变量和y变量各自服从正态分布,而是要求服从一个联合的双变量正态分布。 以上几条要求中,前两者的要求最严,第三条比较宽松,违反时系数的结果也是比较稳健的。
2)Spearman秩相关系数:使利用两变量的秩次大小作线性相关分析,对原始变量的分布不做要求,属于非参数统计方法。因此它的适用范围比Pearson相关系数要广的多。即使原始数据是等级资料也可以计算Spearman相关系数。对于服从Pearson相关系数的数据也可以计算Spearman相关系数,但统计效能比Pearson相关系数要低一些(不容易检测出两者事实上存在的相关关系)。如果数据中没有重复值, 并且当两个变量完全单调相关时,斯皮尔曼相关系数则为+1或−1。Spearman相关系数即使出现异常值,由于异常值的秩次通常不会有明显的变化(比如过大或者过小,那要么排第一,要么排最后),所以对Spearman相关性系数的影响也非常小。
计算公式:对于样本容量为n的样本,n个原始数据被转换成等级数据,相关系数ρ为
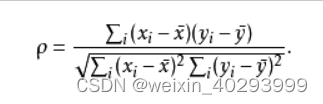
实际应用中,变量间的连结是无关紧要的,于是可以通过简单的步骤计算ρ.被观测的两个变量的等级的差值,则ρ为
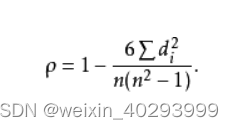
3)Kendall秩相关系数: 是一种秩相关系数,用于反映分类变量相关性的指标,适用于两个变量均为有序分类的情况,用希腊字母τ(tau)表示其值。
【分类变量可以理解成有类别的变量,可以分为无序的,比如性别(男、女)、血型(A、B、O、AB);有序的,比如肥胖等级(重度肥胖,中度肥胖、轻度肥胖、不肥胖)。通常需要求相关性系数的都是有序分类变量】
Kendall相关系数的取值范围在-1到1之间,当τ为1时,表示两个随机变量拥有一致的等级相关性;当τ为-1时,表示两个随机变量拥有完全相反的等级相关性;当τ为0时,表示两个随机变量是相互独立的。
计算公式:Kendall系数是基于协同的思想。对于X,Y的两对观察值Xi,Yi和Xj,Yj,如果Xi<Yi并且Xj<Yj,或者Xi>Yi并且Xj>Yj,则称这两对观察值是和谐的,否则就是不和谐。kendall相关系数的计算公式如下:

和谐的观察值对减去不和谐的观察值对的数量,除以总的观察值对数.
注意:三种相关系数都是对变量之间相关程度的度量,由于其计算方法不一样,用途和特点也不一样。
1)Pearson相关系数是在原始数据的方差和协方差基础上计算得到,所以对离群值比较敏感,它度量的是线性相关。因此,即使pearson相关系数为0,也只能说明变量之间不存在线性相关,但仍有可能存在曲线相关。
2)Spearman相关系数和kendall相关系数都是建立在秩和观测值的相对大小的基础上得到,是一种更为一般性的非参数方法,对离群值的敏感度较低,因而也更具有耐受性,度量的主要是变量之间的联系。
补充:无序分类变量的统计推断:卡方检验
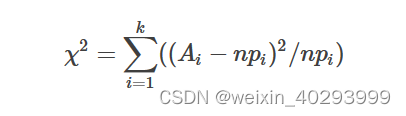
Ai为i水平的观测频数,Ei为i水平的期望频数,n为总频数,Pi为i水平的期望概率。 主要用于检验某无序分类变量各水平在两组或多组间的分布是否一致。还可以用于检验一个分类变量各水平出现的概率是否等于指定概率;一个连续变量的分布是否符合某种理论分布等。其主要用途:
1、 检验某个连续变量的分布是否与某种理论分布相一致。
2、 检验某个分类变量各类的出现概率是否等于制定概率。
3、 检验某两个分类变量是否相互独立。
4、 检验控制某种或某几种分类因素的作用以后,另两个分类变量是否相互独立。
5、 检验某两种方法的结果是否一致。
相关文章:
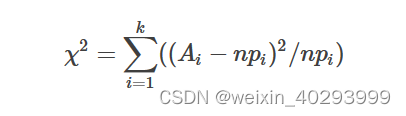
统计学习--三种常见的相关系数
1)Pearson积差相关系数:用于量度两个变量X和Y之间的线性相关。它具有1和-1之间的值,其中1是总正线性相关性,0是非线性相关性,并且-1是总负线性相关性。Pearson相关系数的一个关键数学特性是它在两个变量的位置和尺度的…...
基于Django4.1.4的入门学习记录
基于Django4.1.4的入门学习记录Django创建Django项目创建工程工程目录说明运行开发服务器settings.py配置文件应用的创建创建应用模块应用模块文件说明App应用配置注册安装子应用数据模型ORM概述定义模型类生成数据库表查看数据库文件Admin管理工具管理界面本地化创建管理员注册…...

C++ Butterworth N阶滤波器设计
介绍一个 Butterworth Nth 滤波器设计系数的函数,像 Matlab 函数一样的: [bl,al]butter(but_order,Ws); 和 [bh,ah]butter(but_order,2*bandwidth(1)/fs,high);rtfilter 在 Ububtu 中,容易找到: $ aptitude search ~dbutterwo…...

UXP下不用任何框架创建自己的插件并试运行
在上一篇文章中《Windows下vue框架下的UXP插件开发环境搭建及程序试运行》,搭建的是利用vue框架进行开发的UXP开发环境,而且是把官方的案例插件直接添加进UDT,下面要说的是不利用任何js的框架创建和试运行自己的UXP插件程序,这样来…...

mac修改国内源快速安装brew
我是参考了清华源官网,有任何困惑直接访问该网址即可。这里给出精简版。 1. 更改镜像到~/.zshrc 终端添加方式 echo export HOMEBREW_API_DOMAIN"https://mirrors.tuna.tsinghua.edu.cn/homebrew-bottles/api" >> ~/.zshrcecho export HOMEBREW_…...

Me-and-My-Girlfriend-1靶场通关
Me-and-My-Girlfriend-1靶场通关 靶机ip:192.168.112.135 信息收集 端口:22、80 还是从80WEB服务器端口入手 对服务器目录进行扫描,扫出以下目录 访问80端口WEB服务,显示一段文字只允许本地用户访问。 一眼伪造ip,查看页面…...

2.6 棋盘覆盖
在一个2*x2‘个方格组成的棋盘中,若怡有一个方格与其他方格不同,则称该方格为特殊方格,且称该棋盘为一特殊棋盘。显然,特殊方格在棋盘上出现的位置有 4种情形因而对任何k0,有4‘种特殊棋盘。图2-4 申的特殊棋益是12时 …...

JMU软件20 大数据技术复习(只写了对比18提纲的变动部分)
原博主 博客主页:https://xiaojujiang.blog.csdn.net/ 原博客链接:https://blog.csdn.net/qq_43058685/article/details/117883940 本复习提纲只适用于JMU软件工程大数据课程(ckm授课) 具体内容参考老师提纲的考纲,18和…...

MySQL底层存储B-Tree和B+Tree原理分析
1.B-Tree的原理分析 (1)什么是B-Tree B-树,全称是 Balanced Tree,是一种多路平衡查找树。 一个节点包括多个key (数量看业务),具有M阶的B树,每个节点最多有M-1个Key。 节点的key元素个数就是指这个节点能…...

基于Vue+Vue-cli+webpack搭建渐进式高可维护性前端实战项目
本文是专栏《手把手带你做一套毕业设计毕业设计》的实战第一篇,将从Vue脚手架安装开始,逐步带你搭建起一套管理系统所需的架构。当然,在默认安装完成之后,会对文件目录进行初步的细化拆分,以便后续功能迭代和维护所用。…...

第十三章:Java反射机制
第十三章:Java反射机制 13.1:Java反射机制概述 Java Reflection Reflection(反射)是被视为动态语言的关键,反射机制允许程序在执行期借助于Reflection API取得任何类的内部信息,并能直接操作任意对象的内部属性及方法。 加…...

iLok USB不识别怎么办?
我的iLok USB坏了吗? 我的iLok USB没有被系统或软件识别。 如果您的iLok USB未被识别,问题可能出在iLok USB、iLok软件或受保护的软件。 提示如果您使用USB集线器,请确保您使用正确的集线器电源适配器。排除硬件:将iLok USB直接插…...
【LeetCode与《代码随想录》】二叉树篇:做题笔记与总结-JavaScript版
文章目录代码随想录144. 二叉树的前序遍历94. 二叉树的中序遍历145. 二叉树的后序遍历102.二叉树的层序遍历226.翻转二叉树101. 对称二叉树104.二叉树的最大深度111.二叉树的最小深度222.完全二叉树的节点个数110.平衡二叉树257. 二叉树的所有路径404.左叶子之和513.找树左下角…...

机器人运动|浅谈Time Elastic Band算法
前言在自主移动机器人路径规划的学习与开发过程中,我接触到Time Elastic Band算法,并将该算法应用于实际机器人,用于机器人的局部路径规划。在此期间,我也阅读了部分论文、官方文档以及多位大佬的文章,在此对各位大佬的…...

【Linux】网络基础(1)
前言 相信没有网络就没有现在丰富的世界。本篇笔记记录我在Linux系统下学习网络基础部分知识,从关于网络的各种概念和关系开始讲起,逐步架构起对网络的认识,对网络编程相关的认知。 我的上一篇Linux文章呀~ 【Linux】网络套接字编程_柒海啦的…...

限流算法详解
限流是我们经常会碰到的东西,顾名思义就是限制流量。它能保证我们的系统不会被突然的流量打爆,保证系统的稳定运行。像我们生活中,地铁就会有很多护栏,弯弯绕绕的,这个就是一种限流。像我们抢茅台,肯定大部…...
Spark/Hive
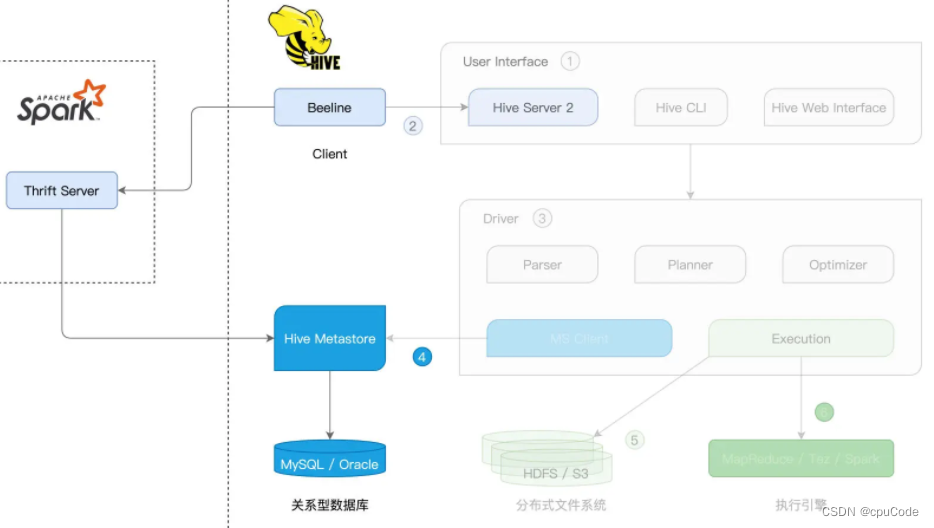
Spark/HiveHive 原理Spark with HiveSparkSession Hive Metastorespark-sql CLI Hive MetastoreBeeline Spark Thrift ServerHive on SparkHive 擅长元数据管理Spark 擅长高效的分布式计算 Spark Hive 集成 : Hive on Spark : Hive 用 Spark 作为底层的计算引擎时Spark w…...
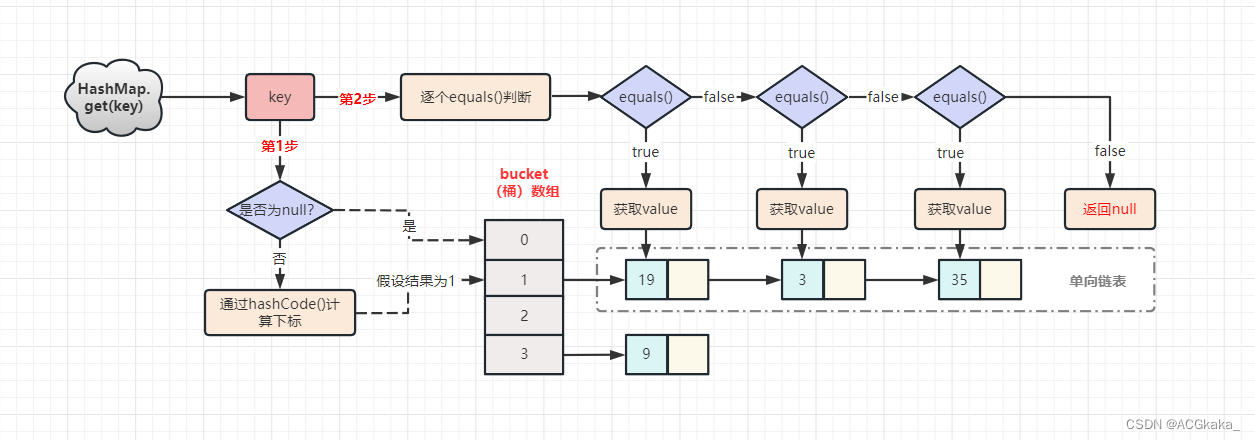
HashMap底层的实现原理(JDK8)
目录一、知识点回顾二、HashMap 的 put() 和 get() 的实现2.1 map.put(k, v) 实现原理2.2 map.get(k) 实现原理三、HashMap 的常见面试题3.1 为何随机增删、查询效率都很高?3.2 为什么放在 HashMap 集合 key 部分的元素需要重写 equals 方法?3.3 HashMap 的 key 为…...
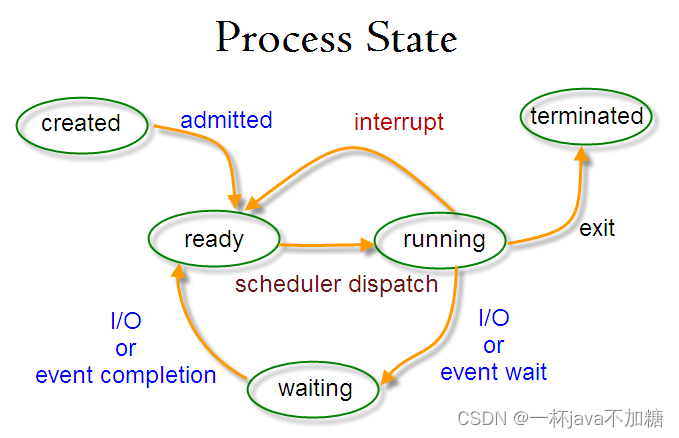
操作系统-整理
进程 介绍 进程是系统进行资源分配和调度的一个独立单位。每个进程都有自己的独立内存空间,不同进程通过进程间通信来通信。由于进程占据独立的内存,所以上下文进程间的切换开销(栈、寄存器、虚拟内存、文件句柄等)比较大&#…...
系统换行符的思考
各系统换行符 换行符,也即是回车换行,因为表示为Carriage-Return和Line-Feed。 回车用Return-Carrige表示,简写为CR,字符表示为\r。 换行用Line-Feed表示,简写为LF,字符表示为\n。 由于历史原因…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

拉力测试cuda pytorch 把 4070显卡拉满
import torch import timedef stress_test_gpu(matrix_size16384, duration300):"""对GPU进行压力测试,通过持续的矩阵乘法来最大化GPU利用率参数:matrix_size: 矩阵维度大小,增大可提高计算复杂度duration: 测试持续时间(秒&…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

基于Java+MySQL实现(GUI)客户管理系统
客户资料管理系统的设计与实现 第一章 需求分析 1.1 需求总体介绍 本项目为了方便维护客户信息为了方便维护客户信息,对客户进行统一管理,可以把所有客户信息录入系统,进行维护和统计功能。可通过文件的方式保存相关录入数据,对…...
