力扣练习题(2024/4/16)
1买卖股票的最佳时机
给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。
你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。
返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润,返回 0 。
示例 1:
输入:[7,1,5,3,6,4] 输出:5 解释:在第 2 天(股票价格 = 1)的时候买入,在第 5 天(股票价格 = 6)的时候卖出,最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格;同时,你不能在买入前卖出股票。
示例 2:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 没有交易完成, 所以最大利润为 0。
提示:
1 <= prices.length <= 1050 <= prices[i] <= 104
思路1暴力解法:
暴力解法的思路是遍历所有可能的买入和卖出时机,并计算它们之间的利润,然后找出利润最大的情况。具体步骤如下:
-
遍历所有可能的买入和卖出时机:使用两重循环,外层循环遍历可能的买入时机,内层循环在外层循环中的每个买入时机后面遍历可能的卖出时机。
-
计算利润:对于每一对买入和卖出时机,计算卖出价格减去买入价格得到的利润。
-
找出最大利润:在遍历过程中不断更新最大利润,并记录对应的买入和卖出时机。
-
返回结果:最终返回最大利润及对应的买入和卖出时机。
代码:
class Solution {
public:// 计算股票的最大利润int maxProfit(vector<int>& prices) {int result = 0; // 初始化最大利润为0for (int i = 0; i < prices.size(); i++) { // 遍历所有可能的买入时机for (int j = i + 1; j < prices.size(); j++){ // 在每个买入时机后面遍历可能的卖出时机result = max(result, prices[j] - prices[i]); // 计算当前买入和卖出时机的利润并更新最大利润}}return result; // 返回最大利润}
};思路2:
解题思路是基于动态规划的思想。首先,我们定义了一个二维动态规划数组 dp,其中 dp[i][0] 表示第 i 天不持有股票时的最大利润,dp[i][1] 表示第 i 天持有股票时的最大利润。然后,我们通过遍历股票价格列表,在每一天都更新 dp 数组的值,直到遍历完所有的天数。
在更新 dp 数组的过程中,我们根据状态转移方程进行更新。对于第 i 天,有两种情况:
- 如果第 i 天不持有股票,则其最大利润为前一天不持有股票的利润
dp[i-1][0],或者是前一天持有股票,然后在第 i 天卖出股票得到的利润dp[i-1][1] + prices[i]的较大值。 - 如果第 i 天持有股票,则其最大利润为前一天持有股票的利润
dp[i-1][1],或者是前一天不持有股票,然后在第 i 天买入股票得到的利润-prices[i]的较大值。
根据以上思路,我们在循环中更新 dp 数组的值,最终返回最后一天不持有股票时的最大利润,即 dp[len-1][0]。
注意这里说的是“持有”,“持有”不代表就是当天“买入”!也有可能是昨天就买入了,今天保持持有的状态
dp数组如何初始化
由递推公式 dp[i][0] = max(dp[i - 1][0], -prices[i]); 和 dp[i][1] = max(dp[i - 1][1], prices[i] + dp[i - 1][0]);可以看出
其基础都是要从dp[0][0]和dp[0][1]推导出来。
那么dp[0][0]表示第0天持有股票,此时的持有股票就一定是买入股票了,因为不可能有前一天推出来,所以dp[0][0] -= prices[0];
dp[0][1]表示第0天不持有股票,不持有股票那么现金就是0,所以dp[0][1] = 0;
代码:
class Solution {
public:// 计算股票的最大利润int maxProfit(vector<int>& prices) {int len = prices.size(); // 获取股票价格列表的长度if (len == 0) {return 0; // 如果列表为空,返回0}vector<vector<int>> dp(len, vector<int>(2)); // 定义二维动态规划数组dpfor (int i = 0; i < len; i++) {// 根据状态转移方程填充dp数组if (i == 0) {dp[i][0] = 0;dp[i][1] = -prices[i]; // 第一天持有股票的利润为 -prices[i]} else {// 不持有股票的利润为前一天不持有股票的利润与前一天持有股票今天卖出的利润的较大值dp[i][0] = max(dp[i-1][0], dp[i-1][1] + prices[i]);// 持有股票的利润为前一天持有股票的利润与今天买入股票的利润的较大值dp[i][1] = max(dp[i-1][1], -prices[i]); // -prices[i] 表示买入股票的利润}}return dp[len-1][0]; // 返回最后一天持有股票获得的利润}
};2买卖股票的最佳时机 II
给你一个整数数组 prices ,其中 prices[i] 表示某支股票第 i 天的价格。
在每一天,你可以决定是否购买和/或出售股票。你在任何时候 最多 只能持有 一股 股票。你也可以先购买,然后在 同一天 出售。
返回 你能获得的 最大 利润 。
示例 1:
输入:prices = [7,1,5,3,6,4] 输出:7 解释:在第 2 天(股票价格 = 1)的时候买入,在第 3 天(股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。随后,在第 4 天(股票价格 = 3)的时候买入,在第 5 天(股票价格 = 6)的时候卖出, 这笔交易所能获得利润 = 6 - 3 = 3 。总利润为 4 + 3 = 7 。
示例 2:
输入:prices = [1,2,3,4,5] 输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5 - 1 = 4 。总利润为 4 。
示例 3:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这种情况下, 交易无法获得正利润,所以不参与交易可以获得最大利润,最大利润为 0 。
提示:
1 <= prices.length <= 3 * 1040 <= prices[i] <= 104
思路:
- dp[i][0] 表示第i天持有股票所得现金。
- dp[i][1] 表示第i天不持有股票所得最多现金
重点:
-
首先,定义一个二维动态规划数组
dp,其中dp[i][0]表示第 i 天不持有股票时的最大利润,dp[i][1]表示第 i 天持有股票时的最大利润。 -
初始条件设定为第一天,即
dp[0][0]表示第一天持有股票的利润为负的第一天股票价格,dp[0][1]表示第一天不持有股票的利润为0。 -
然后,利用状态转移方程进行动态规划。遍历股票价格列表,对于每一天的状态,更新
dp数组的值。 -
对于
dp[i][0],表示第 i 天不持有股票时的最大利润,可以选择在前一天不持有股票的情况下保持不动,或者在前一天持有股票的情况下在第 i 天卖出股票。因此,取两者之间的较大值作为dp[i][0]的值。 -
对于
dp[i][1],表示第 i 天持有股票时的最大利润,可以选择在前一天持有股票的情况下保持不动,或者在前一天不持有股票的情况下在第 i 天买入股票。同样,取两者之间的较大值作为dp[i][1]的值。 -
最终,返回
dp[len - 1][1],表示最后一天不持有股票获得的最大利润,即为问题的解。
dp[i - 1][0]表示第 i - 1 天不持有股票时的最大利润,即前一天的利润。dp[i - 1][1] - prices[i]表示前一天持有股票时的最大利润减去第 i 天股票价格后的值,即前一天持有股票,然后在第 i 天卖出股票得到的利润。
因此,max(dp[i - 1][0], dp[i - 1][1] - prices[i]) 取了这两者之间的较大值,即在第 i 天不持有股票时,我们要么保持不动,要么前一天持有股票并在第 i 天卖出,取两者利润的最大值。
dp[i - 1][1]表示第 i - 1 天持有股票时的最大利润,即前一天的利润。dp[i - 1][0] + prices[i]表示前一天不持有股票时的最大利润加上第 i 天股票价格后的值,即前一天不持有股票,然后在第 i 天买入股票得到的利润。
因此,max(dp[i - 1][1], dp[i - 1][0] + prices[i]) 取了这两者之间的较大值,即在第 i 天持有股票时,我们要么保持不动,要么前一天不持有股票并在第 i 天买入,取两者利润的最大值。
代码:
class Solution {
public:// 计算股票的最大利润int maxProfit(vector<int>& prices) {int len = prices.size(); // 获取股票价格列表的长度vector<vector<int>> dp(len, vector<int>(2, 0)); // 定义二维动态规划数组dp,初始化为0dp[0][0] -= prices[0]; // 第一天持有股票的利润为 -prices[0]dp[0][1] = 0; // 第一天不持有股票的利润为0for (int i = 1; i < len; i++) {// 不持有股票的利润为前一天不持有股票的利润与前一天持有股票今天买入的利润的较大值dp[i][0] = max(dp[i - 1][0], dp[i - 1][1] - prices[i]); // 注意这里是和 买卖股票的最佳时机唯一不同的地方。// 持有股票的利润为前一天持有股票的利润与今天卖出股票的利润的较大值dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] + prices[i]);}return dp[len - 1][1]; // 返回最后一天不持有股票获得的利润}
};3买卖股票的最佳时机 III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:prices = [1,2,3,4,5] 输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。 因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4:
输入:prices = [1] 输出:0
提示:
1 <= prices.length <= 1050 <= prices[i] <= 105
3买卖股票的最佳时机 III
给定一个数组,它的第 i 个元素是一支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 两笔 交易。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:prices = [3,3,5,0,0,3,1,4] 输出:6 解释:在第 4 天(股票价格 = 0)的时候买入,在第 6 天(股票价格 = 3)的时候卖出,这笔交易所能获得利润 = 3-0 = 3 。随后,在第 7 天(股票价格 = 1)的时候买入,在第 8 天 (股票价格 = 4)的时候卖出,这笔交易所能获得利润 = 4-1 = 3 。
示例 2:
输入:prices = [1,2,3,4,5] 输出:4 解释:在第 1 天(股票价格 = 1)的时候买入,在第 5 天 (股票价格 = 5)的时候卖出, 这笔交易所能获得利润 = 5-1 = 4 。 注意你不能在第 1 天和第 2 天接连购买股票,之后再将它们卖出。 因为这样属于同时参与了多笔交易,你必须在再次购买前出售掉之前的股票。
示例 3:
输入:prices = [7,6,4,3,1] 输出:0 解释:在这个情况下, 没有交易完成, 所以最大利润为 0。
示例 4:
输入:prices = [1] 输出:0
提示:
1 <= prices.length <= 1050 <= prices[i] <= 105
思路:
-
定义动态规划数组: 我们首先定义一个二维数组
dp,其中dp[i][j]表示在第i天结束时进行第j次交易后的剩余最大现金。这里j取值范围为0到4,分别代表不进行交易、进行一次买入、进行一次卖出、进行两次买入、进行两次卖出。 -
初始化动态规划数组: 对于第一天,我们需要考虑可以进行的交易操作。因为题目要求最多可以完成两笔交易,所以第一天可以进行第一次买入和第二次买入。因此,我们将
dp[0][1]和dp[0][3]设置为负的第一天股票价格,表示在第一天结束时进行第一次买入和第二次买入操作后的剩余最大现金。 -
状态转移方程: 接下来,我们需要根据状态转移方程更新动态规划数组。具体地:
-
对于进行买入操作的情况,我们需要考虑前一天是否已经进行了相应的交易。根据状态转移方程,我们取前一天结束时未进行买入操作和前一天结束时已经进行了买入操作但保持不变或者在当天买入的较大值。
-
对于进行卖出操作的情况,同样需要考虑前一天是否已经进行了相应的交易。根据状态转移方程,我们取前一天结束时未进行卖出操作和前一天结束时已经进行了卖出操作但保持不变或者在当天卖出的较大值。
-
-
返回结果: 最后,我们返回
dp[prices.size() - 1][4],表示第len - 1天结束时进行第二次卖出操作后的剩余最大现金,即为问题的解。
代码:
class Solution {
public:
int maxProfit(vector<int>& prices) {
if (prices.size() == 0) return 0; // 如果股票价格列表为空,则返回0
vector<vector<int>> dp(prices.size(), vector<int>(5, 0)); // 定义二维动态规划数组dp,行数为股票价格列表的长度,列数为5,初始化为0
dp[0][1] = -prices[0]; // 第一天结束时进行第一次买入操作后的剩余最大现金为负的第一天股票价格
dp[0][3] = -prices[0]; // 第一天结束时进行第二次买入操作后的剩余最大现金为负的第一天股票价格
for (int i = 1; i < prices.size(); i++) {
// 计算第一次买入操作后的剩余最大现金
dp[i][0] = dp[i - 1][0];
dp[i][1] = max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
// 计算第一次卖出操作后的剩余最大现金
dp[i][2] = max(dp[i - 1][2], dp[i - 1][1] + prices[i]);
// 计算第二次买入操作后的剩余最大现金
dp[i][3] = max(dp[i - 1][3], dp[i - 1][2] - prices[i]);
// 计算第二次卖出操作后的剩余最大现金
dp[i][4] = max(dp[i - 1][4], dp[i - 1][3] + prices[i]);
}
return dp[prices.size() - 1][4]; // 返回第 len - 1 天结束时进行第二次卖出操作后的剩余最大现金
}
};4买卖股票的最佳时机 IV
给你一个整数数组 prices 和一个整数 k ,其中 prices[i] 是某支给定的股票在第 i 天的价格。
设计一个算法来计算你所能获取的最大利润。你最多可以完成 k 笔交易。也就是说,你最多可以买 k 次,卖 k 次。
注意:你不能同时参与多笔交易(你必须在再次购买前出售掉之前的股票)。
示例 1:
输入:k = 2, prices = [2,4,1] 输出:2 解释:在第 1 天 (股票价格 = 2) 的时候买入,在第 2 天 (股票价格 = 4) 的时候卖出,这笔交易所能获得利润 = 4-2 = 2 。
示例 2:
输入:k = 2, prices = [3,2,6,5,0,3] 输出:7 解释:在第 2 天 (股票价格 = 2) 的时候买入,在第 3 天 (股票价格 = 6) 的时候卖出, 这笔交易所能获得利润 = 6-2 = 4 。随后,在第 5 天 (股票价格 = 0) 的时候买入,在第 6 天 (股票价格 = 3) 的时候卖出, 这笔交易所能获得利润 = 3-0 = 3 。
提示:
1 <= k <= 1001 <= prices.length <= 10000 <= prices[i] <= 1000
思路:
-
边界情况处理:
- 首先检查股票价格数组是否为空,如果为空直接返回0。
-
初始化动态规划数组
dp:- 创建一个二维数组
dp,大小为prices.size() × (2 * k + 1),表示在不同天数和不同交易次数下的最大利润。
- 创建一个二维数组
-
第一天情况的初始化:
- 针对每次交易的买入操作,将
dp[0][j](奇数索引)设为-prices[0],表示第一次买入的情况。
- 针对每次交易的买入操作,将
-
动态规划状态转移:
- 从第二天开始遍历股票价格数组。
- 对于每天和每种交易次数,根据状态转移方程更新
dp[i][j]:dp[i][j + 1]:表示第j/2 + 1次买入股票的最大利润,可以选择继续保持不持有或者在前一天持有的基础上卖出。dp[i][j + 2]:表示第j/2 + 1次卖出股票的最大利润,可以选择继续持有或者在前一天未持有的基础上买入。
-
返回结果:
- 在所有交易完成后(即遍历完所有天数),返回
dp[prices.size() - 1][2 * k],表示在最后一天结束时,最多进行k次交易的最大利润。
- 在所有交易完成后(即遍历完所有天数),返回
代码:
class Solution {
public:int maxProfit(int k, vector<int>& prices) {// 边界情况处理:如果股票价格数组为空,直接返回0if (prices.size() == 0) return 0;// 初始化动态规划数组vector<vector<int>> dp(prices.size(), vector<int>(2 * k + 1, 0));// 初始化第一天的情况for (int j = 1; j < 2 * k; j += 2) {dp[0][j] = -prices[0]; // 第一次买入的情况}// 动态规划,根据状态转移方程更新dp数组for (int i = 1; i < prices.size(); ++i) {for (int j = 0; j < 2 * k - 1; j += 2) {// 第i天未持有股票的情况,考虑继续未持有或者在前一天持有的基础上卖出dp[i][j + 1] = max(dp[i - 1][j + 1], dp[i - 1][j] - prices[i]);// 第i天持有股票的情况,考虑继续持有或者在前一天未持有的基础上买入dp[i][j + 2] = max(dp[i - 1][j + 2], dp[i - 1][j + 1] + prices[i]);}}// 返回最后一天结束时,最多进行k次交易的最大利润return dp[prices.size() - 1][2 * k];}
};相关文章:
)
力扣练习题(2024/4/16)
1买卖股票的最佳时机 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔…...

c++中一些常用库函数
1.最大公约数 需要包括头文件#include<algorithm>,直接写__gcd(a,b),就是求a与b的最大公约数。 #include<iostream> #include<algorithm> #include<cstring> #include<cmath> #include<queue> #include<stack> #include<map>…...

竞赛 基于GRU的 电影评论情感分析 - python 深度学习 情感分类
文章目录 1 前言1.1 项目介绍 2 情感分类介绍3 数据集4 实现4.1 数据预处理4.2 构建网络4.3 训练模型4.4 模型评估4.5 模型预测 5 最后 1 前言 🔥 优质竞赛项目系列,今天要分享的是 基于GRU的 电影评论情感分析 该项目较为新颖,适合作为竞…...
软件杯 深度学习图像修复算法 - opencv python 机器视觉
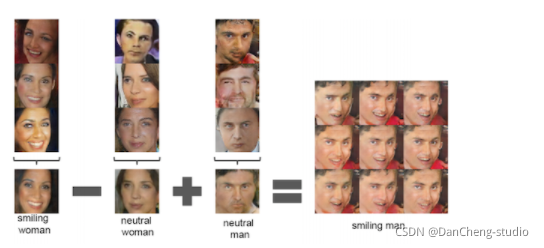
文章目录 0 前言2 什么是图像内容填充修复3 原理分析3.1 第一步:将图像理解为一个概率分布的样本3.2 补全图像 3.3 快速生成假图像3.4 生成对抗网络(Generative Adversarial Net, GAN) 的架构3.5 使用G(z)生成伪图像 4 在Tensorflow上构建DCGANs最后 0 前言 &#…...

java日志log4j使用
1、导入jar包 log4j-1.2.17.jar log4j-api-2.0-rc1.jar log4j-core-2.0-rc1.jar https://download.csdn.net/download/weixin_44201223/89148839 所需jar包下载地址 2、创建 log4j.properties src 下创建 log4j.properties (路径和名称都不允许改变),放置 src 下…...

探索Python爬虫利器:Scrapy框架解析与实战
探索Python爬虫利器:Scrapy框架解析与实战 在当今信息时代,数据的价值不言而喻。而Python爬虫技术,作为获取网络数据的重要手段,已经成为了许多数据分析师、开发者和研究者必备的技能。本文将为您详细介绍Python爬虫技术中的利器—…...
Rust腐蚀服务器修改背景和logo图片操作方法
Rust腐蚀服务器修改背景和logo图片操作方法 大家好我是艾西一个做服务器租用的网络架构师。在我们自己搭建的rust服务器游戏设定以及玩法都是完全按照自己的想法设定的,如果你是一个社区服那么对于进游戏的主页以及Logo肯定会有自己的想法。这个东西可以理解为做一…...

【架构-15】NoSQL数据库
NoSQL(Not Only SQL)数据库是一类非关系型数据库,与传统的关系型数据库(如MySQL、Oracle)相对而言。NoSQL数据库的设计目标是针对大规模数据和高并发访问的需求,具有高可扩展性、高性能和灵活的数据模型。 …...

中国人工智能产业年会智能交通与自动驾驶专题全景扫描
中国人工智能产业年会(CAIIAC)是中国人工智能技术发展和应用的重要展示平台,不仅关注创新,还涵盖了市场和监管方面的内容,对于促进人工智能领域的发展起到了重要作用。年会汇集了来自学术界、工业界和政府的专家&#…...
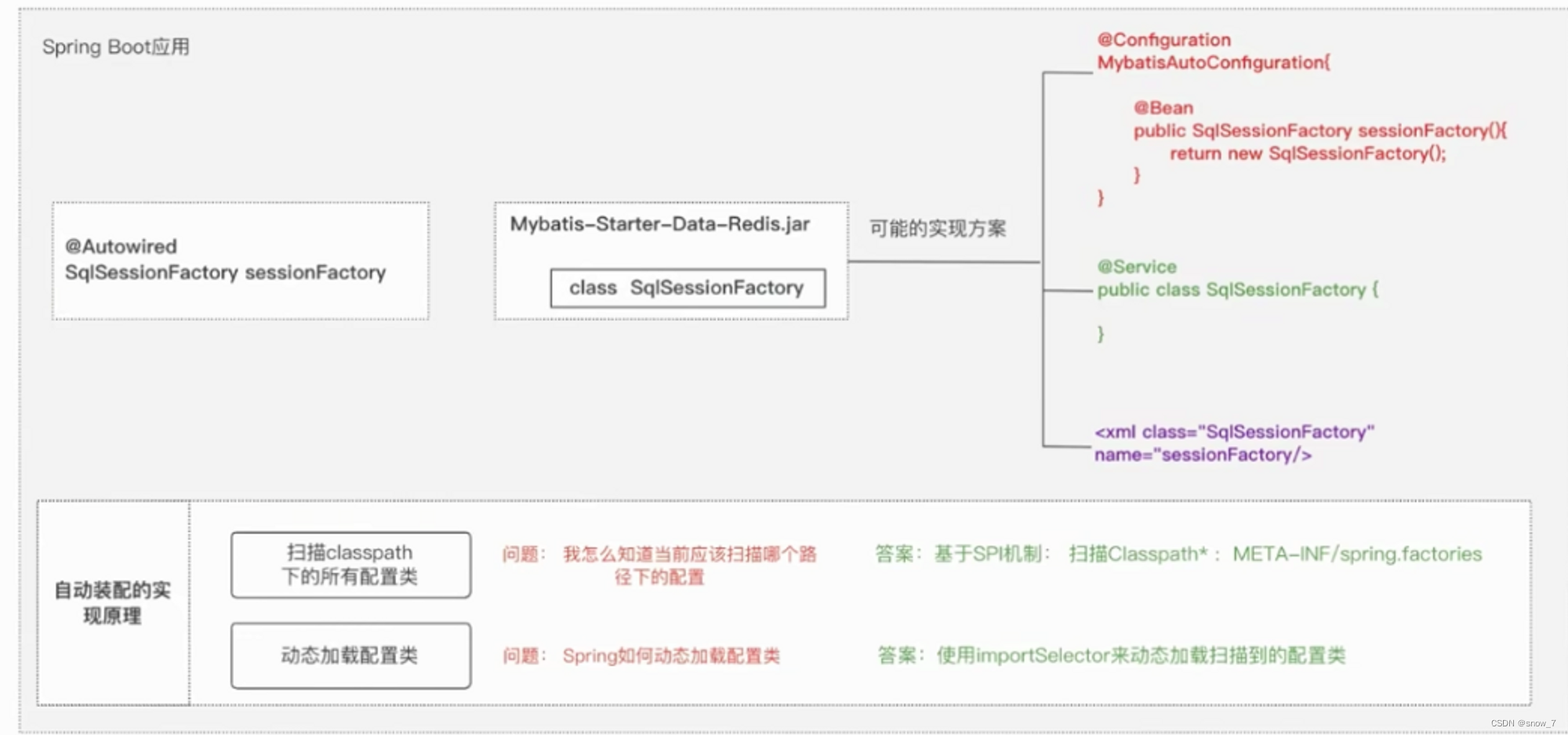
SpringBoot相关知识点总结
1 SpringBoot的目的 简化开发,开箱即用。 2 Spring Boot Starter Spring Boot Starter 是 Spring Boot 中的一个重要概念,它是一种提供依赖项的方式,可以帮助开发人员快速集成各种第三方库和框架。Spring Boot Starter 的目的是简化 Sprin…...
 clicked() clicked(bool)}达成巧用)
【QT】关于qcheckbox常用的三个信号,{sstateChanged(int) clicked() clicked(bool)}达成巧用
在 Qt 中,QCheckBox 是一个提供复选框功能的小部件,允许用户选择和取消选择一个或多个选项。QCheckBox 提供了几种信号来响应用户的交互,其中 stateChanged(int), clicked(), 和 clicked(bool) 是常用的。下面解释这些信号的意义及其用法。 …...
在线音乐网站的设计与实现
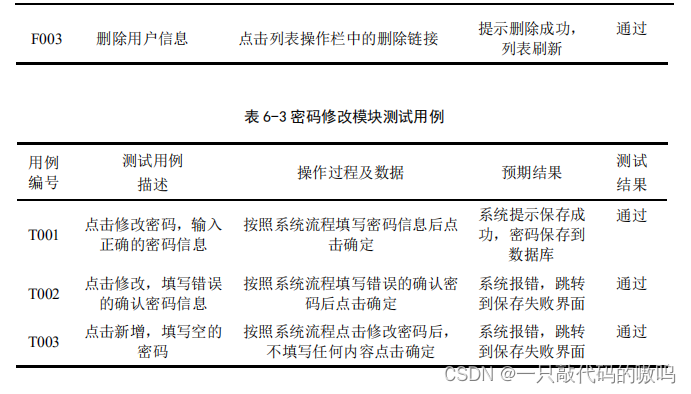
在线音乐网站的设计与实现 摘 要 在社会和互联网的快速发展中,音乐在人们生活中也产生着很大的作用。音乐可以使我们紧张的神经得到放松,有助于开启我们的智慧,可以辅助治疗,达到药物无法达到的效果,所以利用现代科学…...

【电路笔记】-数字缓冲器
数字缓冲器 文章目录 数字缓冲器1、概述2、单输入数字缓冲器3、三态缓冲器3.1 有效“高”三态缓冲器3.2 有效“高”反相三态缓冲器3.3 有效“低”三态缓冲器3.4 有效“低”反相三态缓冲器4、三态缓冲器控制数字缓冲器和三态缓冲器可以在数字电路中提供电流放大以驱动输出负载。…...

Opencv | 基于ndarray的基本操作
这里写目录标题 一. Opencv 基于ndarray的基本操作1. 浅拷贝2. np.copy ( ) 深拷贝3. 堆叠3.1 np.vstack ( ) 垂直方向堆叠3.2 np.hstack ( ) 水平方向堆叠 4. numpy创建图像5 np.transpose ( ) 更改维度顺序6. cv.resize ( ) 放大缩小7. np.clip ( ) 一. Opencv 基于ndarray的…...
【大语言模型】应用:10分钟实现搜索引擎
本文利用20Newsgroup这个数据集作为Corpus(语料库),用户可以通过搜索关键字来进行查询关联度最高的News,实现对文本的搜索引擎: 1. 导入数据集 from sklearn.datasets import fetch_20newsgroupsnewsgroups fetch_20newsgroups()print(fNu…...

UT单元测试
Tips:在使用时一定要注意版本适配性问题 一、Mockito 1.1 Mock的使用 Mock 的中文译为仿制的,模拟的,虚假的。对于测试框架来说,即构造出一个模拟/虚假的对象,使我们的测试能顺利进行下去。 Mock 测试就是在测试过程…...
leetcode-合并两个有序链表
目录 题目 图解 方法一 方法二 代码(解析在注释中) 方法一 编辑方法二 题目 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1: 输入:l1 [1,2,4], l2 [1,3,4] 输出:[1,1…...
006Node.js cnpm的安装
百度搜索 cnpm,进入npmmirror 镜像站https://npmmirror.com/ cmd窗口输入 npm install -g cnpm --registryhttps://registry.npmmirror.com...

web server apache tomcat11-01-官方文档入门介绍
前言 整理这个官方翻译的系列,原因是网上大部分的 tomcat 版本比较旧,此版本为 v11 最新的版本。 开源项目 同时也为从零手写实现 tomcat 提供一些基础和特性的思路。 minicat 别称【嗅虎】心有猛虎,轻嗅蔷薇。 系列文章 web server apac…...

java的总结
由于最近已经开始做项目了,所以对java的基础知识的学习都是一个离散化的状态没有一个很系统的学习,都是哪里不会就去学哪里。 先来讲一下前后端的区别吧 在我的理解前端就是:客户端在前端进行点击输入数据,前端将这些数据整合起来…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...
