每日OJ题_完全背包④_力扣279. 完全平方数(一维和二维)
目录
力扣279. 完全平方数
问题解析
解析代码
优化代码(相同子问题分析和滚动数组)
力扣279. 完全平方数
279. 完全平方数
难度 中等
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
示例 1:
输入:n = 12输出:3 解释:12 = 4 + 4 + 4
示例 2:
输入:n = 13输出:2 解释:13 = 4 + 9
提示:
1 <= n <= 10^4
class Solution {
public:int numSquares(int n) {}
};问题解析
(优化代码部分放了分析一维空间的思路,这个普通思路就简单描述了)
状态表示: dp[i][j] 表示:从前i个完全平方数中挑选,总和正好等于j,所有选法中最小的数量。
状态转移方程:
线性 dp 状态转移方程分析方式,一般都是根据最后一步的状况,来分情况讨论。但是最后一个物品能选很多个,因此需要分很多情况:
- 选 0 个i * i:dp[i][j] = dp[i - 1][j]
- 选 1 个i * i:dp[i][j] = dp[i - 1][j - i * i] + 1 ;
- 选 2 个i * i:dp[i][j] = dp[i - 1][j - 2 * i * i] + 2 ;
- ......
综上,状态转移方程为:
dp[i][j] = min(dp[i - 1][j] , dp[i - 1][j - i * i] + 1 + dp[i - 1][j - 2 * i * i] + 2 , ......)
这时发现,计算一个状态的时候,需要一个循环才能搞定的时候,我们要想到去优化。优化的方向就是用一个或者两个状态来表示这一堆的状态,通常就是用数学的方式做一下等价替换。
发现第二维是有规律的变化的,因此去看看 dp[i][j - i * i] + 1 ; 这个状态: dp[i][j - i * i] + 1 = min( dp[i - 1][j - 2 * i * i] + 2 , dp[i - 1][j - 3 * i * i] + 3 , ......)
因此可以修改我们的状态转移方程为: dp[i][j] = min(dp[i - 1][j] , dp[i][j - i * i] + 1。(j >= i * i )。有个技巧,就是相当于把第二种情况 dp[i - 1][j - i * i] + 1 里面的 i - 1 变成 i 即可。
初始化: 初始化第一行即可,dp[0[0]为1,第一行后面初始化成无穷大。
填表顺序: 根据状态转移方程,仅需从上往下填表。
返回值: 根据状态表示,返回 dp[根号n][n] 。
解析代码
class Solution {
public:int change(int amount, vector<int>& coins) {int n = coins.size();vector<int> dp(amount + 1, 0); // 滚动数组优化dp[0] = 1;for(int i = 1; i <= n; ++i){for(int j = coins[i - 1]; j <= amount; ++j){dp[j] = dp[j] + dp[j - coins[i - 1]];}}return dp[amount];}
};优化代码(相同子问题分析和滚动数组)
先看能不能将问题转化成我们熟悉的题型。这里给出一个用拆分出相同子问题的方式,定义一个状态表示。(得到的结果 i 和 j 换一下就是滚动数组优化的结果)
为了叙述方便,把和为 n 的完全平方数的最少数量简称为最小数量。
对于 12 这个数,分析一下如何求它的最小数量。
- 如果 12 本身就是完全平方数,就不用算了,直接返回 1 ;
- 但是 12 不是完全平方数,试着把问题分解⼀下:
- 情况一:拆出来一个 1 ,然后看看 11 的最小数量,记为 x1 ;
- 情况二:拆出来一个 4 ,然后看看 8 的最小数量,记为 x2 ;(为什么拆出来 4 , 而不拆出来 2 呢?)
- 情况三:拆出来一个 8 ...... 其中,接下来求 11、8 的时候,其实又回到了原来的问题上。
因此,可以尝试用 dp 的策略,将 1 2 3 4 6 等等这些数的最小数量依次保存起来。再求较大的 n 的时候,直接查表,然后找出最小数量。
状态表示: dp[i] 表示:和为 i 的完全平方数的最少数量。
状态转移方程:
对于 dp[i] ,根据思路里的分析知道,可以根据小于等于 i 的所有完全平方数 x 进行划分:
- x = 1 时,最小数量为: 1 + dp[i - 1] ;
- x = 4 时,最小数量为: 1 + dp[i - 4] ......
为了方便枚举完全平方数,采用的策略: for(int j = 1; j * j <= i; j++)
综上,状态转移方程为:
dp[i] = min(dp[i], dp[i - j * j] + 1)
初始化:当 n = 0 的时候,没法拆分,结果为 0 ; 当 n = 1 的时候,结果为 1 。
填表顺序: 根据状态转移方程,仅需从左往右填表。
返回值: 根据状态表示,返回 dp[n] 。
class Solution {
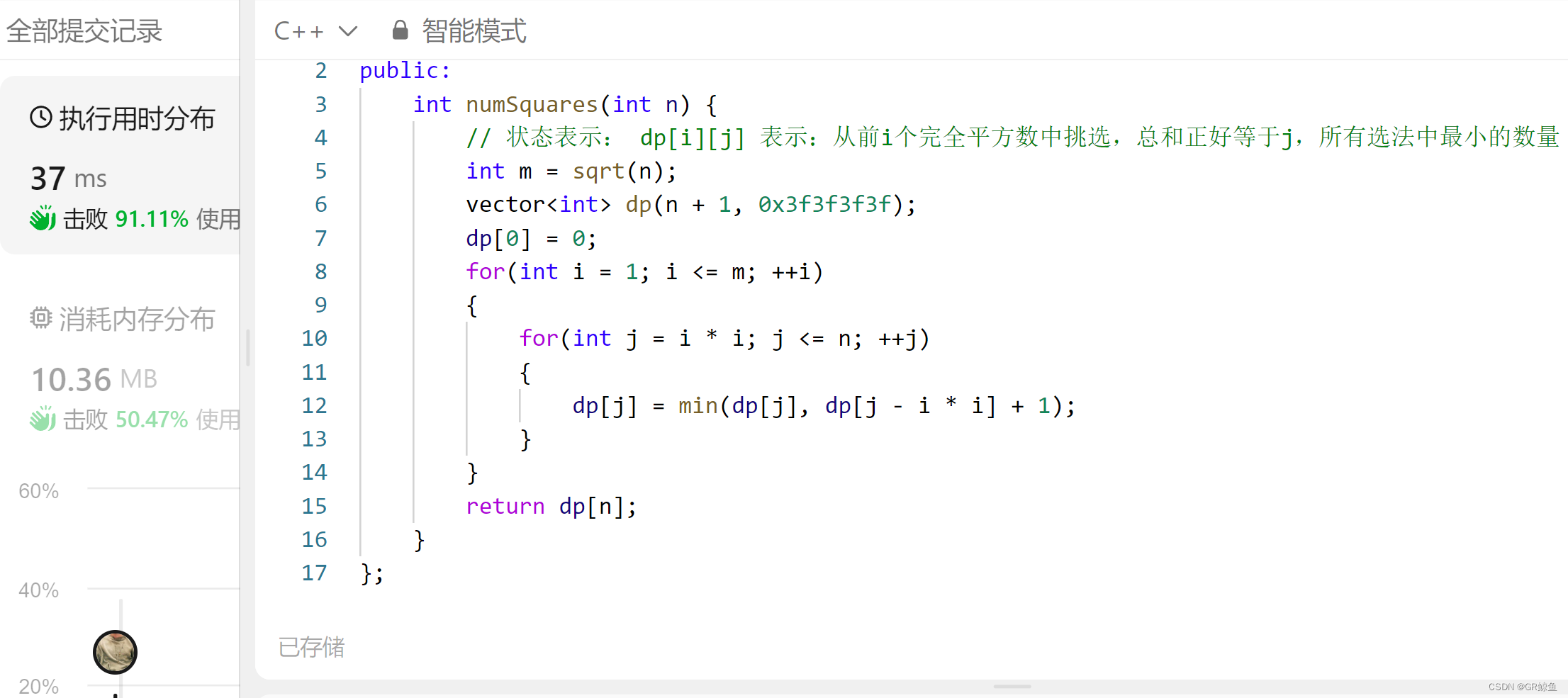
public:int numSquares(int n) {// dp[i] 表示:和为 i 的完全平方数的最少数量int m = sqrt(n);vector<int> dp(n + 1, 0x3f3f3f3f);dp[0] = 0;for(int i = 1; i <= m; ++i){for(int j = i * i; j <= n; ++j){dp[j] = min(dp[j], dp[j - i * i] + 1);}}return dp[n];}
};
相关文章:

每日OJ题_完全背包④_力扣279. 完全平方数(一维和二维)
目录 力扣279. 完全平方数 问题解析 解析代码 优化代码(相同子问题分析和滚动数组) 力扣279. 完全平方数 279. 完全平方数 难度 中等 给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。 完全平方数 是一个整数,其值…...
web项目中jsp页面不识别el表达式
如果使用el表达式出现下图问题 ** 解决办法 ** 这是因为maven创建项目时,web.xml头部声明默认是2.3,这个默认jsp关闭el表达式 修改web.xml文件开头的web-app的版本 <?xml version"1.0" encoding"UTF-8"?> <web-app x…...

【Python基础】字典
文章目录 [toc]什么是字典键值对示例键异常 遍历列表什么是遍历遍历字典的键keys()方法 遍历字典的值values()方法 遍历字典的键值对items()方法 字典操作增加键值对修改键值对查询键值对get()方法 删除键值对delclear()方法 个人主页:丷从心 系列专栏:…...
2024HW --> 安全产品 Powershell无文件落地攻击
在HW中,除了了解中间件,web漏洞,这些攻击的手法,还得了解应急响应,安全产品,入侵排查,溯源反制...... 那么今天,就来说一下安全产品(安全公司我就不说了,这个…...

力扣哈哈哈哈
public class MyStack {int top;Queue<Integer> q1;Queue<Integer> q2;public MyStack() {q1new LinkedList<Integer>();q2new LinkedList<Integer>();}public void push(int x) {q2.offer(x);//offer是入队方法while (!q1.isEmpty()){q2.offer(q1.pol…...
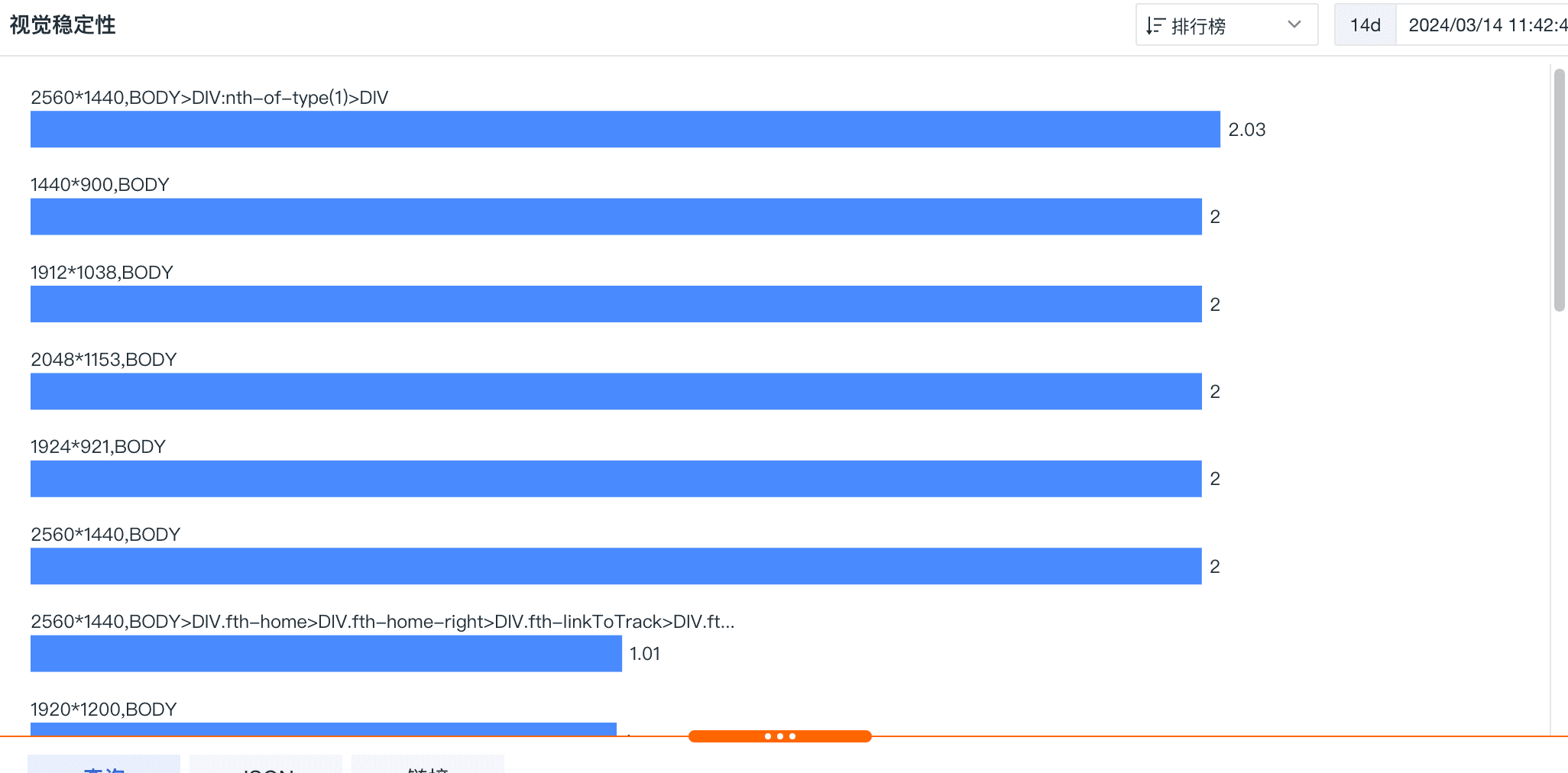
RUM 最佳实践-视觉稳定性的探索与实践
写在前面的话 在当今数字时代,网页的视觉稳定性对于提供良好的用户体验至关重要。其中一个衡量视觉稳定性的关键指标就是累积布局偏移(Cumulative Layout Shift,简称 CLS)。CLS 作为 Web Vitals 指标之一,它衡量的是网…...
PostgreSQL的学习心得和知识总结(一百三十八)|深入理解PostgreSQL数据库之Protocol message构造和解析逻辑
目录结构 注:提前言明 本文借鉴了以下博主、书籍或网站的内容,其列表如下: 1、参考书籍:《PostgreSQL数据库内核分析》 2、参考书籍:《数据库事务处理的艺术:事务管理与并发控制》 3、PostgreSQL数据库仓库…...

爬虫开发教程
一、爬虫概述 爬虫(也称为网络爬虫或蜘蛛)是一种自动化程序,能够模拟人类在互联网上浏览和抓取数据的行为。它通过发送HTTP请求,获取网页的HTML代码,然后解析这些代码以提取有用的数据。爬虫在数据分析、价格监测、竞…...
【Python】高级进阶(专版提升3)
Python 1 程序结构1.1 模块 Module1.1.1 定义1.1.2 作用1.1.3 导入1.1.3.1 import1.1.3.2 from import 1.1.4 模块变量1.1.5 加载过程1.1.6 分类 1.2 包package1.2.1 定义1.2.2 作用1.2.3 导入1.1.3.1 import1.1.3.2 from import 2 异常处理Error2.1 异常2.2 处理 3 迭代3.1 可…...

LeetCode 1378、1277、2944
1378 二级排序,compare函数必须是static的 class Solution { public:struct node {int val;int priority;};static bool compare(const node &n1, const node &n2) {if (n1.priority n2.priority) {return n1.val < n2.val;}return n1.priority < n…...
【缓存常见问题】
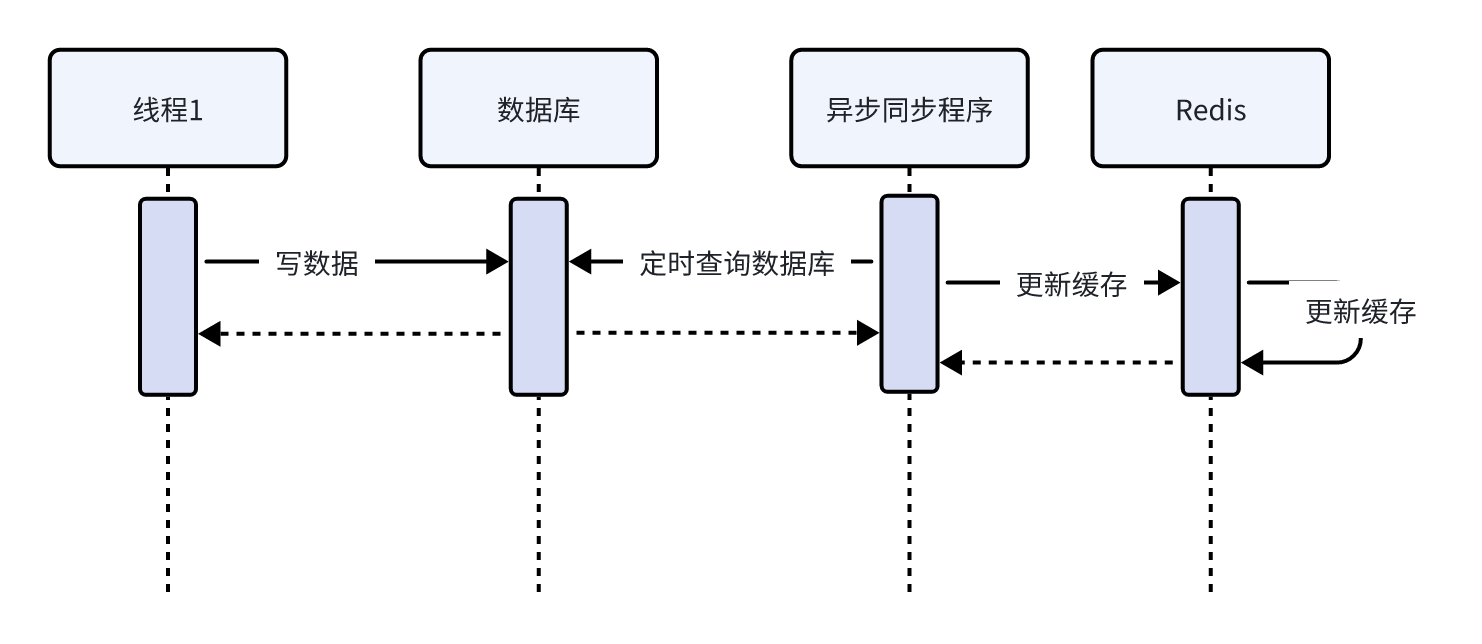
在使用缓存时特别是在高并发场景下会遇到很多问题,常用的问题有缓存穿透、缓存击穿、缓存雪崩以及缓存一致性问题。 1、缓存穿透 首先,什么是缓存穿透呢? 缓存穿透是指请求一个不存在的数据,缓存层和数据库层都没有这个数据&…...

Python爬取猫眼电影票房 + 数据可视化
目录 主角查看与分析 爬取可视化分析猫眼电影上座率前10分析猫眼电影票房场均人次前10分析猫眼电影票票房占比分析 主角查看与分析 爬取 对猫眼电影票房进行爬取,首先我们打开猫眼 接着我们想要进行数据抓包,就要看网站的具体内容,通过按F12…...

Spring Boot深度解析:是什么、为何使用及其优势所在
在Java企业级应用开发的漫长历史中,Spring框架以其卓越的依赖注入和面向切面编程的能力,赢得了广大开发者的青睐。然而,随着技术的不断进步和项目的日益复杂,传统的Spring应用开发流程逐渐显得繁琐和低效。为了解决这一问题&#…...

面向对象——类与对象
文章目录 类与对象构造函数、析构函数get/set方法函数:类内声明、类外定义static 类与对象 #include<iostream> #include<string> using namespace std; /* 类与对象 */ class Person{public:string name;// 固有属性,成员变量 int age;pu…...

Golang的[]interface{}为什么不能接收[]int?
在 Go 中,[]interface{} 和 []int 是两种不同的类型,虽然它们的底层数据结构都是切片,但是它们的元素类型不同。[]interface{} 是一个空接口切片,可以容纳任意类型的元素,而 []int 是一个整数切片,只能容纳…...
重启服务器或重启docker,导致emqx的Dashboard的密码重置为public
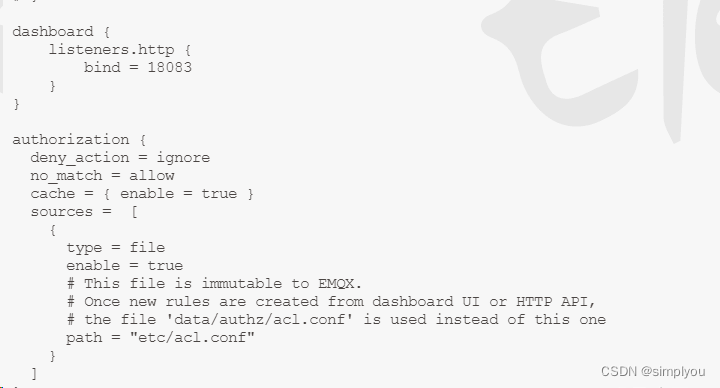
最近在项目中突然发现重启服务器,或者重启docker 修改好的emqx的Dashboard的密码重置为public 技术博客 http://idea.coderyj.com/ 1.解决办法就是固定 emqx的节点 # 拉取镜像 docker pull emqx/emqx# 创建目录,进行目录挂载 mkdir -p /docker/emqx/{etc,lib,data,…...

就业班 第三阶段(ansible) 2401--4.16 day2 ansible2 剧本+角色
六、Ansible playbook 简介 playbook 是 ansible 用于配置,部署,和管理被控节点的剧本。 通过 playbook 的详细描述,执行其中的一系列 tasks ,可以让远端主机达到预期的状态。playbook 就像 Ansible 控制器给被控节点列出的的…...

常用的过滤网站扫描网站攻击的路径是那些,比如:/etc/passwd等
网站攻击中经常被尝试的路径主要包括利用漏洞获取敏感文件、执行系统命令或者注入恶意代码的尝试。以下是一些常见的被攻击者尝试访问的路径和文件,这些通常在网络入侵检测系统(IDS)和网络防火墙的过滤规则中被特别关注: 系统文件…...
考研数学|《1800》《660》《880》如何选择和搭配?(附资料分享)
直接说结论:基础不好先做1800、强化之前660,强化可选880/1000题。 首先,传统习题册存在的一个问题是题量较大,但难度波动较大。《汤家凤1800》和《张宇1000》题量庞大,但有些题目难度不够平衡,有些过于简单…...

论文笔记:Are Human-generated Demonstrations Necessary for In-context Learning?
iclr 2024 reviewer 评分 6668 1 intro 大型语言模型(LLMs)已显示出在上下文中学习的能力 给定几个带注释的示例作为演示,LLMs 能够为新的测试输入生成输出然而,现行的上下文学习(ICL)范式仍存在以下明显…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

macOS多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用
文章目录 问题现象问题原因解决办法 问题现象 macOS启动台(Launchpad)多出来了:Google云端硬盘、YouTube、表格、幻灯片、Gmail、Google文档等应用。 问题原因 很明显,都是Google家的办公全家桶。这些应用并不是通过独立安装的…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...
