StarryCoding入门教育赛2 题解 C++代码(推荐学习)
比赛地址:https://www.starrycoding.com/contest/6
比赛介绍
- 系列赛名称:StarryCoding 入门教育赛
- 难度:语法~较低
- 时长: 1.5 1.5 1.5小时
- 比赛时间:约每2-3天一场,一般为晚上18:30~20:00
- 赛后题解:赛后立即发布,包含文字题解
- Rating结算范围: < 3000 < 3000 <3000
面向群体
- 有学习过程序设计课程,希望提高自己的编程水平、思维能力、算法能力的同学。
- 准备参加各种程序设计、算法竞赛(例如ACM、蓝桥杯、GPLT天梯赛等)的同学。
- 希望通过保/考研的机试、就业的算法笔/面试的同学。
- 非计算机专业,但对编程/算法感兴趣的同学。
- 想要感受编程竞赛的计算机专业新生同学。
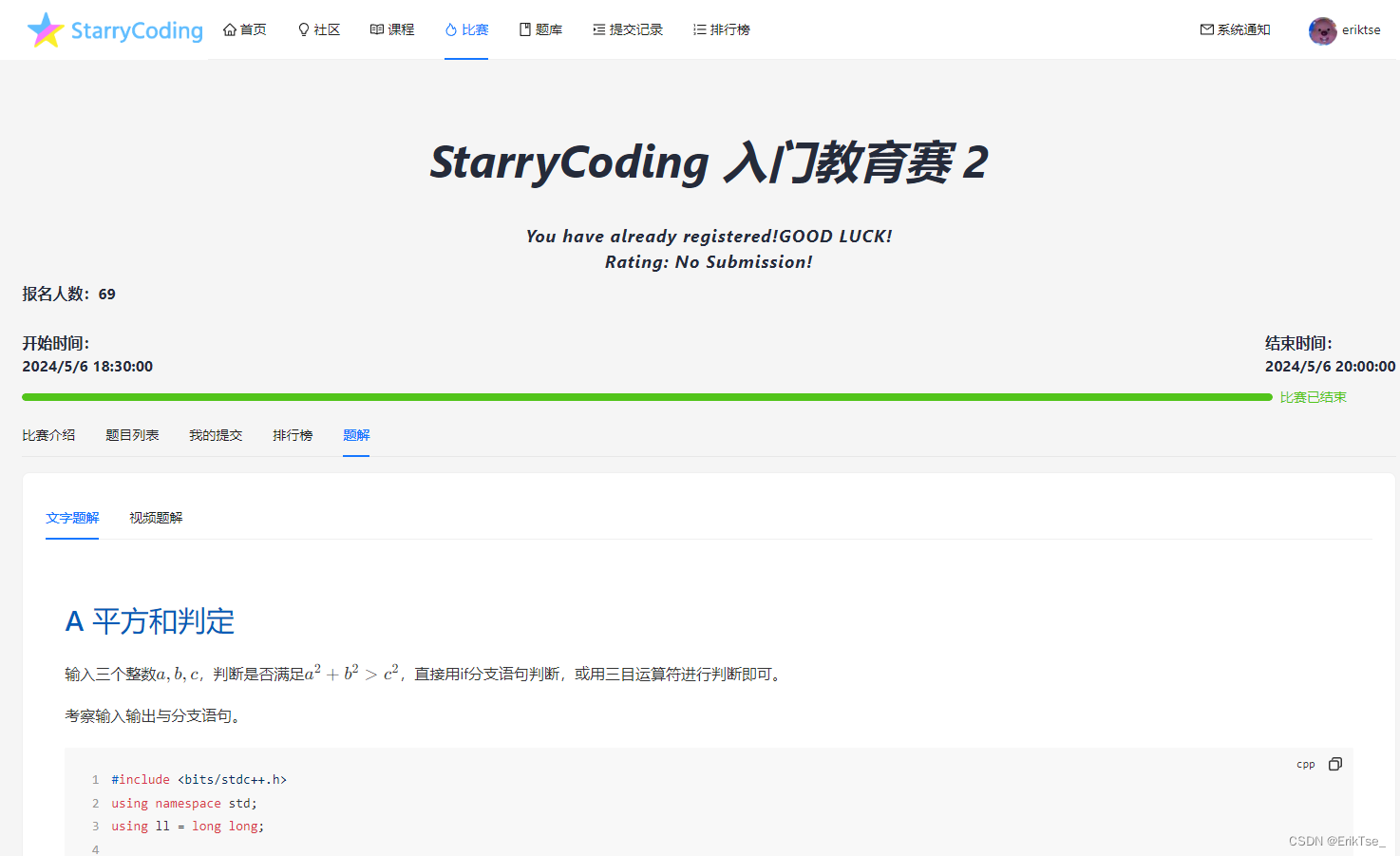
A 平方和判定
输入三个整数 a , b , c a, b, c a,b,c,判断是否满足 a 2 + b 2 > c 2 a^2 + b^2 > c^2 a2+b2>c2,直接用if分支语句判断,或用三目运算符进行判断即可。
考察输入输出与分支语句。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;void solve()
{ll a, b, c;cin >> a >> b >> c;cout << (a * a + b * b > c * c ? "YES" : "NO") << '\n';
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _;cin >> _;while (_--)solve();return 0;
}
B 矩阵判定
枚举四元组 ( i 1 , j 1 , i 2 , j 2 ) (i_1, j_1, i_2, j_2) (i1,j1,i2,j2),判断对于所有四元组是否满足 A i 1 , j 1 + A i 2 , j 2 > A i 2 , j 1 + A i 1 , j 2 A_{i_1, j_1}+A_{i_2,j_2} > A_{i_2,j_1}+A_{i_1, j_2} Ai1,j1+Ai2,j2>Ai2,j1+Ai1,j2即可。
时间复杂度为 O ( n 2 m 2 ) O(n^2m^2) O(n2m2)。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 53;
ll a[N][N];
void solve()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; ++i)for (int j = 1; j <= m; ++j)cin >> a[i][j];for (int i = 1; i <= n; ++i){ // i1for (int j = i + 1; j <= n; ++j){ // i2for (int k = 1; k <= m; ++k){ // j1for (int l = k + 1; l <= m; ++l){ // j2if (a[i][k] + a[j][l] <= a[i][l] + a[j][k]){cout << "NO\n";return;}}}}}cout << "YES\n";
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _;cin >> _;while (_--)solve();return 0;
}
C 曼哈顿种类
枚举所有点对,计算其曼哈顿距离后放入 s e t set set中计算 s i z e size size,或放入数组中排序去重。
#include <bits/stdc++.h>
using namespace std;
using ll = long long;const int N = 1e3 + 9;ll x[N], y[N];ll getabs(ll x) { return x < 0 ? -x : x; }void solve()
{int n;cin >> n;for (int i = 1; i <= n; ++i)cin >> x[i] >> y[i];set<ll> st;for (int i = 1; i <= n; ++i)for (int j = i + 1; j <= n; ++j){st.insert(getabs(x[i] - x[j]) + getabs(y[i] - y[j]));}cout << st.size() << '\n';
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _;cin >> _;while (_--)solve();return 0;
}
D 小e消消乐
根据题意,我们要联想到“栈”这个数据结构,并且注意题目中的弹珠大小不是 A i A_i Ai,而是 2 A i 2^{A_i} 2Ai哟,所以两个大小相等的弹珠合并,相当于把指数(也就是 A i A_i Ai)增加 1 1 1,而不是翻倍哦。
一些细节需要考虑,例如用while而不是if、栈内元素数量得大于 2 2 2才能合并等等。
#include <bits/stdc++.h>
using namespace std;using ll = long long;
const ll N = 1e5 +9;
ll a[N];int main()
{int n; cin >> n;int cnt = 0;for (int i = 1; i <= n; ++ i){cin >> a[++ cnt];while(cnt >= 2 && a[cnt] == a[cnt - 1])a[-- cnt]++;}cout << cnt << '\n';return 0;
}
E 妹妹太多怎么办呐!
首先通过数据范围猜测,可以接受时间复杂度 O ( n ! ) O(n!) O(n!)的做法,于是大胆去想 d f s dfs dfs。
对于一种方案,实际上是一种“坐标的排列”,只要坐标排列确定了,那么最终的愉悦度也确定了,于是可以通过 d f s dfs dfs枚举所有的方案,对于每种方案计算结果取最大即可。
这里需要注意的细节是,愉悦度不是单调的,有可能为负数。
如果对dfs深度优先搜索算法不熟悉的同学,推荐先看一下《算法基础课》https://www.starrycoding.com/course/1
#include <bits/stdc++.h>
using namespace std;
using ll = long long;const int N = 20;ll x[N], y[N], a[N];ll getabs(ll x) { return x < 0 ? -x : x; }ll dist(ll u, ll v)
{return getabs(x[u] - x[v]) + getabs(y[u] - y[v]);
}bitset<12> vis;
int n, k;
ll ans, asum;
int f[N]; // 表示选出的排列
// dep是层数,sum是当前的愉悦度
void dfs(int dep, ll sum)
{if(sum + asum <= ans)return;// 递归出口if (dep == k + 1){ans = max(ans, sum);return;}for (int i = 1; i <= n; ++i){// 已经去过了if (vis[i])continue;f[dep] = i;vis[i] = true;dfs(dep + 1, sum + a[i] - dist(f[dep - 1], i));vis[i] = false;}
}void solve()
{cin >> n >> k;for (int i = 1; i <= n; ++i)cin >> x[i] >> y[i] >> a[i];asum = 0;for(int i = 1;i <= n; ++ i)asum += a[i];ans = -2e18;vis.reset();dfs(1, 0);cout << ans << '\n';
}int main()
{ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);int _;cin >> _;while (_--)solve();return 0;
}
相关文章:

StarryCoding入门教育赛2 题解 C++代码(推荐学习)
比赛地址:https://www.starrycoding.com/contest/6 比赛介绍 系列赛名称:StarryCoding 入门教育赛难度:语法~较低时长: 1.5 1.5 1.5小时比赛时间:约每2-3天一场,一般为晚上18:30~20:00赛后题解࿱…...

【JAVA进阶篇教学】第九篇:MyBatis-Plus用法介绍
博主打算从0-1讲解下java进阶篇教学,今天教学第九篇:MyBatis-Plus用法介绍。 在 MyBatis-Plus 3.5.0 中,LambdaQueryWrapper支持多种条件构造方式,除了等于(eq)、不等于(ne)、大于&a…...

实时音视频通信的主要矛盾及解决方法
实时音视频通信的主要矛盾及解决方法 实时音视频通信的主要矛盾及解决方法实时音视频通信的主要矛盾矛盾的解决方法增加带宽减少数据量适当增加延时提高网络质量快速准确地评估带宽 总结参考 实时音视频通信的主要矛盾及解决方法 实时音视频通信的主要矛盾 实时音视频通信的主…...

【Delphi 爬虫库 4】使用封装好的 XML 解析库对 XML 数据进行解析
由于官方提供的TXMLDocument组件并不是特别好用,有着体积大,速度慢,调用不方便等缺点。 这里直接利用封装好的XML 解析库来对Xml数据进行解析与生成。 文章目录 1、生成XML文件2、解析XML文件3、生成带注释的XML文件4、删除XML文件节点 1、生…...
Flask简介
Flask简介 安装概述使用PyCharm创建一个Flask程序 Flask程序的基本结构初始化路由和视图函数启动服务器请求-响应循环 安装 概述 Flask算是小型框架,小到可以称为“微框架”。Flask 非常小,因此你一旦能够熟练使用它,很可能就能读懂它所有的…...
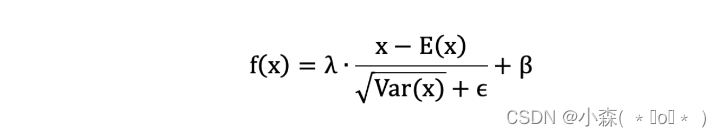
神经网络中的归一化
我们今天介绍一下神经网络中的归一化方法~ 之前学到的机器学习中的归一化是将数据缩放到特定范围内,以消除不同特征之间的量纲和取值范围差异。通过将原始数据缩放到一个特定的范围内,比如[0,1]或者[-1,1],来消除不同特征之间的量纲和取值范围…...

《从Paxos到Zookeeper》——第四、七章:基本概念及原理
目录 第四章 Zookeeper与Paxos 4.1 Zk是什么 4.1.1 Zk特性 4.1.2 Zk基本概念 4.1.2.1 集群角色(Follower, Leader, Observer) 4.1.2.2 数据模型 4.1.2.3 ZNode(数据节点) 4.1.2.4 Session(会话) 4.1.2.5 ACL(Access Control Lists) 4.1.2.6 Watcher(事件…...
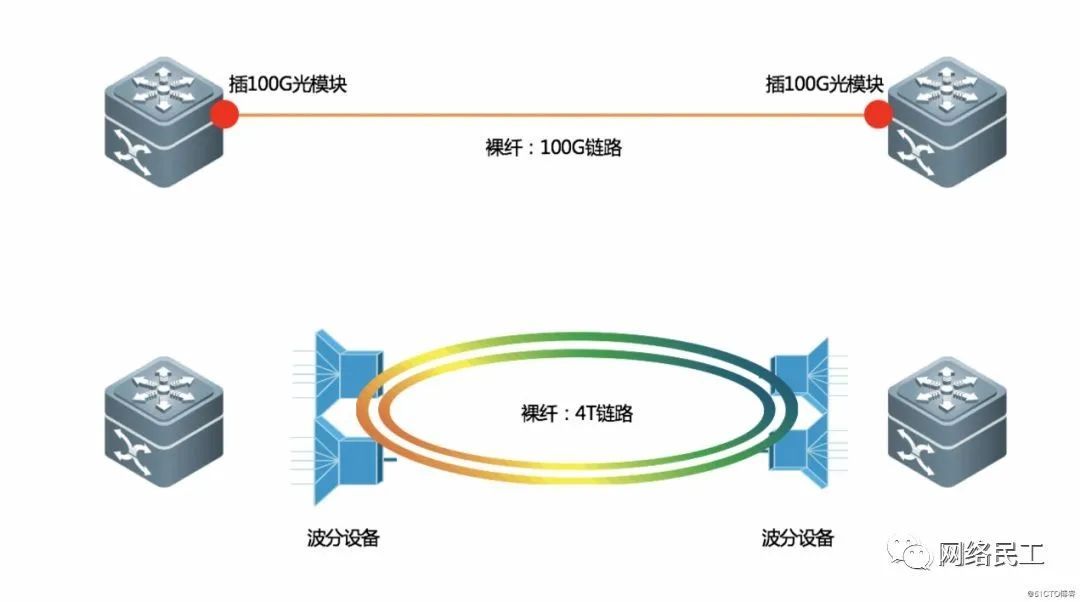
网络演进技术演进:裸纤专线、SDH、MSTP+、OTN、PTN、IP-RAN
前言 文章主要介绍常见名词以及其在各自领域实现的功能价值。 01 裸纤 裸光纤(裸光纤)由运营商提供,是无中继的光纤线路,仅通过配线架连接。相比传统光纤,裸光纤提供纯粹的物理传输路径,无需额外网…...

MMC设备
MMC(MultiMediaCard)是一种闪存卡标准,用于作为便携式设备上的存储媒介,例如数码相机、智能手机、平板电脑、个人数字助理(PDA)以及其他便携式设备。MMC卡最初是由SanDisk和Siemens AG开发的,并…...

图片浏览器-PicView
一、前言 PicView 是一款适用于 Windows 10 或 11 的快速高效的图像查看器,配备了干净简洁的用户界面,可以在不需要时方便地隐藏。 二、支持类型 它支持广泛的图像文件类型,包括:WEBP、GIF、SVG、PNG、JXL、HEIC、PSD 三、软件特…...

一些零碎小知识
函数递归复习 #define 的头文件包含 #define定义标识符常量 等define其他用法 斐波那契数列 函数栈帧 青蛙跳台问题 汉诺塔问题 字符“0”与0的计算 “0”-“0”0; 最后一次作业题一道 素数 随机数 strand timer rand 水仙花数 变种随鲜花 斐波那契数…...
2.2 Java全栈开发前端+后端(全栈工程师进阶之路)-前端框架VUE3-基础-Vue基本语法
文本渲染指令 文本渲染指令-v-html与v-text Vue使用了基于HTML的模板语法,允许开发者声明式地将DOM绑定至底层Vue实例的数据。所有Vue的模板都是 合法的HTML,所以能被遵循规范的浏览器和HTML解析器解析。 在前面,我们一直使用的是字符串插…...
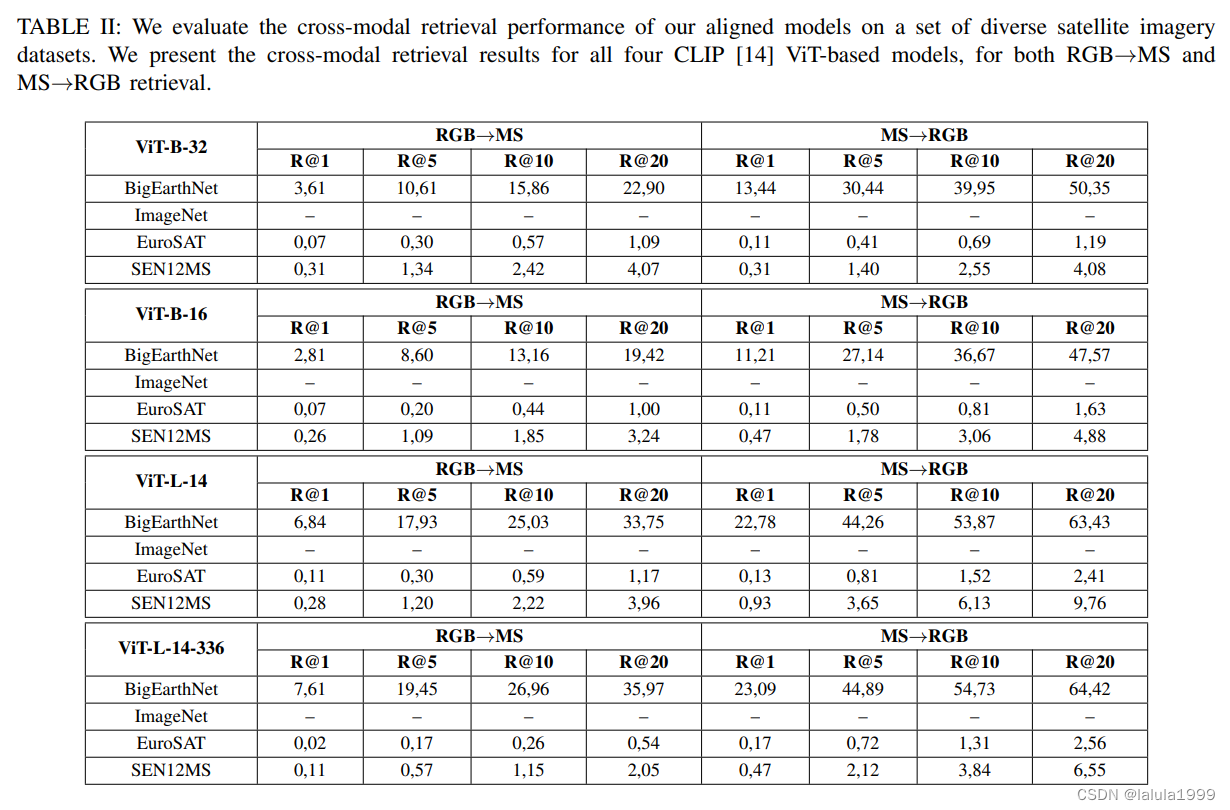
(Arxiv,2024)Mind the Modality Gap:通过跨模态对齐建立遥感视觉语言模型
文章目录 相关资料摘要引言相关工作对比语言图像预训练遥感域专用 CLIP 模型遥感中的多模态 CLIP 启发模型 方法模型算法输入阶段:输出阶段:步骤说明: 第一阶段:通过权重插值修补CLIP将遥感图像模态与自然图像和文本对齐 实验 相关…...
)
区块链 | 一文了解 NFT 的生态系统(上)
🐶原文: Understanding Security Issues in the NFT Ecosystem 🐶写在前面: 本博客只摘取了原论文的第二、三节。 技术背景知识 在本节中,我们将介绍以太坊生态系统的构建模块,重点关注「NFT,…...

为什么centos官方版不支持arm架构?
为什么centos官方版不支持arm架构? 1、资源限制:CentOS是由社区维护的开源操作系统,其开发和维护需要大量的人力和物力资源。由于ARM架构的设备相对较少,社区资源有限,因此官方版CentOS选择集中精力在x86架构上进行开发…...
)
awk小尝试2(随手记)
文章目录 需求1解法 需求2解法(3种-grep/sed/awk) 需求1 使用hostname -I创建文件名 echo hostname -I.txt 10.0.0.124 .txt # 需要注意,这里的.txt前有一个空格,需要去掉,不然就是两个文件名解法 echo hostname -I…...
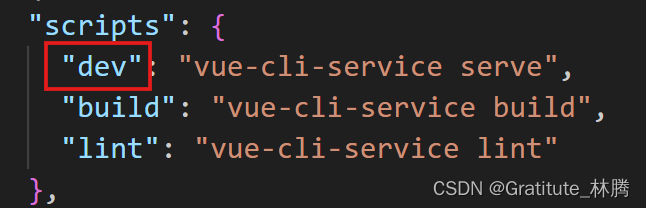
Vue的项目启动指令分析
通过Vue CLI脚手架创建的项目,默认的启动项目方式是 npm run serve 这里的serve是可以修改的。 在创建的项目目录中,找到package.json 双击打开,找到scripts部分 在scripts部分,有一个"serve"键值对,这里的…...

年轻人刮疯了,刮刮乐断货了
年轻人刮疯了 刮刮乐缺货了。 00后彩票店老板陆诗等得有点着急。她的福彩店开在深圳,今年4月才开门营业,但从开业到今天,刮刮乐总共就来了一回货——开业时发的20本。 那之后,刮刮乐就彻底断供了。原本,陆诗想把刮刮…...

25 JavaScript学习:var let const
JavaScript全局变量 JavaScript中全局变量存在多种情况和定义方式,下面详细解释并提供相应的举例: 使用var关键字声明的全局变量: var globalVar "我是全局变量";未使用var关键字声明的变量会成为全局变量(不推荐使用&…...
docker部署的nacos2.2x开启鉴权功能
注意在2.2.0版本之后如果不开启鉴权,那么默认不需要登录就可以访问 所以我们需要手动开启鉴权,nacos启动好以后来到容器内部修改 docker exec -it nacos /bin/shvim conf/application.properties在第34行下面添加 nacos.core.auth.enabledtrue nacos.cor…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

【Oracle】分区表
个人主页:Guiat 归属专栏:Oracle 文章目录 1. 分区表基础概述1.1 分区表的概念与优势1.2 分区类型概览1.3 分区表的工作原理 2. 范围分区 (RANGE Partitioning)2.1 基础范围分区2.1.1 按日期范围分区2.1.2 按数值范围分区 2.2 间隔分区 (INTERVAL Partit…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

稳定币的深度剖析与展望
一、引言 在当今数字化浪潮席卷全球的时代,加密货币作为一种新兴的金融现象,正以前所未有的速度改变着我们对传统货币和金融体系的认知。然而,加密货币市场的高度波动性却成为了其广泛应用和普及的一大障碍。在这样的背景下,稳定…...
