算法提高之树的中心
算法提高之树的中心
-
核心思想:树形dp + 换根dp
-
每个点作为根节点 找其子树的最大距离和父节点的最大距离
-
dfs1:求子树对于当前根节点的最大距离和次大距离
- 求次大距离原因:如果当前节点是其父节点子树的最大路径上的点,最大距离不能用

-
dfs2:找父节点以上的最长距离
-
-
#include <iostream>#include <cstring>#include <algorithm>using namespace std;const int N = 10010,M=N<<1,INF=0x3f3f3f3f;int n;int h[N],e[M],ne[M],w[M],idx;int d1[N],d2[N],up[N];int s1[N],s2[N]; //s1存该点最大距离从哪个点过来 s2存次大距离...void add(int a, int b, int c){e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;}void dfs1(int u,int father){for(int i=h[u];~i;i=ne[i]){int j=e[i];if(j == father) continue;dfs1(j,u);if(d1[j] + w[i] >= d1[u]){d2[u] = d1[u],d1[u] = d1[j]+w[i];s2[u] = s1[u],s1[u] = j;}else if(d1[j] + w[i]> d2[u]){d2[u] = d1[j]+w[i] , s2[u] = j;}}}void dfs2(int u,int father){for(int i=h[u];~i;i=ne[i]){int j=e[i];if(j==father) continue;//如果j为求最大距离时用的点 d1[u]不能用if(s1[u] == j) up[j] = w[i] + max(up[u],d2[u]); else up[j] = w[i] + max(up[u],d1[u]);dfs2(j,u);}}int main(){memset(h,-1,sizeof h);cin>>n;for(int i=1;i<n;i++){int a,b,c;cin>>a>>b>>c;add(a,b,c) , add(b,a,c);}dfs1(1,-1);dfs2(1,-1);int res=INF;for(int i=1;i<=n;i++) res = min(res,max(d1[i],up[i]));cout<<res<<endl;}
相关文章:

算法提高之树的中心
算法提高之树的中心 核心思想:树形dp 换根dp 每个点作为根节点 找其子树的最大距离和父节点的最大距离 dfs1:求子树对于当前根节点的最大距离和次大距离 求次大距离原因:如果当前节点是其父节点子树的最大路径上的点,最大距离不…...
【Java基础】面向对象是什么
面向对象和面向过程的对比 类和对象 class Car{} 是描述对象(车)的类,属于引用数据类型用来描述对象具有的属性(变量)和行为(函数),属于概念模型 Car baomanew Car(); 对象需要由类来创建对象具备了类中定义的属性和行为 对象…...

家用洗地机应该怎么选?哪个牌子好?市场上主流洗地机品牌推荐
洗地机的出现,让越来越多的家庭享受清洁的过程,给人们腾出来更多的时间陪伴家人和休息。但是在选购一台洗地机前,大家多多少少肯定有些疑问,洗地机到底实不实用?好不好用?能扫干净吗?还有哪些好…...

python Django REST framework允许你根据API的版本提供不同的行为或数据
在Django REST framework中,版本控制是一个重要的功能,它允许你根据API的版本提供不同的行为或数据。以下是如何在Django REST framework中设置API版本控制的几种方法: 1. 使用URL路径参数 你可以通过URL路径中的参数来指定API的版本。例如: python复制 # urls.py from …...

unity给物体添加可以包裹所有子物体的BoxCollider
代码如下可直接调用 MeshTool.SpawnCollider(mode);using UnityEngine;public class MeshTool {public static Bounds SpawnCollider(Transform target){Vector3 pMax Vector3.zero;Vector3 pMin Vector3.zero;Vector3 center Vector3.zero;Vector3 oldPos target.transfor…...
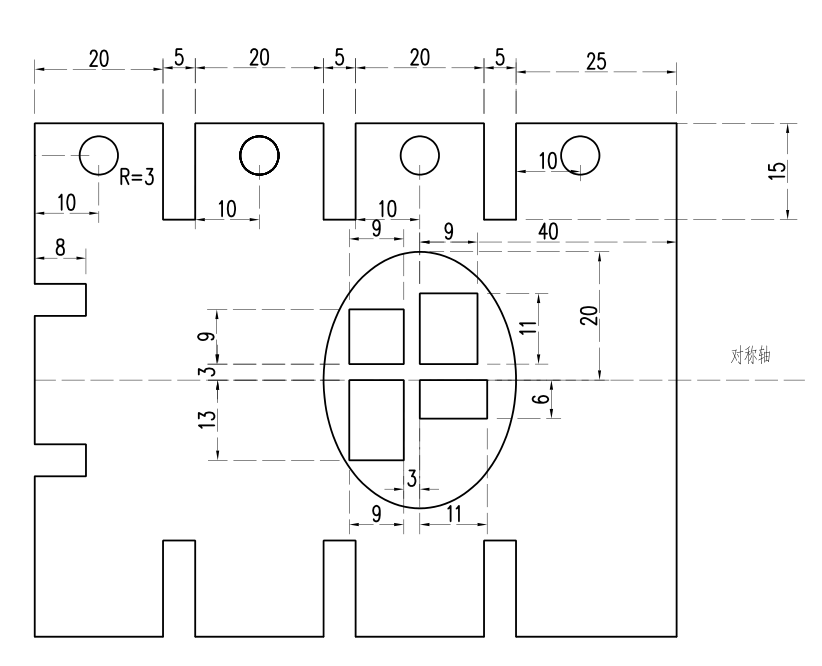
2024五一数学建模A题思路代码与论文分析
2024五一数学建模A题完整代码和成品论文获取↓↓↓↓↓ https://www.yuque.com/u42168770/qv6z0d/gyoz9ou5upvkv6nx?singleDoc# 2024五一数学建模A题钢板最优切割路径问题需要建立的模型和算法: 图论 最短路径算法(Dijkstra算法、Floyd算法等) 动态规划 网格化离散建模 …...
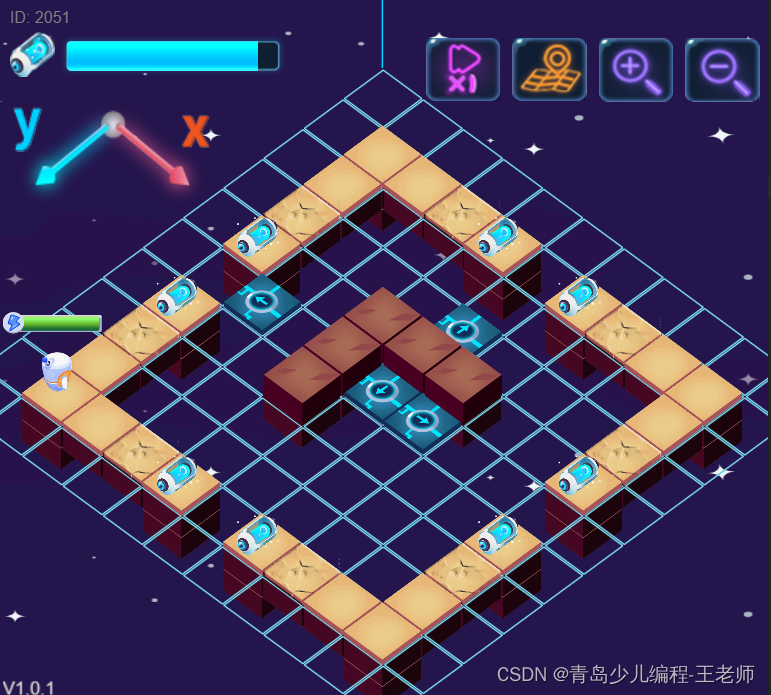
ICode国际青少年编程竞赛- Python-1级训练场-基础训练2
ICode国际青少年编程竞赛- Python-1级训练场-基础训练2 1、 a 4 # 变量a存储的数字是4 Dev.step(a) # 因为变量a的值是4,所以Dev.step(a)就相当于Dev.step(4)2、 a 1 # 变量a的值为1 for i in range(4):Dev.step(a)Dev.turnLeft()a a 1 # 变量a的值变为…...

科技控必看!让你轻松成为机器人领域达人
科技控们注意了!你是不是经常对机器人技术充满无限的好奇,却又因为缺乏合适的渠道而难以深入了解和亲身体验呢?别担心,BFT机器人,正是你探索机器人世界的绝佳之地! 在这里,你将发现一个充满惊喜…...

Linux进程——Linux下常见的进程状态
前言:在进程学习这一块,我们主要学习的就是PCB这个进程控制块,而PBC就是用来描述进程的结构体,而进程状态就是PCB结构体中的一个变量。 本篇主要内容: 操作系统中的进程状态Linux下的进程状态 在开始之前,我…...

TCP长连接短链接
1、短连接 短连接是指通讯双方有数据交互时,就建立一个连接,数据发送完成后,则断开此连接,即每次连接只完成一项业务的发送。 2、长连接 长连接是指在一个连接上可以连续发送多个数据包,在连接保持期间,…...

代码随想录35期Day33-Java
Day33题目 LeetCode1005:K 次取反后最大化的数组和 核心思想:每次取反都取反最小的。如果有负数,则一直取反最小的负数,如果没有就取反正数。取反次数只需要看是奇数还是偶数。偶数则正数序列不变,奇数则最小的变成负数 class …...
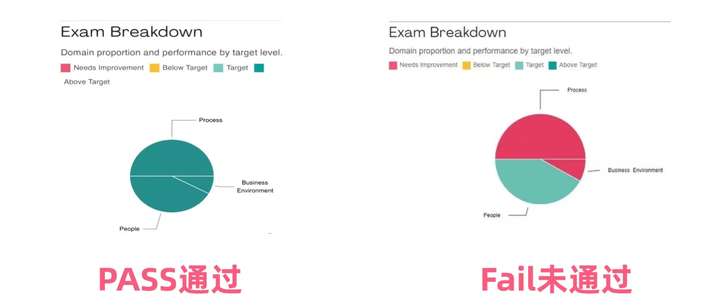
PMP考试没过怎么办?如何补考?(附复核流程)
最近刷小红书,看很多人都在晒PMP通过的成绩截图,一方面为大家开心,终于拿到了期盼已久的PMP,但同时也有宝子发挥失常没通过考试,所以这期针对没考过的宝子们,出一期复盘文章,无论结果如何&#…...
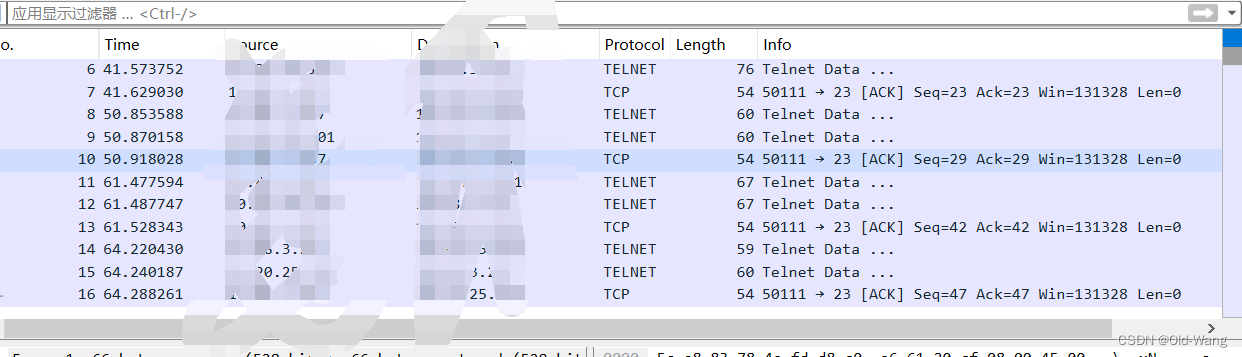
自主实现Telnet流量抓取
自主实现Telnet流量抓取 根据测试需求,需要抓取Telnet流量包,使用wireshark Python(socket、telnetlib库)实现 实现代码 主要此处有坑, 根据协议规则,wireshark 默认端口为23 的是Telnet协议࿰…...

以瓦片地图为底图添加图表,保留拖拽功能
1、问题1 在地图上覆盖一个容器层,容器层上的内容显示不出来如何解决? 原因:堆叠指数问题 解决方案:绝对定位后,提升其z-index值即可 2、问题2 在地图上覆盖一个容器层,影响了地图拖拽,如何…...

Windows cmd bat之特殊符号及变量
cmd 常用变量 bat批处理常用命令 %1~%9表示拖入文件(%0以外的输入文件),%0表示批处理文件本身 %0~%1字母意思基本相同,不区分大小写 ::打印当前窗口地址 echo “%cd%” %0 获取当前文件路径 %~d0 …...
用python写个控制MicroSIP自动拨号和定时呼叫功能(可用在小型酒店叫醒服务)
首先直接上结果吧,MicroSIP 助手,控制MicroSIP自动拨号,定时呼叫的非常实用小工具! 在使用MicroSIP 助手之前,我们需要了解MicroSIP是什么,MicroSIP是一个SIP拨号软件,支持注册任意SIP平台实现拨…...

axios 取消token 模糊搜索
import axios from ‘axios’; // 创建一个取消令牌源(cancel token source) const CancelToken axios.CancelToken; const source CancelToken.source(); // 下拉框搜索函数 function search() { // 获取输入值 const inputValue document.getElem…...

【OTS4WORD】“精简并行过程”——容易剪裁的“软件过程改进方法和规范”模板
附件资源是作者针对SPP采用模板重新格式化打包制作,原模板具有格式不受控的缺点,导致文档编制过程中引起不必要的排版麻烦。 附件资源适用于希望改进工作流程,适配CMMI质量管理体系的公司或个人使用,质量改进管理组织、项目管理组…...

22 | MySQL有哪些“饮鸩止渴”提高性能的方法?
短连接风暴 第一种方法:先处理掉那些占着连接但是不工作的线程。 kil id 第二种方法:减少连接过程的消耗。 让数据库跳过权限验证阶段,重启数据库,并使用–skip-grant-tables 参数启动。 慢查询性能问题 索引没有设计好 创建索引都支持 Online DDL 了,对于那种高峰期数…...

【AIGC调研系列】VILA-1.5版本的视频理解功能如何
VILA-1.5版本的视频理解功能表现出色,具有显著的突破。这一版本不仅增强了视频理解能力,还提供了四种不同规模的模型供用户选择,以适应不同的应用需求和计算资源限制[1][2][3]。此外,VILA-1.5支持在笔记本等边缘设备上部署&#x…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

C++:多态机制详解
目录 一. 多态的概念 1.静态多态(编译时多态) 二.动态多态的定义及实现 1.多态的构成条件 2.虚函数 3.虚函数的重写/覆盖 4.虚函数重写的一些其他问题 1).协变 2).析构函数的重写 5.override 和 final关键字 1&#…...

GO协程(Goroutine)问题总结
在使用Go语言来编写代码时,遇到的一些问题总结一下 [参考文档]:https://www.topgoer.com/%E5%B9%B6%E5%8F%91%E7%BC%96%E7%A8%8B/goroutine.html 1. main()函数默认的Goroutine 场景再现: 今天在看到这个教程的时候,在自己的电…...

(一)单例模式
一、前言 单例模式属于六大创建型模式,即在软件设计过程中,主要关注创建对象的结果,并不关心创建对象的过程及细节。创建型设计模式将类对象的实例化过程进行抽象化接口设计,从而隐藏了类对象的实例是如何被创建的,封装了软件系统使用的具体对象类型。 六大创建型模式包括…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

大数据治理的常见方式
大数据治理的常见方式 大数据治理是确保数据质量、安全性和可用性的系统性方法,以下是几种常见的治理方式: 1. 数据质量管理 核心方法: 数据校验:建立数据校验规则(格式、范围、一致性等)数据清洗&…...
