[C++][数据结构]AVL树插入的模拟实现
前言
紧接着上一篇文章,我们来模拟实现一下set的底层结构
引入
对于BSTree,虽然可以缩短查找的效率,但如果数据有序它将退化为单支树
我们可以用AVL树来解决这个问题。
概念
AVL树:
- 它的每个结点的左右子树高度之差的绝对值不超过1
- 它的左右子树都是AVL树
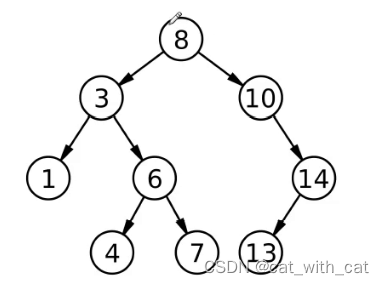 对于10来说,左右子树高度差为2,所以不满足
对于10来说,左右子树高度差为2,所以不满足
实现
基本结构
template<class K, class V>
struct AVLTreeNode
{using Node = AVLTreeNode<K, V>;Node* _left; //左节点Node* _right; //右节点Node* _parent //父节点int _bf; //平衡因子//计算方式:右树高度减去左树高度pair<K, V> _kv; //用pair封起来的键值对AVLTreeNode(const pair<K, V>& kv):_kv(kv),_bf(0),_left(nullptr),_right(nullptr),_parent(nullptr){}
};
插入
和搜索树的插入规则前半部分是相同的,具体细节可以看注释
bool Insert(const pair<K, V>& kv){//1.按照搜索树规则插入:先找到合适的位置,然后链接if (_root == nullptr){_root = new Node(kv);return true;}//如果树为空,特殊判断Node* parent = nullptr;//父节点//方便记录父节点原来的子树Node* cur = _root;while (cur != nullptr){if (cur->kv.first > kv.first){parent = cur;cur = cur->_left;}else if (cur->kv.first < kv.first){parent = cur;cur = cur->_right;}else{return false;}}//查找完再判断是父节点的左树还是右数//标记为Acur = new Node(kv);if (parent->kv.first > kv.first){parent->_right = cur;}else{parent->_right = cur;}cur->_parent = parent;//2.更新平衡因子,根据AVL的规则,进行旋转调整// - 插入因子会影响自己所有的祖先节点// - 更新原则:// 1.修改_bf// - cur是_parent左边,_parent->_bf--// - cur是_parent右边,_parent->_bf++// 2.根据_parent->_bf是否为0来判断是否修改祖先的_bf,// - _bf == 0 在更新前_bf是-1或1,更新后左右平衡了,所以不会影响祖先// - _bf == 1/-1 更新前平衡因子为0,更新后左右不平衡了,所以祖先也要更新// 3._bf == 2/-2 插入后出现问题,要进行旋转while(parent){if (parent->_right == cur){parent->_bf++;}else{parent->_bf--;}if (parent->_bf == 0){break;}else if (parent->_bf == 1 || parent->_bf == 1){cur = cur->_parent;parent = parent->_parent;}else if (parent->_bf == 2 || parent->_bf == -2){if (parent->_bf == 2 && cur->_bf == 1){RotateL(parent);}else if(parent->_bf == -2 && cur->_bf == -1){RotateR(parent);}else if (parent->_bf == -2 && cur->_bf == 1){RotateLR(parent);}else{RotateRL(parent);}break;//因为旋转完就是全都平衡了,所以直接结束循环}else{throw("false");}}return true;}
旋转
旋转也是插入的一部分,只是因为比较重要,所以单独拎出来写
变量说明:
- h表示树的高度
- a、b、c是树的名字
- 30,60是_value
左单旋
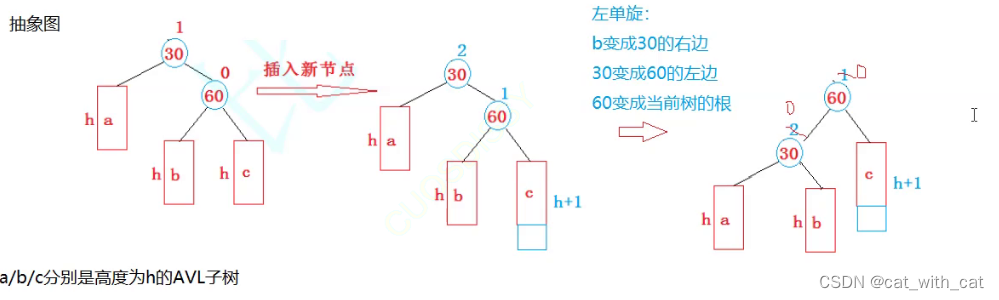
左单旋适合的情况:
右树插入新的节点,导致祖先节点不平衡
操作:
- 将右节点的左子树变为祖先节点的右子树
- 将祖先节点变为父节点的左子树
void RotateL(Node* parent) //右单旋
{Node* subR = parent->_right; //subR是parent的右节点Node* subRL = subR->_left; //subRL是subR的左节点parent->_right = subRL;if (subRL){subRL->_parent = parent;}subR->_left = parent;parent->_parent = subR;if (parent == _root){_root = subR;subR->_parent = nullptr;}else{if (parent->_parent->_left == parent){parent->_parent->_left = subR;}else{parent->_parent->_right = subR:}subR->_parent = parent->_parent;}parent->_bf = 0;subR->_bf = 0;
}
右单旋
和上面的逻辑相同,只是新增节点放在了左子树,要向右旋转
void RotateR(Node* parent) //右单旋{Node* subL = parent->_left; //subL是parent的左节点Node* subLR = subL->_right; //subLR是subL的右节点parent->_left = subLR;if (subLR){subLR->_parent = parent;}subL->_right = parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (parent->_parent->_left == parent){parent->_parent->_left = subL;}else{parent->_parent->_right = subL:}subL->_parent = parent->_parent;}parent->_bf = 0;subL->_bf = 0;}
左右双旋
旋转的代码相同,就是对于平衡因子的处理需要注意
分四种情况考虑
void RotateLR(Node* parent){Node* subL = parent->_left;Node* subLR = subL->_right;int bf = subLR->_bf;RotateL(parent->_left);RotateR(parent);if (bf == -1){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 1;}else if (bf == 1){subLR->_bf = 0;subL->_bf = -1;parent->_bf = 0;}else if (bf == 0){subLR->_bf = 0;subL->_bf = 0;parent->_bf = 0;}else{throw("false");}}右左双旋
void RotateRL(Node* parent){Node* subR = parent->_right;Node* subRL = subR->_left;int bf = subRL->_bf;RotateR(subR);RotateL(parent);subRL->_bf = 0;if (bf == 1){subR->_bf = 0;parent->_bf = -1;}else if (bf == -1){parent->_bf = 0;subR->_bf = 1;}else{parent->_bf = 0;subR->_bf = 0;}}
判断是否平衡
我们再写一个接口来判断给的树是否平衡
int _Height(Node* root){if (root == nullptr){return 0;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;}bool _IsBlance(Node* root){if (root == nullptr){return true;}int leftHeight = Height(root->_left);int rightHeight = Height(root->_right);if (abs(leftHeight - rightHeight) >= 2){throw("不平衡");}if (rightHeight - leftHeight != root->_bf){throw("平衡因子异常");}return _IsBlance(root->_left)&& _IsBlance(root->_right);}
优化:求高度
我们可以发现,这段代码还可以优化,因为每一次的高度都是要重新求的,有很多重复工作。
所以,我们可以增加一个参数,
bool _IsBlance(Node* root, int& height);
这样树的高度就会再函数调用结束后被传出来,并且不用修改返回值
bool _IsBalance(Node* root, int& height){if (root == nullptr){height = 0;return true;}int leftHeight = 0, rightHeight = 0;if (!_IsBalance(root->_left, leftHeight) || !_IsBalance(root->_right, rightHeight)){return false;}if (abs(rightHeight - leftHeight) >= 2){cout <<root->_kv.first<<"不平衡" << endl;return false;}if (rightHeight - leftHeight != root->_bf){cout << root->_kv.first <<"平衡因子异常" << endl;return false;}height = leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;return true;}bool IsBalance(){int height = 0;return _IsBalance(_root, height);}结语
AVL树比搜索树要更优秀,但具体逻辑(指旋转)要更复杂,希望对你有帮助!!
相关文章:

[C++][数据结构]AVL树插入的模拟实现
前言 紧接着上一篇文章,我们来模拟实现一下set的底层结构 引入 对于BSTree,虽然可以缩短查找的效率,但如果数据有序它将退化为单支树 我们可以用AVL树来解决这个问题。 概念 AVL树: 它的每个结点的左右子树高度之差的绝对值…...
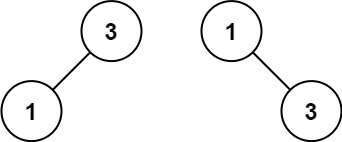
力扣每日一题108:将有序数组转换为二叉搜索树
题目 简单 给你一个整数数组 nums ,其中元素已经按 升序 排列,请你将其转换为一棵 平衡 二叉搜索树。 示例 1: 输入:nums [-10,-3,0,5,9] 输出:[0,-3,9,-10,null,5] 解释:[0,-10,5,null,-3,null,9] 也…...

保护公司机密:避免员工带着数据说拜拜
公司的核心资产之一就是数据。无论是客户信息、研发代码、内部决议、财务报告、商业合同、设计图纸等都是公司的重要资产。如果这些数据在员工离职时被带走,或在员工在职期间不当行为导致数据泄露,将给公司带来重大损失。 然而,保护这些数据…...
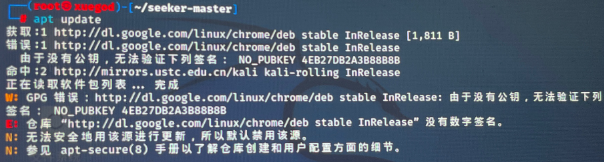
kali apt update报错
错误信息: 获取:http:/dl.google.com/几inux/chrome/.deb stable InRelease 错误:http:/dl.google.com/linux/chrome/deb stable InRelease 由于没有公钥,无法验证下列签名:NO_PUBKEY4EB27DB2A3B88B8B 命中:…...

7-1 图图图
某城市有n个景点,部分景点之间有巴士免费来回接送。(1) 给定某个景点x,如果从这个景点出发坐一次免费巴士,可以到达多少个不同的景点?(2) 判断景点a是否可以通过免费巴士(可换乘)到达景点b;(3) …...
)
Java(多线程)
取水: 主部分: package a0506.Test3;import java.util.Random;public class Test3 {public static void main(String[] args) {Well2 well2new Well2(10);WellThread Zsnew WellThread("------张三------",well2,new Random().nextInt(5));W…...

程序员必备的7大神器,效率飞起!
我们都知道程序员在工作时,会经常遇到任务繁重的情况,为了提高效率,程序员们也会借助一些软件,那么哪些软件可以帮助程序员们提高工作效率呢? 整理不易,关注一波!! 1. Xftp 7 Xft…...
揭秘文件加密利器:24年度最值得信赖的5大加密软件评测
数据安全与隐私保护已成为我们每个人都必须面对的重要问题。 文件加密软件作为保障数据安全的关键工具,其重要性不言而喻。 在众多的加密软件中,哪些软件能够在保障数据安全的同时,又具备良好的易用性和稳定性呢? 本文将为您揭秘…...
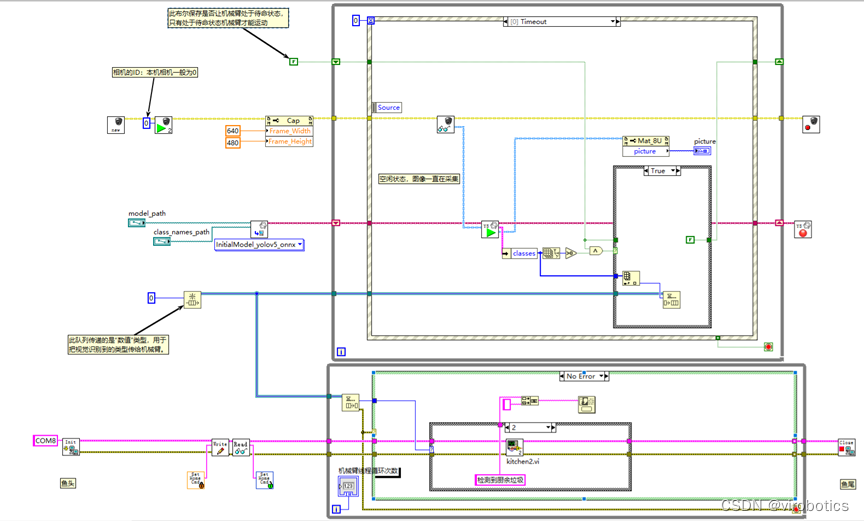
【仪酷LabVIEW AI工具包案例】使用LabVIEW AI工具包+YOLOv5结合Dobot机械臂实现智能垃圾分类
🏡博客主页: virobotics(仪酷智能):LabVIEW深度学习、人工智能博主 🎄所属专栏:『仪酷LabVIEW AI工具包案例』 📑上期文章:『【YOLOv9】实战二:手把手教你使用TensorRT实现YOLOv…...

鸿蒙应用开发系列 EX篇:HarmonyOS应用开发者基础认证
文章目录 系列文章背景认证考试题库参考注意:题库会不定时的进行具备调整甚至整体轮换,此为2024.5月版本注意:题库中题目的选项每次都会随机顺序,请参考内容判断题单选题多选题系列文章 鸿蒙应用开发系列 篇一:鸿蒙系统概述 鸿蒙应用开发系列 篇二:鸿蒙系统开发工具与环…...

基于Linux中的 进程相关知识 综合讲解
目录 一、进程的基本概念 二、pid,ppid,fork函数 三、进程的状态讲解 四、进程的优先级 五、完结撒❀ 一、进程的基本概念 概念: ● 课本概念:程序的一个执行实例,正在执行的程序等 ● 内核观点:担当…...
前端高频面试题 5.08
事件委托 事件委托是前端开发中常用的一种优化性能和代码可维护性的方法,它基于DOM的事件冒泡机制。当一个元素触发事件时,这个事件会按照从顶层到底层的顺序传播,直到最底层的元素(通常是文档的根节点)。事件委托利用…...

python 的继承、封装和多态
1. 继承(Inheritance) 继承是面向对象编程中的一个重要概念,它允许一个类(子类)继承另一个类(父类)的属性和方法。子类可以重用父类的代码,同时也可以扩展或修改父类的行为。 常用…...

数智结合,智慧合同让法务管理发挥内在价值
在当今这个信息化、数字化飞速发展的时代,数据已成为企业重要的战略资源。法务管理作为企业内部控制和风险防范的重要环节,其重要性不言而喻。然而,传统的法务管理模式往往存在效率低下、信息孤岛、反应迟缓等问题。在这样的背景下࿰…...

Ubuntu 安装docker
1: 卸载旧版本 如果你曾经安装过旧版本的 Docker,首先需要卸载它们: sudo apt-get remove docker docker-engine docker.io containerd runc2: 安装依赖工具 安装一些必要的工具,以便后续的安装过程能够顺利进行: sudo apt-ge…...

【北京迅为】《iTOP-3588开发板快速烧写手册》-第8章 TF启动
RK3588是一款低功耗、高性能的处理器,适用于基于arm的PC和Edge计算设备、个人移动互联网设备等数字多媒体应用,RK3588支持8K视频编解码,内置GPU可以完全兼容OpenGLES 1.1、2.0和3.2。RK3588引入了新一代完全基于硬件的最大4800万像素ISP&…...

Helm 模板流程控制
Helm 的模板语言提供了多种控制结构,以允许模板作者根据条件逻辑生成模板内容。以下是 Helm 模板控制结构的核心内容总结: 控制结构 Helm 模板支持以下控制结构: if/else:用于创建条件语句,根据给定的条件包含或排除…...

Kansformer?变形金刚来自过去的新敌人
1.前言 多层感知器(MLPs),也被称为全连接前馈神经网络,是当今深度学习模型的基础组成部分。 MLPs在机器学习中扮演着至关重要的角色,因为它们是用于近似非线性函数的默认模型,这得益于通用近似定理所保证的表达能力。然而,MLPs真的是我们能构建的最佳非线性回归器吗?尽管ML…...

今晚 19:00 | 从这两个问题入手,带你了解数据要素相关税务问题
五一假期已经结束,返工后当然是继续劳动啦~数据要素系列直播《星光对话》第三期也将在今晚19:00,继续跟大家见面。 本期直播,依然由 星光数智咨询总监 刘靖 主讲,带来:《数据要素相关税务问题解读》。 主要围绕两个问题…...

《QT实用小工具·五十一》带动画的 CheckBox
1、概述 源码放在文章末尾 该项目实现了带动画效果的多选框,鼠标放在上面或者选中都会呈现炫酷的动画效果,demo演示如下: 项目部分代码如下所示: #ifndef LINEARCHECKBOX_H #define LINEARCHECKBOX_H#include <QCheckBox> …...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...

React从基础入门到高级实战:React 实战项目 - 项目五:微前端与模块化架构
React 实战项目:微前端与模块化架构 欢迎来到 React 开发教程专栏 的第 30 篇!在前 29 篇文章中,我们从 React 的基础概念逐步深入到高级技巧,涵盖了组件设计、状态管理、路由配置、性能优化和企业级应用等核心内容。这一次&…...

Python常用模块:time、os、shutil与flask初探
一、Flask初探 & PyCharm终端配置 目的: 快速搭建小型Web服务器以提供数据。 工具: 第三方Web框架 Flask (需 pip install flask 安装)。 安装 Flask: 建议: 使用 PyCharm 内置的 Terminal (模拟命令行) 进行安装,避免频繁切换。 PyCharm Terminal 配置建议: 打开 Py…...

CppCon 2015 学习:REFLECTION TECHNIQUES IN C++
关于 Reflection(反射) 这个概念,总结一下: Reflection(反射)是什么? 反射是对类型的自我检查能力(Introspection) 可以查看类的成员变量、成员函数等信息。反射允许枚…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...

中科院1区顶刊|IF14+:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点
中科院1区顶刊|IF14:多组学MR联合单细胞时空分析,锁定心血管代谢疾病的免疫治疗新靶点 当下,免疫与代谢性疾病的关联研究已成为生命科学领域的前沿热点。随着研究的深入,我们愈发清晰地认识到免疫系统与代谢系统之间存在着极为复…...
