动态规划专训8——背包问题
动态规划题目中,常出现背包的相关问题,这里单独挑出来训练
A.01背包
1.01背包模板题
【模板】01背包_牛客题霸_牛客网 (nowcoder.com)
你有一个背包,最多能容纳的体积是V。
现在有n个物品,第i个物品的体积为𝑣𝑖vi ,价值为𝑤𝑖wi。
(1)求这个背包至多能装多大价值的物品?
(2)若背包恰好装满,求至多能装多大价值的物品?
第一问
1.状态表示:用dp[ i ][ j ]表示选到第 i 个物品, 体积不超过 j ,物品的最大价值
2.状态转移方程:dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i - 1 ][ j - v[ i ] ] + w[ i ] )
3.初始化:无需初始化
4.填表顺序:从上往下每一行
5.返回值:dp[ n ][ V ]
注意:由于 j - v[ i ] 可能小于0,所以需要提前特判
第二问
1.状态表示:用dp[ i ][ j ]表示选到第 i 个物品, 体积恰好 j ,物品的最大价值
2.状态转移方程:dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i - 1 ][ j - v[ i ] ] + w[ i ] )
3.初始化:根据题目初始化(见注意)
4.填表顺序:从上往下每一行
5.返回值:dp[ n ][ V ]
注意:由于dp状态表示地特殊性,可能存在无法使状态存在的情况,所以我们规定用 - 1 来表示状态不存在,于是在 j >= 1使,dp[ 0 ][ j ] = -1,在打印值时,也需要提前特判
#include<iostream>
#include<vector>
#include<string.h>using namespace std;const int N = 1010;
int n, V, v[N], w[N];int dp[N][N];int main()
{cin >> n >> V;for(int i = 1; i <= n; ++i)cin >> v[i] >> w[i];for(int i = 1; i <= n; ++i)for(int j = 1; j <= V; ++j){dp[i][j] = dp[i - 1][j];if(j >= v[i]) dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}cout << dp[n][V] << endl;memset(dp, 0, sizeof dp);for(int j = 1; j <= V; ++j) dp[0][j] = -1;for(int i = 1; i <= n; ++i)for(int j = 1; j <= V; ++j){dp[i][j] = dp[i - 1][j];if(j >= v[i] && dp[i - 1][j - v[i]] != -1) dp[i][j] = max(dp[i][j], dp[i - 1][j - v[i]] + w[i]);}cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;return 0;
}这是二维ac代码
#include<iostream>
#include<vector>
#include<string.h>using namespace std;const int N = 1010;
int n, V, v[N], w[N];int dp[N];int main()
{cin >> n >> V;for(int i = 1; i <= n; ++i)cin >> v[i] >> w[i];for(int i = 1; i <= n; ++i)for(int j = V; j >= v[i]; --j)dp[j] = max(dp[j], dp[j - v[i]] + w[i]);cout << dp[V] << endl;memset(dp, 0, sizeof dp);for(int j = 1; j <= V; ++j) dp[j] = -1;for(int i = 1; i <= n; ++i)for(int j = V; j >= v[i]; --j)if(dp[j - v[i]] != -1) dp[j] = max(dp[j], dp[j - v[i]] + w[i]);cout << (dp[V] == -1 ? 0 : dp[V]) << endl;return 0;
}这是一维ac代码
2.分割等和子集
416. 分割等和子集
给你一个 只包含正整数 的 非空 数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等
1.状态表示:用dp[ i ][ j ]表示选到第 i 个数, 和恰好 j 情况是否存在
2.状态转移方程:dp[ i ][ j ] = dp[ i - 1 ][ j ] || ( j >= nums[ i - 1 ] && dp[ i - 1 ][ j - nums[ i - 1 ] ] )
3.初始化:根据题目初始化(见注意)
4.填表顺序:从上往下每一行
5.返回值:dp[ n ][ k ]
注意:将题目转换为找出数组和一半的子序列,k = sum / 2,这样当 j = 0时dp[ i ][ 0 ] = true,且如果sum是奇数也可以直接返回false
class Solution {
public:bool canPartition(vector<int>& nums) {int n = nums.size();int sum = 0;for(int e : nums) sum += e;if(sum % 2) return false;int k = sum / 2;vector<vector<bool>> dp(n + 1, vector<bool>(k + 1));for(int i = 0; i <= n; ++i) dp[i][0] = true;for(int i = 1; i <= n; ++i)for(int j = 1; j <= k; ++j)dp[i][j] = dp[i - 1][j] || (j >= nums[i - 1] && dp[i - 1][j - nums[i - 1]]);return dp[n][k]; }
};这是二维ac代码
class Solution {
public:bool canPartition(vector<int>& nums) {int n = nums.size();int sum = 0;for(int e : nums) sum += e;if(sum % 2) return false;int k = sum / 2;vector<bool> dp(k + 1);dp[0] = true;for(int i = 1; i <= n; ++i)for(int j = k; j >= nums[i - 1]; --j)dp[j] = dp[j] || dp[j - nums[i - 1]];return dp[k]; }
};这是一维ac代码
3.目标和
494. 目标和
给你一个非负整数数组 nums 和一个整数 target 。
向数组中的每个整数前添加 '+' 或 '-' ,然后串联起所有整数,可以构造一个 表达式 :
- 例如,
nums = [2, 1],可以在2之前添加'+',在1之前添加'-',然后串联起来得到表达式"+2-1"。
返回可以通过上述方法构造的、运算结果等于 target 的不同 表达式 的数目
转换
设正数和为a,负数和绝对值为b,则 a + b = sum, a - b = target,于是有a = (sum + target) / 2,所以只要找出和为a的子序列即可,注意当(sum + target) 是奇数以及 a 小于0时直接返回0
1.状态表示:用dp[ i ][ j ]表示选到第 i 个数, 和恰好 j 情况数目
2.状态转移方程:dp[ i ][ j ] = dp[ i - 1 ][ j ] + dp[ i - 1 ][ j - nums[ i - 1 ] ]
3.初始化:dp[ 0 ][ 0 ] = 1;
4.填表顺序:从上往下每一行
5.返回值:dp[ n ][ k ]
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0, n = nums.size();for(int e : nums) sum += e;int k = (target + sum) / 2;if(k < 0 || (sum + target) % 2) return false;vector<vector<int>> dp(n + 1, vector<int>(k + 1));dp[0][0] = 1;for(int i = 1; i <= n; ++i)for(int j = 0; j <= k; ++j){dp[i][j] = dp[i - 1][j];if(j >= nums[i - 1]) dp[i][j] += dp[i - 1][j - nums[i - 1]];}return dp[n][k];}
};这是二维ac代码
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0, n = nums.size();for(int e : nums) sum += e;int k = (target + sum) / 2;if(k < 0 || (sum + target) % 2) return false;vector<int> dp(k + 1);dp[0] = 1;for(int i = 1; i <= n; ++i)for(int j = k; j >= nums[i - 1]; --j)dp[j] += dp[j - nums[i - 1]];return dp[k];}
};这是一维ac代码
4.最后一块石头的重量
1049. 最后一块石头的重量 II
有一堆石头,用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
- 如果
x == y,那么两块石头都会被完全粉碎; - 如果
x != y,那么重量为x的石头将会完全粉碎,而重量为y的石头新重量为y-x。
最后,最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下,就返回 0。
转换,从数组中挑选一堆石头使其接近 sum / 2,再使剩下的石头重量与其做差即可
于是我们要找到重量小于 sum / 2 的最大重量
1.状态表示:用dp[ i ][ j ]表示选到第 i 个数,重量不大于 j 的最大重量
2.状态转移方程:dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i - 1 ][ j - nums[ i - 1 ] ] + nums[ i - 1 ] )
3.初始化:无需初始化
4.填表顺序:从上往下每一行
5.返回值:dp[ n ][ k ]
class Solution {
public:int lastStoneWeightII(vector<int>& nums) {int sum = 0, n = nums.size();for(int e : nums) sum += e;int k = sum / 2;vector<vector<int>> dp(n + 1, vector<int>(k + 1));for(int i = 1; i <= n; ++i)for(int j = 1; j <= k; ++j){dp[i][j] = dp[i - 1][j];if(j >= nums[i - 1]) dp[i][j] = max(dp[i][j], dp[i - 1][j - nums[i - 1]] + nums[i - 1]);}return sum - dp[n][k] * 2;}
};这是二维ac代码
class Solution {
public:int lastStoneWeightII(vector<int>& nums) {int sum = 0, n = nums.size();for(int e : nums) sum += e;int k = sum / 2;vector<int> dp(k + 1);for(int i = 1; i <= n; ++i)for(int j = k; j >= nums[i - 1]; --j)dp[j] = max(dp[j], dp[j - nums[i - 1]] + nums[i - 1]);return sum - dp[k] * 2;}
};这是一维ac代码
B.完全背包
5.完全背包模板题
【模板】完全背包_牛客题霸_牛客网 (nowcoder.com)
你有一个背包,最多能容纳的体积是V。
现在有n种物品,每种物品有任意多个,第i种物品的体积为𝑣𝑖vi ,价值为𝑤𝑖wi。
(1)求这个背包至多能装多大价值的物品?
(2)若背包恰好装满,求至多能装多大价值的物品?
第一问
1.状态表示:用dp[ i ][ j ]表示选到第 i 个物品, 体积不超过 j ,物品的最大价值
2.状态转移方程:dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i ][ j - v[ i ] ] + w[ i ] )
3.初始化:无需初始化
4.填表顺序:从上往下每一行
5.返回值:dp[ n ][ V ]
第二问
1.状态表示:用dp[ i ][ j ]表示选到第 i 个物品, 体积恰好 j ,物品的最大价值
2.状态转移方程:dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i ][ j - v[ i ] ] + w[ i ] )
3.初始化:根据题目初始化(见注意)
4.填表顺序:从上往下每一行
5.返回值:dp[ n ][ V ]
注意:由于dp状态表示地特殊性,可能存在无法使状态存在的情况,所以我们规定用 - 1 来表示状态不存在,于是在 j >= 1使,dp[ 0 ][ j ] = -1,在打印值时,也需要提前特判
#include<iostream>
#include<vector>
#include<string.h>using namespace std;const int N = 1010;
int n, V, v[N], w[N];int dp[N][N];int main()
{cin >> n >> V;for(int i = 1; i <= n; ++i)cin >> v[i] >> w[i];for(int i = 1; i <= n; ++i)for(int j = 1; j <= V; ++j){dp[i][j] = dp[i - 1][j];if(j >= v[i]) dp[i][j] = max(dp[i][j], dp[i][j - v[i]] + w[i]);}cout << dp[n][V] << endl;memset(dp, 0, sizeof dp);for(int j = 1; j <= V; ++j) dp[0][j] = -1;for(int i = 1; i <= n; ++i)for(int j = 1; j <= V; ++j){dp[i][j] = dp[i - 1][j];if(j >= v[i] && dp[i][j - v[i]] != -1) dp[i][j] = max(dp[i][j], dp[i][j - v[i]] + w[i]);}cout << (dp[n][V] == -1 ? 0 : dp[n][V]) << endl;return 0;
}这是二维ac代码
#include<iostream>
#include<vector>
#include<string.h>using namespace std;const int N = 1010;
int n, V, v[N], w[N];int dp[N];int main()
{cin >> n >> V;for(int i = 1; i <= n; ++i)cin >> v[i] >> w[i];for(int i = 1; i <= n; ++i)for(int j = v[i]; j <= V; ++j)dp[j] = max(dp[j], dp[j - v[i]] + w[i]);cout << dp[V] << endl;memset(dp, 0, sizeof dp);for(int j = 1; j <= V; ++j) dp[j] = -1;for(int i = 1; i <= n; ++i)for(int j = v[i]; j <= V; ++j)if(dp[j - v[i]] != -1) dp[j] = max(dp[j], dp[j - v[i]] + w[i]);cout << (dp[V] == -1 ? 0 : dp[V]) << endl;return 0;
}这是一维ac代码
6.零钱兑换
322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。
计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。
你可以认为每种硬币的数量是无限的
1.状态表示:用dp[ i ][ j ]表示选到第 i 个硬币, 价值恰好等于 j ,最小的数目
2.状态转移方程:dp[ i ][ j ] = min(dp[ i - 1 ][ j ], dp[ i ][ j - coins[ i - 1 ] ] + 1)
3.初始化:dp[ 0 ][ j ] = 0x3f3f3f3f
4.填表顺序:从上往下每一行
5.返回值:dp[ n ][ am ]
注意:由于可能选择方案无法构成 j ,用0x3f3f3f3f来表示该状态不存在,同时在返回值时也需特判
class Solution {
public:int coinChange(vector<int>& coins, int amount) {const int INF = 0x3f3f3f3f;int n = coins.size();vector<vector<int>> dp(n + 1, vector<int>(amount + 1));for(int j = 1; j <= amount; ++j) dp[0][j] = INF;for(int i = 1; i <= n; ++i)for(int j = 1; j <= amount; ++j){dp[i][j] = dp[i - 1][j];if(j >= coins[i - 1]) dp[i][j] = min(dp[i][j], dp[i][j - coins[i - 1]] + 1);}return (dp[n][amount] == INF ? -1 : dp[n][amount]);}这是二维ac代码
class Solution {
public:int coinChange(vector<int>& coins, int amount) {const int INF = 0x3f3f3f3f;int n = coins.size();vector<int> dp(amount + 1);for(int j = 1; j <= amount; ++j) dp[j] = INF;for(int i = 1; i <= n; ++i)for(int j = coins[i - 1]; j <= amount; ++j)dp[j] = min(dp[j], dp[j - coins[i - 1]] + 1);return (dp[amount] == INF ? -1 : dp[amount]);}
};这是一维ac代码
7.零钱兑换II
给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。
请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。
假设每一种面额的硬币有无限个。
题目数据保证结果符合 32 位带符号整数。
1.状态表示:用dp[ i ][ j ]表示选到第 i 个硬币, 价值恰好等于 j ,组合的总数
2.状态转移方程:dp[ i ][ j ] = dp[ i - 1 ][ j ] + dp[ i ][ j - coins[ i - 1 ] ]
3.初始化:dp[ 0 ][ 0 ] = 1;
4.填表顺序:从上往下每一行
5.返回值:dp[ n ][ am ]
class Solution {
public:int change(int amount, vector<int>& coins) {int n = coins.size();vector<vector<int>> dp(n + 1, vector<int>(amount + 1));dp[0][0] = 1;for(int i = 1; i <= n; ++i)for(int j = 0; j <= amount; ++j){dp[i][j] = dp[i - 1][j];if(j >= coins[i - 1]) dp[i][j] += dp[i][j - coins[i - 1]];}return dp[n][amount];}
};这是二维ac代码
class Solution {
public:int change(int amount, vector<int>& coins) {int n = coins.size();vector<int> dp(amount + 1);dp[0] = 1;for(int i = 1; i <= n; ++i)for(int j = coins[i - 1]; j <= amount; ++j)dp[j] += dp[j - coins[i - 1]];return dp[amount];}
};这是一维ac代码
8.完全平方数
给你一个整数 n ,返回 和为 n 的完全平方数的最少数量 。
完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9 和 16 都是完全平方数,而 3 和 11 不是。
1.状态表示:用dp[ i ][ j ]表示选到第 i 个数, 价值恰好等于 j ,所需平方数的最小数目
2.状态转移方程:dp[ i ][ j ] = dp[ i - 1 ][ j ] + dp[ i ][ j - i * i ] + 1
3.初始化:dp[ 0 ][ 0 ] = 1;其他全部初始化为0x3f3f3f3f
4.填表顺序:从上往下每一行
5.返回值:dp[ n ][ k ]
注意:由于题目的特殊性,这里的“体积” k = sqrt( n ),而对于状态表示无意义的dp我们用0x3f3f3f3f标识,同时,返回数据时也要特判
class Solution {
public:int numSquares(int n) {const int INF = 0x3f3f3f3f;int k = sqrt(n);vector<vector<int>> dp(k + 1, vector<int>(n + 1, INF));dp[0][0] = 0;for(int i = 1; i <= k; ++i)for(int j = 0; j <= n; ++j){dp[i][j] = dp[i - 1][j];if(j >= i * i) dp[i][j] = min(dp[i][j], dp[i][j - i * i] + 1);}return dp[k][n] == INF ? 0 : dp[k][n];}
};这是二维ac代码
class Solution {
public:int numSquares(int n) {const int INF = 0x3f3f3f3f;int k = sqrt(n);vector<int> dp(n + 1, INF);dp[0] = 0;for(int i = 1; i <= k; ++i)for(int j = i * i; j <= n; ++j)dp[j] = min(dp[j], dp[j - i * i] + 1);return dp[n] == INF ? 0 : dp[n];}
};这是一维ac代码
C.二维费用的背包问题
9.一和零
474. 一和零
给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的长度,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集
1.状态表示:用dp[ i ][ j ][ k ]表示选到第 i 个数,0 数目小于 j ,1数目小于 k 的最大字符串数
2.状态转移方程:dp[ i ][ j ][ k ] = max(dp[ i - 1 ][ j ][ k ], dp[ i - 1 ][ j - a ][ k - b ] + 1)
3.初始化:无需初始化
4.填表顺序:从上往下每一行
5.返回值:dp[ len ][ m ][ n ]
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {int len = strs.size();vector<vector<vector<int>>> dp(len + 1, vector<vector<int>>(m + 1, vector<int>(n + 1)));for(int i = 1; i <= len; ++i){string s = strs[i - 1];int a = 0, b = 0;for(auto e : s)if(e == '0') ++a;else ++b;for(int j = 0; j <= m; ++j)for(int k = 0; k <= n; ++k){dp[i][j][k] = dp[i - 1][j][k];if(j >= a && k >= b)dp[i][j][k] = max(dp[i][j][k], dp[i - 1][j - a][k - b] + 1);}}return dp[len][m][n];}
};这是二维ac代码
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {int len = strs.size();vector<vector<int>> dp(m + 1, vector<int>(n + 1));for(int i = 1; i <= len; ++i){string s = strs[i - 1];int a = 0, b = 0;for(auto e : s)if(e == '0') ++a;else ++b;for(int j = m; j >= a; --j)for(int k = n; k >= b; --k)dp[j][k] = max(dp[j][k], dp[j - a][k - b] + 1);}return dp[m][n];}
};这是一维ac代码
10.盈利计划
集团里有 n 名员工,他们可以完成各种各样的工作创造利润。
第 i 种工作会产生 profit[i] 的利润,它要求 group[i] 名成员共同参与。如果成员参与了其中一项工作,就不能参与另一项工作。
工作的任何至少产生 minProfit 利润的子集称为 盈利计划 。并且工作的成员总数最多为 n 。
有多少种计划可以选择?因为答案很大,所以 返回结果模 10^9 + 7 的值
1.状态表示:用dp[ i ][ j ][ k ]表示选到第 i 个计划,员工数目不大于 j ,利润不小于 k
2.状态转移方程:dp[ i ][ j ][ k ] = (dp[ i - 1 ][ j ][ k ] + dp[ i - 1 ][ j - g[ i - 1 ] ] [max(0, k - p[ i - 1 ] ) ] ) % a;
3.初始化:dp[ 0 ][ j ][ 0 ] = 1
4.填表顺序:从上往下每一行
5.返回值:dp[ m ][ n ][ mP ]
class Solution {
public:int profitableSchemes(int n, int mP, vector<int>& g, vector<int>& p) {const int a = 1e9 + 7;int m = g.size();vector<vector<vector<int>>> dp(m + 1, vector<vector<int>>(n + 1, vector<int>(mP + 1)));for(int j = 0; j <= n; ++j)dp[0][j][0] =1;for(int i = 1; i <= m; ++i)for(int j = 0; j <= n; ++j)for(int k = 0; k <= mP; ++k){dp[i][j][k] = dp[i - 1][j][k];if(j >= g[i - 1])dp[i][j][k] = (dp[i][j][k] + dp[i - 1][j - g[i - 1]][max(0, k - p[i - 1])]) % a;}return dp[m][n][mP];}
};这是二维ac代码
class Solution {
public:int profitableSchemes(int n, int mP, vector<int>& g, vector<int>& p) {const int a = 1e9 + 7;int m = g.size();vector<vector<int>> dp(n + 1, vector<int>(mP + 1));for(int j = 0; j <= n; ++j)dp[j][0] =1;for(int i = 1; i <= m; ++i)for(int j = n; j >= g[i - 1]; --j)for(int k = 0; k <= mP; ++k)dp[j][k] = (dp[j][k] + dp[j - g[i - 1]][max(0, k - p[i - 1])]) % a;return dp[n][mP];}
};这是一维ac代码
D.似包非包
11.组合总数IV
给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。
题目数据保证答案符合 32 位整数范围
1.状态表示:用dp[ i ]表示数 i 被构造的排列次数
2.状态转移方程:dp[ i ] += dp[ i - x ];
3.初始化:dp[ 0 ] = 1
4.填表顺序:从左往右
5.返回值:dp[ target ]
class Solution {
public:int combinationSum4(vector<int>& nums, int target) {vector<double> dp(target + 1);dp[0] = 1;for(int i = 1; i <= target; ++i)for(auto x : nums)if(i >= x)dp[i] += dp[i - x];return dp[target];}
};这是ac代码
12.不同的二叉搜索树
96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
1.状态表示:用dp[ i ]表示 1 到 n 可以组成二叉搜索数的个数
2.状态转移方程:dp[ i ] += dp[ k - 1 ] * dp[ i - k ] ;
3.初始化:dp[ 0 ] = 1
4.填表顺序:从左往右
5.返回值:dp[ n ]
class Solution {
public:int numTrees(int n) {vector<int> dp(n + 1);dp[0] = 1;for(int i = 1; i <= n; ++i)for(int k = 1; k <= i; ++k)dp[i] += dp[k - 1] * dp[i - k];return dp[n];}
};这是ac代码
相关文章:

动态规划专训8——背包问题
动态规划题目中,常出现背包的相关问题,这里单独挑出来训练 A.01背包 1.01背包模板题 【模板】01背包_牛客题霸_牛客网 (nowcoder.com) 你有一个背包,最多能容纳的体积是V。 现在有n个物品,第i个物品的体积为𝑣&am…...
软件杯 深度学习花卉识别 - python 机器视觉 opencv
文章目录 0 前言1 项目背景2 花卉识别的基本原理3 算法实现3.1 预处理3.2 特征提取和选择3.3 分类器设计和决策3.4 卷积神经网络基本原理 4 算法实现4.1 花卉图像数据4.2 模块组成 5 项目执行结果6 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 &a…...
学习笔记:【QC】Android Q - IMS 模块
一、IMS init 流程图 高清的流程图参考:【高清图,保存后可以放大看】 二、IMS turnon 流程图 高清的流程图参考:【高清图,保存后可以放大看】 三、分析说明 1、nv702870 不创建ims apn pdp 2、nv702811 nv702811的时候才创建…...

NodeMCU ESP8266 操作 SSD1306 OLED显示屏详解(图文并茂)
文章目录 1 模块介绍2 接线介绍3 安装SSD1306驱动库4 源码分析4.1 硬件兼容性4.2 可能存在的问题总结1 模块介绍 我们将在本教程中使用的OLED显示屏是SSD1306型号:单色0.96英寸显示屏,像素为12864,如下图所示。 OLED显示屏不需要背光,这在黑暗环境中会产生非常好的对比度。…...

不抽象:Increase API 设计原则
原文:Increase - 2024.04.26 (注:Increase 是一家提供金融技术服务的公司。) API 资源是 API 的实体或对象。决定如何为这些实体命名和建模可以说是设计 API 最难也是最重要的部分。您所公开的资源组织了用户对您的产品如何工作…...

mybatis调用数据库存储过程
mybatis调用数据库存储过程及常见属性详解 调用mapper String visitCode mapper.getVisitCode(objectMap);Dao层,xml文件代码编写 <select id"getVisitCode" parameterType"map" resultType"string" statementType"CALLAB…...

【git】发生冲突后回滚提交
gerrit 冲突, 无法合并到主干 那么先回滚 参考这里的 reset 操作: 回滚 到上一个提交 $ git reset --soft HEAD~1 # 數字表示移動到 HEAD後面第幾個刚提交的会撤回, stash 刚刚提交的 然后去pull 最新的 修改冲突: 最后再…...

ISO14229 -1 UDS诊断服务记录-001:0x34\0x36\0x37\0x31\0x19\0x14服务报文格式介绍
目录 1、34服务-请求下载 1.1、诊断请求格式 1.2、正响应格式 1.3、负响应格式 1.4、工程应用分析 2、36服务-传输数据 2.1、请求报文格式 2.2、正响应格式 2.3、负响应NRC 3、37服务-退出传输 3.1、报文格式 3.2、正响应格式 3.3、负响应NRC 4、31服务-例程控制 …...
使用 MediaMTX 和 FFmpeg 推拉 RTSP 流媒体
实时流传输协议 RTSP(Real-Time Streaming Protocol)是 TCP/IP 协议体系中的一个应用层协议,由哥伦比亚大学、网景和 RealNetworks 公司提交的 IETF RFC 标准。该协议定义了一对多应用程序如何有效地通过 IP 网络传送多媒体数据。RTSP 在体系…...
Mac 电脑安装 Raptor 流程图软件的方法
0. 安装逻辑 (1)运行 raptor,本质上需要 mac 能够运行 windows 程序,因此需要安装 .NET Runtime 7.0,这是微软程序运行必须的文件。 (2)运行 raptor 还需要安装依赖文件 mono-libgdiplus。 &am…...

W801学习笔记二十:宋词学习应用
前三章完成了唐诗的应用,本章将实现宋词的学习应用。 宋词与唐诗的区别不大,马上开始。 1、我们需要参考前面唐诗的方式,把宋词文本下载下来,并进行格式整理。 W801学习笔记十七:古诗学习应用——上 2、在菜单中添加…...

EPAI手绘建模APP转换模型和坐标系
(11) 模型转换 图 273 转换工具栏 ① 实体转成曲面,先选择需要转成曲面的实体模型,再点击该按钮。将选择的实体模型转成多个曲面。 ② 曲线转成NURBS样条曲线,先选择需要转成NURBS样条曲线的边模型,修改转换参数,将选…...

STM32快速入门(串口传输之USART)
STM32快速入门(串口传输之USART) 前言 USART串口传输能实现信息在设备之间的点对点传输,支持单工、半双工、全全双工,一般是有三个引脚:TX、RX、SW_RX(共地)。不需要一根线来同步时钟。最大优…...

什么是网络安全和网络隐私?
什么是网络安全?这个是我最感兴趣的话题,网络安全说白了就是在网络上的安全,跟现实中一样,现实中为了家里的安全,我们会给家门上锁,会装监控,农村的话可能还会养一条狗,只有我们让别人进我们家,别人才能进来,对于计算机来说也是一样的,我们会设置账户的密码,会设置防火墙,会安…...

树莓派变小路由器放出热点wifi
环境 树莓派4Bubuntu20 作用 树莓派放出wifi后,笔记本电脑连接树莓派的wifi,并且ip配置在一个网段,就可以互相通信(笔记本放出wifi,树莓派连接效果一样),这样的好处是树莓派只要一上电就会自…...

数据猎手:使用Java和Apache HttpComponents库下载Facebook图像
引言 在信息驱动的时代,互联网上的数据成为了无可比拟的宝藏。本文旨在探讨如何通过利用Java和Apache HttpComponents库,从全球最大的社交网络平台Facebook上获取图像数据。 作为全球最大的社交网络平台,Facebook聚集了数以亿计的用户&#…...

uniapp——阻止冒泡
点击事件阻止冒泡 click.stop"onSubmit"其他类型,比如视频: 最后加了一个 click.stop <view class"videoBox" v-if"item.video_url"><video :src"i.image(item.video_url)" :controls"true&quo…...
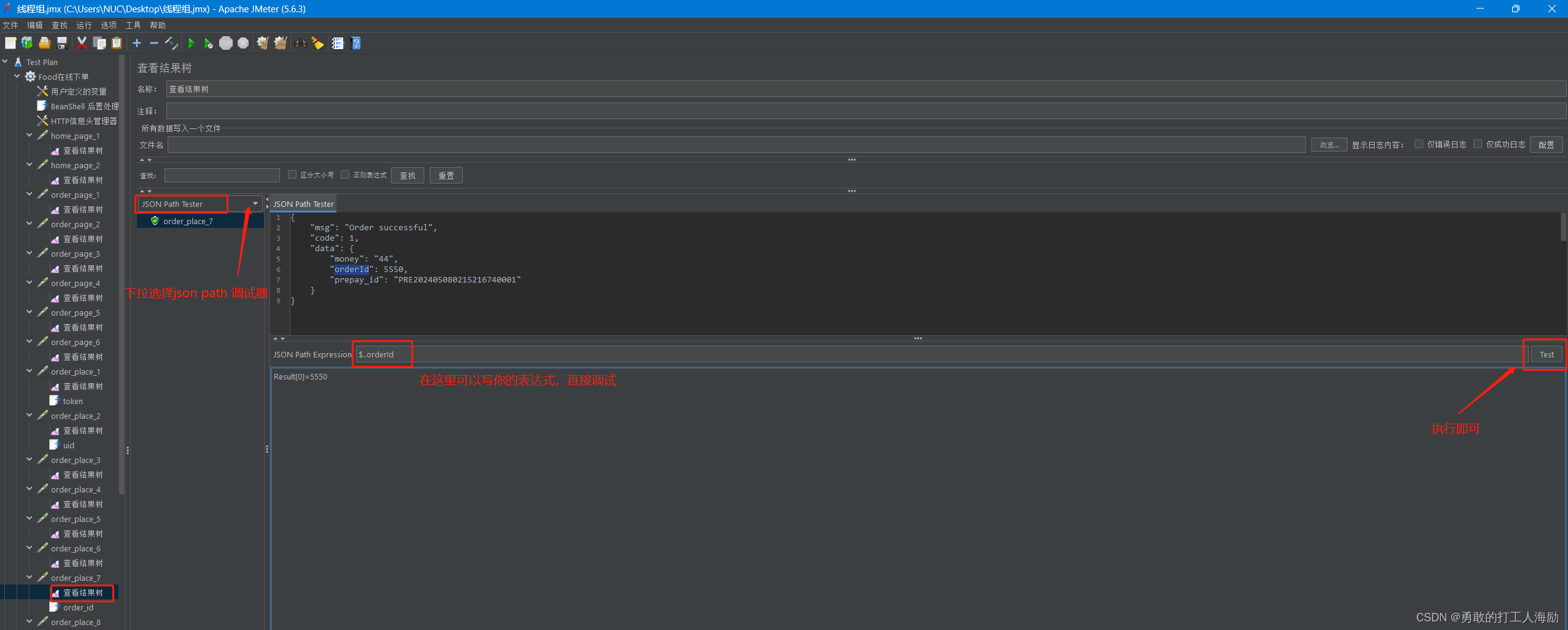
Jmeter性能测试(四)
一、遇到问题解决思路 1、检查请求头是否正确 2、检查请求参数是否正确 3、检查鉴权信息是否正确 4、检查变量作用域 5、检查数据提取是否正确(正则/json提取器) 二、请求头检查 1、在Http信息头管理器查看 2、注意这里的变量作用域是全局的 三、请求参数检查 1、在查看结…...

从零开始精通RTSP之传输ADPCM等音频流
概述 在上一篇文章中,我们详细介绍了使用RTP传输AAC音频流的打包方法。除了AAC编码算法外,常用的音频编码算法还有ADPCM、G711A、G711U、G726等。接下来,我们继续介绍RTP传输ADPCM等音频流的打包方法。 封装方法 RTP封装ADPCM等音频数据时&am…...
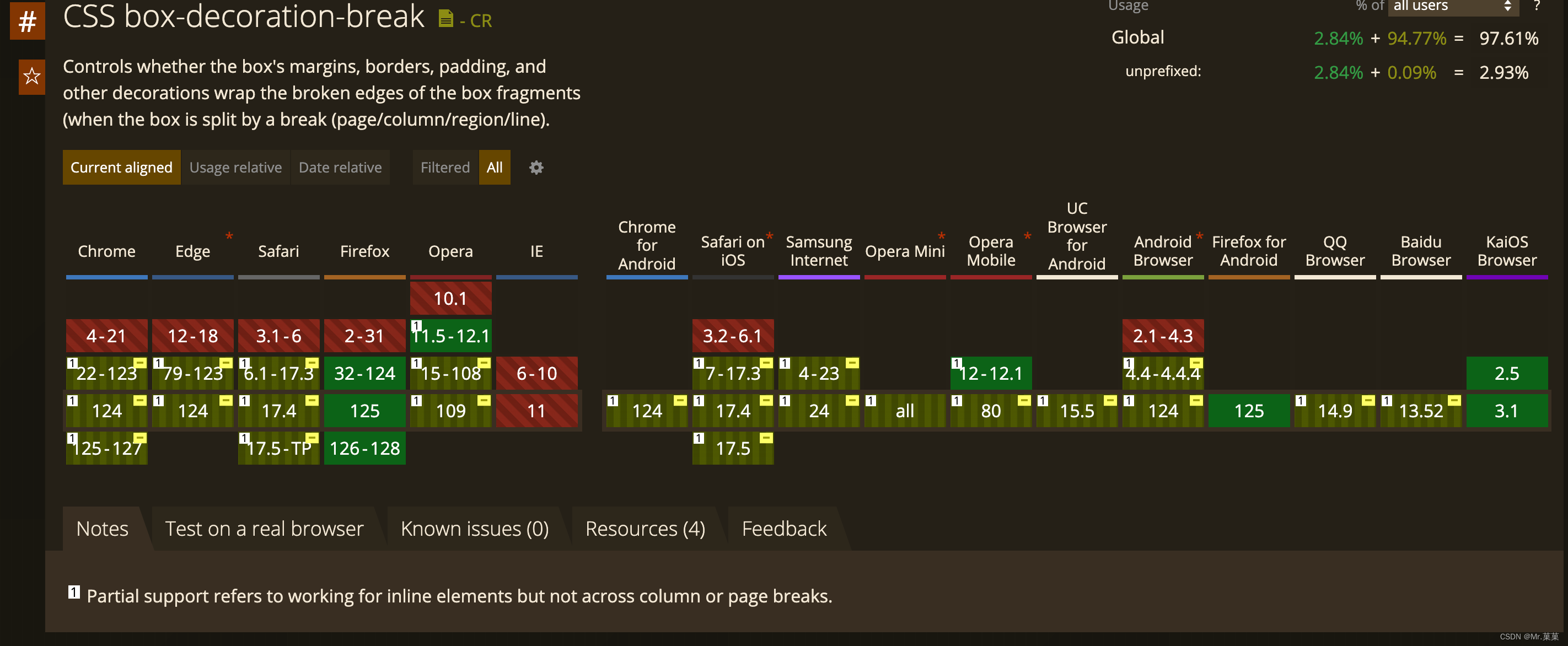
box-decoration-break 使用介绍
box-decoration-break属性的使用 一、定义 box-decoration-break是CSS片段模块(CSS Fragmentation Module Level 3)中的一个属性,主要用于指定背景(background)、内边距(padding)、边框&#…...

多云管理“拦路虎”:深入解析网络互联、身份同步与成本可视化的技术复杂度
一、引言:多云环境的技术复杂性本质 企业采用多云策略已从技术选型升维至生存刚需。当业务系统分散部署在多个云平台时,基础设施的技术债呈现指数级积累。网络连接、身份认证、成本管理这三大核心挑战相互嵌套:跨云网络构建数据…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

UR 协作机器人「三剑客」:精密轻量担当(UR7e)、全能协作主力(UR12e)、重型任务专家(UR15)
UR协作机器人正以其卓越性能在现代制造业自动化中扮演重要角色。UR7e、UR12e和UR15通过创新技术和精准设计满足了不同行业的多样化需求。其中,UR15以其速度、精度及人工智能准备能力成为自动化领域的重要突破。UR7e和UR12e则在负载规格和市场定位上不断优化…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

佰力博科技与您探讨热释电测量的几种方法
热释电的测量主要涉及热释电系数的测定,这是表征热释电材料性能的重要参数。热释电系数的测量方法主要包括静态法、动态法和积分电荷法。其中,积分电荷法最为常用,其原理是通过测量在电容器上积累的热释电电荷,从而确定热释电系数…...
