每日OJ题_记忆化搜索②_力扣62. 不同路径(三种解法)
目录
力扣62. 不同路径
解析代码1_暴搜递归(超时)
解析代码2_记忆化搜索
解析代码3_动态规划
力扣62. 不同路径
62. 不同路径
难度 中等
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
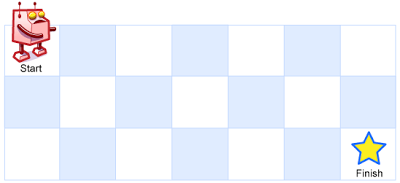
输入:m = 3, n = 7 输出:28
示例 2:
输入:m = 3, n = 2 输出:3 解释: 从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3 输出:28
示例 4:
输入:m = 3, n = 3 输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 10^9
class Solution {
public:int uniquePaths(int m, int n) {}
};解析代码1_暴搜递归(超时)
- 递归含义:给 dfs 一个下标,返回从 [0, 0] 位置走到 [i, j] 位置一共有多少种方法。
- 函数体:只要知道到达上面位置的方法数以及到达左边位置的方法数,然后累加起来即可。
- 递归出口:当下标越界的时候返回 0 ,当位于起点的时候,返回 1 。
class Solution {
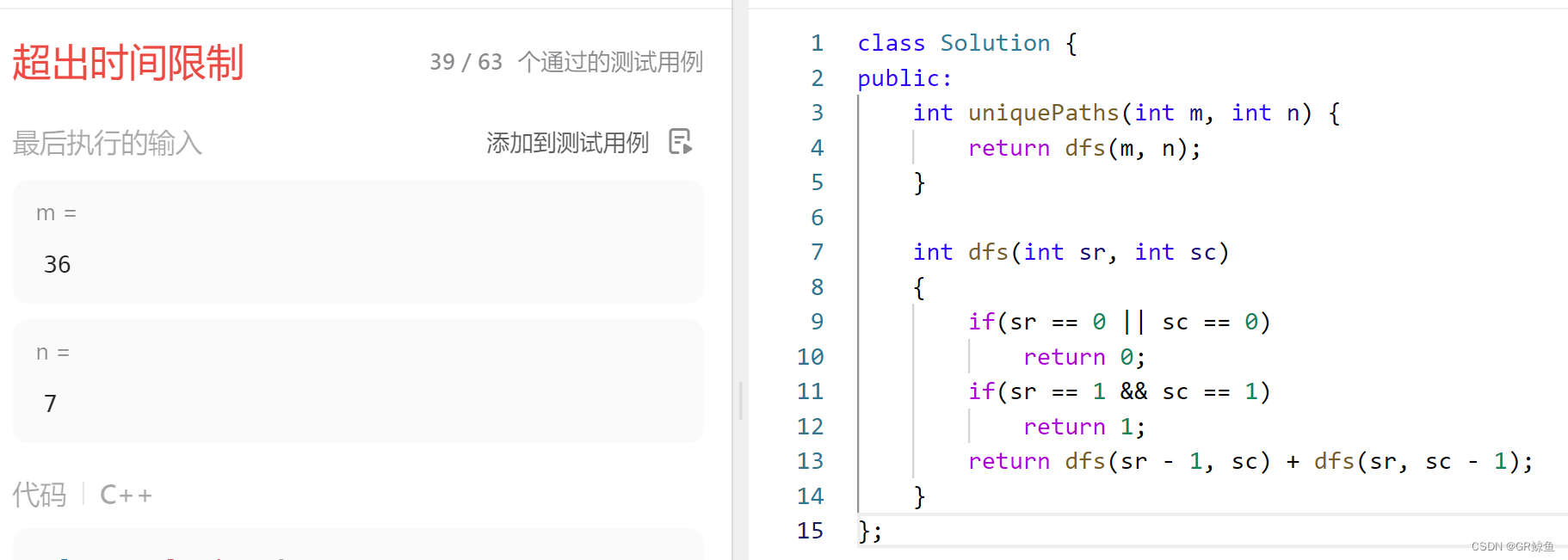
public:int uniquePaths(int m, int n) {return dfs(m, n);}int dfs(int sr, int sc){if(sr == 0 || sc == 0)return 0;if(sr == 1 && sc == 1)return 1;return dfs(sr - 1, sc) + dfs(sr, sc - 1);}
};
解析代码2_记忆化搜索
记忆化搜索解法:
- 加上一个备忘录。
- 每次进入递归的时候,去备忘录里面看看。
- 每次返回的时候,将结果加入到备忘录里面。
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> memo(m + 1, vector<int>(n + 1));return dfs(m, n, memo);}int dfs(int sr, int sc, vector<vector<int>>& memo){if(sr == 0 || sc == 0)return 0;if(sr == 1 && sc == 1)return 1;if(memo[sr][sc] != 0)return memo[sr][sc];memo[sr][sc] = dfs(sr - 1, sc, memo) + dfs(sr, sc - 1, memo);return memo[sr][sc];}
};
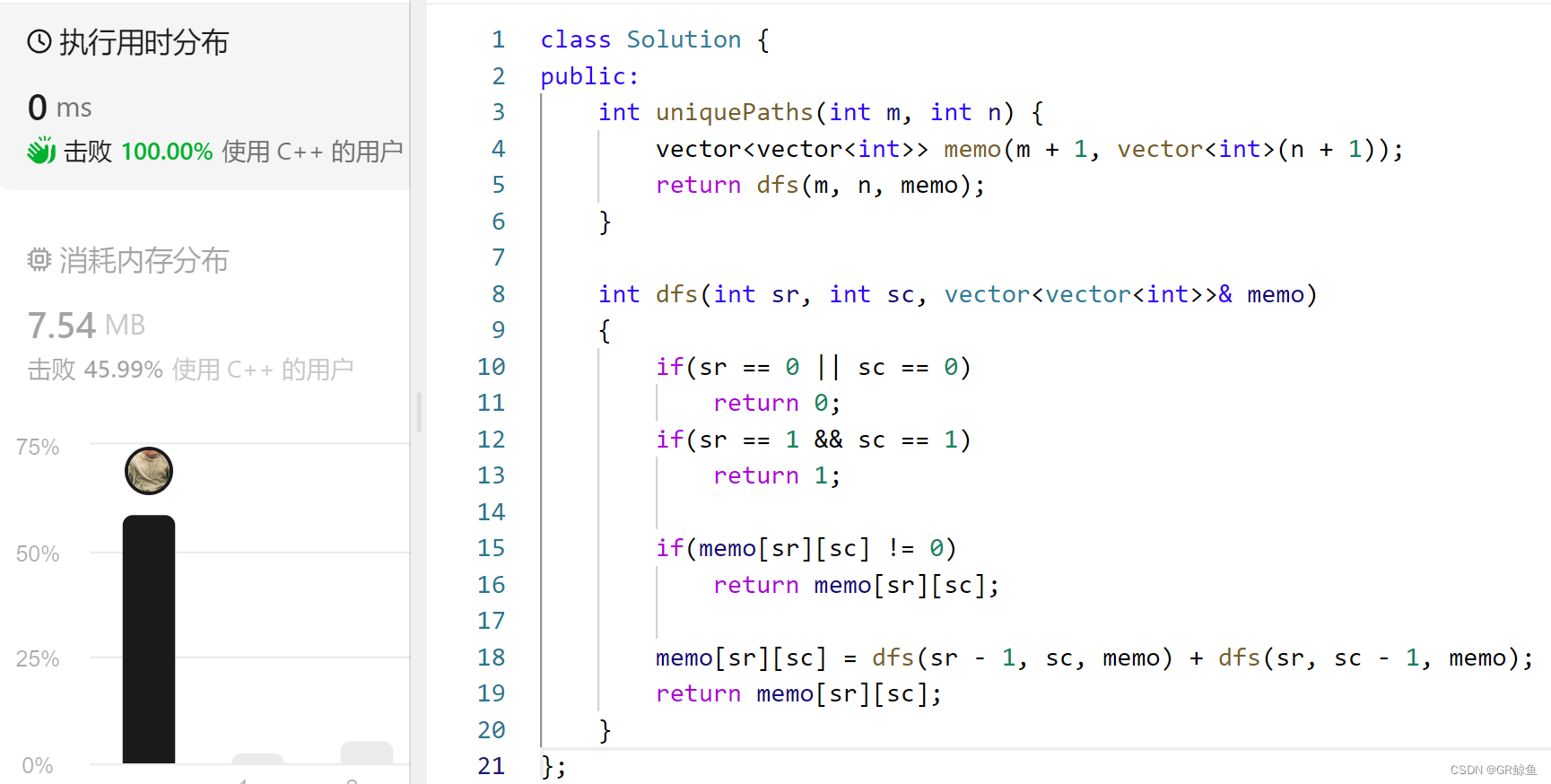
解析代码3_动态规划
根据记忆化搜索得出动态规划的解法:
- 递归含义:状态表示
- 函数体:状态转移方程
- 递归出口:初始化
- 填表顺序:填备忘录的顺序
- 返回值:备忘录的值
class Solution {
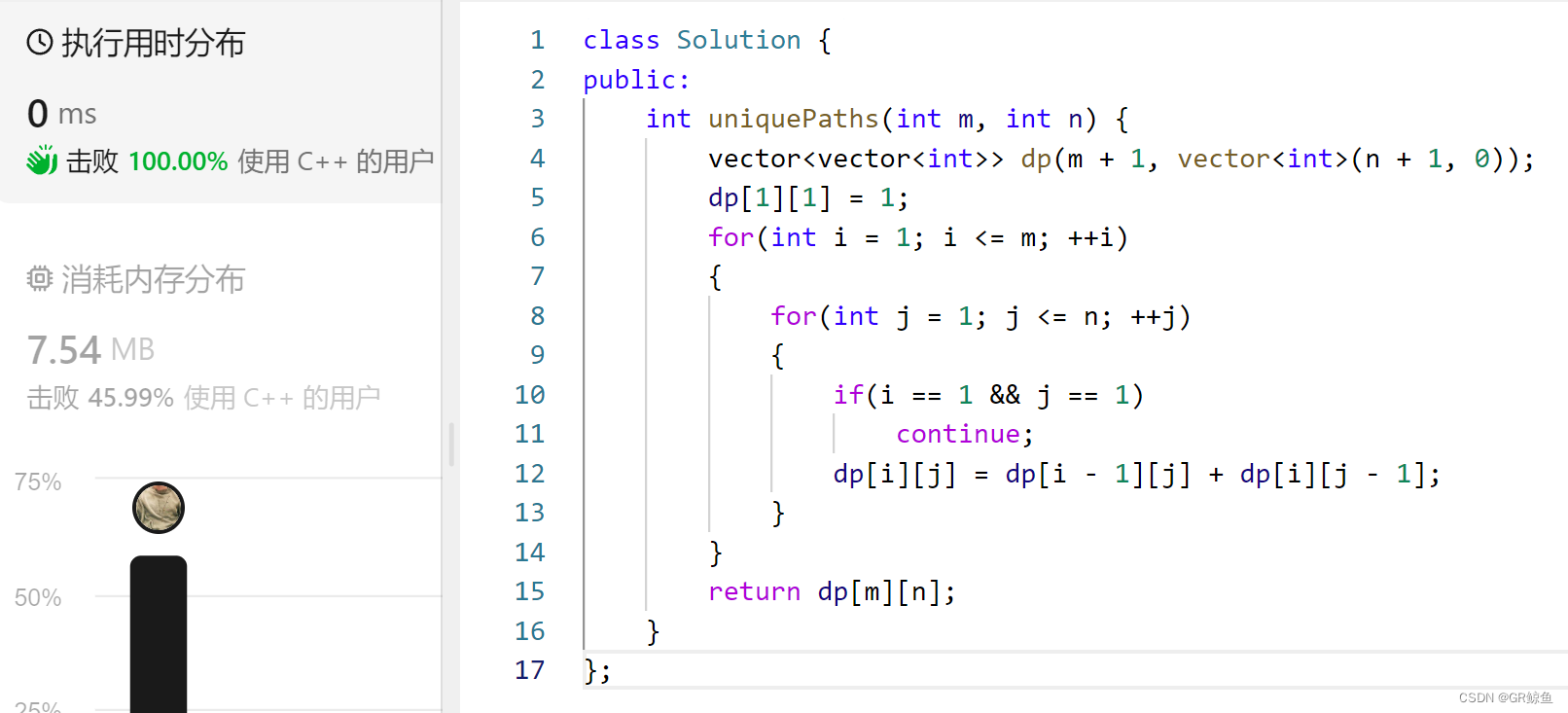
public:int uniquePaths(int m, int n) {vector<vector<int>> dp(m + 1, vector<int>(n + 1, 0));dp[1][1] = 1;for(int i = 1; i <= m; ++i){for(int j = 1; j <= n; ++j){if(i == 1 && j == 1)continue;dp[i][j] = dp[i - 1][j] + dp[i][j - 1];}}return dp[m][n];}
};
相关文章:

每日OJ题_记忆化搜索②_力扣62. 不同路径(三种解法)
目录 力扣62. 不同路径 解析代码1_暴搜递归(超时) 解析代码2_记忆化搜索 解析代码3_动态规划 力扣62. 不同路径 62. 不同路径 难度 中等 一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。 机器…...
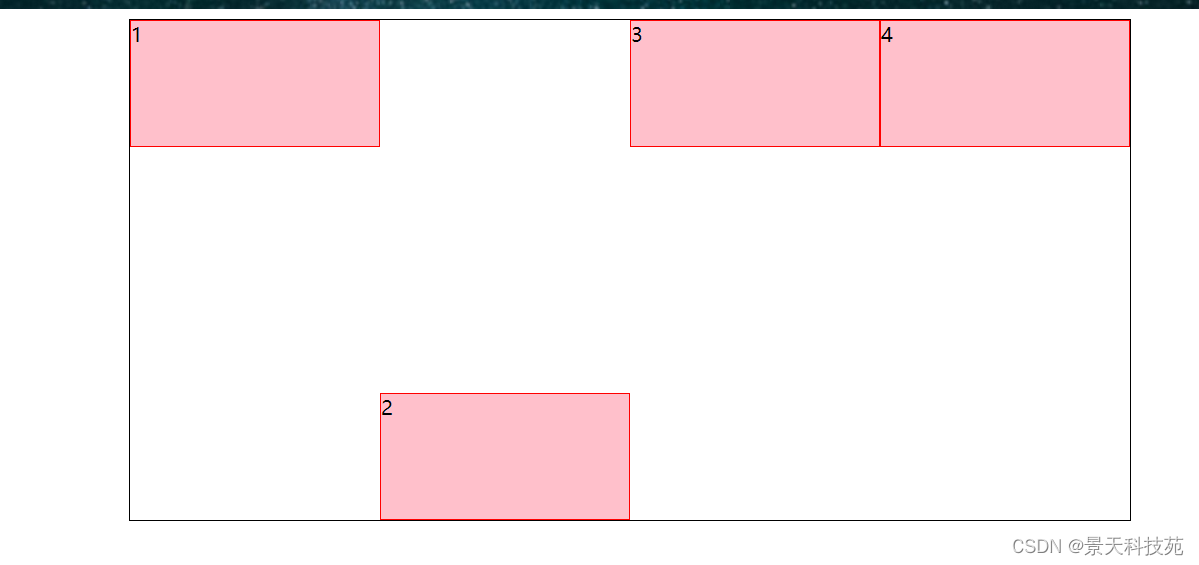
【微信小程序开发】微信小程序、大前端之flex布局方式详细解析
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...
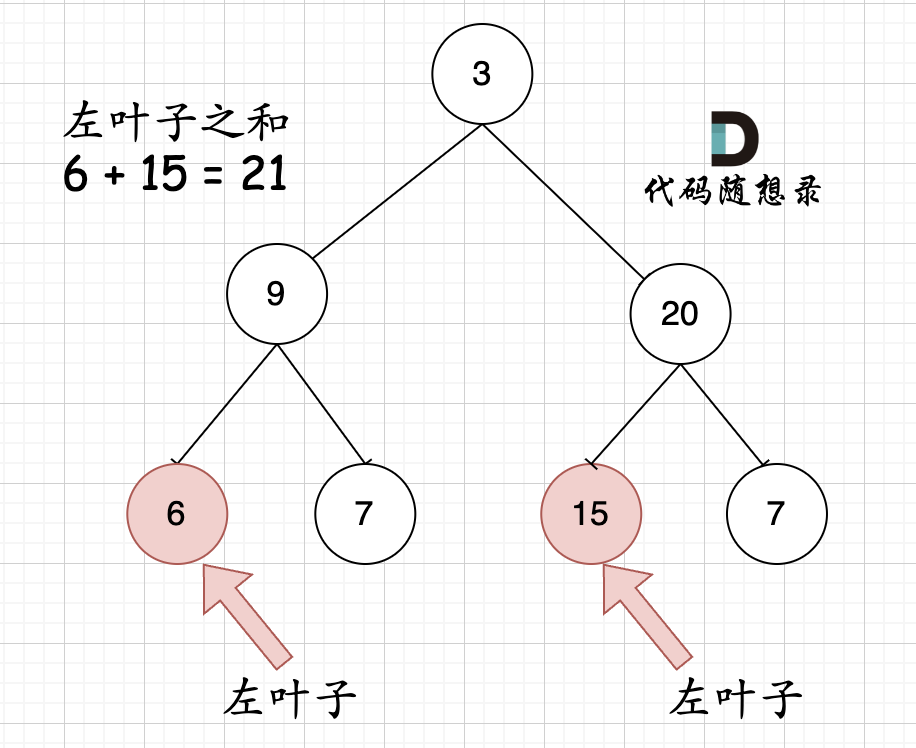
代码随想录算法训练营第二十天:二叉树成长
代码随想录算法训练营第二十天:二叉树成长 110.平衡二叉树 力扣题目链接(opens new window) 给定一个二叉树,判断它是否是高度平衡的二叉树。 本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝…...

Opensbi初始化分析:设备初始化-warmboot
Opensbi初始化分析:设备初始化-warmboot 设备初始化sbi_init函数init_warmboot函数coolboot & warmbootwait_for_coldboot函数domain && scratch(coldboot所特有)console初始化及print相关工作(coldboot所特有)系统调用的相关初始化(coldboot所特有)综上设备…...
)
软考 系统架构设计师系列知识点之软件可靠性基础知识(13)
接前一篇文章:软考 系统架构设计师系列知识点之软件可靠性基础知识(12) 所属章节: 第9章. 软件可靠性基础知识 第3节 软件可靠性管理 为了进一步提高软件可靠性,人们又提出了软件可靠性管理的概念,把软件可…...
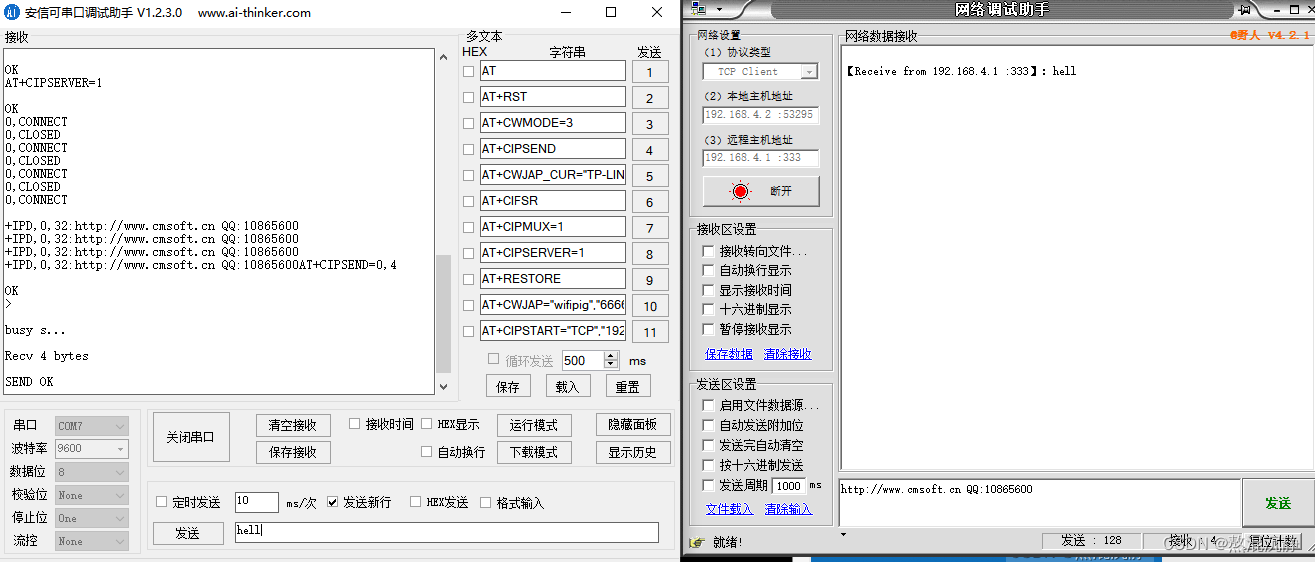
将ESP工作为AP路由模式并当成服务器
将ESP8266模块通过usb转串口接入电脑 ATCWMODE3 //1.配置成双模ATCIPMUX1 //2.使能多链接ATCIPSERVER1 //3.建立TCPServerATCIPSEND0,4 //4.发送4个字节在链接0通道上 >ATCIPCLOSE0 //5.断开连接通过wifi找到安信可的wifi信号并连接 连接后查看自己的ip地址变为192.168.4.…...
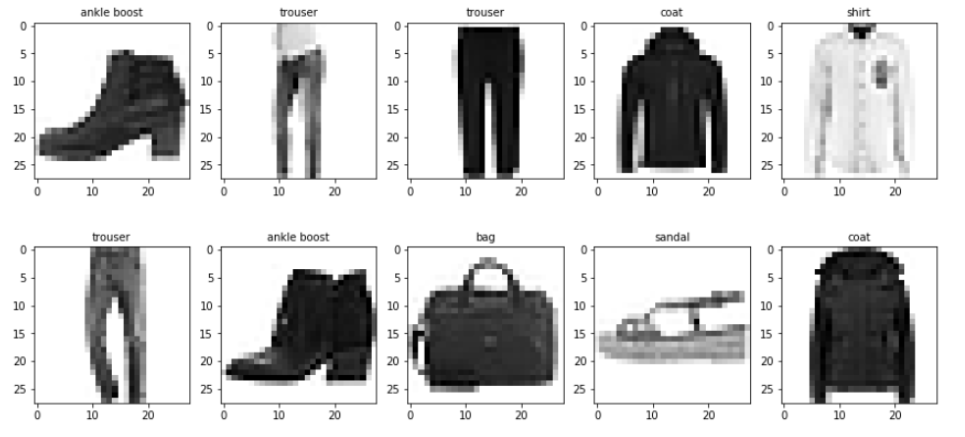
Python深度学习基于Tensorflow(6)神经网络基础
文章目录 使用Tensorflow解决XOR问题激活函数正向传播和反向传播解决过拟合权重正则化Dropout正则化批量正则化 BatchNormal权重初始化残差连接 选择优化算法传统梯度更新算法动量算法NAG算法AdaGrad算法RMSProp算法Adam算法如何选择优化算法 使用tf.keras构建神经网络使用Sequ…...

力扣HOT100 - 35. 搜索插入位置
解题思路: 二分法模板 class Solution {public int searchInsert(int[] nums, int target) {int left 0;int right nums.length - 1;while (left < right) {int mid left ((right - left) >> 1);if (nums[mid] target)return mid;else if (nums[mid…...
MinimogWP WordPress 主题下载——优雅至上,功能无限
无论你是个人博客写手、创意工作者还是企业站点的管理员,MinimogWP 都将成为你在 WordPress 平台上的理想之选。以其优雅、灵活和功能丰富而闻名,MinimogWP 不仅提供了令人惊叹的外观,还为你的网站带来了无限的创作和定制可能性。 无与伦比的…...
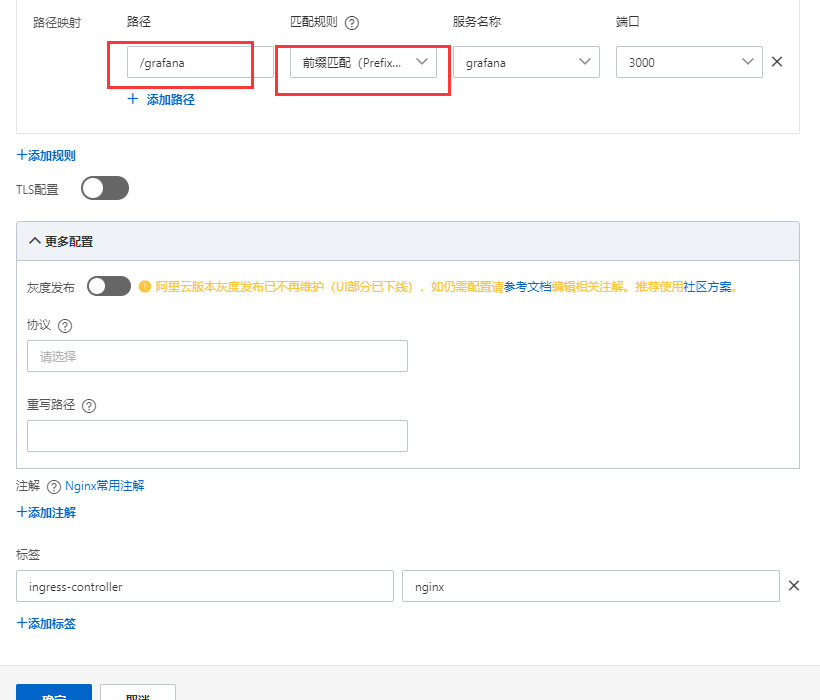
kube-prometheus部署到 k8s 集群
文章目录 **修改镜像地址****访问配置****修改 Prometheus 的 service****修改 Grafana 的 service****修改 Alertmanager 的 service****安装****Prometheus验证****Alertmanager验证****Grafana验证****卸载****Grafana显示时间问题** 或者配置ingress添加ingress访问grafana…...

从0开始学习python(六)
目录 前言 1、循环结构 1.1 遍历循环结构for 1.2 无限循环结构while 总结 前言 上一篇文章我们讲到了python的顺序结构和分支结构。这一章继续往下讲。 1、循环结构 在python中,循环结构分为两类,一类是遍历循环结构for,一类是无限循环结…...
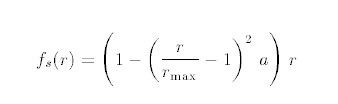
OpenGL 入门(三)—— OpenGL 与 OpenCV 共同打造大眼滤镜
从本篇开始,会在上一篇搭建的滤镜框架的基础上,介绍具体的滤镜效果该如何制作。本篇会先介绍大眼滤镜,先来看一下效果,原图如下: 使用手机后置摄像头对眼部放大后的效果: 制作大眼滤镜所需的主要知识点&…...
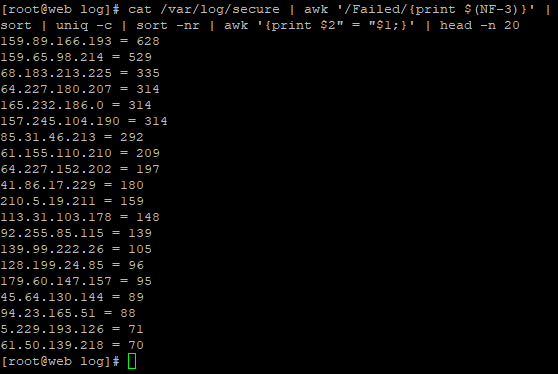
Linux服务器安全基础 - 查看入侵痕迹
1. 常见系统日志 /var/log/cron 记录了系统定时任务相关的日志 /var/log/dmesg 记录了系统在开机时内核自检的信息,也可以使用dmesg命令直接查看内核自检信息 /var/log/secure:记录登录系统存取数据的文件;例如:pop3,ssh,telnet,ftp等都会记录在此. /var/log/btmp:记…...

Java反射机制的实战应用:探索其魅力与局限
引言 Java作为一种面向对象的编程语言,其灵活性和强大的功能使其成为众多开发者的首选。而Java反射机制作为Java语言中的一项重要特性,为程序员提供了一种在运行时检查和操作类、方法、属性等信息的能力。本文旨在深入探讨Java反射机制的实战应用&#…...

vue3项目 文件组成
从头捋顺一遍vue3项目文件目录 前置知识JS模块化什么是依赖?安装依赖webpack能做什么?vue基本使用 不借助vue-cli,从0开始搭建vue项目。index.html、main.js、App.vue引入npm引入webpack引入babel引入vue-loaderwebpack配置webpack配置 前置知…...

C语言关键字 typedef 的功能是什么?
一、问题 语⾔有 32 个关键字,其中 int 的功能是声明整型变量,struct 的功能是声明结构体变量,那么 typedef 的功能是什么呢? 二、解答 1. typedef 的功能 在 C 语⾔中除了可以使⽤标准类型名(如 int、 char、float …...

【YoloDeployCsharp】基于.NET Framework的YOLO深度学习模型部署测试平台-源码下载与项目配置
基于.NET Framework 4.8 开发的深度学习模型部署测试平台,提供了YOLO框架的主流系列模型,包括YOLOv8~v9,以及其系列下的Det、Seg、Pose、Obb、Cls等应用场景,同时支持图像与视频检测。模型部署引擎使用的是OpenVINO™、TensorRT、ONNX runtime以及OpenCV DNN,支持CPU、IGP…...

如何在 Ubuntu 12.04 VPS 上使用 MongoDB 创建分片集群
简介 MongoDB 是一个 NoSQL 文档数据库系统,可以在水平方向上很好地扩展,并通过键值系统实现数据存储。作为 Web 应用程序和网站的热门选择,MongoDB 易于实现并可以通过编程方式访问。 MongoDB 通过一种称为“分片”的技术实现扩展。分片是将…...
阿里云VOD视频点播流程(1)
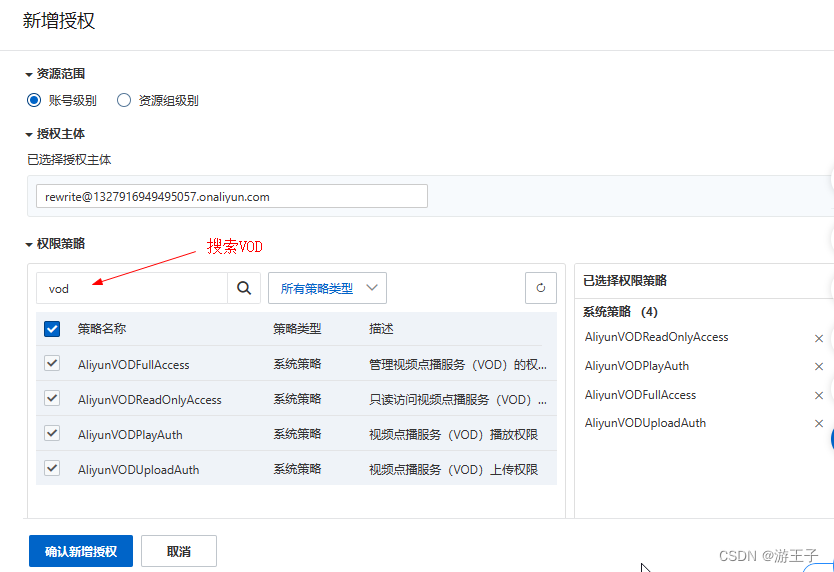
一、开通阿里云VOD 视频点播(ApsaraVideo VoD,简称VOD)是集视频采集、编辑、上传、媒体资源管理、自动化转码处理、视频审核分析、分发加速于一体的一站式音视频点播解决方案。登录阿里云,在产品找到视频点播VOD ,点击…...
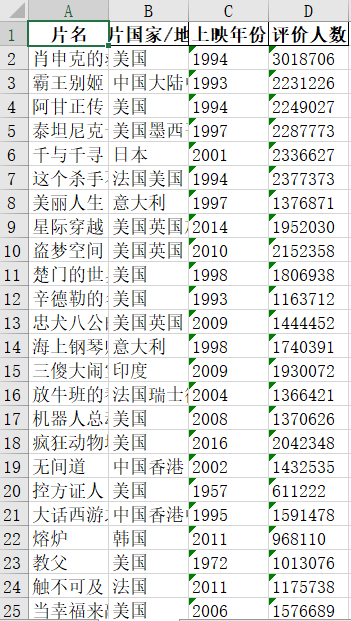
Python爬虫获取豆瓣电影Top100
大家好,我是秋意零。 今天分析一篇,Python爬虫获取豆瓣电影Top100。 在此之前,我没有学习过爬虫,只有一丢丢的Python基础。下面效果的实现源码几乎没经过我,而是AI百老师。我主要负责了对应的调试以及根据我想要的功…...

Docker 离线安装指南
参考文章 1、确认操作系统类型及内核版本 Docker依赖于Linux内核的一些特性,不同版本的Docker对内核版本有不同要求。例如,Docker 17.06及之后的版本通常需要Linux内核3.10及以上版本,Docker17.09及更高版本对应Linux内核4.9.x及更高版本。…...

k8s从入门到放弃之Ingress七层负载
k8s从入门到放弃之Ingress七层负载 在Kubernetes(简称K8s)中,Ingress是一个API对象,它允许你定义如何从集群外部访问集群内部的服务。Ingress可以提供负载均衡、SSL终结和基于名称的虚拟主机等功能。通过Ingress,你可…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Mac软件卸载指南,简单易懂!
刚和Adobe分手,它却总在Library里给你写"回忆录"?卸载的Final Cut Pro像电子幽灵般阴魂不散?总是会有残留文件,别慌!这份Mac软件卸载指南,将用最硬核的方式教你"数字分手术"࿰…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...
