搜索算法系列之三(插值查找)
前言
插值查找仅适用于有序数据、有序数组,和二分查找类似,更讲究数据有序均匀分布。
算法原理
插值查找(interpolation search)是一种查找算法,它与二分查找类似,但在寻找元素时更加智能化。这种算法假设数据集是等距的或者有序的,然后根据要查找的值在数据集中的位置进行估计,而不是简单地将查找范围划分为两半。
插值查找的步骤如下:
-
确定查找范围:首先确定要查找的元素在哪个范围内。通常情况下,这是通过比较要查找的值和数据集的第一个和最后一个元素来确定的。
-
计算估计位置:通过插值公式计算要查找的值在当前查找范围内的估计位置。插值公式通常是
(value - array[low]) / (array[high] - array[low]) * (high - low) + low,其中low和high分别是当前查找范围的起始和结束位置。 -
检查估计位置:将估计位置与要查找的值进行比较。
- 如果估计位置上的值等于要查找的值,则找到了目标元素。
- 如果估计位置上的值大于要查找的值,则在估计位置的左侧继续进行插值查找。
- 如果估计位置上的值小于要查找的值,则在估计位置的右侧继续进行插值查找。
-
重复直到找到目标元素或者确定元素不存在。
插值查找适用于数据集分布比较均匀的情况下,因为它是根据数据集的分布情况进行估计的。在数据集分布不均匀的情况下,插值查找可能会失效,效率不如二分查找。
上述公式说明:
value为查找的值。low、high为数据集首尾下标。array[low]、array[high]为数据集首尾值。
(value-array[low])/(array[high]-array[low])计算查找值在有序队列所处位置的比值。
代码实现(c)
#include <stdio.h>// 插值查找函数
int interpolationSearch(int arr[], int low, int high, int key) {if (low <= high) {// 计算插值的索引int mid = low + (high - low) * (double)((key - arr[low]) / (arr[high] - arr[low]));// 如果元素等于key,返回midif (arr[mid] == key)return mid;// 如果元素小于key,在右侧递归查找if (arr[mid] > key)return interpolationSearch(arr, low, mid - 1, key);// 如果元素大于key,在左侧递归查找return interpolationSearch(arr, mid + 1, high, key);}// 如果数组不存在key,返回-1return -1;
}int main() {int arr[] = {1, 2, 3, 4, 5, 6, 7, 8, 9};int n = sizeof(arr) / sizeof(arr[0]);int key = 7;// 查找元素int index = interpolationSearch(arr, 0, n - 1, key);// 输出结果if (index != -1)printf("元素在数组中的索引为: %d\n", index);elseprintf("元素不在数组中。\n");return 0;
}注意计算比例时转double类型,否则会失效。
优点与局限性
优点:
- 适用于均匀分布的数据集: 插值查找在数据集均匀分布时效果更为显著,能够更准确地估计目标值的位置。
- 相对于二分查找的改进: 在某些情况下,插值查找的效率较二分查找更高,尤其是对于近似均匀分布的数据。
局限:
- 对于不均匀分布的数据效果不佳: 当数据分布不均匀时,插值查找的性能可能较差,甚至不如二分查找。
- 可能导致溢出: 在计算插值位置时,由于分母可能为零,导致除法溢出的风险。
复杂度
插值查找的时间复杂度取决于数据集的分布情况。在理想情况下(即数据集均匀分布),插值查找的时间复杂度可以达到 O(log log n)。这是因为它根据数据集的分布情况进行估计,可以更快地缩小查找范围。
然而,在最坏情况下,插值查找的时间复杂度可以达到 O(n),这通常发生在数据集中存在大量重复元素或者数据集分布不均匀的情况下。在这种情况下,插值查找可能会退化为线性搜索,效率明显下降。
总体来说,插值查找在数据集分布均匀的情况下具有更好的性能,但在数据集分布不均匀或存在大量重复元素时,效率可能不如二分查找等其他查找算法。因此,在实际应用中,需要根据具体情况选择合适的查找算法。
相关文章:
)
搜索算法系列之三(插值查找)
前言 插值查找仅适用于有序数据、有序数组,和二分查找类似,更讲究数据有序均匀分布。 算法原理 插值查找(interpolation search)是一种查找算法,它与二分查找类似,但在寻找元素时更加智能化。这种算法假设数据集是等距的或者有…...
前端奇怪面试题总结
面试题总结 不修改下面的代码进行正常解构 这道题考的是迭代器和生成器的概念 let [a,b] {a:1,b:2}答案 对象缺少迭代器,需要手动加上 Object.prototype[Symbol.iterator] function* (){// return Object.values(this)[Symbol.iterator]()return yeild* Object.v…...

NPM--最新淘宝镜像源地址
最新淘宝镜像源地址: 原来的 https://registry.npm.taobao.org 已替换为 https://registry.npmmirror.com 查看镜像源 npm config get registry 更换为淘宝最新镜像源 npm config set registry https://registry.npmmirror.com...

vue3中实现地区下拉选择组件封装
1组件文件 新建一个文件夹内,包含inde.vue,index.ts,pac.json这三个文件 index.vue文件 <template><el-cascaderv-model"data":options"pcaData":style"{ width: props.width }":placeholder"props.placeholder&quo…...

责任链模式案例
需求背景: 请你设计一个员工休假审批流程,当员工的休假天数<1时,由直接领导审批,休假天数<2时,分别由直接领导、一级部门领导审批,休假天数>3时,分别由直接领导、一级部门领导、分管领…...
Android NDK开发(二)——JNIEnv、jobject与jclass关系
本文主要讲解Android NDK开发中JNIEnv、jobject与jclass的相关知识,并用c和c两种语言实现了jobject和jclass。 本专栏知识点是通过<零声教育>的音视频流媒体高级开发课程进行系统学习,梳理总结后写下文章,对音视频相关内容感兴趣的读者…...

机器学习入门:sklearn基础教程
Scikit-learn(简称sklearn)是Python中最受欢迎的机器学习库之一,它提供了丰富的机器学习算法和工具,适用于各种任务和场景。本文将为您介绍sklearn的基础知识和常用功能,带您踏入机器学习的世界。 1. 安装与导入 首先…...
26 | 备库为什么会延迟好几个小时?
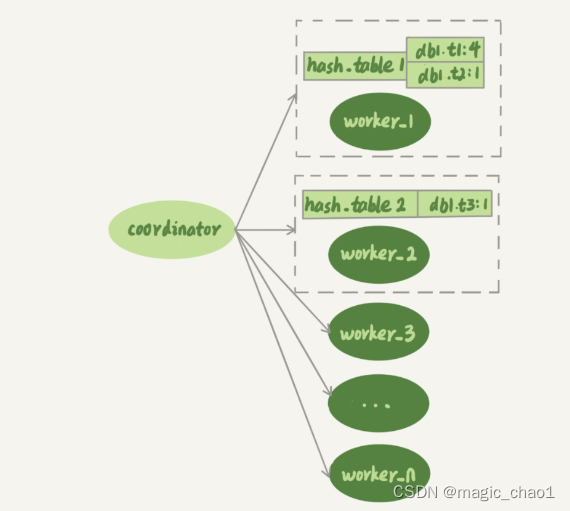
在官方的 5.6 版本之前,MySQL 只支持单线程复制,由此在主库并发高、TPS 高时就会出现严重的主备延迟问题。 coordinator 就是原来的 sql_thread, 不过现在它不再直接更新数据了,只负责读取中转日志和分发事务。真正更新日志的,变成了 worker 线程。而 work 线程的个数,就是…...

linux 如何解压.tar 文件
要在 Linux 中解压 tar 文件,请使用以下命令: tar -xvf yourfile.tar 1 其中,“yourfile.tar”是您要解压的文件名。 这个命令会将文件解压到当前目录中。如果想要将文件解压到不同的目录中,可以使用 -C 选项指定路径。例如&…...
盘点企业信息防泄密软件对比|揭秘企业信息防泄密软件好用榜
在当今信息化社会,企业信息防泄密软件的需求日益凸显。这些软件不仅关乎企业的核心竞争力,更直接关系到企业的生死存亡。本文将对市面上几款主流的企业信息防泄密软件进行深入对比分析,以期为企业提供有益的参考。 一、企业信息防泄密软件好…...

html--瀑布效果
<!doctype html> <html> <head> <meta charset"utf-8"> <title>瀑布效果</title><style> body {background: #222;color: white;overflow:hidden; }#container {box-shadow: inset 0 1px 0 #444, 0 -1px 0 #000;height: 1…...
vue视图不刷新强制更新数据this.$forceUpdate()
在vue中,更新视图数据,不刷新页面,需要强制更新数据才可以 前言 在对数据就行添加和删除时,发现页面视图不更新,排除发现需要强制更新才可以 点击添加或删除,新增数据和删除就行,但在不使用fo…...
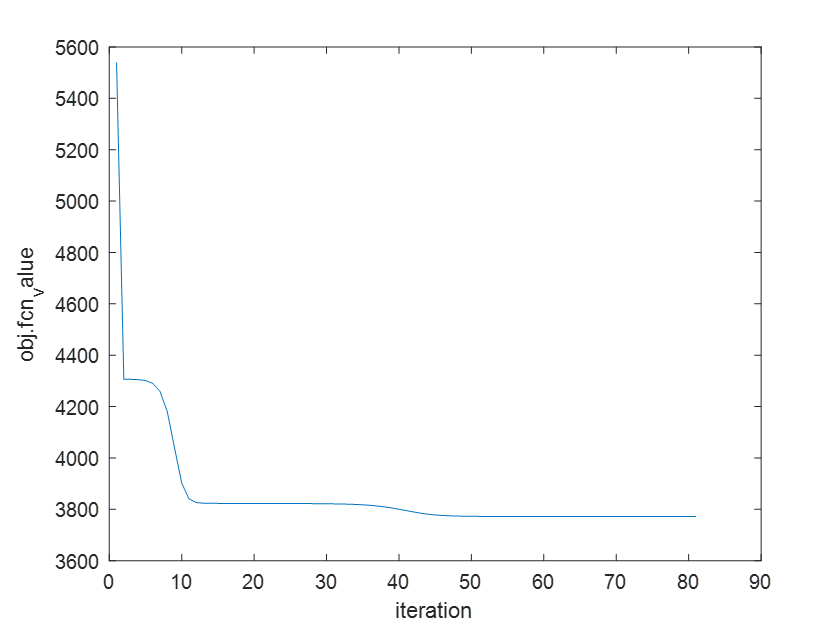
2024年电工杯数学建模竞赛A题B题思路代码分享
您的点赞收藏是我继续更新的最大动力! 一定要点击如下的卡片链接,那是获取资料的入口! 点击链接加入群聊【2024电工杯】:http://qm.qq.com/cgi-bin/qm/qr?_wv1027&kUMFX8lu4qAm0XkZQ6JkW5m5O9F_mxf-L&authKey0hWdf7%2F…...

leetcode 797.所有可能的路径
思路:dfs。 其实很简单,我们只需要和昨天做的题一样,直接遍历所给数组中的元素,因为这里的数组意义已经很清楚了,就是当前位置的结点和哪一个顶点有联系。 注意:在存储路径的时候,我们需要按顺…...

NPM 基础
介绍 npm 是 JavaScript 编程语言的一个包管理器,它允许开发者安装、共享和管理依赖项。npm 与 Node.js 紧密集成,是 Node.js 生态系统中不可或缺的一部分。它提供了一个命令行工具,使得开发者能够轻松地安装、配置和管理项目所需的各种包。…...
WPF之创建无外观控件
1,定义无外观控件。 定义默认样式,在其静态构造函数中调用DefaultStyleKeyProperty.OverrideMetadata()。 //设置默认样式DefaultStyleKeyProperty.OverrideMetadata(typeof(ColorPicker), new FrameworkPropertyMetadata(typeof(ColorPicker))); 在项目…...
MySQL利用变量进行查询操作
新建连接,自带world数据库,里面自带city表格。 # MySQL利用变量进行查询操作 set cityNameHaarlemmermeer; select * from city where NamecityName;# 多个结果查询 set cityName1Haarlemmermeer; set cityName2Breda; set cityName3Willemstad; selec…...

算法--动态规划
动态规划(Dynamic Programming, DP)是一种算法设计技巧,用于解决具有重叠子问题和最优子结构性质的问题。通过将原问题分解为相对简单的子问题的方式来求解复杂问题,动态规划避免了计算重复子问题,从而提高了算法的效率…...
Python基础详解一
一,print打印 print("hello word") print(hello word) 双引号和单引号都可以 二,数据类型 Python中常用的有6种值的类型 输出类型信息 print(type(11)) print(type("22")) print(type(22.2)) <class int> <class str&…...
3.SpringSecurity基本原理
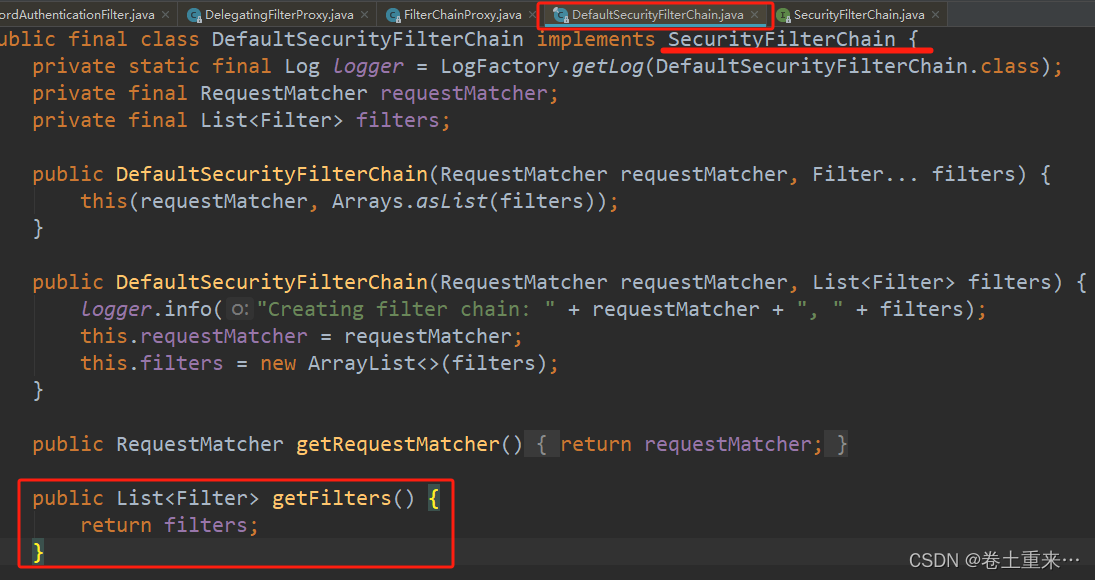
SpringSecurity本质是一个过滤器链。十多个过滤器构成一个过滤器链。 这些过滤器在项目启动就会进行加载。每个过滤器执行放行操作才会执行下一个过滤器。 常见过滤器 FilterSecurityInterceptor 是一个方法级的权限过滤器,基本位于过滤器链的最底部。 Excepti…...

Vue记事本应用实现教程
文章目录 1. 项目介绍2. 开发环境准备3. 设计应用界面4. 创建Vue实例和数据模型5. 实现记事本功能5.1 添加新记事项5.2 删除记事项5.3 清空所有记事 6. 添加样式7. 功能扩展:显示创建时间8. 功能扩展:记事项搜索9. 完整代码10. Vue知识点解析10.1 数据绑…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

ubuntu搭建nfs服务centos挂载访问
在Ubuntu上设置NFS服务器 在Ubuntu上,你可以使用apt包管理器来安装NFS服务器。打开终端并运行: sudo apt update sudo apt install nfs-kernel-server创建共享目录 创建一个目录用于共享,例如/shared: sudo mkdir /shared sud…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

日常一水C
多态 言简意赅:就是一个对象面对同一事件时做出的不同反应 而之前的继承中说过,当子类和父类的函数名相同时,会隐藏父类的同名函数转而调用子类的同名函数,如果要调用父类的同名函数,那么就需要对父类进行引用&#…...
