代码随想录算法训练营DAY45|C++动态规划Part7|70.爬楼梯(进阶版)、322. 零钱兑换、279.完全平方数
文章目录
- 70.爬楼梯(进阶版)
- ⭐️322. 零钱兑换
- 思路
- CPP代码
- 总结
- 279.完全平方数
- 思路
- CPP代码
70.爬楼梯(进阶版)
卡码网:57. 爬楼梯
文章讲解:70.爬楼梯(进阶版)
本题就是典型了完全背包排列问题,也没有什么绕弯,比较简单
#include <bits/stdc++.h>
using namespace std;int main () {int m, n;cin >> n >> m;std::vector<int> dp(n + 1, 0);dp[0] = 1;for (int j = 1; j <= n; j++) {for (int i = 0; i <= m; i++) {if (j >= i)dp[j] += dp[j - i]; }}cout << dp[n] << endl;return 0;
}
⭐️322. 零钱兑换
力扣题目链接
文章讲解:322. 零钱兑换
视频讲解:装满背包最少的物品件数是多少?| LeetCode:322.零钱兑换
在这里,我先总结一下之前写过的题目
在518.零钱兑换II中,我们求的是装满这个背包有多少种办法,求的是不强调元素顺序的组合数,递推公式是dp[j]+=dp[j-coins[i]]
在377. 组合总和 Ⅳ中,我们也求的是装满这个背包有多少种方法,但是求的是强调元素顺序的排列数,递推公式也是dp[j]+=dp[j-coins[i]],但是我们的遍历顺序是外层for遍历背包,内层for循环遍历物品
本题中,我们求的是装满这个背包最少用多少件物品
思路
- 确定dp数组的含义
本题中要装满容量为account的背包,最少的物品。那么很直观我们的dp数组的含义就是装满容量为j的背包,所需要的最少物品数量为dp[j]
- 递推公式
首先我们放物品应该如何表达?
如果我们要装满一个j-coins(i)容量大背包,所需要的最少物品为dp[j-coins(i)],那我现在要装一个j容量的背包,dp[j]可以有一种取值是dp[j] = dp[j-coins(i)]+1(因为我们在遍历coins[i]),那现在我要求一个装满j容量的最小值,那肯定就是
d p [ j ] = m i n ( d p [ j − c o i n s ( i ) ] + 1 , d p [ j ] ) dp[j] = min(dp[j-coins(i)]+1, dp[j]) dp[j]=min(dp[j−coins(i)]+1,dp[j])
- 初始化
聊到初始化,我们首先就要像dp[0]等于多少,很明显,根据题目含义,account=0的话,我们什么都不放就可以凑成这个account了。
之前我们把非0下标的值初始成0是为了防止我们在递推公式求的值被初始值覆盖,因为我们之前都是dp=max(...),但是在本题中,我们的递推公式出现的是dp[j]=min(...),所以我们应该把非零下标初始成INT_MAX。这样我们在推导赋值的时候才不会被初始值给覆盖掉
- 遍历顺序
还记得377. 组合总和 Ⅳ这篇文章遍历顺序部分,我们做了一个小总结,先遍历物品在遍历背包求的是组合数;先遍历背包再遍历物品求的就是排列数。
在本题中,我们求的是最少物品是多少,所以本题和组合排列没什么关系,不影响我们最终要求的最少的元素数量,故本题什么样的遍历顺序都可以。
- 打印
以输入:coins = [1, 2, 5], amount = 5为例 dp[amount]为最终结果。

CPP代码
// 版本一 先物品,再背包
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0;for (int i = 0; i < coins.size(); i++) { // 遍历物品for (int j = coins[i]; j <= amount; j++) { // 遍历背包if (dp[j - coins[i]] != INT_MAX) { // 如果dp[j - coins[i]]是初始值则跳过dp[j] = min(dp[j - coins[i]] + 1, dp[j]);}}}if (dp[amount] == INT_MAX) return -1;return dp[amount];}
};// 版本二 先背包,再物品
class Solution {
public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount + 1, INT_MAX);dp[0] = 0;for (int i = 1; i <= amount; i++) { // 遍历背包for (int j = 0; j < coins.size(); j++) { // 遍历物品if (i - coins[j] >= 0 && dp[i - coins[j]] != INT_MAX ) {dp[i] = min(dp[i - coins[j]] + 1, dp[i]);}}}if (dp[amount] == INT_MAX) return -1;return dp[amount];}
};
- 时间复杂度: O(n * amount),其中 n 为 coins 的长度
- 空间复杂度: O(amount)
总结
装满背包最少要多少物品 的递推公式要重点关注,再一个就是关于初始值的设定也很有讲究。
279.完全平方数
力扣题目链接
视频讲解:换汤不换药!| LeetCode:279.完全平方数
文章讲解:279.完全平方数
状态:典型的背包问题!真的就是换汤不换药
很明显,我们这里的n就是我们的背包容量,然后物品的重量和价值就是各个完全平方数,题目中要求的是用完全平方数拼凑出n的最小个数,这不就是妥妥的上一题
322.零钱兑换的思路?也就是说求的是装满这个背包所需要的最少物品的数量
思路
- dp数组的含义
看完上面对题目的论述,本题直接j表示背包容量,dp[j]表示能装满背包所需要的最少物品。
- 递归函数
跟上一题一样,直接是dp[j] = min(dp[j - i * i] + 1, dp[j])
- 初始化
dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。
同理,从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j])中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值INT_MAX,这样dp[j]在递推的时候才不会被初始值覆盖。
- 遍历顺序
与上一题一样,本题外层for遍历背包,内层for遍历物品,还是外层for遍历物品,内层for遍历背包,都是可以的!
- 打印
略
CPP代码
// 版本一
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for (int i = 0; i <= n; i++) { // 遍历背包for (int j = 1; j * j <= i; j++) { // 遍历物品dp[i] = min(dp[i - j * j] + 1, dp[i]);}}return dp[n];}
};// 版本二
class Solution {
public:int numSquares(int n) {vector<int> dp(n + 1, INT_MAX);dp[0] = 0;for (int i = 1; i * i <= n; i++) { // 遍历物品for (int j = i * i; j <= n; j++) { // 遍历背包dp[j] = min(dp[j - i * i] + 1, dp[j]);}}return dp[n];}
};
- 时间复杂度: O(n * √n)
- 空间复杂度: O(n)
相关文章:

代码随想录算法训练营DAY45|C++动态规划Part7|70.爬楼梯(进阶版)、322. 零钱兑换、279.完全平方数
文章目录 70.爬楼梯(进阶版)⭐️322. 零钱兑换思路CPP代码总结 279.完全平方数思路CPP代码 70.爬楼梯(进阶版) 卡码网:57. 爬楼梯 文章讲解:70.爬楼梯(进阶版) 本题就是典型了完全背包排列问题,…...

Linux(openEuler、CentOS8)企业内网DHCP服务器搭建(固定Mac获取指定IP)
----本实验环境为openEuler系统<以server方式安装>(CentOS8基本一致,可参考本文)---- 目录 一、知识点二、实验(一)为服务器配置网卡和IP(二)为服务器安装DHCP服务软件(三&a…...

c#读取hex文件方法,相对来说比较清楚
Hex文件解读_c#读取hex文件-CSDN博客 https://wenku.csdn.net/answer/d67f30cf834c435ca37c3d1ef5e78a62?ops_request_misc%257B%2522request%255Fid%2522%253A%2522171498156816800227423661%2522%252C%2522scm%2522%253A%252220140713.130102334.pc%255Fall.%2522%257D&…...
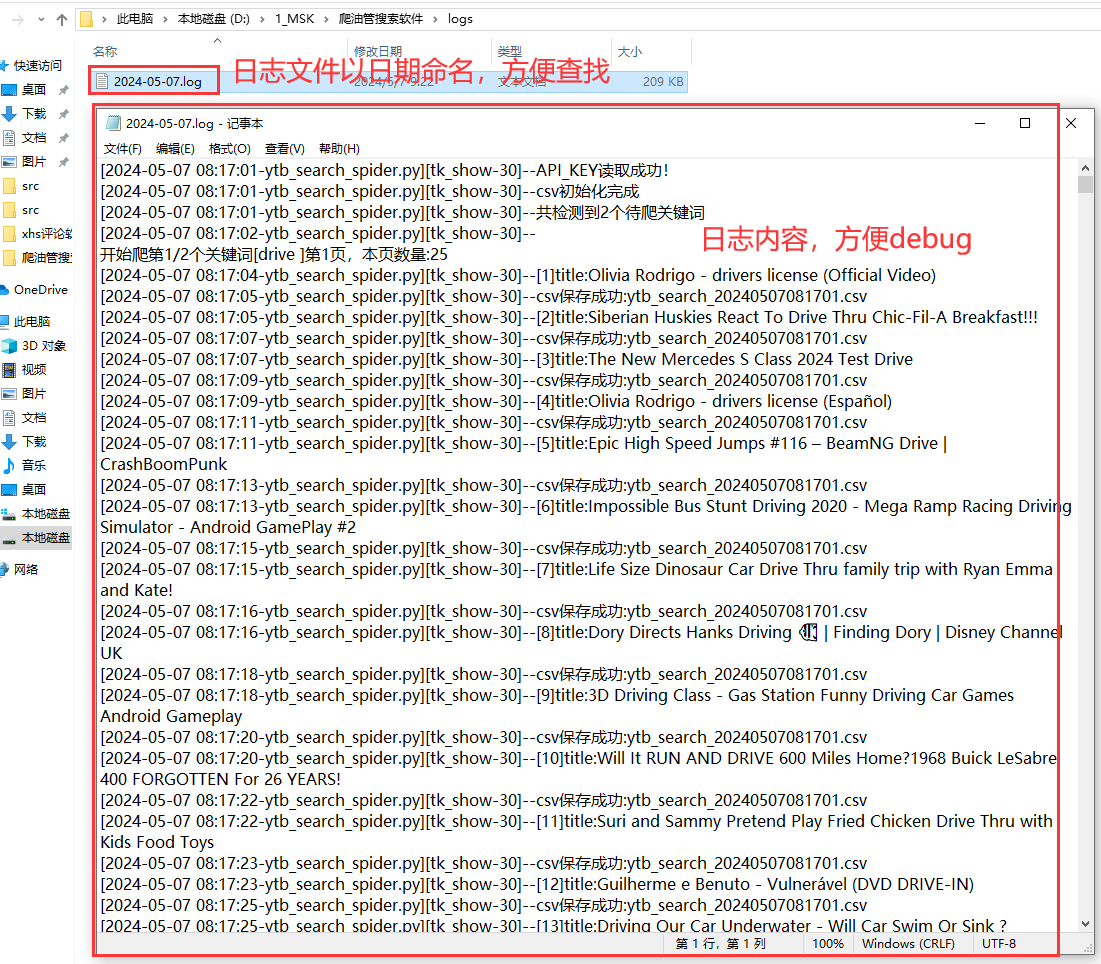
【ytb数据采集器】按关键词批量爬取视频数据,界面软件更适合文科生!
一、背景介绍 1.1 爬取目标 用Python独立开发的爬虫工具,作用是:通过搜索关键词采集油管的搜索结果,包含14个关键字段:关键词,页码,视频标题,视频id,视频链接,发布时间,视频时长,频道名称,频道id,频道链接,播放数,点赞数,评论数…...

三条命令快速配置Hugging Face
大家好啊,我是董董灿。 本文给出一个配置Hugging Face的方法,让你在国内可快速从Hugging Face上下在模型和各种文件。 1. 什么是 Hugging Face Hugging Face 本身是一家科技公司,专注于自然语言处理(NLP)和机器学习…...

Python网络编程 03 实验:FTP详解
文章目录 一、小实验FTP程序需求二、项目文件架构三、服务端1、conf/settings.py2、conf/accounts.cgf3、conf/STATUS_CODE.py4、启动文件 bin/ftp_server.py5、core/main.py6、core/server.py 四、客户端1、conf/STATUS_CODE.py2、bin/ftp_client.py 五、在终端操作示例 一、小…...
)
个人银行账户管理程序(2)
在(1)的基础上进行改进 1:增加一个静态成员函数total,记录账户总金额和静态成员函数getTotal 2对不需要改变的对象进行const修饰 3多文件实现 account。h文件 #ifndef _ACCOUNT_ #define _ACCOUNT_ class SavingAccount {pri…...

2024.04.19校招 实习 内推 面经
绿*泡*泡VX: neituijunsir 交流*裙 ,内推/实习/校招汇总表格 1、校招&转正实习 | 美团无人机业务部招聘(内推) 校招&转正实习 | 美团无人机业务部招聘(内推) 2、校招&实习 | 快手 这些岗位…...

Python并发编程 04 进程与线程基础
文章目录 一、操作系统简介二、进程三、线程四、线程的调用1、示例2、join方法3、setDaemon方法4、继承式调用(不推荐)5、其他方法 一、操作系统简介 ①操作系统是一个用来协调、管理和控制计算机硬件和软件资源的系统程序,它位于硬件和应用…...
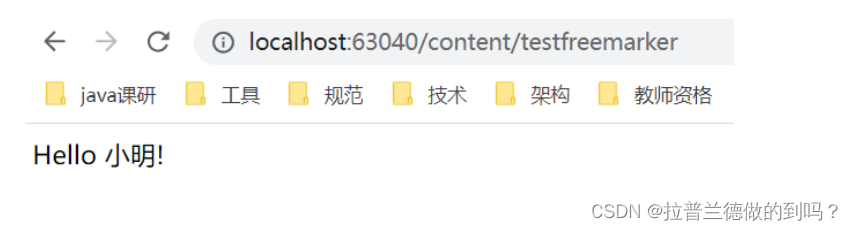
模板引擎Freemarker
什么是模板引擎 根据前边的数据模型分析,课程预览就是把课程的相关信息进行整合,在课程预览界面进行展示,课程预览界面与课程发布的课程详情界面一致。 项目采用模板引擎技术实现课程预览界面。什么是模板引擎? 早期我们采用的…...

刷题训练之模拟
> 作者:დ旧言~ > 座右铭:松树千年终是朽,槿花一日自为荣。 > 目标:熟练掌握模拟算法。 > 毒鸡汤:学习,学习,再学习 ! 学,然后知不足。 > 专栏选自:刷题训…...

视频监控平台:交通运输标准JTT808设备SDK接入源代码函数分享
目录 一、JT/T 808标准简介 (一)概述 (二)协议特点 1、通信方式 2、鉴权机制 3、消息分类 (三)协议主要内容 1、位置信息 2、报警信息 3、车辆控制 4、数据转发 二、代码和解释 (一…...
)
【C++】多态 — 多态的细节补充(下篇)
前言: 我们学习了多态的形式和如何使用多态,这一章我们将来讲一讲多态的原理… 目录 动态绑定与静态绑定: 动态绑定与静态绑定: 静态绑定又称为前期绑定(早绑定),在程序编译期间确定了程序的行为,也称为静态多态,比如…...
系统安全与应用【2】
1.开关机安全控制 1.1 GRUB限制 限制更改GRUB引导参数 通常情况下在系统开机进入GRUB菜单时,按e键可以查看并修改GRUB引导参数,这对服务器是一个极大的威胁。可以为GRUB 菜单设置一个密码,只有提供正确的密码才被允许修改引导参数。 实例&…...
EtherCAT总线速度轴控制功能块(COSESYS ST源代码)
测试环境为汇川PLC,型号 AM402-CPU1608TP、伺服驱动器为禾川X3E,具体通信配置可以参考下面文章链接: 1、使能和点动控制 汇川AM400PLC通过EtherCAT总线控制禾川X3E伺服使能和点动控制-CSDN博客文章浏览阅读31次。进行通信之前需要安装禾川X3E的XML文件,具体方法如下:1、汇…...

【码银送书第十九期】《图算法:行业应用与实践》
作者:嬴图团队 01 前言 在当今工业领域,图思维方式与图数据技术的应用日益广泛,成为图数据探索、挖掘与应用的坚实基础。本文旨在分享嬴图团队在算法实践应用中的宝贵经验与深刻思考,不仅促进业界爱好者之间的交流,…...
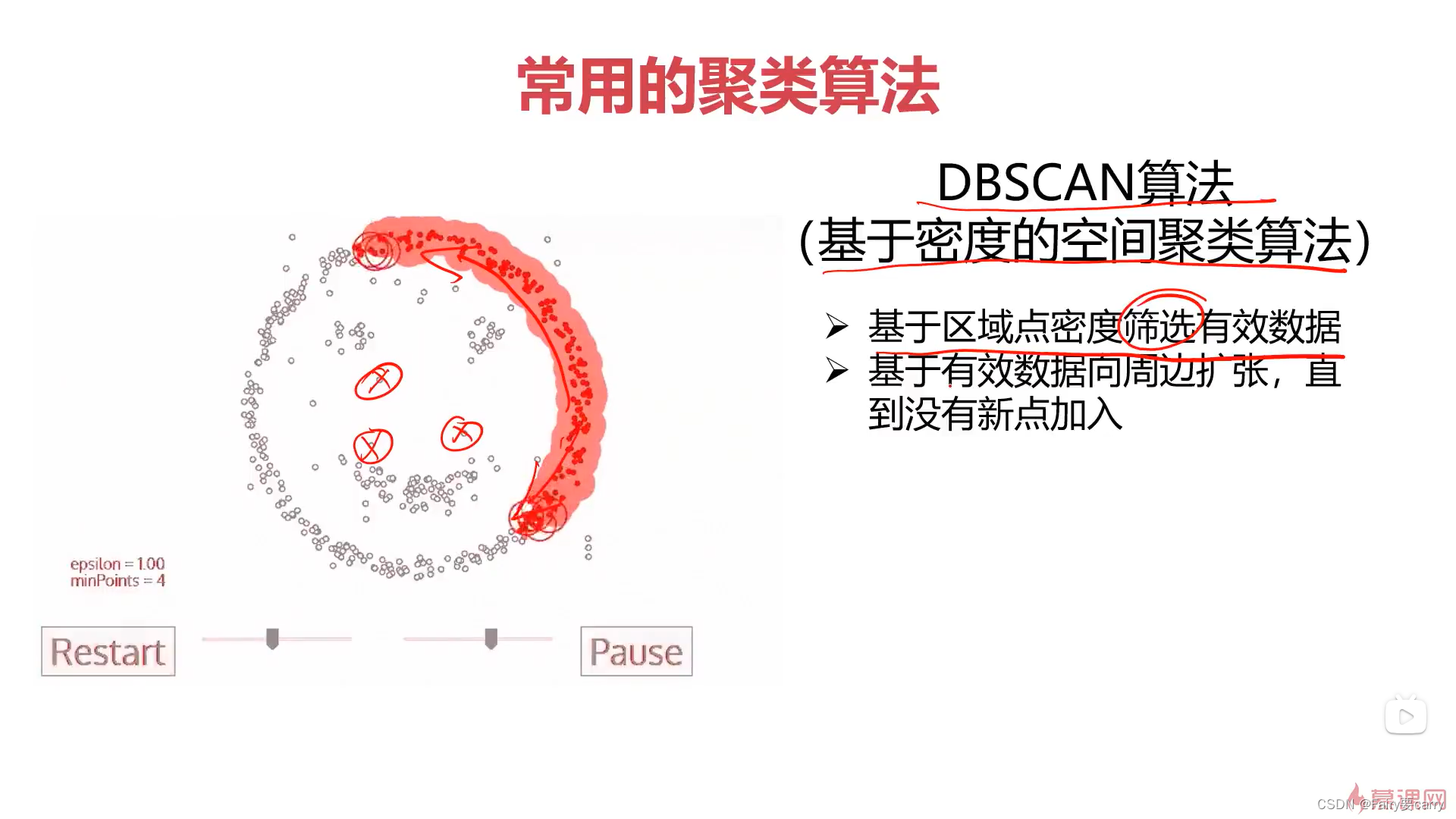
无监督式学习
1.是什么? 无监督式学习与监督式学习**最大的区别就是:**没有事先给定的训练实例,它是自动对输入的示例进行分类或者分群; 优点:不需要标签数据,极大程度上扩大了我们的数据样本,其次不受监督信…...

docker 安装镜像及使用命令
目录 1. Mysql2. Redis3. Nginx4. Elasticsearch官网指导 docker pull 容器名:版本号 拉取容器, 不指定版本号默认最新的 run 运行 -d 后台运行 -p 3306:3306 -p是port 对外端口:对内端口 –name xyy_mysql 容器名称 -e MYSQL_ROOT_PASSWORD123456 环境变量 -v 系统地址:docker…...

Python运维之多进程!!
本节的快速导航目录如下喔!!! 一、创建进程的类Process 二、进程并发控制之Semaphore 三、进程同步之Lock 四、进程同步之Event 五、进程优先队列Queue 六、多进程之进程池Pool 七、多进程之数据交换Pipe 一、创建进程的类Process mu…...

Redis(无中心化集群搭建)
文章目录 1.无中心化集群1.基本介绍2.集群说明 2.基本环境搭建1.部署规划(6台服务器)2.首先删除上次的rdb和aof文件(对之前的三台服务器都操作)1.首先分别登录命令行,关闭redis2.清除/root/下的rdb和aof文件3.把上次的…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

tauri项目,如何在rust端读取电脑环境变量
如果想在前端通过调用来获取环境变量的值,可以通过标准的依赖: std::env::var(name).ok() 想在前端通过调用来获取,可以写一个command函数: #[tauri::command] pub fn get_env_var(name: String) -> Result<String, Stri…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...
