插值多项式的龙格现象的介绍与模拟
在文章拉格朗日插值多项式的原理介绍及其应用中,笔者介绍了如何使用拉格朗日插值多项式来拟合任意数据点集。
事实上,插值多项式会更倾向于某些形状。德国数学家卡尔·龙格Carl Runge发现,插值多项式在差值区间的端点附近会发生扭动,且波动较大。这就是数值分析中著名的龙格现象(Runge Phenomenon)。
本文以函数f(x)=11+12x2f(x)=\frac{1}{1+12x^{2}}f(x)=1+12x21和区间[-1,1]为例,在该区间上平均取n个点(包括端点),在函数图像上得到n个样本点,对这些样本点使用拉格朗日插值多项式,并绘制该插值多项式的图像,观察其在端点附近的表现。
Python实现程序如下:
# -*- coding: utf-8 -*-
# @Time : 2023/3/8 18:55
# @Author : Jclian91
# @File : runge_phenomenon.py
# @Place : Xuhui, Shanghai
import matplotlib.pyplot as plt# sample function
# 函数f(x)=1/(1+12*x**2)
def sample_func(x):return 1 / (1 + 12 * x ** 2)# get sample points from sample function with interval [-1, 1]
def get_sample_points(n):# n: number of sample pointsstep = 2 / (n-1)x_values = [-1 + i * step for i in range(n)]y_values = [sample_func(x) for x in x_values]return x_values, y_values# get basic lagrange polynomial unit
def get_lagrange_polynomial_unit(x_values, k, x):# x_values: values of x in list x_values# k: kth lagrange polynomial unit# x: variable in kth lagrange polynomial unitpoly_unit = 1for i in range(len(x_values)):if i != k:poly_unit *= (x-x_values[i])/(x_values[k]-x_values[i])return poly_unit# get lagrange polynomial
def get_lagrange_polynomial(x_values, y_values, x):poly = 0for i, y in enumerate(y_values):poly += y * get_lagrange_polynomial_unit(x_values, i, x)return poly# plot curves with matplotlib
def plot_function(n):# plot lagrange polynomial with n sample points from sample functionsample_x_values, sample_y_values = get_sample_points(n)sample_points_number = 500x_list = [-1 + i * 2 / (sample_points_number-1) for i in range(sample_points_number)]original_y_list = [sample_func(x) for x in x_list]y_list = [get_lagrange_polynomial(sample_x_values, sample_y_values, x)for x in x_list]plt.plot(x_list, original_y_list, label='f(x)=1/(1+12*x**2)')plt.plot(x_list, y_list, label='lagrange polynomial')plt.title(f'Runge phenomenon with {n} basic points in function f(x)=1/(1+12*x**2)')plt.legend()# plt.show()plt.savefig(f"{n}_basic_points.png")if __name__ == '__main__':n_points = 5plot_function(n_points)
当n=5时,拉格朗日插值多项式的图像如下:

当n=15,拉格朗日插值多项式的图像如下:

当n=25时,拉格朗日插值多项式的图像如下:

当n=35时,拉格朗日插值多项式的图像如下:

当n=45时,拉格朗日插值多项式的图像如下:

通过上述程序的模拟结果,我们可以发现该插值多项式在区间端点附近会发生扭动,当n越大,扭动的幅度就越大,这是用计算机程序对龙格现象的一个模拟。
相关文章:

插值多项式的龙格现象的介绍与模拟
在文章拉格朗日插值多项式的原理介绍及其应用中,笔者介绍了如何使用拉格朗日插值多项式来拟合任意数据点集。 事实上,插值多项式会更倾向于某些形状。德国数学家卡尔龙格Carl Runge发现,插值多项式在差值区间的端点附近会发生扭动&#x…...
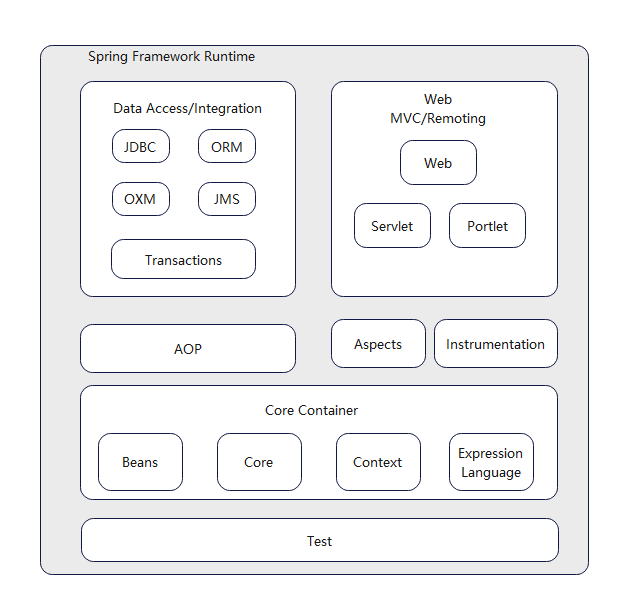
Spring整体架构包含哪些组件?
Spring是一个轻量级java开源框架。Spring是为了解决企业应用开发的复杂性而创建的,它使用基本的JavaBean来完成以前只可能由EJB完成的事情。 Spring的用途不仅限于服务器端的开发,从简单性、可测试性和松耦合的角度而言,任何java应用都可以从…...

开发接口需要考虑哪些问题?
1 接口名字 user/ user/adduser/xxx 见名知意,调用接口的开发人员和后来接手的开发人员能够根据接口名称大致猜测出接口作用。 2 协议 设计接口时,应明确调用接口的协议,是采用HTTP协议,HTTPS协议还是FTP协议。比如跨语言调用通常使用WebS…...

关于Activiti7审批工作流绘画流程图(2)
文章目录一、25张表详解二、安装插件一.定制流程提示:以下是本篇文章正文内容,下面案例可供参考 一、25张表详解 虽然表很多,但是仔细观察,我们会发现Activiti 使用到的表都是 ACT_ 开头的。表名的第二部分用两个字母表明表的用…...
对日期进行格式化)
String.format()对日期进行格式化
前言:String.format()作为文本处理工具,为我们提供强大而丰富的字符串格式化功能,这里根据查阅的资料做个学习笔记,整理成如下文章,供后续复习查阅。一. format()方法的两种重载形式:format(String format,…...

核酸检测信息管理系统
目录前言一、功能与需求分析二、详细设计与实现1、data包(1)DataDataBase(2)NaPaNamePassword2、operation包(1)操作接口(2)Resident用户功能(3)Simper用户功…...

典型回溯题目 - 全排列(一、二)
典型回溯题目 - 全排列(一、二) 46. 全排列 题目链接:46. 全排列状 题目大意: 给定一个不含重复数字的数组 nums ,返回其 所有可能的全排列 。你可以 按任意顺序 返回答案。 注意:(1…...

数据清洗和特征选择
数据清洗和特征选择 数据清洗和特征挖掘的工作是在灰色框中框出的部分,即“数据清洗>特征,标注数据生成>模型学习>模型应用”中的前两个步骤。 灰色框中蓝色箭头对应的是离线处理部分。主要工作是 从原始数据,如文本、图像或者应…...

java StringBuilder 和 StringBuffer 万字详解(深度讲解)
StringBuffer类介绍和溯源StringBuffer类常用构造器和常用方法StringBuffer类 VS String类(重要)二者的本质区别(含内存图解)二者的相互转化StringBuilder类介绍和溯源StringBuilder类常用构造器和常用方法String类,St…...
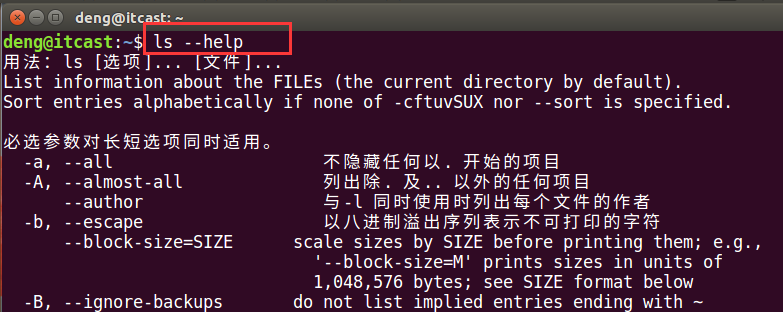
【Linux】帮助文档查看方法
目录1 Linux帮助文档查看方法1.1 man1.2 内建命令(help)1 Linux帮助文档查看方法 1.1 man man 是 Linux 提供的一个手册,包含了绝大部分的命令、函数使用说明。 该手册分成很多章节(section),使用 man 时可以指定不同的章节来浏…...
 HelloWorld 之一 helloworld及.inf文件)
UEFI 实战(2) HelloWorld 之一 helloworld及.inf文件
初识UEFI 按惯例,首先让我们用HelloWorld跟UEFI打个招呼吧 标准application /*main.c */ #include <Uefi.h> EFI_STATUS UefiMain ( IN EFI_HANDLE ImageHandle, IN EFI_SYSTEM_TABLE *SystemTable ) { SystemTable -> ConOut-> OutputString(SystemTab…...
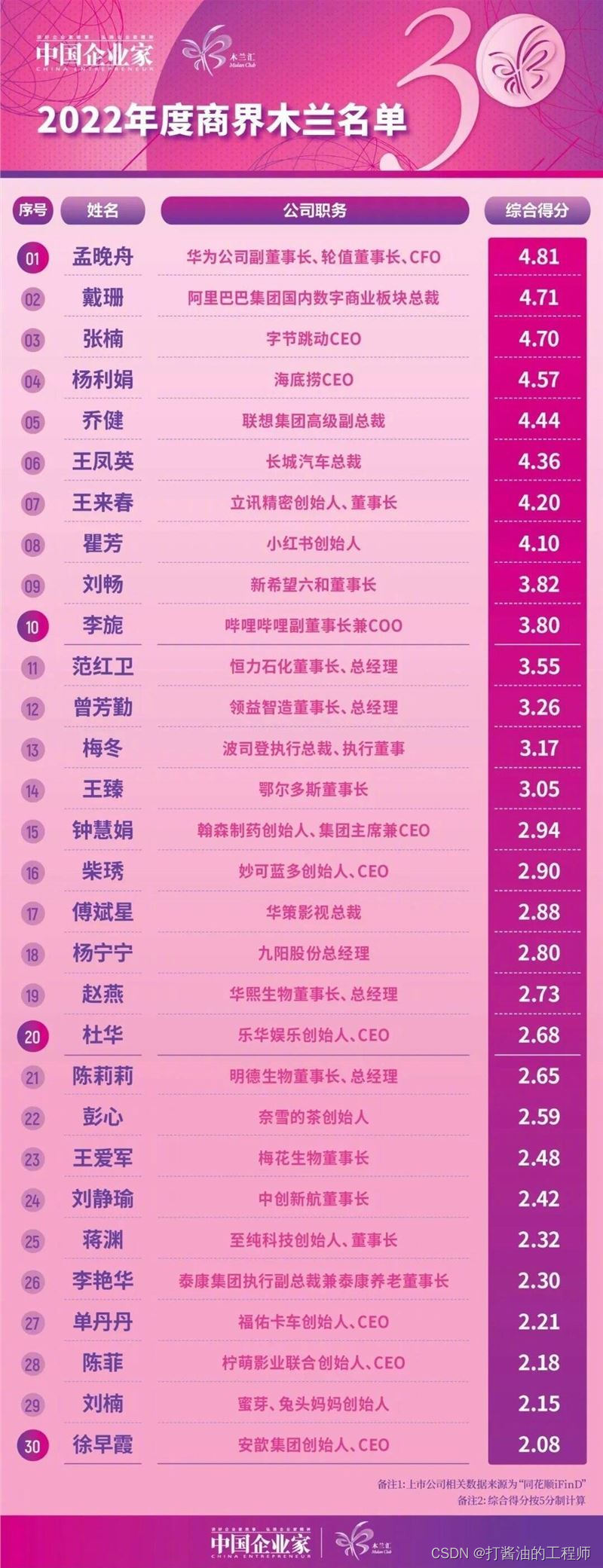
向2022年度商界木兰上榜女性致敬!
目录 信息来源: 2022年度商界木兰名单 简介 评选标准 动态 榜单 为你心中的2023商界女神投上一票 信息来源: 2022年度商界木兰榜公布 华为孟晚舟获商界木兰最高分 - 脉脉 【最具影响力女性】历届商界木兰榜单 中国最具影响力的30位商界女性名单…...

ChatGPT助力校招----面试问题分享(二)
1 ChatGPT每日一题:DC-DC与LDO的区别 问题:介绍一下DC-DC与LDO的区别 ChatGPT:DC-DC和LDO都是电源管理电路,它们的主要作用是将输入电压转换为所需的输出电压,以供电子设备使用。但是,它们之间存在一些重…...
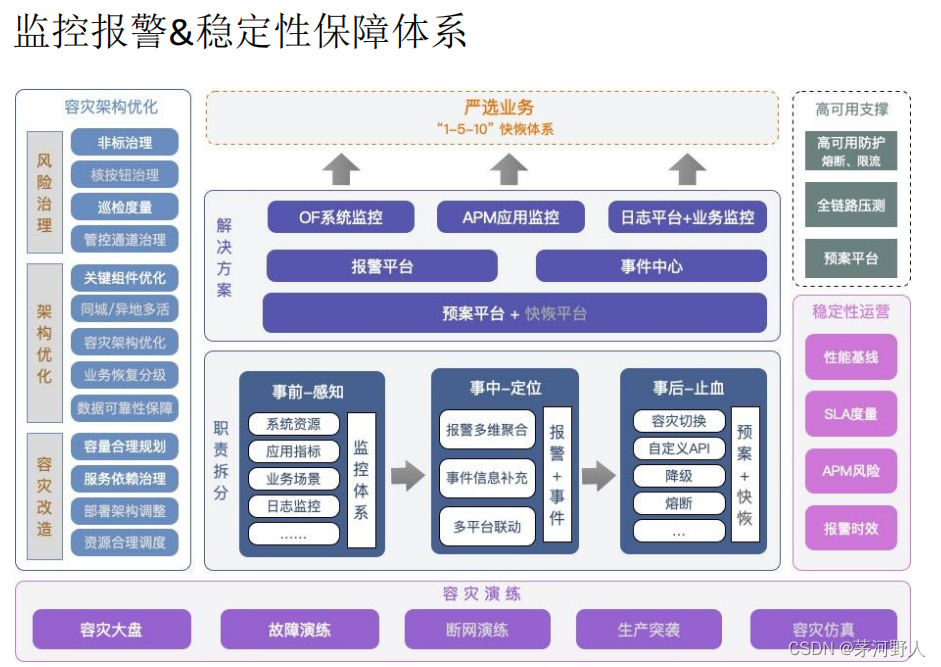
JAVA架构与开发(JAVA架构是需要考虑的几个问题)
在企业中JAVA架构师主要负责企业项目技术架构,企业技术战略制定,技术框架搭建,技术培训和技术攻坚的工作。 在JAVA领域,比较多的都是web项目。用于解决企业的数字化转型。对于JAVA架构师而言,平时对项目的架构主要考虑…...

vue 中 v-for 的使用
v-for 获取列表的前 n 条、中间范围、末尾 n 条的数据 list: [{ img: /static/home/news1.png, title: 标题1 },{ img: /static/home/news2.png, title: 标题2 },{ img: /static/home/news1.png, title: 标题3 },{ img: /static/home/news2.png, title: 标题4 },{ img: /stati…...

项目--基于RTSP协议的简易服务器开发(2)
一、项目创立初衷: 由于之前学过计算机网络的相关知识,了解了计算机网络的基本工作原理,对于主流的协议有一定的了解。但对于应用层的协议还知之甚少,因此我去了解了下目前主要的应用层传输协议,发现RTSP(…...
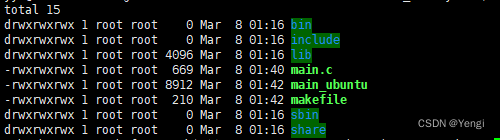
ubus编译_环境搭建
文章目录一、环境搭建脚本toolChain_jsonc.cmaketoolChain_libubox.cmaketoolChain_ubus.cmakeinstall.sh二、测试出现问题:三、测试uloopmain.c 每5s打印信息一、环境搭建脚本 准备四个文件 install.sh,toolChain_jsonc.cmake,toolChain_libubox.cmake,toolChai…...

移动通信(16)信号检测
常见的信号检测算法一般包括以下几类检测算法:最优、线性和非线性。最优检测算法:最大似然算法线性检测算法:迫零检测算法和最小均方误差检测算法非线性检测算法:串行干扰消除检测算法球形译码检测算法属于一种次优检测算法&#…...
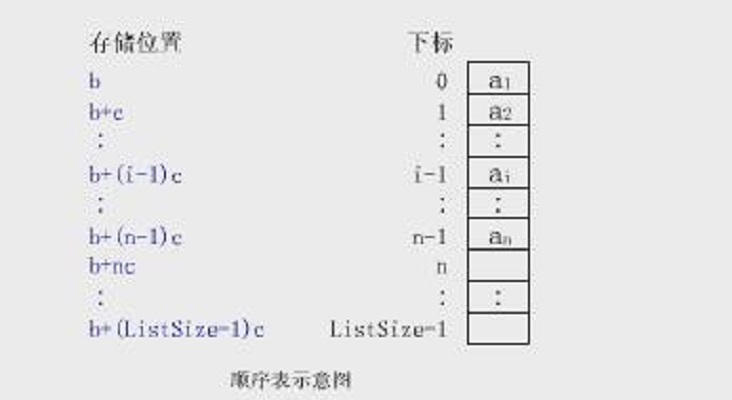
数据结构与算法之《顺序表》
目录 1.什么是顺序表 顺序表的优势和缺点 顺序表预备知识 顺序表的代码实现 顺序表头部插入 顺序表的销毁 顺序表的头删 顺序表的尾删 顺序表的尾插 顺序表的任意位置插入 顺序表的查找 顺序表的打印 1.什么是顺序表 这篇文章我们来讲一下基础数据结构的顺序表&…...

MySQL索引15连问,抗住!
1. 索引是什么?索引是一种能提高数据库查询效率的数据结构。它可以比作一本字典的目录,可以帮你快速找到对应的记录。索引一般存储在磁盘的文件中,它是占用物理空间的。正所谓水能载舟,也能覆舟。适当的索引能提高查询效率&#x…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

【力扣数据库知识手册笔记】索引
索引 索引的优缺点 优点1. 通过创建唯一性索引,可以保证数据库表中每一行数据的唯一性。2. 可以加快数据的检索速度(创建索引的主要原因)。3. 可以加速表和表之间的连接,实现数据的参考完整性。4. 可以在查询过程中,…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

安宝特方案丨船舶智造的“AR+AI+作业标准化管理解决方案”(装配)
船舶制造装配管理现状:装配工作依赖人工经验,装配工人凭借长期实践积累的操作技巧完成零部件组装。企业通常制定了装配作业指导书,但在实际执行中,工人对指导书的理解和遵循程度参差不齐。 船舶装配过程中的挑战与需求 挑战 (1…...

vulnyx Blogger writeup
信息收集 arp-scan nmap 获取userFlag 上web看看 一个默认的页面,gobuster扫一下目录 可以看到扫出的目录中得到了一个有价值的目录/wordpress,说明目标所使用的cms是wordpress,访问http://192.168.43.213/wordpress/然后查看源码能看到 这…...
