c++ 归并排序
归并排序是一种遵循分而治之方法的排序算法。它的工作原理是递归地将输入数组划分为较小的子数组并对这些子数组进行排序,然后将它们合并在一起以获得排序后的数组。
简单来说,归并排序的过程就是将数组分成两半,对每一半进行排序,然后将已排序的两半合并在一起。重复这个过程,直到整个数组排序完毕。

归并排序算法
归并排序是如何工作的?
归并排序是一种流行的排序算法,以其高效和稳定而闻名。它遵循分而治之的方法对给定的元素数组进行排序。
以下是合并排序如何工作的分步说明:
1、划分:递归地将列表或数组划分为两半,直到不能再划分为止。
2、征服:使用合并排序算法对每个子数组进行单独排序。
3、合并:已排序的子数组按排序顺序合并在一起。该过程将继续,直到两个子数组中的所有元素都已合并。
归并排序示意图:
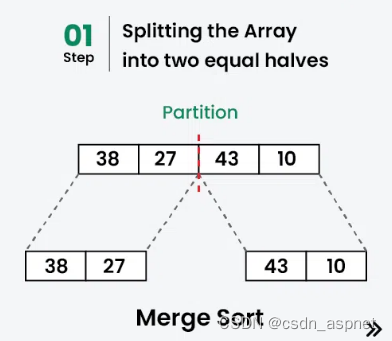
让我们使用归并排序对数组或列表[38, 27, 43, 10]进行排序

让我们看看上面例子的工作原理:
划分:
[38, 27, 43, 10]分为[38, 27 ] 和[43, 10]。
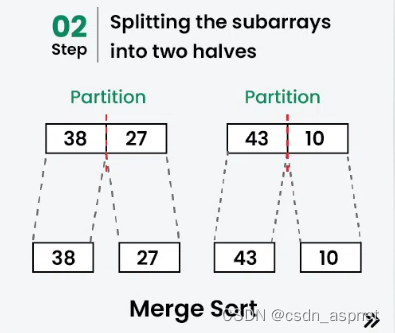
[38, 27]分为[38]和[27]。
[43, 10]分为[43]和[10]。
征服:
[38]已经排序。
[27]已经排序。
[43]已经排序。
[10]已经排序。
合并:
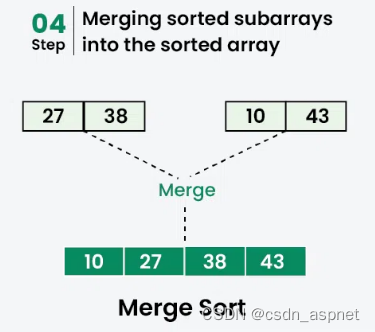
合并[38]和[27]得到[27, 38]。
合并[43]和[10]得到[10,43]。
合并[27, 38]和[10,43]得到最终的排序列表[10, 27, 38, 43]
因此,排序列表为[10, 27, 38, 43]。
归并排序的实现:
// C++ program for Merge Sort
#include <bits/stdc++.h>
using namespace std;
// Merges two subarrays of array[].
// First subarray is arr[begin..mid]
// Second subarray is arr[mid+1..end]
void merge(int array[], int const left, int const mid,
int const right)
{
int const subArrayOne = mid - left + 1;
int const subArrayTwo = right - mid;
// Create temp arrays
auto *leftArray = new int[subArrayOne],
*rightArray = new int[subArrayTwo];
// Copy data to temp arrays leftArray[] and rightArray[]
for (auto i = 0; i < subArrayOne; i++)
leftArray[i] = array[left + i];
for (auto j = 0; j < subArrayTwo; j++)
rightArray[j] = array[mid + 1 + j];
auto indexOfSubArrayOne = 0, indexOfSubArrayTwo = 0;
int indexOfMergedArray = left;
// Merge the temp arrays back into array[left..right]
while (indexOfSubArrayOne < subArrayOne
&& indexOfSubArrayTwo < subArrayTwo) {
if (leftArray[indexOfSubArrayOne]
<= rightArray[indexOfSubArrayTwo]) {
array[indexOfMergedArray]
= leftArray[indexOfSubArrayOne];
indexOfSubArrayOne++;
}
else {
array[indexOfMergedArray]
= rightArray[indexOfSubArrayTwo];
indexOfSubArrayTwo++;
}
indexOfMergedArray++;
}
// Copy the remaining elements of
// left[], if there are any
while (indexOfSubArrayOne < subArrayOne) {
array[indexOfMergedArray]
= leftArray[indexOfSubArrayOne];
indexOfSubArrayOne++;
indexOfMergedArray++;
}
// Copy the remaining elements of
// right[], if there are any
while (indexOfSubArrayTwo < subArrayTwo) {
array[indexOfMergedArray]
= rightArray[indexOfSubArrayTwo];
indexOfSubArrayTwo++;
indexOfMergedArray++;
}
delete[] leftArray;
delete[] rightArray;
}
// begin is for left index and end is right index
// of the sub-array of arr to be sorted
void mergeSort(int array[], int const begin, int const end)
{
if (begin >= end)
return;
int mid = begin + (end - begin) / 2;
mergeSort(array, begin, mid);
mergeSort(array, mid + 1, end);
merge(array, begin, mid, end);
}
// UTILITY FUNCTIONS
// Function to print an array
void printArray(int A[], int size)
{
for (int i = 0; i < size; i++)
cout << A[i] << " ";
cout << endl;
}
// Driver code
int main()
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
int arr_size = sizeof(arr) / sizeof(arr[0]);
cout << "Given array is \n";
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
cout << "\nSorted array is \n";
printArray(arr, arr_size);
return 0;
}
// This code is contributed by Mayank Tyagi
// This code was revised by Joshua Estes
输出
给定数组是
12 11 13 5 6 7
排序后的数组是
5 6 7 11 12 13
归并排序的复杂度分析:
时间复杂度:
最佳情况: O(n log n),当数组已经排序或接近排序时。
平均情况: O(n log n),当数组随机排序时。
最坏情况: O(n log n),当数组按相反顺序排序时。
空间复杂度: O(n),合并时使用的临时数组需要额外的空间。
归并排序的优点:
稳定性:归并排序是一种稳定的排序算法,这意味着它保持输入数组中相等元素的相对顺序。
保证最坏情况下的性能:归并排序的最坏情况时间复杂度为O(N logN),这意味着即使在大型数据集上它也能表现良好。
易于实现:分而治之的方法很简单。
归并排序的缺点:
空间复杂度:归并排序在排序过程中需要额外的内存来存储合并后的子数组。
非就地:合并排序不是就地排序算法,这意味着它需要额外的内存来存储排序后的数据。这对于关注内存使用的应用程序来说可能是一个缺点。
归并排序的应用:
对大型数据集进行排序
外部排序(当数据集太大而无法容纳在内存中时)
反转计数(计算数组中反转的次数)
查找数组的中位数
相关文章:

c++ 归并排序
归并排序是一种遵循分而治之方法的排序算法。它的工作原理是递归地将输入数组划分为较小的子数组并对这些子数组进行排序,然后将它们合并在一起以获得排序后的数组。 简单来说,归并排序的过程就是将数组分成两半,对每一半进行排序,…...

基于vs和C#的WPF应用之动画3
注:1、在内部和外部使用缓动函数 <Grid.Resources> <PowerEase x:Key"powerease" Power"3" EasingMode"EaseInOut"/> </Grid.Resources> <DoubleAnimation EasingFunction"{StaticResource powerease}&quo…...

Python import 必看技巧:打造干净利落的代码结构
大家好,学习Python你肯定绕不过一个概念import,它是连接不同模块的桥梁,是实现代码复用和模块化的关键。本文将带你深入探索Python中import的原理,并分享一些实用的导入技巧。 1. import 原理 导入机制概述 在Python中,模块(module)是一种封装Python代码的方式,它允许…...
(Computer Vision))
计算机视觉(CV)(Computer Vision)
计算机视觉技术(Computer Vision),解决的是什么? 图片和视频是非结构化数据,机器如果要理解某一图片或视频表达的内容,是无法直接分析的,这种情况,就需要有计算机视觉技术ÿ…...
python:画折线图
import pandas as pd import matplotlib.pyplot as plt from matplotlib.font_manager import FontProperties# 设置新宋体字体的路径 font_path D:/reportlab/simsun/simsun.ttf# 加载新宋体字体 prop FontProperties(fnamefont_path)""" # 读取 xlsx 文件 d…...

Spring Data JPA 与 MyBatisPlus的比较
前言 JPA(Java Persistence API)和MyBatis Plus是两种不同的持久化框架,它们具有不同的特点和适用场景。 JPA是Java官方的持久化规范,它提供了一种基于对象的编程模型,可以通过注解或XML配置来实现对象与数据库的映射…...

【C++】STL-list的使用
目录 1、list的使用 1.1 list的构造 1.2 list的遍历 1.3 list capacity 1.4 list element access 1.5 容量相关 list是一个带头双向循环链表 1、list的使用 1.1 list的构造 1.2 list的遍历 list只有两种遍历方式,因为没有operator[] 因为list的双向链表&am…...
)
进度条(小程序)
缓冲区的概念 缓冲区是内存中的一个临时存储区域,用来存放输入或输出数据。在标准 I/O 库中,缓冲区的使用可以提高数据处理的效率。例如,当向终端输出文本时,字符通常存储在缓冲区中,直到缓冲区满或者遇到特定条件时才…...
PyCharm安装教程(超详细图文教程)
一、下载和安装 1.进入PyCharm官方下载,官网下载地址: https://www.jetbrains.com/pycharm/download/ 专业版安装插件放网盘了,网盘下载即可:itcxy.xyz/229.html2.安装 1.下载后找到PyCharm安装包,然后双击双击.ex…...

金蝶BI应收分析报表:关于应收,这样分析
这是一张出自奥威-金蝶BI方案的BI应收分析报表,是一张综合运用了筛选、内存计算等智能分析功能以及数据可视化图表打造而成的BI数据可视化分析报表,可以让企业运用决策层快速知道应收账款有多少?账龄如何?周转情况如何?…...
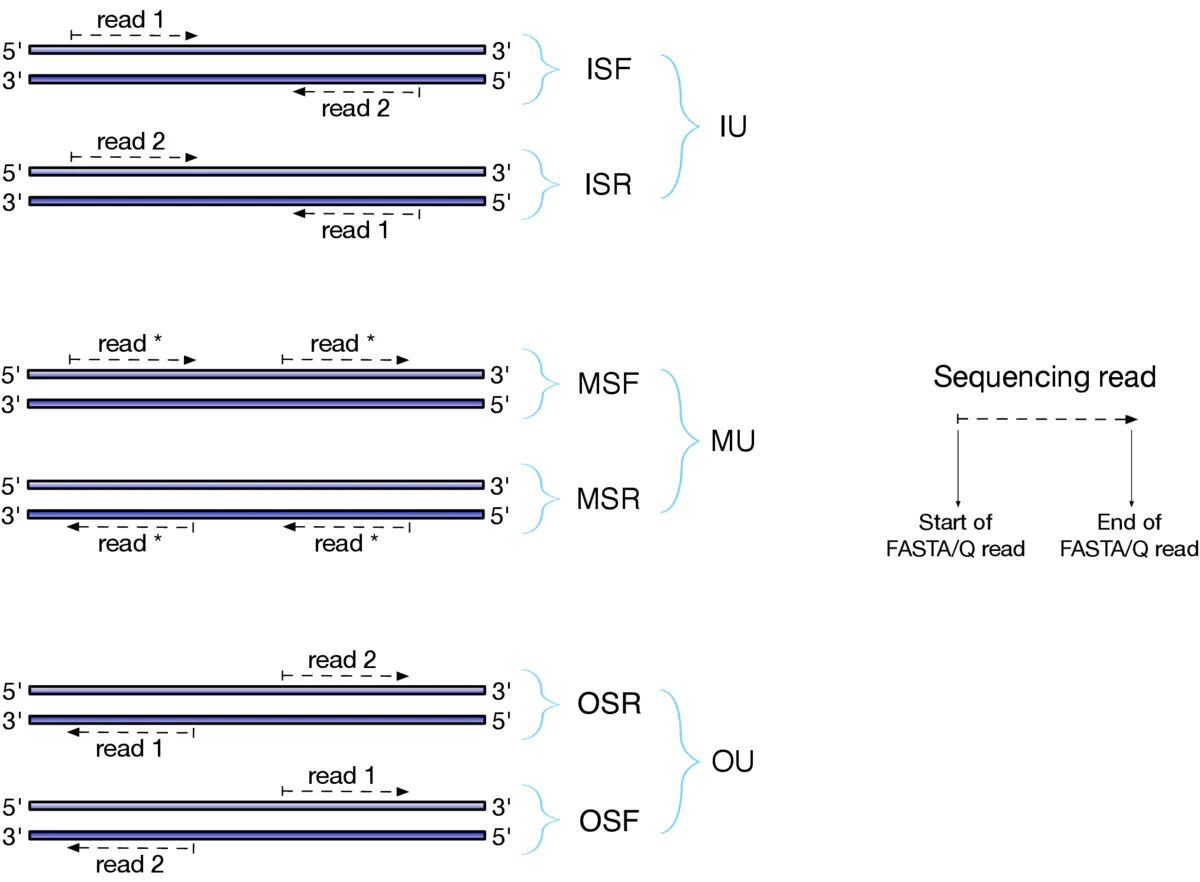
salmon使用体验
文章目录 salmon转录本定量brief模式一:fastq作为输入文件需要特别注意得地方 模式二: bam文件作为输入 salmon转录本定量 brief 第一点是,通常说的转录组分析其中有一项是转录本定量,这是一个很trick的说话,说成定量…...

Ubuntu 20.04 安装 Ansible
使用官方的 Ubuntu PPA 更新包列表: apt update安装软件属性常用命令 apt install software-properties-common添加 Ansible PPA 到系统: add-apt-repository --yes --update ppa:ansible/ansible再次更新包列表以包括新添加的 PPA: apt …...

TypeScript学习笔记:强类型JavaScript的优雅之旅
在前端开发领域,JavaScript以其灵活性和广泛的支持度成为无可争议的王者。然而,随着项目规模的增长,JavaScript的动态类型特性开始暴露出一些问题,比如代码的可维护性、类型错误难以提前发现等。为了解决这些问题,Micr…...
监控异地组网怎么组网?
监控异地组网是指在不同地域的网络环境下,实现对监控设备的远程访问和管理。在传统的网络环境下,由于网络限制和设备配置等问题,监控设备的远程访问往往受到一定的限制和困扰。为了解决这个问题,引入了天联组网技术,实…...
将本地托管模型与 Elastic AI Assistant 结合使用的好处
作者:来自 Elastic James Spiteri, Dhrumil Patel 当今公共部门组织利用生成式人工智能解决安全挑战的一种方式。 凭借其筛选大量数据以发现异常模式的能力,生成式人工智能现在在帮助团队保护其组织免受网络威胁方面发挥着关键作用。 它还可以帮助安全专…...

Linux的内核态和用户态
一、Linux操作系统运行在两种不同的运行模式下:内核态(Kernel Mode)和用户态(User Mode) 内核态(Kernel Mode): 内核态也称为特权模式或系统模式,是操作系统内核执行代码…...

springboot利用Redis的Geo数据类型,获取附近店铺的坐标位置和距离列表
文章目录 GEO介绍GEO命令行应用添加地理坐标位置获取指定单位半径的全部地理位置列表springboot 的实际应用 GEO介绍 在Redis 3.2版本中,新增了一种数据类型:GEO,它主要用于存储地理位置信息,并对存储的信息进行操作。 GEO实际上…...

Vitis HLS 学习笔记--理解串流Stream(2)
目录 1. 简介 2. 极简的对比 3. 硬件模块的多次触发 4. 进一步探讨 do-while 5. 总结 1. 简介 在这篇博文中《Vitis HLS 学习笔记--AXI_STREAM_TO_MASTER-CSDN博客》,我分享了关于 AXI Stream 接口的实际应用案例。然而,尽管文章中提供了代码示例&…...

Golang | Leetcode Golang题解之第80题删除有序数组中的重复项II
题目: 题解: func removeDuplicates(nums []int) int {n : len(nums)if n < 2 {return n}slow, fast : 2, 2for fast < n {if nums[slow-2] ! nums[fast] {nums[slow] nums[fast]slow}fast}return slow }...

uniapp自定义websocket类实现socket通信、心跳检测、连接检测、重连机制
uniapp自定义websocket类实现socket通信、心跳检测、检测连接、重连机制,仿vue-socket插件功能实现发送序列号进行连接检测,发送消息时42【key,value】格式,根据后端返回数据和需要接收到的数据做nsend与onSocketMessage的修改 //使用socket…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

QMC5883L的驱动
简介 本篇文章的代码已经上传到了github上面,开源代码 作为一个电子罗盘模块,我们可以通过I2C从中获取偏航角yaw,相对于六轴陀螺仪的yaw,qmc5883l几乎不会零飘并且成本较低。 参考资料 QMC5883L磁场传感器驱动 QMC5883L磁力计…...

网站指纹识别
网站指纹识别 网站的最基本组成:服务器(操作系统)、中间件(web容器)、脚本语言、数据厍 为什么要了解这些?举个例子:发现了一个文件读取漏洞,我们需要读/etc/passwd,如…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...
 error)
【前端异常】JavaScript错误处理:分析 Uncaught (in promise) error
在前端开发中,JavaScript 异常是不可避免的。随着现代前端应用越来越多地使用异步操作(如 Promise、async/await 等),开发者常常会遇到 Uncaught (in promise) error 错误。这个错误是由于未正确处理 Promise 的拒绝(r…...
)
华为OD最新机试真题-数组组成的最小数字-OD统一考试(B卷)
题目描述 给定一个整型数组,请从该数组中选择3个元素 组成最小数字并输出 (如果数组长度小于3,则选择数组中所有元素来组成最小数字)。 输入描述 行用半角逗号分割的字符串记录的整型数组,0<数组长度<= 100,0<整数的取值范围<= 10000。 输出描述 由3个元素组成…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
