少的缓存穿透是缓存击穿,大量的是缓存雪崩
相关文章:

少的缓存穿透是缓存击穿,大量的是缓存雪崩
只要请求穿过了缓存层,直接打到了数据库,我就把这个现象理解为缓存穿透。 只要缓存失效了,就会出现缓存穿透,然后根据失效缓存数量的多少,划分出缓存击穿和缓存雪崩 缓存一致性 先改redis再改mysql。...

设备能耗数据在线监测
在追求可持续发展和绿色经济的当下,企业对于设备能耗的管理愈发重视。设备能耗数据在线监测,不仅能帮助企业实时掌握设备的运行状况,还能为企业节能减排、降低运营成本提供有力支持。HiWoo Cloud平台凭借其先进的技术和丰富的经验,…...

springboot整合websocket,超简单入门
springBoot整合webSocket,超简单入门 webSocket简洁 WebSocket 是一种基于 TCP 协议的全双工通信协议,它允许客户端和服务器之间建立持久的、双向的通信连接。相比传统的 HTTP 请求 - 响应模式,WebSocket 提供了实时、低延迟的数据传输能力。…...

代码随想录算法训练营第三十四天| 860.柠檬水找零 406.根据身高重建队列 452. 用最少数量的箭引爆气球
860.柠檬水找零 题目链接 思路 三种情况,一种贪心,在bill为20时,有一次贪心选择:优先考虑先找105,再考虑找3*5,因为5可以用于bill10和bill20两种情况 解题方法 第一种:bill5,直接收 第二种…...
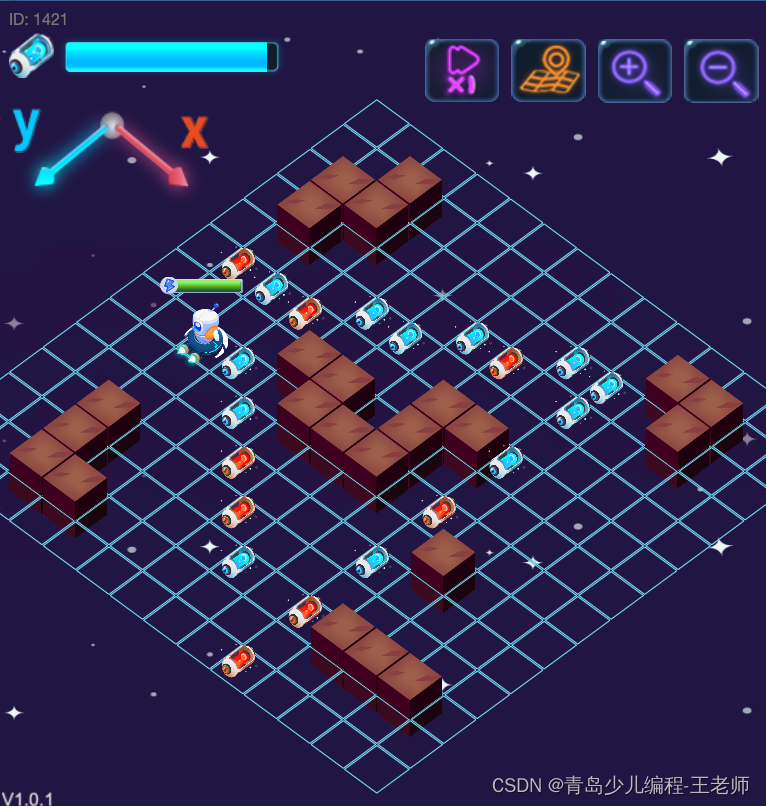
ICode国际青少年编程竞赛- Python-2级训练场-识别循环规律2
ICode国际青少年编程竞赛- Python-2级训练场-识别循环规律2 1、 for i in range(3):Dev.step(3)Dev.turnRight()Dev.step(4)Dev.turnLeft()2、 for i in range(3):Spaceship.step(3)Spaceship.turnRight()Spaceship.step(1)3、 Dev.turnLeft() Dev.step(Dev.x - Item[1].…...

12.轻量级锁原理及其实战
文章目录 轻量级锁原理及其实战1.轻量级锁的核心原理2.轻量级锁的演示2.1.轻量级锁的演示代码2.2.结果分析 3.轻量级锁的分类3.1.普通自旋锁3.2.自适应自旋锁 4.轻量级锁的膨胀 轻量级锁原理及其实战 引入轻量级锁的主要目的是在多线程环境竞争不激烈的情况下, 通过…...
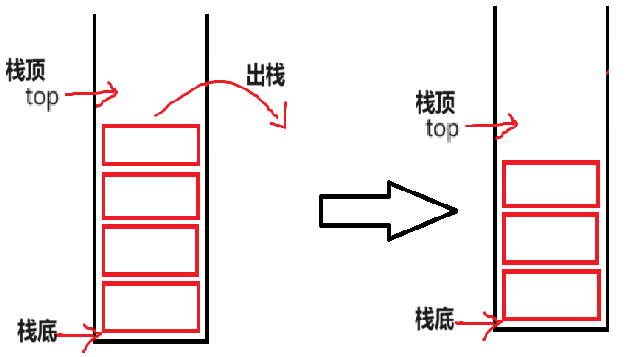
栈结构(c语言)
1.栈的概念 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 压栈&am…...

【C++】C/C++中新const用法:const成员
欢迎来到CILMY23的博客 本篇主题为: C/C中新const用法:const成员 个人主页:CILMY23-CSDN博客 系列专栏:Python | C | C语言 | 数据结构与算法 | 贪心算法 | Linux 感谢观看,支持的可以给个一键三连,点赞…...

武汉凯迪正大—钢管焊缝裂纹探伤仪
产品概述 武汉凯迪正大无损探伤仪是一种便携式工业无损探伤仪器, 能够快速便捷、无损伤、精确地进行工件内部多种缺陷(裂纹、夹杂、气孔等)的检测、定位、评估和诊断。既可以用于实验室,也可以用于工程现场。 设置简单,…...

为什么 IP 地址通常以 192.168 开头?
在网络配置中,我们经常会遇到以 192.168 开头的 IP 地址,例如 192.168.0.1 或者 192.168.1.100。 这些地址通常用于局域网中,但为什么要选择以 192.168 开头呢? 本文将深入探讨这个问题,并解释其背后的原因和历史渊源…...

elementUi中的el-table合计行添加点击事件
elementUi 文档中,合计行并没有点击事件,这里自己实现了合计行的点击事件。 created() {this.propertyList [{ property: order, label: 序号 },{ property: deptName, label: 单位名称 },{ property: contentPublishQuantity, label: 文章数量 },{ pro…...

Zookeeper集群搭建的一些问题
问题描述一: Cannot open channel to 2 at election address /192.168.60.132:3888解决方案: 查看zookeeper配置文件zoo.cfg / zoo_sample.cfg中集群配置部分 server.1zoo1-net1:2888:3888|zoo1-net2:2889:3889 server.2zoo2-net1:2888:3888|zoo2-net2…...
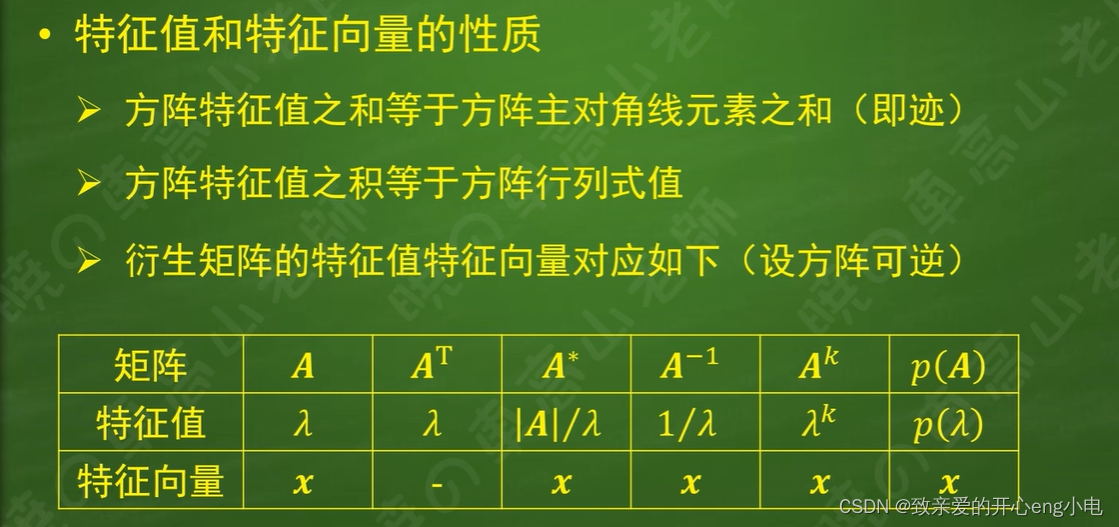
【线性代数】俗说矩阵听课笔记
基础解系的概念 线性方程组的解 21行列式和矩阵秩Rank的等价刻画 子式 标准型 利用子式求解矩阵的rank 24零积秩不等式 齐次线性方程组的基础解系 rank的两个重要结论 ¥25伴随矩阵的rank 奇异矩阵:行列式0的矩阵 31线性相关,线性无关&#…...

物联网技术在数字化工厂中的应用,你知道多少?——青创智通
工业物联网解决方案-工业IOT-青创智通 物联网(IoT)技术在数字化工厂的应用正日益成为工业革命的重要推动力。随着科技的飞速发展,物联网技术不断革新,其在数字化工厂中的应用也呈现出愈发广泛和深入的态势。本文将详细探讨物联网…...
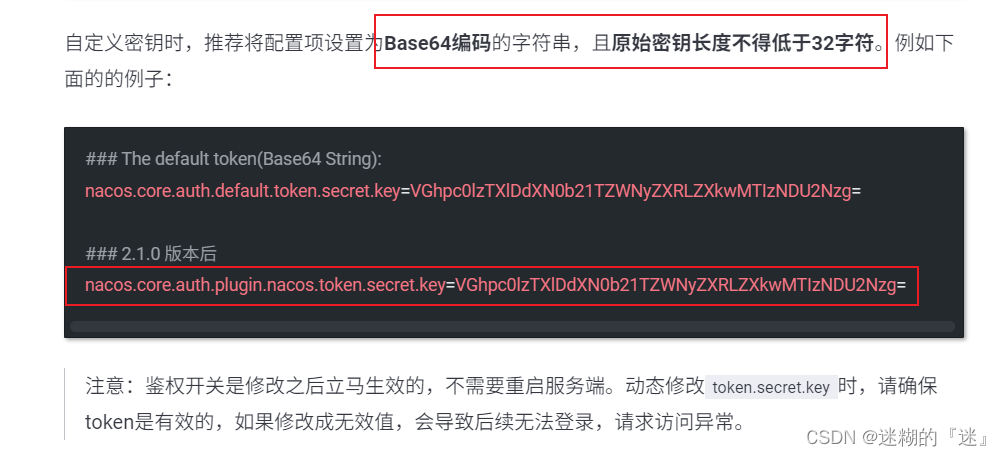
nacos开启登录开关启动报错“Unable to start embedded Tomcat”
nacos 版本:2.3.2 2.2.2版本之前的Nacos默认控制台,无论服务端是否开启鉴权,都会存在一个登录页;在之后的版本关闭了默认登录页面,无需登录直接进入控制台操作。在这里我们可以在官网可以看到相关介绍 而我现在所用的…...
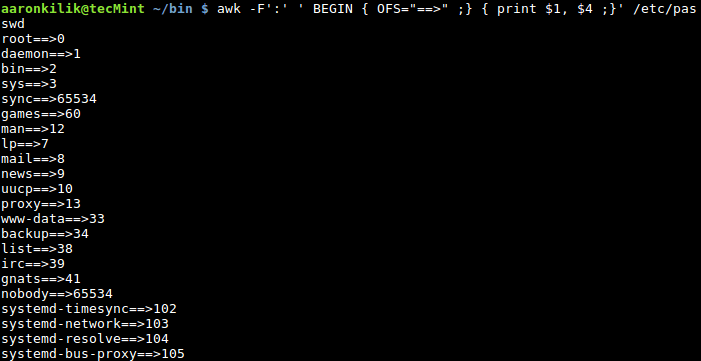
Linux|了解如何使用 awk 内置变量
引言 当我们揭开 Awk 功能部分时,我们将介绍 Awk 中内置变量的概念。您可以在 Awk 中使用两种类型的变量:用户定义的变量和内置变量。 内置变量的值已经在 Awk 中定义,但我们也可以仔细更改这些值,内置变量包括: FILEN…...

代码随想录-算法训练营day29【回溯算法05:递增子序列、全排列】
代码随想录-035期-算法训练营【博客笔记汇总表】-CSDN博客 第七章 回溯算法part05* 491.递增子序列 * 46.全排列 * 47.全排列 II详细布置 491.递增子序列 本题和大家刚做过的 90.子集II 非常像,但又很不一样,很容易掉坑里。 https://programmercarl.com…...

704. 二分查找
Problem: 704. 二分查找 🐷我的leetcode主页 文章目录 题目分类思路什么是二分查找如何理解时间复杂度 解题方法Code 题目 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target&a…...

php回车变br、php显示br
在 PHP 中,如果你想将回车符(\n)转换为 HTML 的 <br> 标签来实现换行显示,可以使用内置函数 nl2br()。这个函数会将文本中的换行符替换为 <br> 标签。以下是使用 nl2br() 函数的示例代码: <?php $tex…...
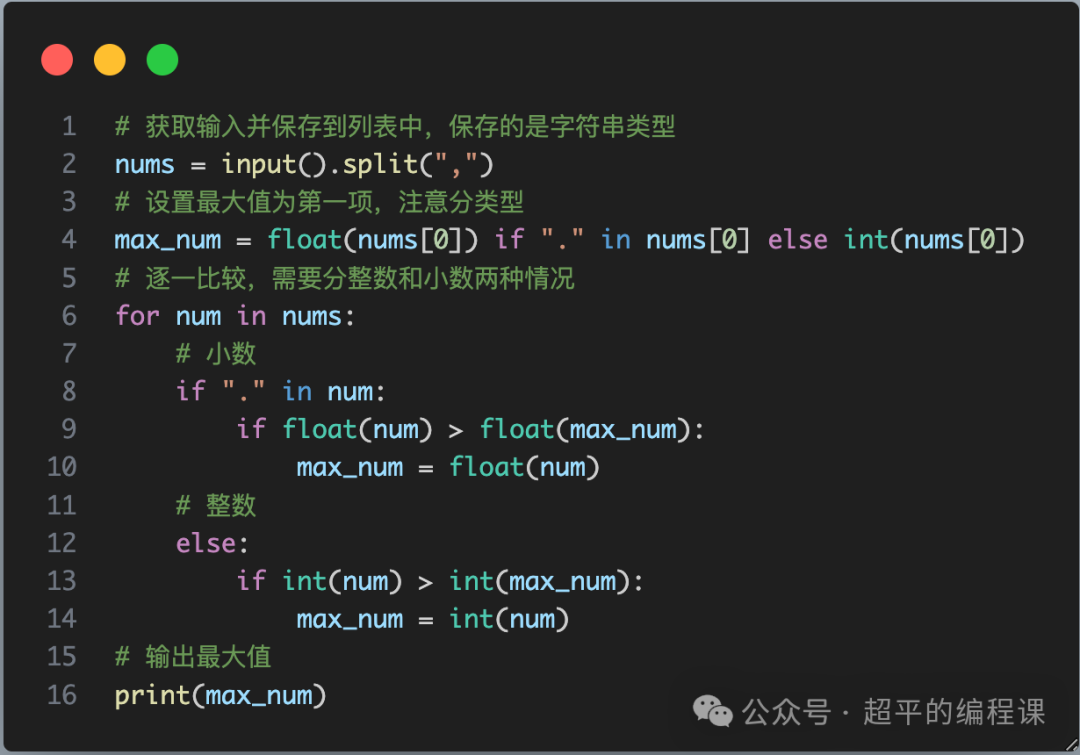
找最大数字-第12届蓝桥杯国赛Python真题解析
[导读]:超平老师的Scratch蓝桥杯真题解读系列在推出之后,受到了广大老师和家长的好评,非常感谢各位的认可和厚爱。作为回馈,超平老师计划推出《Python蓝桥杯真题解析100讲》,这是解读系列的第60讲。 找最大数字&#…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣(LeetCode) 思路 使用两个栈:一个存储重复次数,一个存储字符串 遍历输入字符串: 数字处理:遇到数字时,累积计算重复次数左括号处理:保存当前状态&a…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...
