贪心算法-活动选择问题背包问题
目录
活动选择问题
无重叠区间-Leetcode 435
分数背包问题--贪心解法
贪心法
0-1 背包问题
贪心法
贪心算法的局限
Set cover problem
活动选择问题
分析:
/* 要在一个会议室举办n个活动 - 每个活动有它们各自的起始和结束时间 - 找出在时间上互不冲突的活动组合,能够最充分利用会议室(举办的活动次数最多)例10 1 2 3 4 5 6 7 8 9|--------) |--------)|--------)选1 3 能够举办2个活动例20 1 2 3 4 5 6 7 8 9|---)|---)|-----------------------)|-------)|---)|---------------)4个活动几种贪心策略1.优先选择持续时间最短的活动 以下情形不满足方案out0 1 2 3 4 5 6 7 8 9|---------------)|-------)|----------------)\2.优先选择冲突最少的活动编号 0 1 2 3 4 5 6 7 8 91 |-------) 3 选中2 |-------) 43 |-------) 44 |-------) 45 |-------) 46 |-------) 2 选中7 |------------) 48 |--------) 49 |--------) 410 |--------) 411 |-------) 3 选中但实际上应该是1 5 7 11 所以这个也不行3. 优先选择最先开始的活动 不行0 1 2 3 4 5 6 7 8 9|-----------------------------------)|---)|---)|---)4. 优先选择最先结束的活动*/
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Comparator;
import java.util.List;/*** <h1>活动选择问题 - 贪心解法</h1>* Leetcode 435 无重叠区间本质就是活动选择问题*/
public class ActivitySelectionProblem {static class Activity{int index;int start;int finish;public Activity(int index,int start,int finish){this.index = index;this.start = start;this.finish = finish;}public int getFinish(){return finish;}@Overridepublic String toString(){return "Activity("+index+")";}}public static void main(String[] args) {Activity[] activities = new Activity[]{new Activity(0, 1, 3),new Activity(1, 2, 4),new Activity(2, 3, 5)};
// Activity[] activities = new Activity[]{
// new Activity(0, 1, 2),
// new Activity(1, 3, 4),
// new Activity(2, 0, 6),
// new Activity(3, 5, 7),
// new Activity(4, 8, 9),
// new Activity(5, 5, 9)
// };Arrays.sort(activities, Comparator.comparingInt(Activity::getFinish));System.out.println(Arrays.toString(activities));select(activities, activities.length);}public static void select(Activity[] activities, int length) {List<Activity>result = new ArrayList<>();Activity prev = activities[0];result.add(prev);for(int i = 1;i<length;i++){Activity curr = activities[i]; //当前正在处理的活动if (curr.start >= prev.finish) {result.add(curr);prev = curr;}}for (Activity activity : result) {System.out.println(activity);}}
}
435. 无重叠区间 - 力扣(LeetCode)
无重叠区间-Leetcode 435
| 题目编号 | 题目标题 | 算法思路 |
|---|---|---|
| 435 | 无重叠区间 | 贪心 |
class Solution {public int eraseOverlapIntervals(int[][] intervals) {if(intervals.length==0){return 0;}Arrays.sort(intervals,Comparator.comparingInt(a->a[1]));int i,j;i=0;int count =1;for(j = 1;j<intervals.length;j++){if(intervals[j][0] >= intervals[i][1]){i = j;count++;}}return intervals.length-count;}
}-
找到不重叠的最多的活动数(count),即活动选择问题原始需求
-
在此基础上,活动总数 - count,就是题目要的排除数量
分数背包问题--贪心解法
贪心法
/* 1. n个物品都是液体,有重量和价值 2. 现在你要取走 10升 的液体 3. 每次可以不拿,全拿,或拿一部分,问最高价值是多少编号 重量(升) 价值0 4 24 水1 8 160 牛奶 选中 7/82 2 4000 五粮液 选中3 6 108 可乐4 1 4000 茅台 选中8140简化起见,给出的数据都是【价值/重量】能够整除,避免计算结果中出现小数,增加心算难度*/
import java.util.Arrays;
import java.util.Comparator;public class FractionalKnapsackProblem {static class Item {int index;int weight;int value;public Item(int index, int weight, int value) {this.index = index;this.weight = weight;this.value = value;}public int unitPrice() {return value / weight;}@Overridepublic String toString() {return "Item(" + index + ")";}}public static void main(String[] args) {Item[] items = new Item[]{new Item(0, 4, 24),new Item(1, 8, 160),new Item(2, 2, 4000),new Item(3, 6, 108),new Item(4, 1, 4000),};select(items, 10);}static void select(Item[] items, int total) {Arrays.sort(items, Comparator.comparingInt(Item::unitPrice).reversed());//reversed()降序int remainder = total;int max = 0;for (Item item : items) {if (remainder - item.weight >= 0) {//一次能够拿完max += item.value;remainder -= item.weight;} else {//拿不完max += remainder * item.unitPrice();break;}}System.out.println("最高价值为:" + max);}}0-1 背包问题
贪心法
可能得不到最优解
/*0-1 背包问题1. n个物品都是固体,有重量和价值2. 现在你要取走不超过 10克 的物品3. 每次可以不拿或全拿,问最高价值是多少编号 重量(g) 价值(元)0 1 1_000_000 钻戒一枚 选中1 4 1600 黄金一块 4002 8 2400 红宝石戒指一枚 3003 5 30 白银一块按照分数背包问题解法: 1001630 但其实不对 应该是1002400*/
import java.util.Arrays;
import java.util.Comparator;public class KnapsackProblem {static class Item {int index;int weight;int value;public Item(int index, int weight, int value) {this.index = index;this.weight = weight;this.value = value;}public int unitValue() {return value / weight;}@Overridepublic String toString() {return "Item(" + index + ")";}}public static void main(String[] args) {Item[] items = new Item[]{new Item(0, 1, 1_000_000),new Item(1, 4, 1600),new Item(2, 8, 2400),new Item(3, 5, 30)};select(items, 10);}static void select(Item[] items, int total) {Arrays.sort(items, Comparator.comparingInt(Item::unitValue).reversed());int max = 0; // 最大价值for (Item item : items) {System.out.println(item);if (total >= item.weight) { // 可以拿完total -= item.weight;max += item.value;} else { // 拿不完
// max += total * item.unitValue();
// break;}}System.out.println("最大价值是:" + max);}
}贪心算法的局限
| 问题名称 | 是否能用贪心得到最优解 | 替换解法 |
|---|---|---|
| Dijkstra(不存在负边) | ✔️ | |
| Dijkstra(存在负边) | ❌ | Bellman-Ford |
| Prim | ✔️ | |
| Kruskal | ✔️ | |
| 零钱兑换 | ❌ | 动态规划 |
| Huffman 树 | ✔️ | |
| 活动选择问题 | ✔️ | |
| 分数背包问题 | ✔️ | |
| 0-1 背包问题 | ❌ | 动态规划 |
Set cover problem
集合覆盖问题
这个问题后面会出文章! 敬请期待!
相关文章:

贪心算法-活动选择问题背包问题
目录 活动选择问题 无重叠区间-Leetcode 435 分数背包问题--贪心解法 贪心法 0-1 背包问题 贪心法 贪心算法的局限 Set cover problem 活动选择问题 分析: /* 要在一个会议室举办n个活动 - 每个活动有它们各自的起始和结束时间 - 找出在时间上互不冲突的活动组合,能…...

Web3工具集合 - 00
使用 React 和 Material-UI 构建的 Web3 工具集合 大家好! 我很高兴向大家介绍我最近刚启动了一个项目:Web3 工具集合。 这个项目的目的是一个集成各种 Web3 工具的网站,旨在为开发人员和加密货币爱好者提供便捷的工具和资源。 特点&#…...
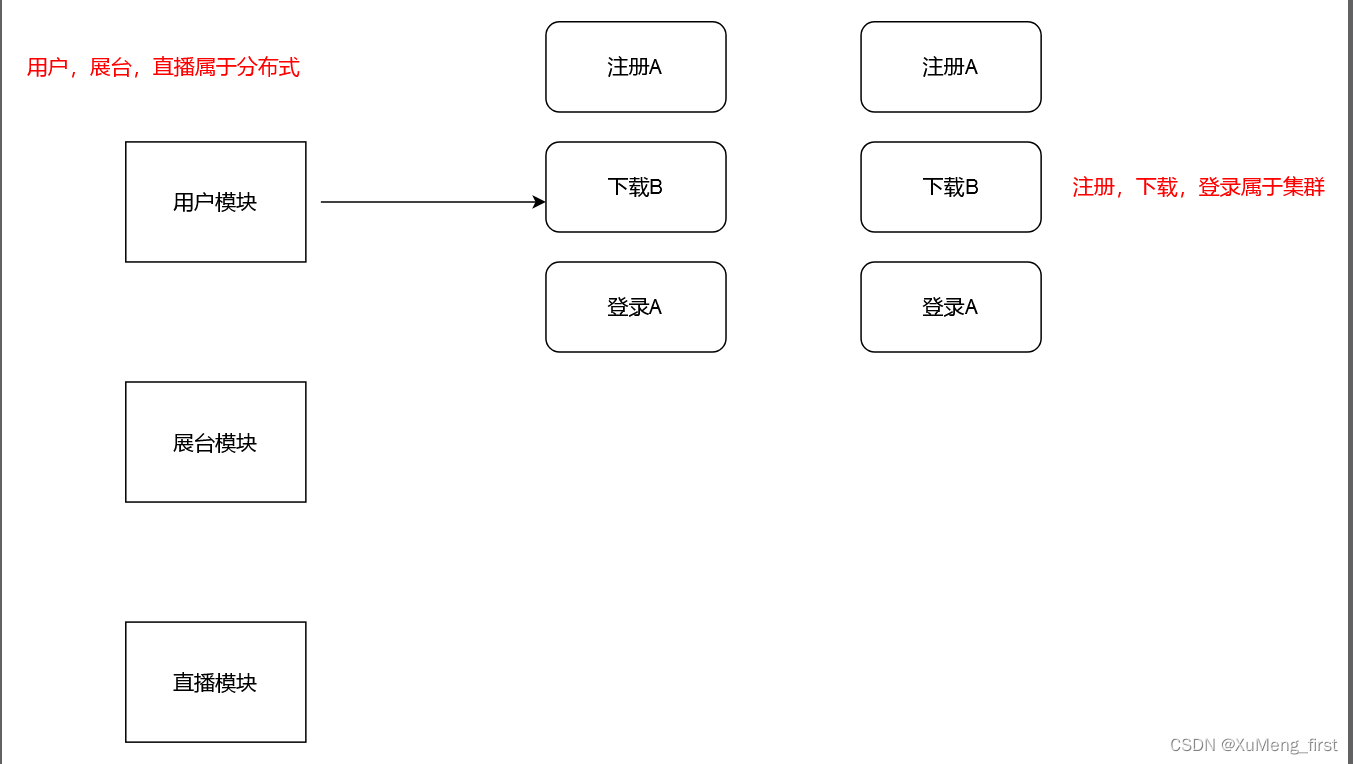
分布式与集群的区别
先说区别: 分布式是并联工作的,集群是串联工作的。 分布式中的每一个节点都可以做集群。而集群并不一定就是分布式的。 集群举例:比如新浪网,访问的人很多,他可以做一个集群,前面放一个相应的服务器&…...

学习心得:如何开始学习一款MCU
一、MCU简介 任何一款MCU,其基本原理和功能都是大同小异,所不同的只是其外围功能模块的配置及数量、指令系统等。对于指令系统,虽然形式上看似千差万别,但实际上只是符号的不同,其所代表的含义、所要完成的功能和寻址…...
顺序表的实现(迈入数据结构的大门)(1)
上一节我们认识到了什么是数据结构 这一节我们就来实现第一个数据结构的实现 思考一个问题: 假定一个数组,空间为10,已经使用了5个,向其中插入数据的步骤: 1.插入数据,我们先要求数组长度,其…...
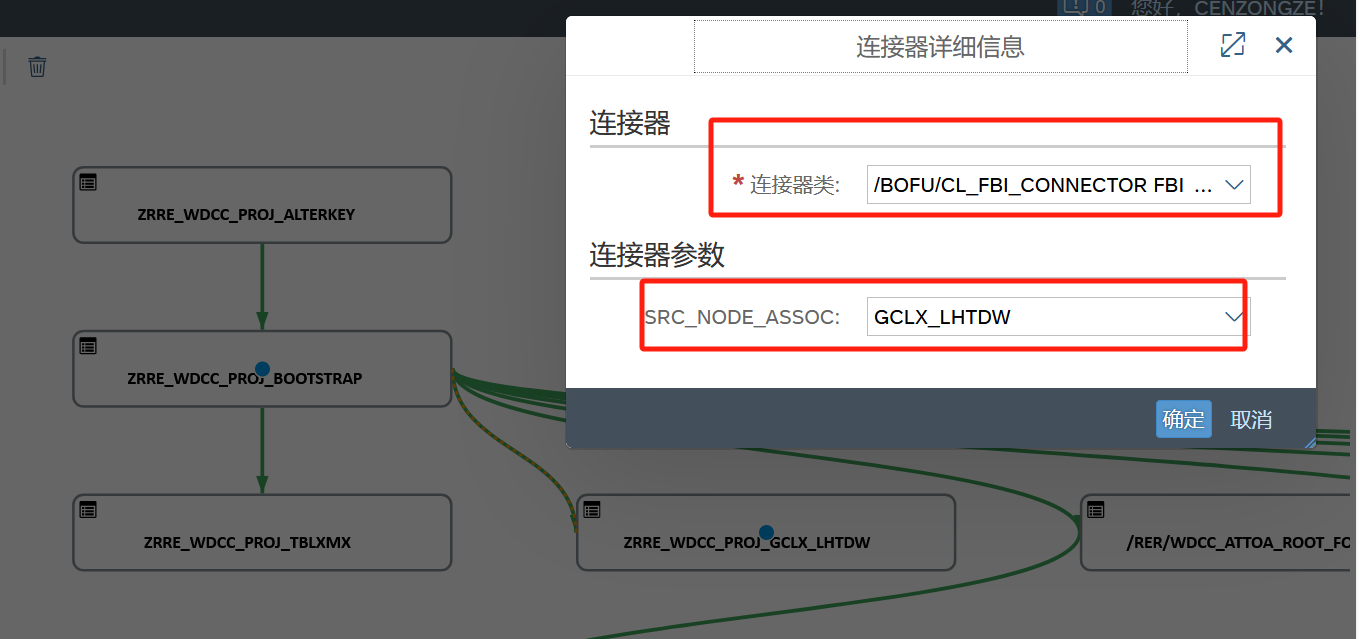
RERCS系统-WDA+BOPF框架实战例子 PART 1-新建List UIBB(列表组件)并分配Feeder Class和Node Element
需求背景: 已有的项目主数据功能,新增一个列表UIBB显示主数据额外的关联数据明细。 1、Fiori页面通过右键-技术帮助打开对应的组件配置; 2、双击对应的组件配置,调整对应的页面新建UIBB; 3、填写对应的UIBB属性字段&a…...

如何从 iPhone 恢复已删除或丢失的联系人?
不小心删除了您的 iPhone 联系人?不用担心。我们将向您展示如何从 iPhone或 iPad恢复已删除或丢失的联系人。当您从 iPhone 中删除联系人时,您可能认为无法将其恢复。但事实是,您可以从 iPhone 或 iPad 恢复已删除的联系人,因为它…...

RISCV 外部GCC 工具链安装@FreeBSD15
在交叉编译的时候,可以使用FreeBSD15默认的工具链:LLVM 也可以使用GCC工具链,GCC可以使用现成pkg包安装,也可以编译安装。 LLVM的特点是高移植性和高效,但学习成本高。GCC的特点是成熟稳定,但优化能力有限…...

全栈开发之路——前端篇(9)插槽、常用api和全局api
全栈开发一条龙——前端篇 第一篇:框架确定、ide设置与项目创建 第二篇:介绍项目文件意义、组件结构与导入以及setup的引入。 第三篇:setup语法,设置响应式数据。 第四篇:数据绑定、计算属性和watch监视 第五篇 : 组件…...

减瘦误区、雷点、陷阱和挑战怎么应对
在减瘦过程中,很多肥胖人群都容易踩到坑。比如陷入误区,认为只有短期快速的减调方式方法,才值得尝试,而忽视身体健康;或是踩到雷点,轻信强速方剂或方法,结果身体产生了排斥或根本没效用白花钱&a…...

Leetcode—946. 验证栈序列【中等】
2024每日刷题(133) Leetcode—946. 验证栈序列 实现代码 class Solution { public:bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {int left 0;for(int i 0; i < popped.size(); i) {while(left &…...

Selenium定位方法及代码
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

GitHub搭建免费博客
一、GitHub仓库准备 搭建博客需要准备两个仓库。一个存放博客图床的仓库,另一个存放博客网站的仓库。 1.1、图床创建 新建仓库 第一步: 第二步: 生成Token令牌 点击右上角头像->Settings->下拉,直到左侧到底&#…...
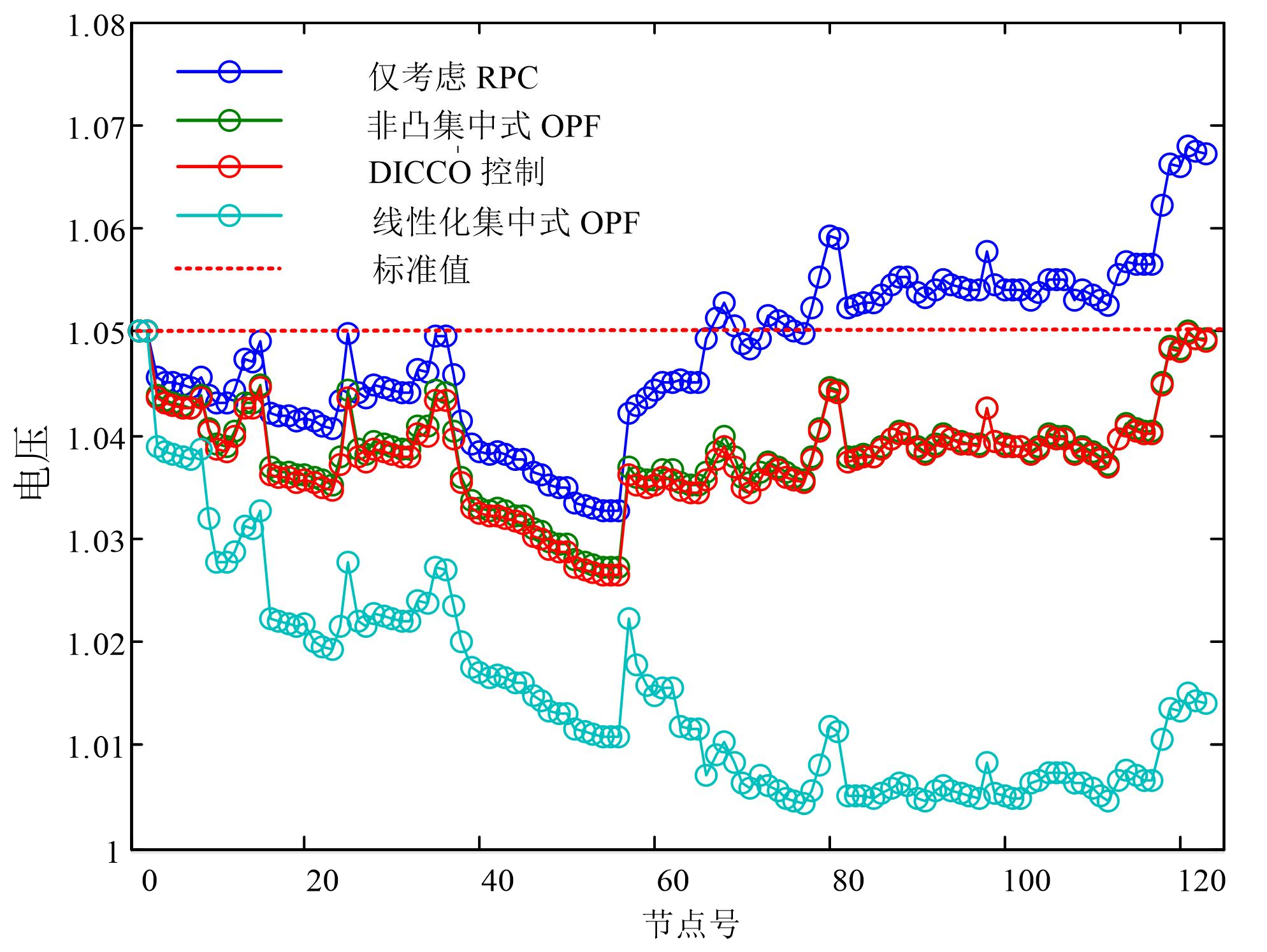
开源代码分享(28)-含分布式光伏的配电网集群划分和集群电压协调控制
参考文献: [1] Chai Y , Guo L , Wang C ,et al.Network Partition and Voltage Coordination Control for Distribution Networks With High Penetration of Distributed PV Units[J].IEEE Transactions on Power Systems, 2018:3396-3407.DOI:10.1109/TPWRS.2018…...
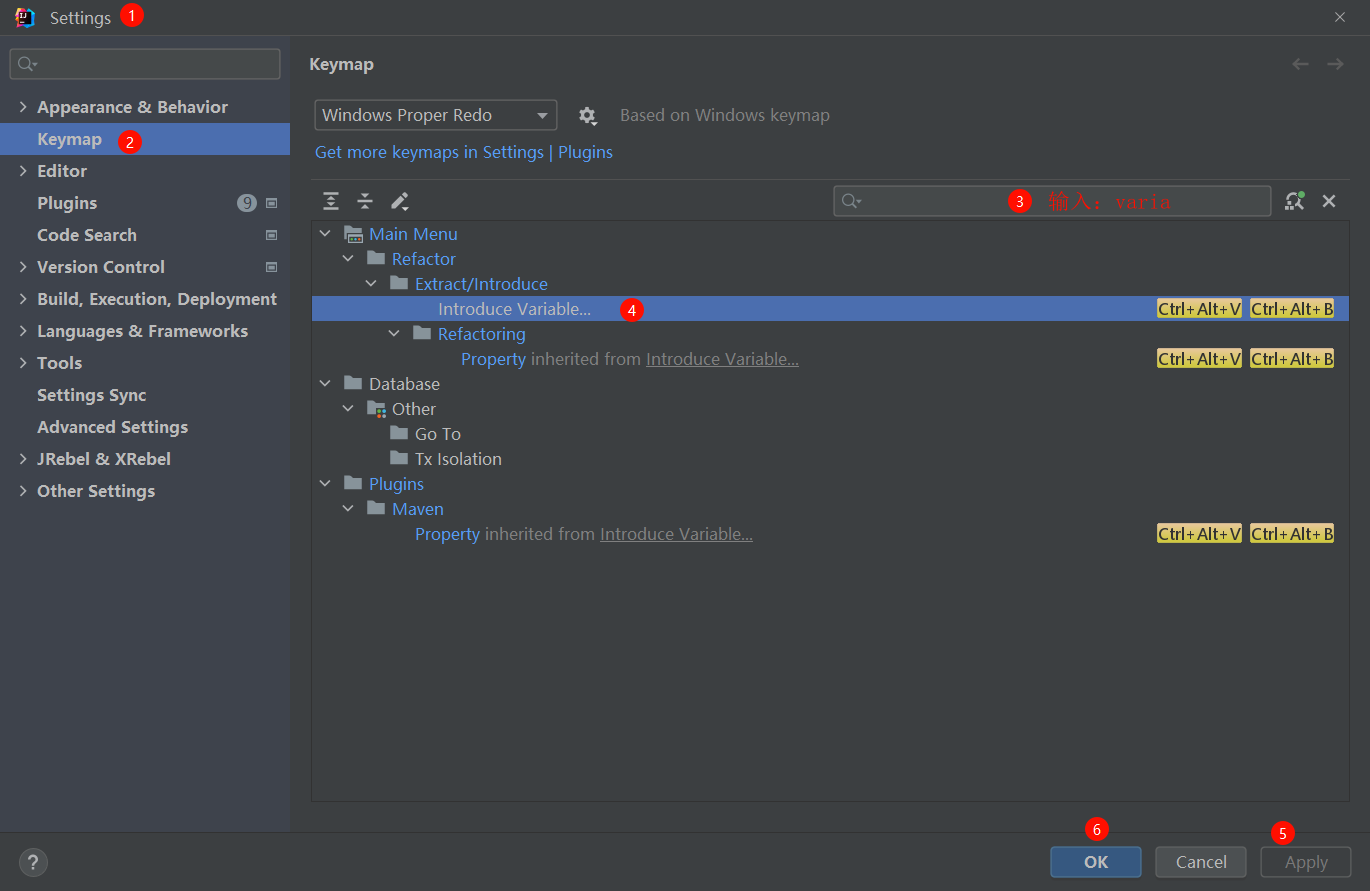
idea-自我快捷键-2
1. 书签 创建书签: 创建书签:F11创建特色标记书签:Ctrl F11快速添加助记符书签:ctrl shift 数字键 查看书签: shift F11快速定位到助记符书签:Ctrl 数字键 删除书签: delete 2. 自动…...
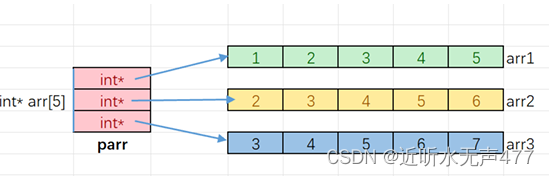
深入学习指针3
目录 前言 1.二级指针 2.指针数组 3.指针数组模拟二维数组 前言 Hello,小伙伴们我又来了,上期我们讲到了数组名的理解,指针与数组的关系等知识,那今天我们就继续深入到学习指针域数组的练联系,如果喜欢作者菌生产的内容还望不…...

礼赞劳动节,致敬劳动者。节日随想:疾笔耕耘也是一种劳动方式。
马克思也快诞辰了206年了,恩格斯领导的第二国际通过的决议节日也迎来了134岁的生日了,我也继续在劳动的路上。 五月是值得纪念的日子,作为一名无上光荣的分子,无比仰慕崇拜的两位先驱前辈大胡子,其一 生于斯࿰…...

学习Java的日子 Day45 HTML常用的标签
Day45 HTML 1.掌握常用的标签 1.1 标题标签 h1-h6 <h1>一级标签</h1> <h2>二级标签</h2> <h3>三级标签</h3> <h4>四级标签</h4> <h5>五级标签</h5> <h6>六级标签</h6> 显示特点: * 文字…...

兔子与狮子
兔子与狮子 一只骨瘦如柴的兔子,在慢悠悠地吃草 趴在边上的狮子说,多吃点吧,你身上一点肉都没有 兔子说,我正在减肥,体重越来越轻,骨头越来越硬 狮子舔了舔嘴巴,你再狡猾,也是我的…...

GNU/Linux - 系统启动流程及rcS脚本介绍
Linux系统启动流程 在 Linux 系统启动过程中,会按特定顺序执行多个脚本和初始化例程,以使系统进入可用状态。虽然具体顺序可能因 Linux 发行版和版本而异,但以下是典型执行顺序的概括性概述: 1. BIOS/UEFI: 系统开机后…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

【磁盘】每天掌握一个Linux命令 - iostat
目录 【磁盘】每天掌握一个Linux命令 - iostat工具概述安装方式核心功能基础用法进阶操作实战案例面试题场景生产场景 注意事项 【磁盘】每天掌握一个Linux命令 - iostat 工具概述 iostat(I/O Statistics)是Linux系统下用于监视系统输入输出设备和CPU使…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

站群服务器的应用场景都有哪些?
站群服务器主要是为了多个网站的托管和管理所设计的,可以通过集中管理和高效资源的分配,来支持多个独立的网站同时运行,让每一个网站都可以分配到独立的IP地址,避免出现IP关联的风险,用户还可以通过控制面板进行管理功…...
