基础算法,贪心算法,贪心策略,OJ练习
文章目录
- 一、概念
- 二、OJ练习
- 2.1 区间选点
- 2.2 区间合并
- 2.3 区间
- 2.4 合并果子
- 2.5 排队接水
- 2.6 货仓选址
- 2.7 防晒
- 2.8 畜栏预定
- 2.9 雷达设备
- 2.10 国王游戏
- 2.11 耍杂技的牛
- 2.12 给树染色
- 2.13 任务
- 2.14 能量石
- 三、总结
一、概念
贪心是一种在每次决策时采取当前意义下最优策略的算法,因此,使用贪心法要求问题的整体最优性可以由局部最优性导出。贪心算法的正确性需要证明,常见的证明手段有:
- 微扰(邻项交换)
- 证明在任意局面下,任何对局部最优策略的微小改变都会造成整体结果变差。经常用于以“排序”为贪心策略的证明。
- 范围缩放
- 证明任何对局部最优策略作用范围的扩展都不会造成整体结果变差
- 决策包容性
- 证明在任意局面下,作出局部最优决策以后,在问题状态空间中的可达集合包含了作出其他任何决策后的可达集合。换言之,这个局部最优策略提供的可能性包含其他所有策略提供的可能性。
- 反证法
- 数学归纳法
贪心算法在算法体系中较为特殊,这里通过几道例题来体会贪心算法的应用。
二、OJ练习
2.1 区间选点
区间选点 - 45D - Codeforces
题目保证了有解,我们该如何选出可行解呢?
我们考虑把区间按照右端点升序排序,然后遍历所有区间,对于每个区间选取区间内没有被选取的最左端点
如何证明正确性?——反证法
假设按照上述策略出现某个区间无点可选,该区间为[l, r],说明有r - l + 1个右端点不小于l,不超过r的区间选择了[l, r]内的r - l + 1个点
它们选择[l, r]内的点说明它们在[0, l - 1]的部分都被选完了,否则按照靠左原则应该选取[0, l - 1]的点,那么[l, r]内就存在r - l + 2个区间的右端点,此时原问题无解,与题目条件矛盾,故策略正确。
对于区间问题通用操作是按照某端点排序,在处理区间问题没有头绪的时候可以试着排序来寻找突破口。
n = int(input())lines = []for _ in range(n):a, b = map(int, input().split())lines.append((a, b, _))
lines.sort(key=lambda x: x[1])st = set()
ans = [0] * n
for l, r, idx in lines:for i in range(l, r + 1):if not (i in st):st.add(i)ans[idx] = ibreakfor x in ans:print(x, end=' ')2.2 区间合并
P2082 区间覆盖(加强版) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
即求区间合并后的长度
那么我们将区间按照左端点升序排序,然后顺序遍历区间
记录当前合并区间的左端点L,右端点R,对于遍历到的区间[l, r]
如果l > R,那么说明和前面的区间不相交,我们累加前面区间的长度后更新当前合并区间为[l, r]
否则,更新R = max(R, r)
证明很简单,就是假设存在两个可以合并的区间没有合并,然后反证推出矛盾即可,不再赘述。
n = int(input())
lines = [tuple(map(int, input().split())) for _ in range(n)]
lines.sort(key=lambda x: x[0])res = 0
L, R = 0, -1
for x, y in lines:if x <= R:R = max(R, y)else:res += R - L + 1L, R = x, y
print(res + (R - L + 1))
2.3 区间
[P2434 SDOI2005] 区间 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
和上一道题做法一样,是在上一道题目的基础上加上了输出具体方案
我们只需开一个数组表示当前的不合并区间数组,如果当前区间和最后一个不相交就加入数组,否则就维护最后一个区间的最右端点
n = int(input())
lines = [tuple(map(int, input().split())) for _ in range(n)]
lines.sort(key=lambda x: x[0])res = 0
ans = [lines[0]]
for x, y in lines:if x <= ans[-1][1]:ans[-1] = (ans[-1][0], max(ans[-1][1], y))else:ans.append((x, y))
for x, y in ans:print(x, y)
2.4 合并果子
148. 合并果子 - AcWing题库
很明显的贪心思路,每次区所有堆中最小的两堆合并即可
为什么是正确的呢?
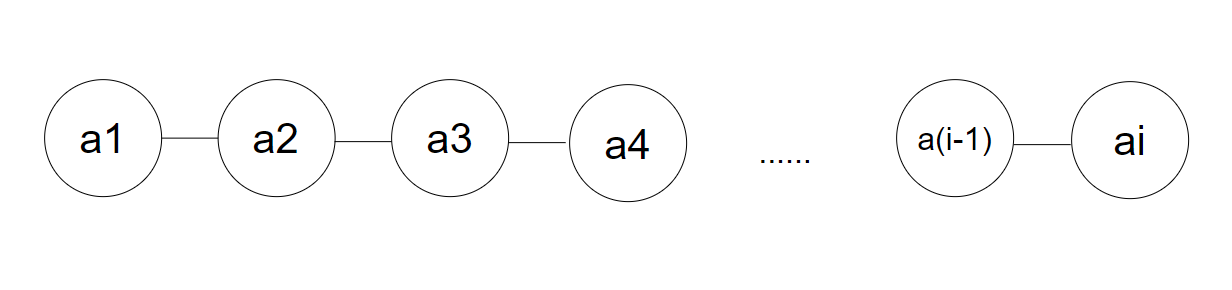
我们合并的过程其实可以构造出一棵树,这棵树和Huffman树其实是等价的。
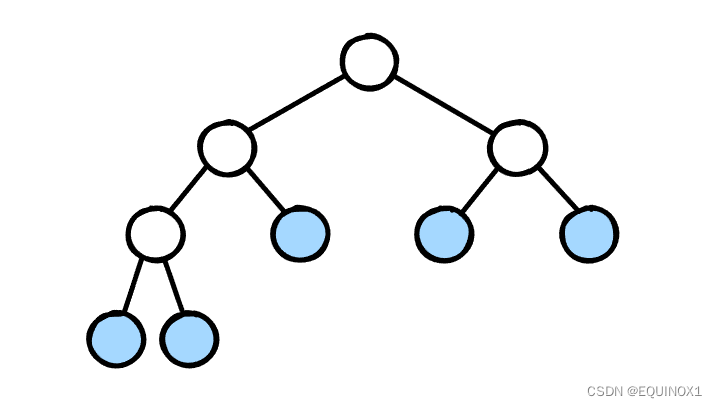
上图中蓝色代表初始的果子堆,每个结点都是由两个孩子合并而来
初始蓝色结点的贡献为深度 乘 结点权值
我们只需证明按照贪心策略得到的树中:蓝色结点的权值 * 深度之和最小即可
引理:权值最小的两个点的深度一定最深,且互为兄弟
证明:如果不是,两个点中至少有一个可以和最后一层的某个权值不小于自身的结点交换,那么两个结点可以交换到最后一层并且成为兄弟,那么 蓝色结点的权值 * 深度之和至少不会变大,甚至变小,故得证
那么最优解的值等价于 权值最小的两个点的值相加 加上 两个点合并后与剩余的n - 2个点构造出的最优树的值
同样的,我们如此迭代下去,可以构造出一棵最优解树,故得证。
import heapq
n = int(input())
a = list(map(int, input().split()))
heapq.heapify(a)
res = 0
while len(a) > 1:x = heapq.heappop(a)y = heapq.heappop(a)res += x + yheapq.heappush(a, x + y)
print(res)
2.5 排队接水
P1223 排队接水 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
每个人接的越早,它的时间就会越多人忍受
所以我们让接的少的人优先接水即可
证明也很简单,同样反证,然后总可以按照贪心策略构造出不比最优解差甚至更优的解
n = int(input())
a = [(int(x), _ + 1) for _, x in enumerate(input().split())]
a.sort()
s = 0
for i, (x, idx) in enumerate(a):s += x * (n - i - 1)print(idx, end=' ')
print('')
print('%.2f' % (s / n))
2.6 货仓选址
104. 货仓选址 - AcWing题库
很经典的中位数问题,就是数轴上找到一个点y使得,Σ|x - y|最小
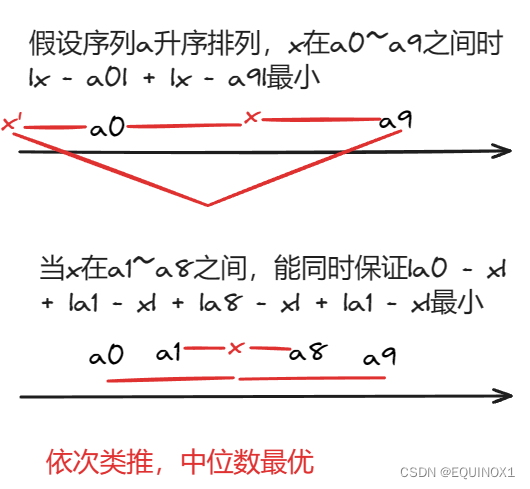
上图其实已经很明白了,当y选在两个数里面的差绝对值和总小于等于在两个数外面的差绝对值
那么我们剥洋葱似的一层一层往里钻,就会落到中位数处
n = int(input())
a = list(map(int, input().split()))
a.sort()mid = a[len(a) // 2]print(sum(abs(x - mid) for x in a))
2.7 防晒
110. 防晒 - AcWing题库
又是区间问题,不过这道题按照左右端点哪个排都能做,其实有点让每个资源发挥其最大作用的意思
怎么思考呢?我们把牛牛的区间按照右端点排序,然后顺序遍历牛牛每次选取在自己区间内最小的那个防晒霜
如何证明我们这样得到的一定是最优解?
我们可以证明对任意最优解按照贪心策略调整不会使得解变差从而得到一个最优解,我们也可以用范围缩放来证明,即我们的局部最优贪心策略对整体影响最小。
我们已经按照右端点排序,那么对于当前枚举奶牛的可用防晒霜x,y,SPF[x] < SPF[y]只有如下三种情况:
- 后面奶牛x,y都能用
- 后面奶牛只能用y
- 后面奶牛x,y都不能用
我们发现我们选择x对后面奶牛影响最小,所以贪心策略正确。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <map>
using namespace std;
#define x first
#define y second
typedef pair<int, int> PII;
const int N = 2510;int n, m;
PII w[N];
map<int, int> mp;int main(){cin >> n >> m;for(int i = 0; i < n; i ++) cin >> w[i].x >> w[i].y;for(int i = 0, a, b; i < m; i ++) cin >> a >> b, mp[a] += b;sort(w, w + n, [](const PII& a, const PII& b){return a.y < b.y;});int res = 0;for(int i = 0; i < n; i ++){ //cout << w[i].x << ' ' << w[i].y << endl;auto it = mp.lower_bound(w[i].x);if (it != mp.end() && it -> first <= w[i].y) {it -> second --, res ++;if(! it -> second) mp.erase(it);}}cout << res;return 0;
}2.8 畜栏预定
111. 畜栏预定 - AcWing题库
我们将牛按开始时间升序排序,然后枚举牛
如果对于当前牛有可以安排的畜栏(畜栏内最后一头牛结束时间不晚于当前牛的开始时间),那么我们就安排进去
如果没有,就新开一个畜栏
上述做法的正确性:
反证法:我们存在不同于上述策略的方案为更优解,只需m个畜栏,那么我们上述策略建立第m + 1个畜栏时,必然有m个畜栏的结束时间都大于当前牛的开始时间,而由于我们按照开始时间升序,故m个畜栏的最后一头牛都和当前牛区间有交集,等价于m + 1头牛两两有交集,所以我们至少需要m + 1个畜栏,矛盾,故得证。
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
using namespace std;
#define x first
#define y second
const int N = 5e4 + 10;
typedef pair<int, int> PII;
typedef pair<PII, int> PIII;
PIII lines[N];
int n, id[N];
priority_queue<PII, vector<PII>, greater<PII>> pq;
int main(){cin >> n;for(int i = 0, a, b; i < n; i ++) cin >> a >> b, lines[i] = { {a, b}, i };sort(lines, lines + n);for(int i = 0; i < n; i ++){if(pq.empty() || pq.top().x >= lines[i].x.x)pq.emplace(lines[i].x.y, id[lines[i].y] = pq.size() + 1);else{PII t = pq.top();pq.pop();t.x = lines[i].x.y;pq.emplace(t);id[lines[i].y] = t.y;}}cout << pq.size() << endl;for(int i = 0; i < n; i ++) cout << id[i] << endl;return 0;
}
2.9 雷达设备
112. 雷达设备 - AcWing题库
对于每个小岛而言,可以覆盖它的点对应x轴上一个区间,那么每个小岛就能够有一个可监测区间
我们只需选择尽可能少的点使得每个区间都被覆盖到即可,这就转化为了区间选点问题
我们将区间按照右端点排序,然后如果当前区间左端点小于覆盖区间的右端点,说明该区间可以被前面覆盖区间的点
否则我们就开一个新区间,所选的点为当前区间的右端点
from math import sqrt
n, d = map(int, input().split())
eps = 1e-6
lines = []
for _ in range(n):x, y = map(int, input().split())if y - d > eps:print(-1)exit(0)dx = sqrt(d * d - y * y)lines.append((x - dx, x + dx))lines.sort(key=lambda x: x[1])
ed = -2000
res = 0
for l, r in lines:if l - ed > eps:res += 1ed = r
print(res)
2.10 国王游戏
114. 国王游戏 - AcWing题库
本题贪心策略为:将大臣按照左手乘右手升序排序,此时的最大值最小
证明策略:临项交换(微扰)
我们假设最优解不是按照上述策略得到,那么一定存在a[i] * b[i] >= a[i + 1] * b[i + 1]
交换二者不影响其他大臣的收益
我们对比交换前后二者的收益:
交换前:i人:premul(i - 1) / bi i + 1人:premul(i - 1) * ai / bi+1
交换后:i人:premul(i - 1) / bi+1 i + 1人:premul(i - 1) * ai+1 / bi
四个数同乘 bi*bi+1/premul(i - 1):
交换前:i人:bi+1 i + 1人:ai bi
交换后:i人:bi i + 1人:ai+1 bi+1
由于ai * bi >= ai+1*bi+1,ai bi >= bi,则交换后整体的最大值没有变大,甚至变小
那么我们交换所有逆序对可以得到不比最优解差的解,故我们的贪心策略正确。
cpp要手写高精度
#include <iostream>
#include <cstring>
#include <vector>
#include <algorithm>
using namespace std;
typedef pair<int, int> PII;
const int N = 1005;vector<int> mul(vector<int>& a, int x){int n = a.size(), t = 0;vector<int> ret;for(int i = 0; i < n; i ++){t += a[i] * x;ret.push_back(t % 10);t /= 10;}while(t) ret.push_back(t % 10), t /= 10;return ret;
}vector<int> div(vector<int>& a, int x){int n = a.size(), t = 0;vector<int> ret;for(int i = n - 1; ~i; i --){t = t * 10 + a[i];ret.push_back(t / x);t %= x;}reverse(ret.begin(), ret.end());while(ret.size() && !ret.back()) ret.pop_back();return ret;
}
vector<int> ma(const vector<int>& a, const vector<int>& b){if(a.size() > b.size()) return a;if(a.size() < b.size()) return b;if(vector<int>(a.rbegin(), a.rend()) > vector<int>(b.rbegin(), b.rend())) return a;return b;
}
int n;
PII w[N];int main(){cin >> n, n ++;for(int i = 0, a, b; i < n; i ++) cin >> a >> b, w[i] = { a, b };sort(w + 1, w + n, [](const PII& a, const PII& b){return a.first * a.second < b.first * b.second;});vector<int> cur(1, 1), res(1, 0);for(int i = 0; i < n; i ++){ if(i)res = ma(res, div(cur, w[i].second));cur = mul(cur, w[i].first);/*for(int x : vector<int>(cur.rbegin(), cur.rend()))cout << x;puts("");*/} for(int x : vector<int>(res.rbegin(), res.rend()))cout << x;return 0;
}
不想写高精度就用python3
n = int(input())
n += 1
w = [tuple(map(int, input().split())) for _ in range(n)]
cur ,res = w[0][0], 0
for a, b in sorted(w[1::], key=lambda x:x[0]*x[1]):res = max(res, cur // b)cur *= a
print(res)
2.11 耍杂技的牛
125. 耍杂技的牛 - AcWing题库
和上一题很像,这题按照w + s升序排序
和上一题同样的证明思路,不再赘述
n = int(input())
ws = [tuple(map(int, input().split())) for _ in range(n)]
pre = 0
ans = -1e18
for w, s in sorted(ws, key=lambda x:x[0]+x[1]):ans = max(ans, pre - s)pre += w
print(ans)
2.12 给树染色
115. 给树染色 - AcWing题库
错误的贪心:从根结点开始扩展,每次取当前最小权值的结点
很容易举出反例,可以自己试一下。
我们可以确定的事情是,当前除去根节点的最大权值结点会在其父节点被染色后立即被染色。
那么我们考虑当前最大结点x,父节点y,和任意结点z,染色顺序无非:
x,y,z,代价为x + 2y + 3z
z,x,y,代价为:z + 2x + 3y
二者做差有:2z - (x + y),可见当z大于x+y的平均值时才会先染x+y
那么我们在考虑当前树中剩余结点时,不妨将x,y当成一个结点,其权值为平均权值,然后就有了做法:
选择当前树中的最大权值,进行染色,由于它和父亲染色顺序为一前一后,所以染色后合并到父亲结点后面
我们合并n - 1次就只剩下一个结点,此时整棵树的染色顺序也就知道了
具体实现时,由于我们并不关心具体染色方案,所以为了简便,我们可以在合并时维护答案
考虑x合并到y上,由于要先染色y,所以x的权值要被加上y的sz次(sz为y结点的大小)
可以用并查集+堆优化到O(nlogn),不过这个数据量没必要,重要的还是这道题的思想
#include <iostream>
#include <algorithm>
#include <cstring>
using namespace std;const int N = 1005;
const double eps = 1e-6;
struct node{int fa, sz, v;double avg;
}nodes[N];
int n, root, res;int nxt()
{double avg = 0;int res = -1;for (int i = 1; i <= n; i ++ )if (i != root && nodes[i].avg > avg){avg = nodes[i].avg;res = i;}return res;
}int main(){cin >> n >> root;for(int i = 1, v; i <= n; i ++){cin >> v, res += v;nodes[i] = { -1, 1, v, v };}for(int i = 1, a, b; i < n; i ++){cin >> a >> b;nodes[b].fa = a;}for(int i = 1; i < n; i ++){int t = nxt(), fa = nodes[t].fa;res += nodes[fa].sz * nodes[t].v;nodes[t].avg = -1;for(int j = 1; j <= n; j ++)if(nodes[j].fa == t) nodes[j].fa = fa;nodes[fa].sz += nodes[t].sz, nodes[fa].v += nodes[t].v, nodes[fa].avg = (double)nodes[fa].v / nodes[fa].sz;}cout << res;return 0;
}
2.13 任务
127. 任务 - AcWing题库
我们发现式子中x对于利润占主导,所以按x从大到小来进行考虑每个任务。对于每个任务从时间满足的机器中选择等级足够且最小的那个。
具体流程如下:
- 按照x对任务和机器排序
- 按x从大到小遍历任务,把时间充足的机器放入集合
- 如果集合中存在等级足够的机器,那么选择等级最小的那个
- 再处理下一个任务时,集合中的机器的时间都是足够的,我们只需考虑等级
时间复杂度:O(nlogn + mlogn)
#include <bits/stdc++.h>
using i64 = long long;
using PII = std::pair<int, int>;
const int N = 1e5 + 10, M = 1e5 + 10;
int n, m;
PII a[N], b[M];
int main(){std::ios::sync_with_stdio(false), std::cin.tie(0), std::cout.tie(0);while (std::cin >> n >> m){for(int i = 0; i < n; i ++) std::cin >> a[i].first >> a[i].second;for(int i = 0; i < m; i ++) std::cin >> b[i].first >> b[i].second;std::sort(a, a + n), std::sort(b, b + m);std::multiset<int> st;i64 cnt = 0, res = 0;for(int i = m - 1, j = n - 1; ~i; i --){while(~j && a[j].first >= b[i].first)st.insert(a[j --].second);auto it = st.lower_bound(b[i].second);if(it != st.end()){cnt ++;res += 500 * b[i].first + 2 * b[i].second;st.erase(it);}}std::cout << cnt << ' ' << res << '\n';}return 0;
}
2.14 能量石
734. 能量石 - AcWing题库
01背包 + 临项交换
先暴力考虑所有情况,即全排列中依次求01背包
那么最优解是否存在某种特性呢?或者说,我们需要考虑的情况的范围能否缩小?
我们考虑最优解,相邻两个能量石s[i], s[i + 1]
二者的收益为:e’[i] + e’[i + 1] - s[i] * l[i + 1]
交换次序:e’[i] + e’[i + 1] - s[i + 1] * l[i]
由于是最优解,所以交换前的收益不小于交换后的收益:s[i] * l[i + 1] <= s[i + 1] * l[i]
那么说明最优解满足两两之间s[i] * l[i + 1] <= s[i + 1] * l[i]
所以我们将能量石按照s[i] / l[i]升序排序,然后跑01背包即可
#include <bits/stdc++.h>
#define sc scanf
using i64 = long long;
const int N = 105, M = 1e4 + 10;
struct node{int s, e, l;bool operator<(const node& x) const{return s * x.l < x.s * l;}
}nodes[N];int main(){int _ = 1;std::cin >> _;for(int t = 1, n, m; t <= _; t ++){std::cin >> n;m = 0;for(int i = 0, a, b, c; i < n; i ++) std::cin >> a >> b >> c, nodes[i] = { a, b, c }, m += a;std::sort(nodes, nodes + n);std::vector<i64> f(m + 1, -1e8);f[0] = 0;for(int i = 0; i < n; i ++){auto [s, e, l] = nodes[i];for(int j = m; j >= s; j --){f[j] = std::max(f[j], f[j - s] + e - (j - s) * l);}}printf("Case #%d: %lld\n", t, *std::max_element(f.begin(), f.end()));}return 0;
}
三、总结
很想从上面的问题中提取出某些东西,但是发现没有套路可言,只是遇到贪心问题时有了几个贪心的方向,区间类试着按端点排序,贪心构造,临项交换等等,但具体还得多做题。
相关文章:

基础算法,贪心算法,贪心策略,OJ练习
文章目录 一、概念二、OJ练习2.1 区间选点2.2 区间合并2.3 区间2.4 合并果子2.5 排队接水2.6 货仓选址2.7 防晒2.8 畜栏预定2.9 雷达设备2.10 国王游戏2.11 耍杂技的牛2.12 给树染色2.13 任务2.14 能量石 三、总结 一、概念 贪心是一种在每次决策时采取当前意义下最优策略的算…...
一文讲透亚马逊云三层架构
关于三层架构,我们有很多想说的话: (以下内容以下都在VPC中) cloudfront做CDN加速网关规划S3做静态网站托管APIGateway作为统一网关入口认证/限流Lambda 作为传统后端,并发,底层架构Redis缓存DDB作为持久化…...

只需3步,使用Stable Diffusion无限生成AI数字人视频(附安装包)
基本方法 搞一张照片,搞一段语音,合成照片和语音,同时让照片中的人物动起来,特别是头、眼睛和嘴。 语音合成 语音合成的方法很多,也比较成熟了,大家可以选择自己方便的,直接录音也可以&#…...
之小部件(七):如何使用图像image部件来显示图片?)
RustGUI学习(iced)之小部件(七):如何使用图像image部件来显示图片?
前言 本专栏是学习Rust的GUI库iced的合集,将介绍iced涉及的各个小部件分别介绍,最后会汇总为一个总的程序。 iced是RustGUI中比较强大的一个,目前处于发展中(即版本可能会改变),本专栏基于版本0.12.1. 概述 这是本专栏的第七篇,主要讲述图像Image部件的使用,会结合实例…...

Substrate 入门课第 14 期圆满结束,岗位内推直达知名 Web3 项目!
Substrate,一个完全免费且开源的框架,利用 Rust 语言的强大功能和安全性,为全球开发者提供了一个高效和灵活的开发环境。借助其模块化的设计,即使是新手开发者也能在短短 15 分钟内搭建起定制化的区块链。自 2020 年以来ÿ…...
android进阶-AIDL
参考:Android进阶——AIDL详解_android aidl-CSDN博客 AIDL(Android 接口定义语言),可以使用它定义客户端与服务端进程间通信(IPC)的编程接口,在 Android 中,进程之间无法共享内存&…...

贪心算法-活动选择问题背包问题
目录 活动选择问题 无重叠区间-Leetcode 435 分数背包问题--贪心解法 贪心法 0-1 背包问题 贪心法 贪心算法的局限 Set cover problem 活动选择问题 分析: /* 要在一个会议室举办n个活动 - 每个活动有它们各自的起始和结束时间 - 找出在时间上互不冲突的活动组合,能…...

Web3工具集合 - 00
使用 React 和 Material-UI 构建的 Web3 工具集合 大家好! 我很高兴向大家介绍我最近刚启动了一个项目:Web3 工具集合。 这个项目的目的是一个集成各种 Web3 工具的网站,旨在为开发人员和加密货币爱好者提供便捷的工具和资源。 特点&#…...
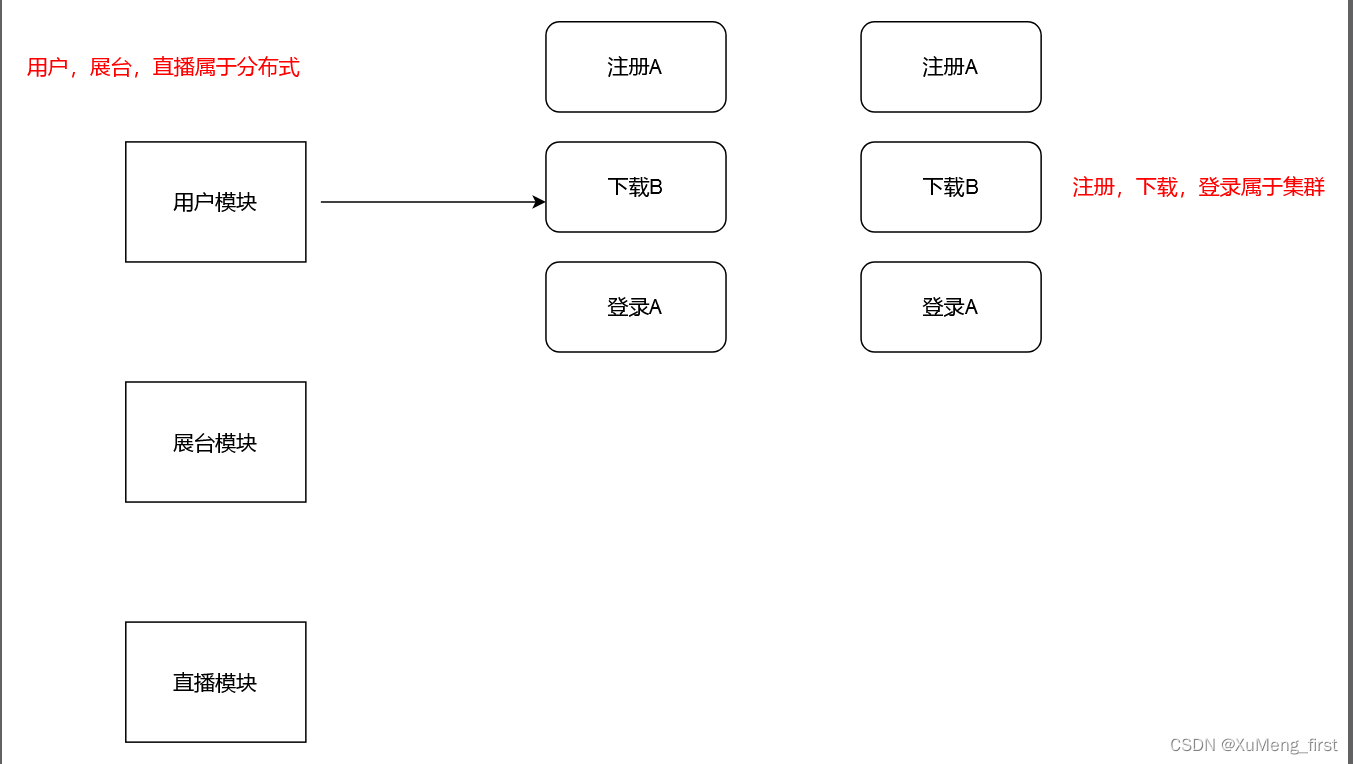
分布式与集群的区别
先说区别: 分布式是并联工作的,集群是串联工作的。 分布式中的每一个节点都可以做集群。而集群并不一定就是分布式的。 集群举例:比如新浪网,访问的人很多,他可以做一个集群,前面放一个相应的服务器&…...

学习心得:如何开始学习一款MCU
一、MCU简介 任何一款MCU,其基本原理和功能都是大同小异,所不同的只是其外围功能模块的配置及数量、指令系统等。对于指令系统,虽然形式上看似千差万别,但实际上只是符号的不同,其所代表的含义、所要完成的功能和寻址…...
顺序表的实现(迈入数据结构的大门)(1)
上一节我们认识到了什么是数据结构 这一节我们就来实现第一个数据结构的实现 思考一个问题: 假定一个数组,空间为10,已经使用了5个,向其中插入数据的步骤: 1.插入数据,我们先要求数组长度,其…...
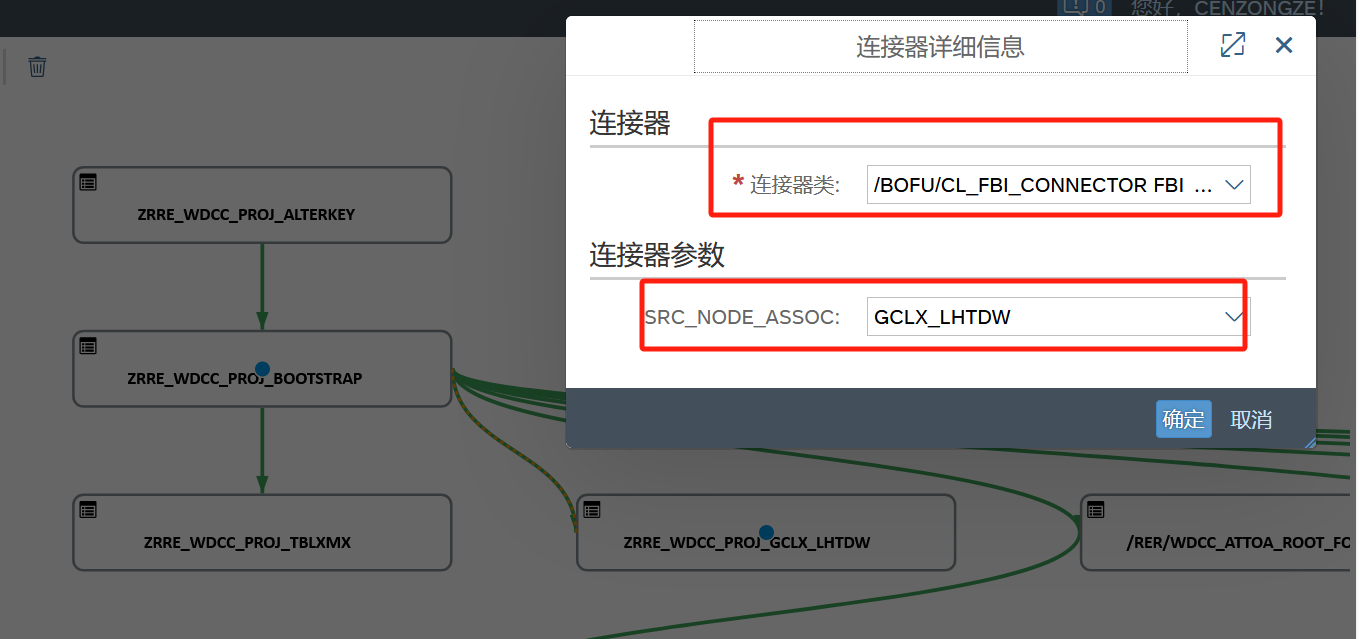
RERCS系统-WDA+BOPF框架实战例子 PART 1-新建List UIBB(列表组件)并分配Feeder Class和Node Element
需求背景: 已有的项目主数据功能,新增一个列表UIBB显示主数据额外的关联数据明细。 1、Fiori页面通过右键-技术帮助打开对应的组件配置; 2、双击对应的组件配置,调整对应的页面新建UIBB; 3、填写对应的UIBB属性字段&a…...

如何从 iPhone 恢复已删除或丢失的联系人?
不小心删除了您的 iPhone 联系人?不用担心。我们将向您展示如何从 iPhone或 iPad恢复已删除或丢失的联系人。当您从 iPhone 中删除联系人时,您可能认为无法将其恢复。但事实是,您可以从 iPhone 或 iPad 恢复已删除的联系人,因为它…...

RISCV 外部GCC 工具链安装@FreeBSD15
在交叉编译的时候,可以使用FreeBSD15默认的工具链:LLVM 也可以使用GCC工具链,GCC可以使用现成pkg包安装,也可以编译安装。 LLVM的特点是高移植性和高效,但学习成本高。GCC的特点是成熟稳定,但优化能力有限…...

全栈开发之路——前端篇(9)插槽、常用api和全局api
全栈开发一条龙——前端篇 第一篇:框架确定、ide设置与项目创建 第二篇:介绍项目文件意义、组件结构与导入以及setup的引入。 第三篇:setup语法,设置响应式数据。 第四篇:数据绑定、计算属性和watch监视 第五篇 : 组件…...

减瘦误区、雷点、陷阱和挑战怎么应对
在减瘦过程中,很多肥胖人群都容易踩到坑。比如陷入误区,认为只有短期快速的减调方式方法,才值得尝试,而忽视身体健康;或是踩到雷点,轻信强速方剂或方法,结果身体产生了排斥或根本没效用白花钱&a…...

Leetcode—946. 验证栈序列【中等】
2024每日刷题(133) Leetcode—946. 验证栈序列 实现代码 class Solution { public:bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {int left 0;for(int i 0; i < popped.size(); i) {while(left &…...

Selenium定位方法及代码
天行健,君子以自强不息;地势坤,君子以厚德载物。 每个人都有惰性,但不断学习是好好生活的根本,共勉! 文章均为学习整理笔记,分享记录为主,如有错误请指正,共同学习进步。…...

GitHub搭建免费博客
一、GitHub仓库准备 搭建博客需要准备两个仓库。一个存放博客图床的仓库,另一个存放博客网站的仓库。 1.1、图床创建 新建仓库 第一步: 第二步: 生成Token令牌 点击右上角头像->Settings->下拉,直到左侧到底&#…...
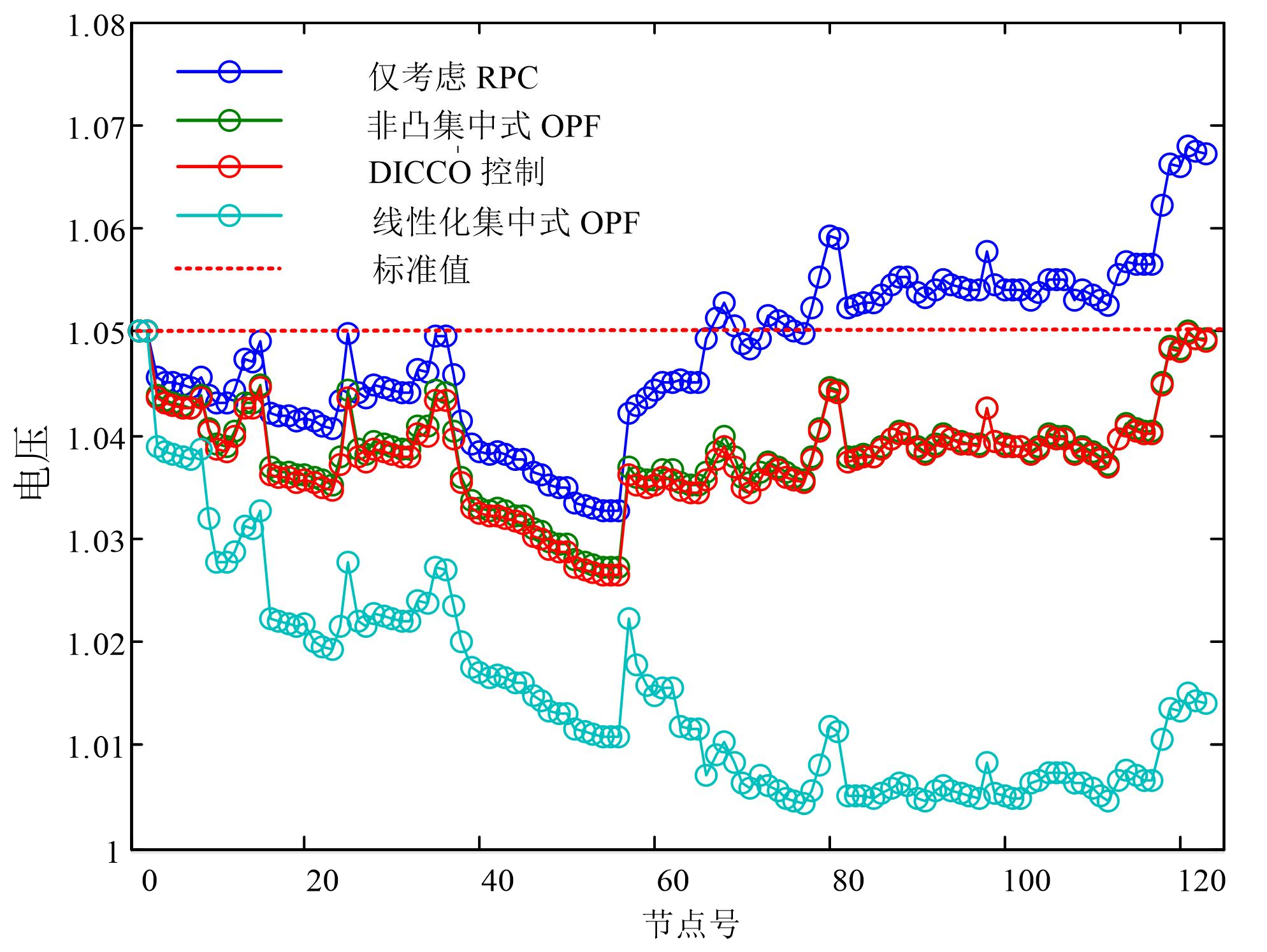
开源代码分享(28)-含分布式光伏的配电网集群划分和集群电压协调控制
参考文献: [1] Chai Y , Guo L , Wang C ,et al.Network Partition and Voltage Coordination Control for Distribution Networks With High Penetration of Distributed PV Units[J].IEEE Transactions on Power Systems, 2018:3396-3407.DOI:10.1109/TPWRS.2018…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...
)
OpenLayers 分屏对比(地图联动)
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 地图分屏对比在WebGIS开发中是很常见的功能,和卷帘图层不一样的是,分屏对比是在各个地图中添加相同或者不同的图层进行对比查看。…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
