逻辑优化基础-shannon decomposition
1. 简介
在逻辑综合中,香农分解(Shannon decomposition)是一种常用的布尔函数分解方法。它将一个布尔函数分解为两个子函数的和,其中每个子函数包含一个布尔变量的取反和非取反的部分。
具体来说,假设对于一个布尔函数 F(x1,x2,...,xn)F(x_1, x_2, ..., x_n)F(x1,x2,...,xn)
进行香农分解,首先选定进行分解的变量,假设为xkx_kxk,则该香农分解可以表示为:
F(x1,x2,...,xn)=xk∗Fk(x1,x2,...,xn,xk=1)+xk′∗Fk′(x1,x2,...,xn,xk=0)F(x_1, x_2, ..., x_n) = \\ x_k * F_k(x_1, x_2, ..., x_n, x_k=1) + x'_k * F_k'(x_1, x_2, ..., x_n, x_k=0) F(x1,x2,...,xn)=xk∗Fk(x1,x2,...,xn,xk=1)+xk′∗Fk′(x1,x2,...,xn,xk=0)
其中,xkx_kxk 是函数 FFF 的一个输入变量,xk′x'_kxk′ 是 xkx_kxk 的取反,FkF_kFk 是当 xk=1x_k=1xk=1 时 FFF 的取值为真时的部分函数,Fk′F_k'Fk′ 是当 xk=0x_k=0xk=0 时 FFF 的取值为真时的部分函数。
这个分解的意义在于,它将一个布尔函数 FFF 分解成了两个子函数 FkF_kFk 和 Fk′F_k'Fk′,这两个子函数相互独立,因为它们只与 FFF 的一个输入变量 xkx_kxk 有关。这种分解可以用于减少门电路的复杂度,从而实现更快的逻辑运算和更小的电路面积,如何拿到更小的面积,后续了解到了再补充,本文主要是得到更快的速度。
香农分解的基本思想可以进一步扩展到多个输入变量的情况,即将一个布尔函数 F(x1,x2,...,xn)F(x_1, x_2, ..., x_n)F(x1,x2,...,xn) 分解成两个子函数 F0 和 F1,其中 F0 和 F1 分别只与 x1x_1x1 取 0 和 1 时的输入变量 x2,x3,...,xnx_2, x_3, ..., x_nx2,x3,...,xn 有关。这种扩展的香农分解方法被称为递归香农分解(Recursive Shannon Decomposition),在实际的逻辑综合和电路设计中得到了广泛的应用。
2. 示例
假设有一个函数:
F=(a,b,c,x)F = (a, b, c, x) F=(a,b,c,x)
以变量 xxx 进行分解,则可以得到以下表达式:
F=x.(a,b,c,1)+x′.F(a,b,c,0)F = x.(a, b, c, 1) + x′.F(a, b, c, 0) F=x.(a,b,c,1)+x′.F(a,b,c,0)
如果用电路图来表示以上分解的话,如下所示:
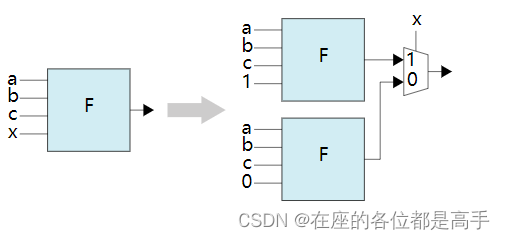
更近一步,常数的信号通常可以被优化掉,变成以下的结构:
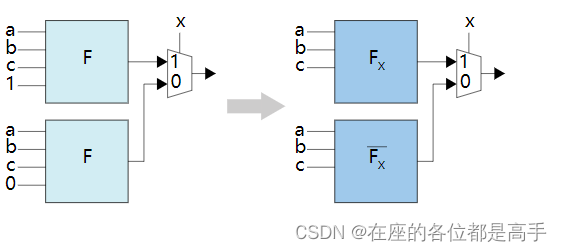
我们可以看到,经过香农分解后,信号 xxx 距离输出 outputoutputoutput 最近,xxx 所在的路径是整个 logic cone 中最快的一条。
所以说如果在电路 output required time 确定的情况下,某一个信号的 arrival time 非常的晚,可以把这个信号向靠近output的方向 push,从而降低电路的延迟。
这种做法的缺点也是显而易见的,至少在这个例子中,面积几乎一直出于增长的状态。
按照上面简介部分介绍的递归香农分解继续执行的话,可以得到如下电路:
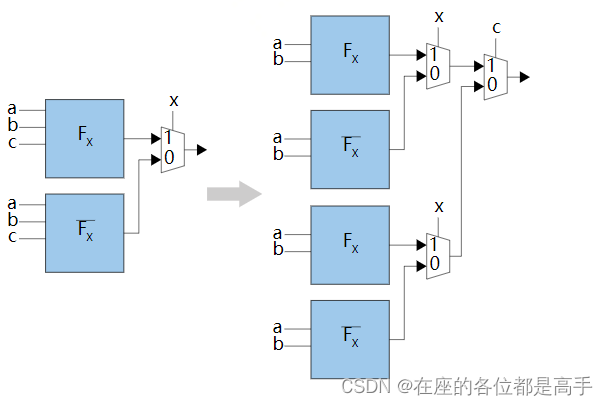
2.1 个人理解
做timing优化的时候主要是将那些 arrival time 比较慢的信号尽可能的往 output 推,所以也就是说要基于这些 arrival time慢的信号进行香农分解。
3. 特殊案例(pipeline loop)
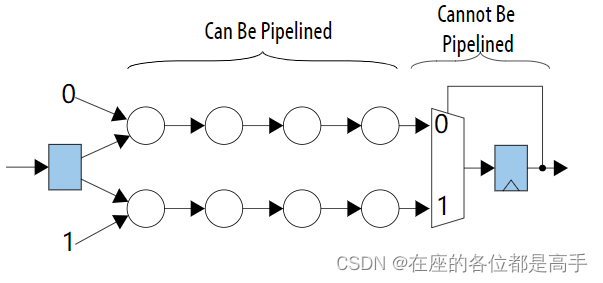
香农分解是优化电路中 looplooploop 的一种有效技术。当你对 looplooploop 中的逻辑执行香农分解时,looplooploop 中的逻辑会移动到 looplooploop 外部。从而可以对移动到循环外部的逻辑进行 pipelinepipelinepipeline 处理。
假设有以下一个 looplooploop 电路,因为是在一个 looplooploop 里面,所以这一部分信号不能进行 pipelinepipelinepipeline:
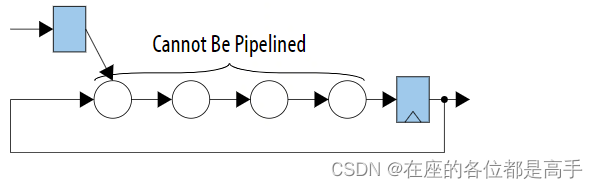
该电路有一个单独的 registerregisterregister 和一个额外的输出,我们可以通过执行香农分解将这个 looplooploop 的逻辑移动到外部以进行 pipelinepipelinepipeline,具体的做法如下:
我们知道 registerregisterregister outputoutputoutput的值只能为 0 或者 1,所以我们可以将驱动 registerregisterregister 的逻辑复制(duplicate)一份,一份 registerregisterregister 的输入为 000, 一份为 111,即对于这个outputoutputoutput 进行香农分解,即可得到以下的电路:
相关文章:

逻辑优化基础-shannon decomposition
1. 简介 在逻辑综合中,香农分解(Shannon decomposition)是一种常用的布尔函数分解方法。它将一个布尔函数分解为两个子函数的和,其中每个子函数包含一个布尔变量的取反和非取反的部分。 具体来说,假设对于一个布尔函…...

Java中线程池的创建与使用
前言:默认线程池的弊端在线程池应用中,参考阿里巴巴java开发规范:线程池不允许使用Executors去创建,不允许使用系统默认的线程池,推荐通过ThreadPoolExecutor的方式,这样的处理方式让开发的工程师更加明确&…...

关于HashMap与OkHttp的使用
写了一个okhttp的post请求方法,添加参数很麻烦,需要封装: //post请求public static void sendOkHttpRequestPost(String address , Callback callback) {OkHttpClient client new OkHttpClient();// 创建表单参数RequestBodyRequestBody fo…...
【独家】)
华为OD机试 - 单词倒序(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:单词倒序…...
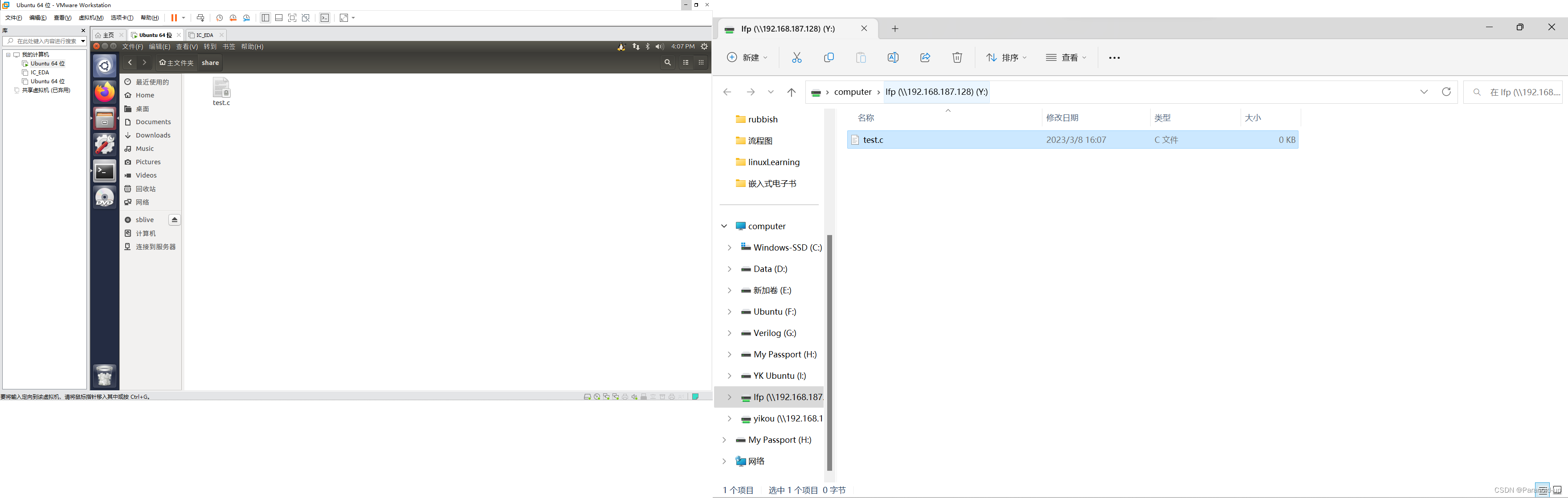
搭建Samba服务器
搭建Samba服务器 文章目录搭建Samba服务器samba安装安装命令配置-ubuntu侧为samba服务器创建一个共享目录share创建使用该共享文件夹的账号修改samba服务器配置文件重启samba服务windows创建映射1.点击映射网络驱动器2.输入Ubuntu中的ip地址及其用户信息3.输入用户信息及其密码…...
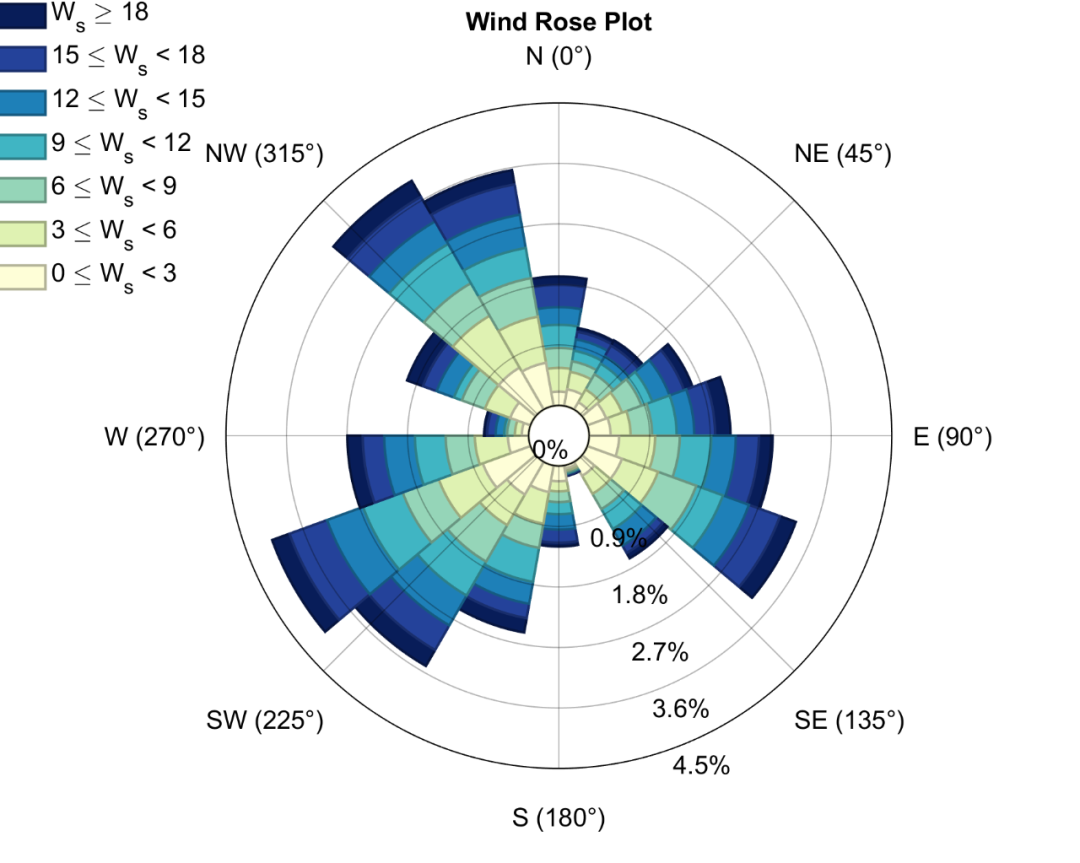
Matlab进阶绘图第5期—风玫瑰图(WindRose)
风玫瑰图(Wind rose diagram)是一种特殊的极坐标堆叠图/统计直方图,其能够直观地表示某个地区一段时期内风向、风速的发生频率。 风玫瑰图在建筑规划、环保、风力发电、消防、石油站设计、海洋气候分析等领域都有重要作用,所以在一些顶级期刊中也能够看…...
:数仓报表场景☞通过执行计划详解”行转列”,”列转行”是如何实现的)
【SQL开发实战技巧】系列(二十四):数仓报表场景☞通过执行计划详解”行转列”,”列转行”是如何实现的
系列文章目录 【SQL开发实战技巧】系列(一):关于SQL不得不说的那些事 【SQL开发实战技巧】系列(二):简单单表查询 【SQL开发实战技巧】系列(三):SQL排序的那些事 【SQL开发实战技巧…...
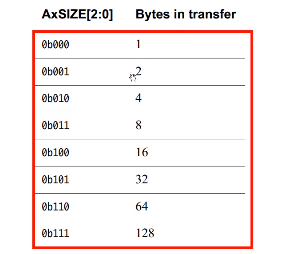
XILINX AXI总线学习
AXI介绍什么是AXI?AXI(高级可扩展接口),是ARM AMBA的一部分;AMBA:高级微控制器总线架构;是1996年首次引入的一组微控制器总线;开放的片内互联的总线标准,能在多主机设计中实现多个控…...

2022CCPC女生赛(补题)(A,C,E,G,H,I)
迟了好久的补题,,现在真想把当时赛时的我拉出来捶一拳排序大致按照题目难度。C. 测量学思路:直接循环遍历判断即可,注意角度要和2π取个最小值。AC Code:#include <bits/stdc.h>typedef long long ll; const int…...

【Nginx】Nginx的安装配置
环境说明系统:Centos 7一、编译安装Nginx官网下载地址nginx: download#安装依赖 [rootnginx nginx-1.22.1]# yum install gcc pcre pcre-devel zlib zlib-devel -y #从官网下载Nginx安装包,并进行解压、编译、安装 [rootnginx ~]# wget https://nginx.or…...

数学小课堂:统计时有效地筛选数据
文章目录引言I 被爆冷门的原因II 统计时有效地筛选数据2.1 统计数据的常见问题2.2 大数据的特征2.3 有效筛选数据的原则引言 在博弈论中很多结果有发生的概率,而概率这件事只是估计出来的,并不准确。因此,一旦加入博弈的选手多了之后&#x…...

MySQL安装优化
hello,大家好,我是小鱼 本文主要通过针对 MySQL Server(mysqld)相关实现机制的分析,得到一些相应的优化建议。主要 涉及 MySQL 的安装以及相关参数设置的优化,但不包括 mysqld 之外的比如存储引擎相关的参…...

RocketMQ系列开篇
RocketMQ系列开篇 今天开始学习RocketMQ相关系列源码。我会带着自己的目的去学习源码。所以不会像一般的技术博客一样,写一个完整的流程,介绍每一步干了啥。而是提出一个问题,然后去看代码里面是怎么实现的。说明一下,本次系列我…...
logback无法删除太久远的日志文件?logback删除日志文件源码分析
logback无法删除太久远的日志文件?logback删除日志文件源码分析 最近发现logback配置滚动日志,但是本地日志文件甚至还有2年前的日志文件,服务器是却是正常的! 网上搜索了一波没有发现,只找到说不能删除太久远的旧日志…...

【MyBatis-Plus】基于@Version注解的乐观锁实现
引入mybatis-plus依赖,注意这里的版本要求 since 3.4.0;(3.4.1,3.4.2已测) 3.2.0肯定是不支持的,无法引入MybatisPlusInterceptor; 乐观锁 当要更新一条记录的时候,希望这条记录没有被别人更新…...
ubuntu20.04搭建detectron2环境
Ubuntu22.04安装Cuda11.3 Linux下驱动安装 # 以下命令按顺序执行 sudo apt update && sudo apt upgrade -y # or sudo apt update # 查看显卡信息 ubuntu-drivers devices sudo ubuntu-drivers autoinstall # or sudo apt install nvidia-driver-510 reboot nvidia-s…...
Navicate远程连接Linux上docker安装的MySQL容器
Navicate远程连接Linux上docker安装的MySQL容器失败 来自:https://bluebeastmight.github.io/ 问题描述:windows端的navicat远程连接不上Linux上docker安装的mysql(5.7版本)容器,错误代码10060 标注: 1、…...
基于Jetson NX的模型部署
系统安装 系统安装过程分为3步: 下载必要的软件及镜像 Jetson Nano Developer Kit SD卡映像 https://developer.nvidia.com/jetson-nano-sd-card-image Windows版SD存储卡格式化程序 https://www.sdcard.org/downloads/formatter_4/eula_windows/ 镜像烧录工具…...
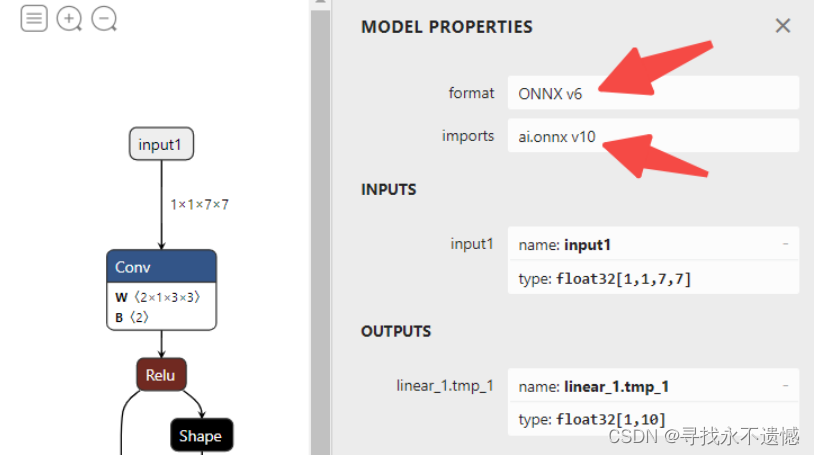
【PaddlePaddle onnx】PaddlePaddle导出ONNX及模型可视化教程
文章目录1 背景介绍2 实验环境3 paddle.onnx.export函数简介4 代码实操4.1 PaddlePaddle与ONNX模型导出4.2 ONNX正确性验证4.3 PaddlePaddle与ONNX的一致性检查4.4 多输入的情况5 ONNX模型可视化6 ir_version和opset_version修改7 致谢原文来自于地平线开发者社区,未…...

虹科案例 | 如何可持续的对变压器进行温度监控?
为了延长变压器的使用寿命,需要一个测量系统来监测内部整个绕组区域的温度。它必须明确温度升高发生的位置及其强度。您可以在此处了解为什么会这样以及如何在实践中实施? PART 1 变压器多点测温问题 变压器的工作温度越高,使用寿命越短。这里主要存在…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

在web-view 加载的本地及远程HTML中调用uniapp的API及网页和vue页面是如何通讯的?
uni-app 中 Web-view 与 Vue 页面的通讯机制详解 一、Web-view 简介 Web-view 是 uni-app 提供的一个重要组件,用于在原生应用中加载 HTML 页面: 支持加载本地 HTML 文件支持加载远程 HTML 页面实现 Web 与原生的双向通讯可用于嵌入第三方网页或 H5 应…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

Java毕业设计:WML信息查询与后端信息发布系统开发
JAVAWML信息查询与后端信息发布系统实现 一、系统概述 本系统基于Java和WML(无线标记语言)技术开发,实现了移动设备上的信息查询与后端信息发布功能。系统采用B/S架构,服务器端使用Java Servlet处理请求,数据库采用MySQL存储信息࿰…...
