各种激活函数的计算公式、图像以及实现代码
激活函数已经成为神经网络中非常重要的一部分,随着各种类型的神经网络模型被人们开发出来,各种激活函数也应运而生,在不同的场景中,取得良好的效果。本文跟据著名的YOLO系列目标检测模型的源码 AlexeyAB Darknet,整理出目前神经网络模型中应用最广泛的20种激活函数,对它们的计算公式、图像特点进行介绍,并使用python代码实现这些激活函数的计算。
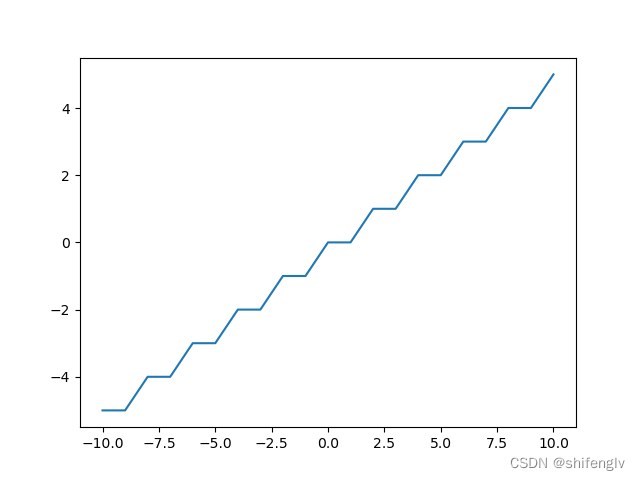
1、stair激活函数
如图1所示,stair激活函数的图像就像阶梯一样。它的计算公式如下:
式子中,表示不大于x的整数,
表示对2取余数。
代码实现如下:
def stair(x):n=math.floor(x)if n%2==0:return math.floor(x/2.0)else:return (x-n)+math.floor(x/2.0)2、hardtan激活函数
如图2所示,hardtan激活函数是通过以直代曲近似实现tan函数,其计算公式如下:

代码实现如下:
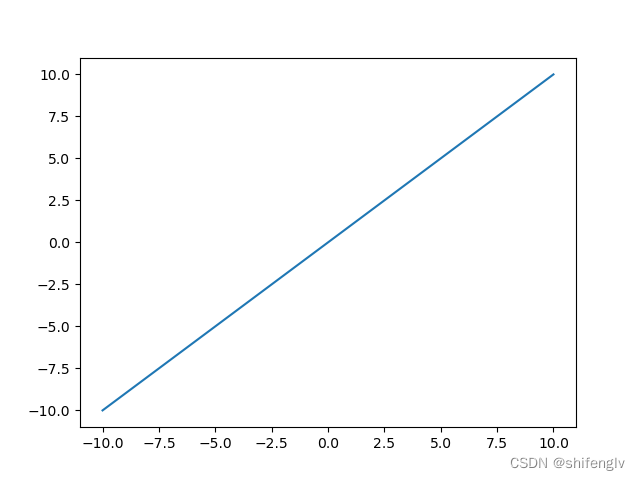
def hardtan(x):if x<-1.0:return -1.0elif x>1.0:return 1.0else:return x3、linear激活函数
linear激活函数是线性激活函数,输入x输出也是x,其函数图像如图3所示。
代码实现:
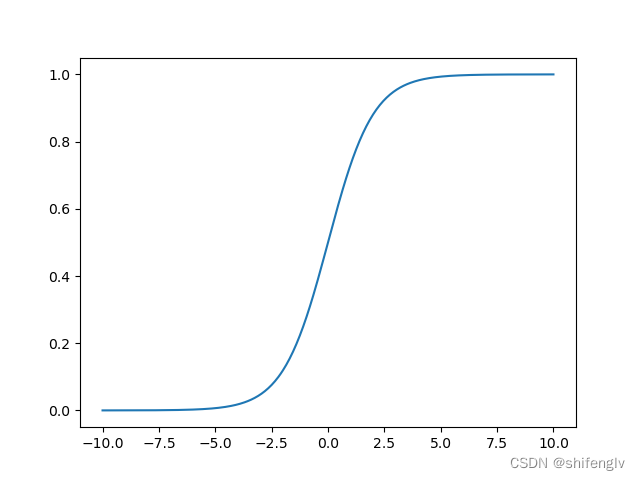
def linear(x):return x4、logistic激活函数
logistic激活函数又叫sigmoid激活函数,如图4所示,logistic函数可以结果映射到0到1之间。其计算公式如下:
代码实现如下:
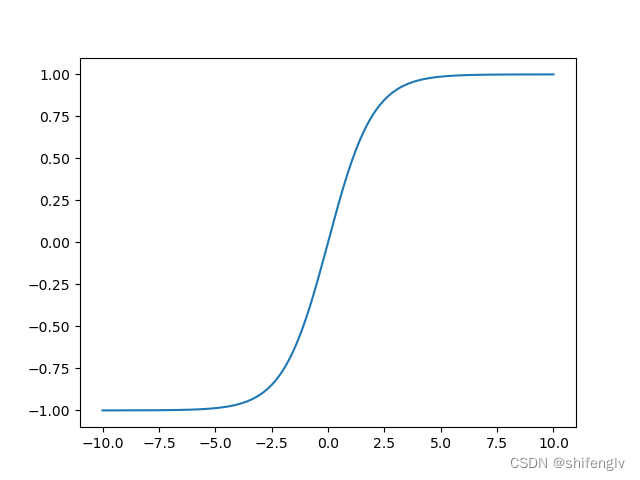
def logistic(x):return 1.0/(1.0+math.exp(-x))5、loggy激活函数
如图5所示,loggy的函数图像跟logistic有点相似,也是把输出映射到0到1之间。其计算公式如下:
代码实现:
def loggy(x):return 2.0/(1.0+math.exp(-x))-1.06、relu激活函数
relu激活函数为线性整流函数,目的是把小于0的数截取掉,其函数图像如图6所示,其计算公式如下:
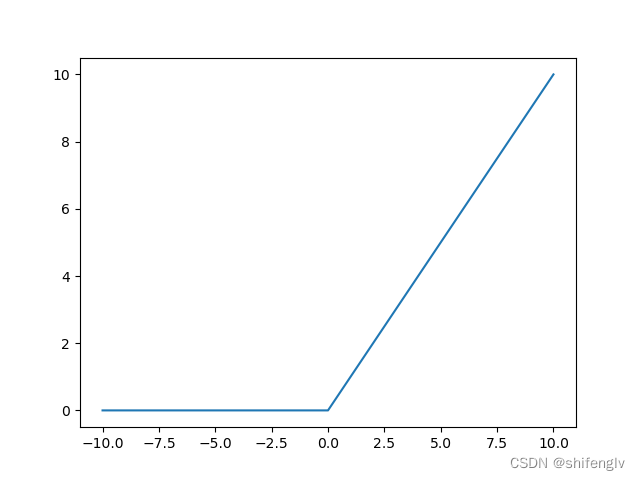
代码实现如下:
def relu(x):return x*(x>0)7、relu6激活函数
relu6和relu一样,也是线性整流函数,不同的是他对大于6的数进行了截断,其函数图像如图7所示,其计算公式如下:
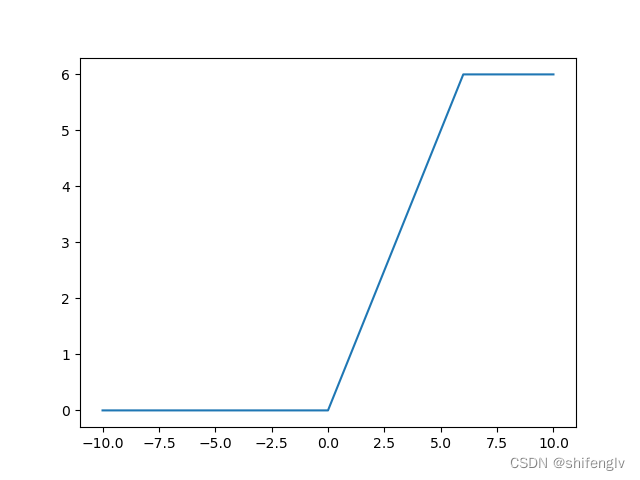
代码实现如下:
def relu6(x):if x<0:return 0.0elif x>6:return 6.0else:return x8、elu激活函数
elu激活函数的图像如图8所示,其计算公式如下:
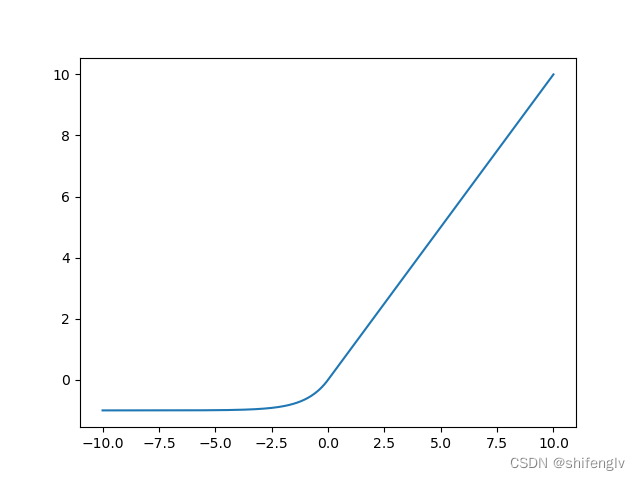
代码实现:
def elu(x):return (x>=0)*x+(x<0)*(math.exp(x)-1.0)9、selu激活函数
selu激活函数如图9所示,其计算公式如下:
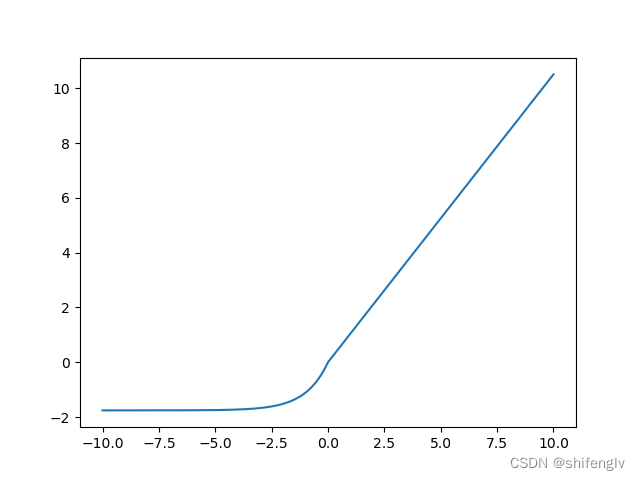
代码实现:
def selu(x):return (x>=0)*1.0507*x+(x<0)*1.0507*1.6732*(math.exp(x)-1.0)10、relie激活函数
相比于relu激活函数,relie激活函数对于小于零的数据并不会直接截取为0,二是乘以一个小的系数,这个系数为0.01。其函数图像如图10所示,其计算公式如下:

代码实现:
def relie(x):if x>0:return xelse:return 0.01*x11、ramp激活函数
如图11所示为ramp激活函数,其计算公式如下:
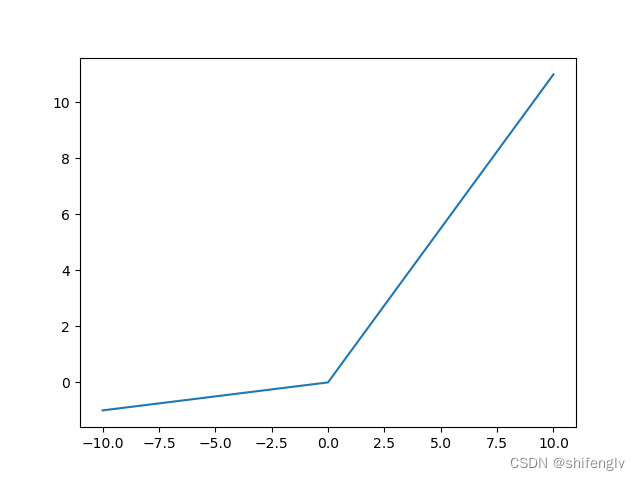
代码实现:
def ramp(x):return x*(x>0)+0.1*x12、leaky激活函数
如图12所示为leaky激活函数的图像,它与relie函数有点像,它的斜率系数要比relie激活函数要大,其计算公式如下:
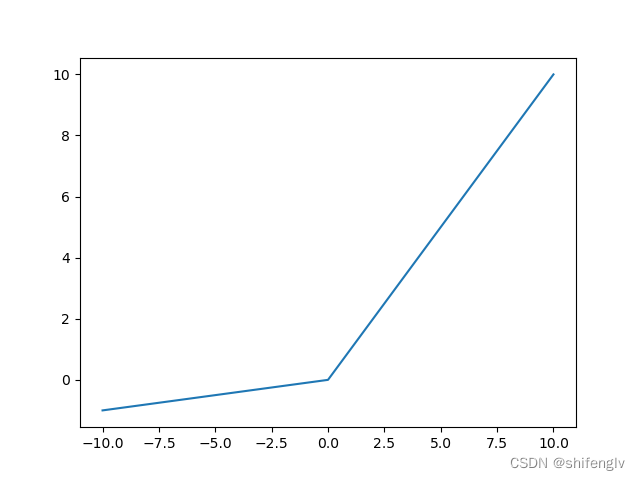
代码实现如下:
def leaky(x):if x<0:return 0.1*xelse:return x13、tanh激活函数
tanh激活函数的图像如图13所示,它的取值范围是[-1,1],其计算公式如下:

代码实现:
def tanh(x):return 2.0/(1.0+math.exp(-2.0*x))-1.014、gelu激活函数
gelu激活函数的图像如图14所示,其计算公式如下:
式中,tanh为上文提到过的激活函数。
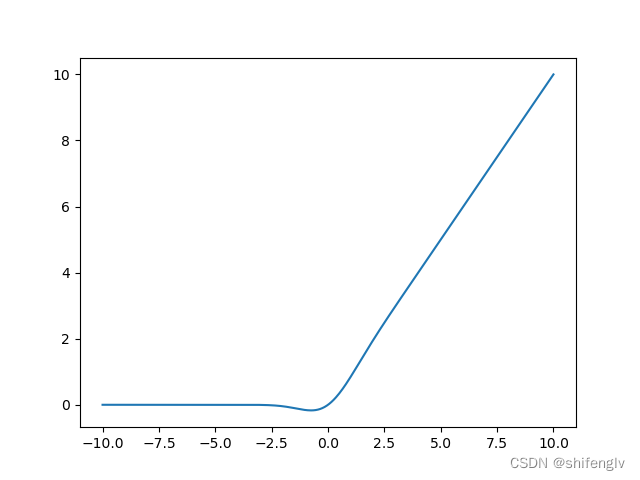
代码实现如下:
def gelu(x):return 0.5*x*(1.0+math.tanh(0.797885*x+0.035677*math.pow(x,3.0)))15、softplus激活函数
softplus激活函数的图像如图15所示,其计算公式如下:
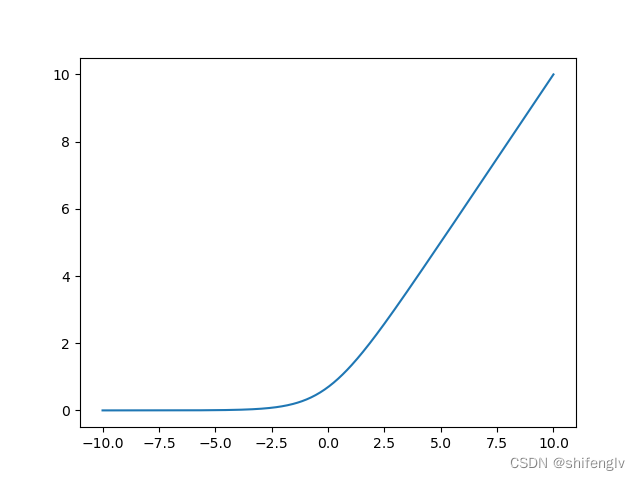
代码实现:
def softplus(x,threshold):if x>threshold:return xelif x<-threshold:return math.exp(x)else:return math.log(math.exp(x)+1.0)16、plse激活函数
图16位plse激活函数的图像,其计算公式如下:

代码实现:
def plse(x):if x<-4:return 0.01*(x+4.0)elif x>4:return 0.01*(x-4.0)+1.0else:return 0.125*x+0.517、lhtan激活函数
图17是lhtan激活函数的图像,其计算公式为:

代码实现:
def lhtan(x):if x<0:return 0.001*xelif x>1:return 0.001*(x-1.0)+1.0else:return x18、swish激活函数
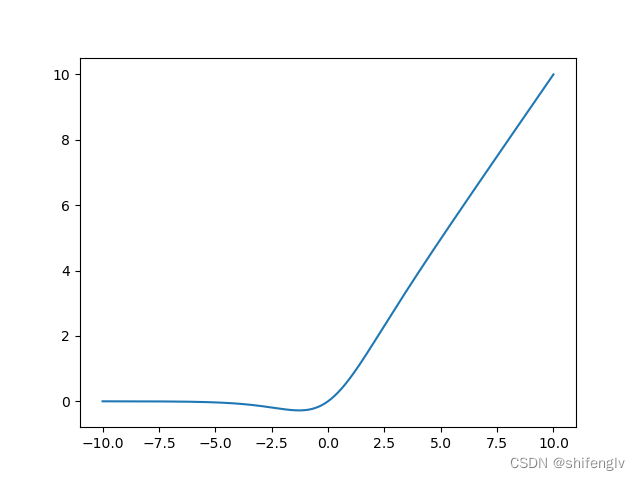
图18是swish激活函数的图像,其计算公式如下:
式中,logistic为上文所提到的激活函数,也叫sigmoid激活函数。
代码实现:
def logistic(x):return 1.0/(1.0+math.exp(-x))def swish(x):return x*logistic(x)19、mish激活函数
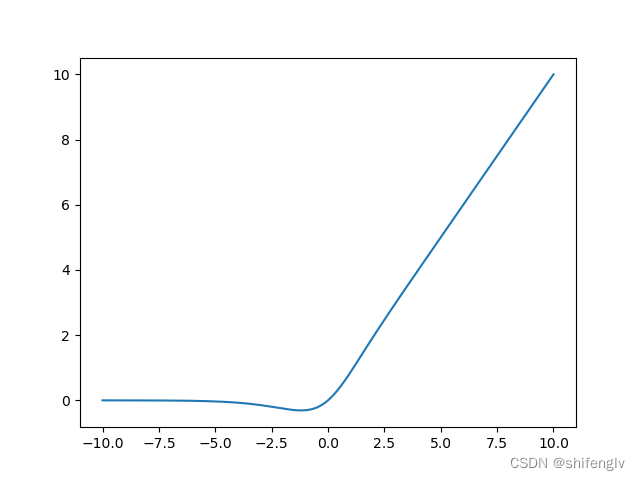
mish激活函数的图像如图19所示,其计算公式如下:
式中tanh,softplus均为上文描述过的激活函数。
代码实现如下:
def softplus(x,threshold):if x>threshold:return xelif x<-threshold:return math.exp(x)else:return math.log(math.exp(x)+1.0)def tanh(x):return 2.0/(1.0+math.exp(-2.0*x))-1.0def mish(x):return x*tanh(softplus(x,20.0))20、hardmish激活函数
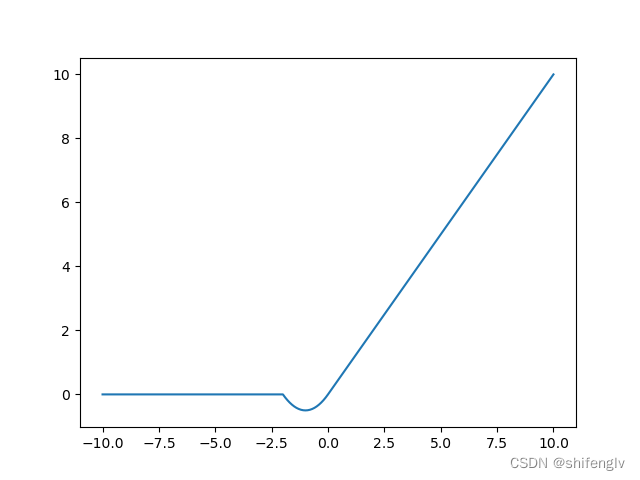
hardmish激活函数为mish激活函数的近似形式,它的图像如图20所示,其计算公式如下:
代码实现:
def hardmish(x):if x>0:return xelif x>-2:return x*x*0.5+xelse:return 0相关文章:

各种激活函数的计算公式、图像以及实现代码
激活函数已经成为神经网络中非常重要的一部分,随着各种类型的神经网络模型被人们开发出来,各种激活函数也应运而生,在不同的场景中,取得良好的效果。本文跟据著名的YOLO系列目标检测模型的源码 AlexeyAB Darknet,整理出…...

ArangoDB
介绍 ArangoDB 是一个原生的多模型开源数据库,具有灵活的文档、图形和键值数据模型。使用方便的类似 SQL 的查询语言或 JavaScript 扩展构建高性能应用程序。主要特点 在集群上安装 ArangoDB —— 安装简单灵活的数据建模:数据建模为键值对、文档或图表的…...

MySQL8.0Linux安装及主从的搭建
MySQL8.0Linux安装教程 下载并安装 需要说明的一点是我使用的是SSH secure shell Client连接linux系统的,它的用法和命令窗口差不多。界面如图:一样的使用Linux命令操作。 话不多说 第一步: 1)、切换到 /usr/local下 cd /usr/…...

苹果新专利实现无线技术传输睡眠数据,蓝牙在智能家居中的应用
苹果于 2017 年 5 月收购了芬兰科技公司 Beddit,只是在过去 6 年时间里并没有太大的动作。根据美国商标和专利局本周公示的清单,苹果获得了一项 Beddit 相关的技术专利。 根据专利描述,苹果使用一根或者多根天线,利用电磁辐射的…...
银行数字化转型导师坚鹏:数字化转型为什么需要致良知与知行合一
在银行数字化转型过程中,特别需要致良知与知行合一哲学思想的指导。 知中有行,行中有知;行极而知,知极而行;知行无端,知行无始。知与行是一件事,做事与培养本体(修心)也是…...
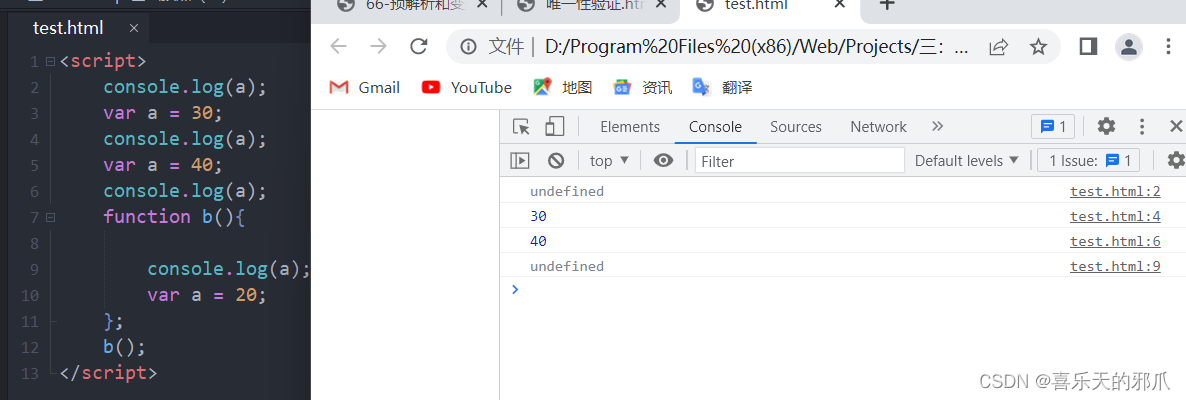
Web前端学习:章三 -- JavaScript预热(二)
六五:作用域与function function:函数,不是数学上的函数,与写代码有关 JS中的函数:运用它,起个名字,然后对函数进行调用,即可将函数中的内容执行一遍 1、function 最基本的作用域…...

Excel绘制数据对比表格-表格可视化
Word中生成的表格一般比较单调,若一组数据存在对比的情况时,读者/审稿人难以直接通过详细对比数据来分析,此时若可以将该组数据可视化来对比则为好,Excel则可实现该功能。 关于有些期刊需要提供表格中的数据便于复制等情况时&…...

究竟是谁负了谁,来自底层测试的2022年终总结
前言 说实话坐在椅子前,都想好了,该怎么去写,甚至感觉有好多要写的,但是当我坐在椅子上时,却不知道该怎么开头了,不知道是不是紧张?还是不舍?难道还没有跟过去挥手告别的勇气吗&…...
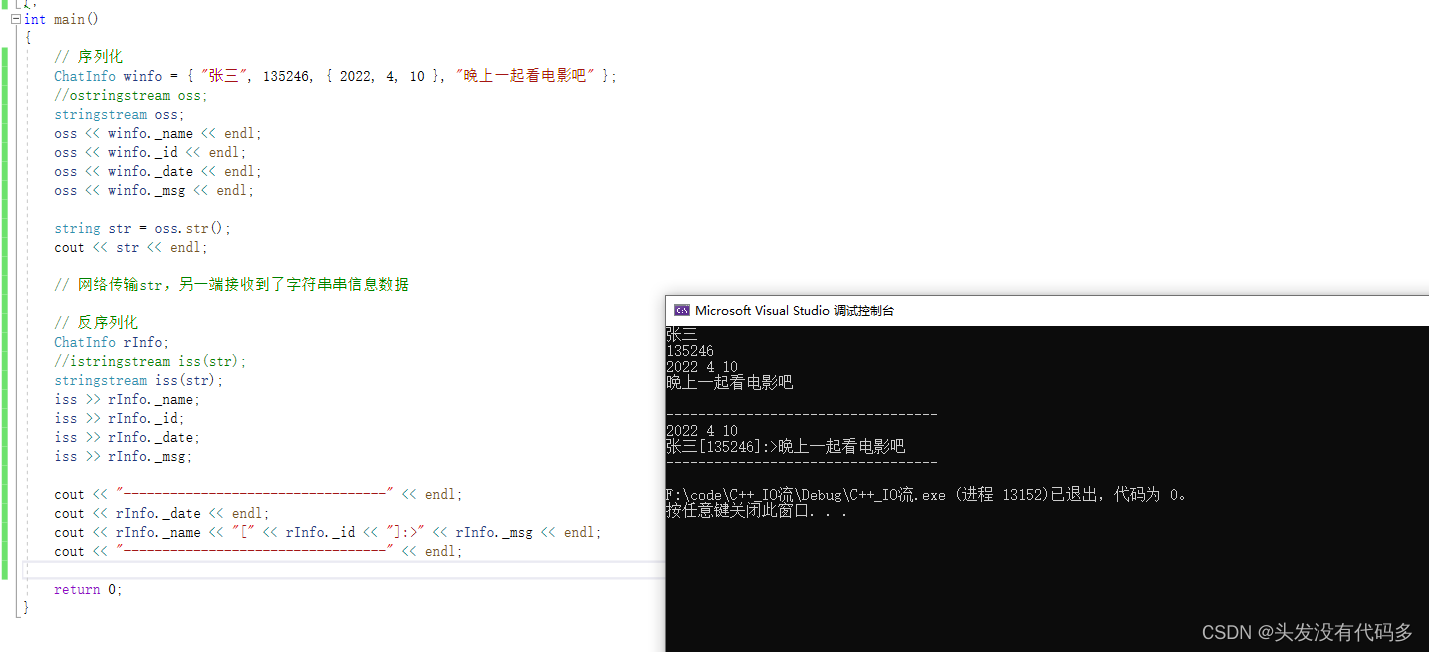
C++——IO流
目录 C语言的输入与输出 流是什么 CIO流 C标准IO流 C文件IO流 二进制读写 文本读写 stringstream的简单介绍 C语言的输入与输出 C语言中我们用到的最频繁的输入输出方式就是scanf ()与printf()。 scanf(): 从标准输入设备(键 盘)读取数据,并将值存放在变量中。…...

网络 | UDP与TCP协议讲解 | TCP可靠性是怎样实现的?
文章目录前置知识查看网络状态的工具查看进程idUDP协议协议格式UDP只有接收缓冲区基于UDP的应用层协议TCP协议流的理解协议格式确认应答机制缓冲区序号的作用流量控制超时重传机制6位标志位紧急数据的处理三次握手listen的第二个参数全连接和半连接队列都维护了什么信息&#x…...
JavaEE——简单介绍Thread类以及线程的基本操作
文章目录一、Thread 类中的常见构造方法二、Thread 的一些常见属性三、线程的启动——start()isAlive() 方法的解释四、线程中断五、线程等待-join()了解六、简单解释线程休眠一、Thread 类中的常见构造方法 我们已知,Thread 类是Java中多线程中的一个关键类&#…...

Java的数据库编程:JDBC
Content 🎉1什么是API 🎉2.什么是JDBC 🎉3.数据库驱动包的安装 🎉4.数据库安装包在idea的使用 🎉5.JDBC的增删改查的简单实现 今天为大家带来JAVA的数据库编程,也就是用Java实现数据库 数据库的最基本的操作就是…...

蓝桥冲刺31天之第六天
今天是摆子的一天,明天我要肝一整天的第四题!!! PS:一个普通的排序罢了 import java.io.*; import java.util.Arrays; import java.util.Scanner;/*** ClassName 考勤刷卡* Description TODO* Author 小怂很怂* Date 2…...

Streamlit 工具记录
Streamlit 是基于 Python 的 Web 应用程序框架,可视化数据,分析结果。 Streamlit 是一个开源库,可在短时间内开发机器学习可视化仪表板。只需几行代码就可以构部署强大的数据应用程序。Streamlit 可将仪表板的开发时间从几天缩短至几小时。 …...
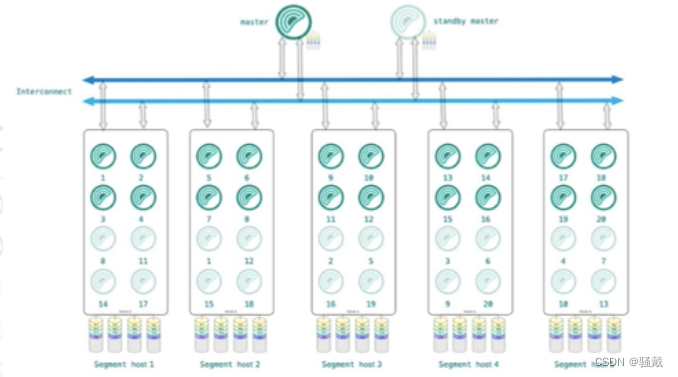
GreenPlum小结
什么是GreenPlum?GreenPlum是业界最快最高性价比的关系型分布式数据库,它在开源的PostgreSQL的基础上采用MPP架构(Massive Parallel Processing,海量并行处理),具有强大的大规模数据分析任务处理能力。GreenPlum作为大数据融合存储…...

C语言中数组和指针
文章目录前言一、指针的概念二、指针的大小三、指针的用法1.指针指向变量2.指针指向数组3.指针指向函数总结前言 本文将给大家带来C语言中非常重要的两个知识点,指针和数组。 一、指针的概念 指针,是C语言中的一个重要概念及其特点,也是掌…...
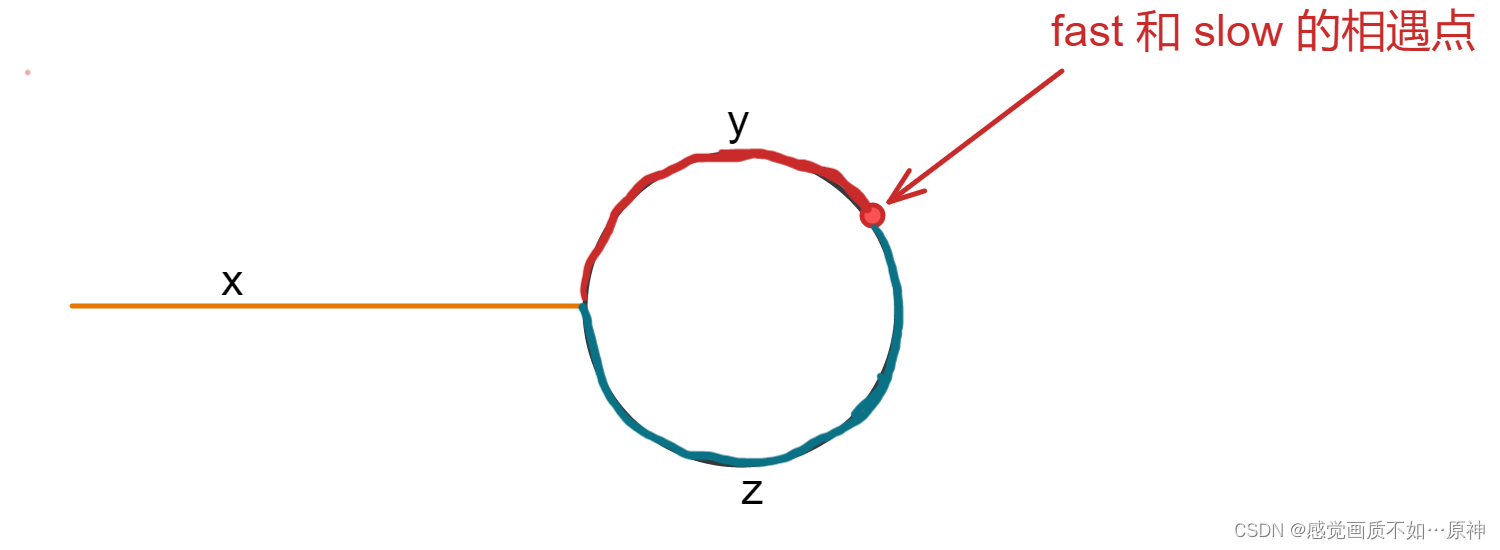
Leetcode.剑指 Offer II 022 链表中环的入口节点
题目链接 Leetcode.剑指 Offer II 022 链表中环的入口节点 mid 题目描述 给定一个链表,返回链表开始入环的第一个节点。 从链表的头节点开始沿着 next指针进入环的第一个节点为环的入口节点。如果链表无环,则返回 null。 为了表示给定链表中的环&#…...

4种不同编程语言的打印方式
意义 打印方式是编程中不可或缺的一部分,它可以帮助开发人员有效地调试和测试代码,并提供有用的信息来监视程序的运行状态和性能。 编程语言中的打印方式是指将程序输出到终端或控制台上进行显示。这个功能在编程中非常重要,因为它可以帮助开…...

websocket介绍
我们聊聊轮询技术,什么是轮询?轮询就是在特定的时间间隔,由浏览器对服务器发出HTTP请求,然后由服务器返回最新的数据给客户端的浏览器。 轮询分为两种: 短轮询:通过不断的向服务端发送数据,客户端发送Request,服务端直接返回Response(不管服务端数据有没有改变)。长轮…...
,C,D)
Educational Codeforces Round 144 (Rated for Div. 2),C,D
C. Maximum Set 思路: 我们求最大数组,显然是L一直乘2,直到再乘2就越过区间位置。我们说过,再乘一个2就不行,那么我们除一个2,换句话说,就是再乘一个4就不行了。发现,我们可能有机会乘一个3&a…...

超短脉冲激光自聚焦效应
前言与目录 强激光引起自聚焦效应机理 超短脉冲激光在脆性材料内部加工时引起的自聚焦效应,这是一种非线性光学现象,主要涉及光学克尔效应和材料的非线性光学特性。 自聚焦效应可以产生局部的强光场,对材料产生非线性响应,可能…...

基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容:参考网站: PID算法控制 PID即:Proportional(比例)、Integral(积分&…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

从“安全密码”到测试体系:Gitee Test 赋能关键领域软件质量保障
关键领域软件测试的"安全密码":Gitee Test如何破解行业痛点 在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的"神经中枢"。从国防军工到能源电力,从金融交易到交通管控,这些关乎国计民生的关键领域…...

基于stm32F10x 系列微控制器的智能电子琴(附完整项目源码、详细接线及讲解视频)
注:文章末尾网盘链接中自取成品使用演示视频、项目源码、项目文档 所用硬件:STM32F103C8T6、无源蜂鸣器、44矩阵键盘、flash存储模块、OLED显示屏、RGB三色灯、面包板、杜邦线、usb转ttl串口 stm32f103c8t6 面包板 …...
