C++实现的二叉树创建和遍历,超入门邻家小女也懂了

目录
二叉树
特点
性质
二叉树的创建
声明
创建
-> 成员运算符
批量创建
二叉树的遍历
先序遍历
中序遍历
后序遍历
层序遍历
树的相关术语
特殊二叉树
满二叉树
完全二叉树
二叉树
树(Tree)是n(n≥0)个节点的有限集。在任意一棵树中有且仅有一个特定的称为根(Root)的节点;当n>1时,其余节点可分m(m>0)为个互不相交的有限集T1,T2,...,Tm;其中每一个集合本身又是一棵树,并且称为根的子树(SubTree)。
二叉树(Binary Tree)是一种特殊的有序树型结构,所有节点最多只有2棵子树。
特点
(1)每个节点至多有两棵子树;
(2)二叉树的子树有左右之分;
(3)子树的次序不能任意颠倒(有序树)。
性质
(1)二叉树的第i层上至多有2^(i-1)个节点(i≥1)。
(2)深度为h的二叉树中至多含有2^h-1个节点(h≥1)。
(3)若在任意一棵二叉树中,有n0个叶子节点,有n2个度为2的节点,则必有n0=n2+1。
(4)具有n个节点的满二叉树深为log2n+1。
(5)若对一棵有n个节点的完全二叉树进行顺序编号(1≤i≤n),
那么,对于编号为i(i≥1)的节点:
当i=1时,该节点为根,它无双亲节点。
当i>1时,该节点的双亲节点的编号为i/2。
若2i≤n,则有编号为2i的左节点,否则没有左节点。
若2i+1≤n,则有编号为2i+1的右节点,否则没有右节点。
二叉树的创建
声明
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(NULL), right(NULL) {}
};在C/C++语言中,经常使用 NULL 来表示空指针。
NULL在头文件里的定义:
#ifndef NULL#ifdef __cplusplus#define NULL 0#else#define NULL ((void *)0)#endif
#endif即在 C++中,NULL 被定义为整形常量 0,而在 C 中,被定义为无类型指针常量 (void*) 0 。
C++11标准增加了新的关键字 nullptr,表示空指针。
建议使用C++11及以上版本的用以下的二叉树声明:
struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};创建
#include <iostream>struct TreeNode {int val;TreeNode* left;TreeNode* right;TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};int main() {TreeNode* root = new TreeNode(1);root->left = new TreeNode(2);root->right = new TreeNode(3);root->right->left = new TreeNode(4);root->right->right = new TreeNode(5);return 0;
}创建结果:
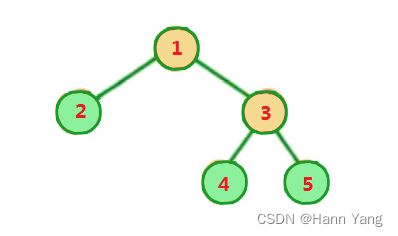
成员运算符->
指向结构体或对象的指针访问其内成员。当一个指针指向一个结构体、对象时,称之为结构体指针或对象指针。结构体指针或对象指针中的值是所指向的结构体或对象的首地址。通过结构体指针或对象指针即可访问该结构体或对象。
结构体指针变量定义的一般形式为:
struct 结构体类型名 *指针名; //结构体指针
struct 结构体类型名 *指针名 = &一个结构体的名字; //结构体指针并赋初值
struct 结构体类型名 *指针名 = new struct 结构体类型名; //结构体指针并用new申请内存
struct 结构体类型名 *指针名 =(struct 结构体类型名 *)malloc(sizeof(struct 结构体类型名))
//结构体指针并用malloc申请内存 使用应包含头文件stdlib.h子树root->left, root->right 还可以 . 运算表示,也成员运算符。两者的区别:
点运算符 . 左边必须用 * 寻址运算符取到指针root指向的结构或者对象实体,如(*root);对比箭头状的成员运算符 -> ,其左边必须为结构体指针,如root。
TreeNode* root = new TreeNode(1);(*root).left = new TreeNode(2);(*root).right = new TreeNode(3);(*(*root).right).left = new TreeNode(4);(*(*root).right).right = new TreeNode(5);批量创建
上例只是创建5节点,如要建更多节点,这样一个一个增加节点写起来复杂;可以用数组或容器等可迭代数据类型批量来创建。
代码明天补上
二叉树的遍历
指如何按某种搜索路径巡防树中的每个结点,使得每个结点均被访问一次,而且仅被访问一次。
常见的遍历方法有:先序遍历,中序遍历,后序遍历,层序遍历。
以一棵满二叉树为例:
_______1________/ \__2__ ___3___/ \ / \4 5 _6 _7/ \ / \ / \ / \
8 9 10 11 12 13 14 15先序遍历
若二叉树为空,为空操作;
否则(1)访问根节点;(2)先序遍历左子树;(3)先序遍历右子树。
遍历结果: 1 [2 [4 8 9] [5 10 11]] [3 [6 12 13] [7 14 15] “根左右”

中序遍历
若二叉树为空,为空操作;
否则(1)中序遍历左子树;(2)访问根结点;(3)中序遍历右子树。
遍历结果: [[8 4 9] 2 [10 5 11]] 1 [[12 6 13] 3 [14 7 15]] “左根右”

后序遍历
若二叉树为空,为空操作;
否则(1)后序遍历左子树;(2)后序遍历右子树;(3)访问根结点。
遍历结果: [[8 9 4] [10 11 5] 2] [[12 13 6] [14 15 7] 3] 1 “左右根”

层序遍历
若二叉树为空,为空操作;否则从上到下、从左到右按层次进行访问。
遍历结果: 1 [2 3] [4 5 6 7] [8 9 10 11 12 13 14 15]
代码明天补上
树的相关术语
节点:包含一个数据元素及若干指向其子树的分支,又的译成“结点”(Node)
根:树和子树的“顶点”(Root)
度:节点拥有的子树数量称为节点的度(Degree);树的度是指树内个结点的度的最大值
分支节点:度不为0的节点
叶子:没有子树的节点,即它的度为0 (Leaf)
子节点:结点的子树的根称为该节点的孩子(Child)
父节点:对应子节点上一层(level)节点称为该节点的双亲(Parent)
兄弟结点:同一父节点的子节点,互称兄弟(Sibling)
节点的祖先:是从根到该结点所经分支上的所有节点
节点的子孙:以某结点为根的子树中的所有节点
层:从根开始,根为第一层,根的孩子为第二层...(Level)
深度:树中结点的最大层次数,称为树的深度或高度 (Depth or Height)
森林:是很多互不相交的树的集合(Forest)
无序树:树中任意节点的子节点之间没有顺序关系,这种树称为无序树,也称为自由树
有序树:树中任意节点的子节点之间有顺序关系,这种树称为有序树
最大树(最小树):每个结点的值都大于(小于)或等于其子结点(如果有的话)值的树
特殊二叉树
满二叉树
所有层的节点都达到最大数量,叶子除外的所有节点都有两个子节点,所有叶子都在最底一层(k)且数目为2^(k - 1)。即深度k且有2^k - 1个节点(叶子“长”满最后一层),或称完美二叉树 (Perfect Binary Tree)
______12_______/ \__3__ __5__/ \ / \_7 6 _9 11/ \ / \ / \ / \
13 8 1 4 10 2 0 14完全二叉树
如果删除最底一层的所有叶子它就是满二叉树,即除了最后一层,每层节点都达到最大数量 ,即有深度k的个节点数在左闭右开【2^(k-1)+1,2^k-1】区间内。(Complete Binary Tree)
________3______/ \___11___ __4__/ \ / \14 7 9 13/ \ / \ /
2 5 8 6 1
完全二叉树性质:
1. 具有N个节点的完全二叉树的深度为[log2 N]+1,其中[x]为高斯函数,截尾取整。
2. 如果对一棵有n个节点的完全二叉树的节点按层序编号(从第一层到最后一层,每层从左到右),则对任一节点,有:
(1)如果i=1,则节点i是二叉树的根,无双亲;如果i>1,则其双亲节点为[i/2];
(2)如果2i>n,则节点i无左孩子;否则其左孩子是节点2i;
(3)如果2i+1>n,则节点i无右孩子;否则其右孩子是节点2i+1。
相关文章:

C++实现的二叉树创建和遍历,超入门邻家小女也懂了
目录 二叉树 特点 性质 二叉树的创建 声明 创建 -> 成员运算符 批量创建 二叉树的遍历 先序遍历 中序遍历 后序遍历 层序遍历 树的相关术语 特殊二叉树 满二叉树 完全二叉树 二叉树 树(Tree)是n(n≥0)个节点的有限集。在任意一棵…...

如何写出高质量的业务接口
清晰的需求 需求要有文档;方便后续追溯或交接等需求是基础,必须详细;多和需求沟通确认,不可模糊、模棱两可,否则后续可能越错越远 抽象建模 分析需求;梳理清楚关联关系,建立数据模型和关联画E-R…...

3.8多线程
案例一-线程安全的单例模式(面试)是一种设计模式,设计模式针对写代码时的一些常见场景给出一些经典解决方案单例模式的两种典型实现饿汉模式懒汉模式饿汉的单例模式:比较着急去进行创建实例懒汉的单例模式,是不太着急创建实例,,只是在用的时候,才真正创建这个是类对象,也就是.c…...
图文讲解MongoDB该怎么安装
一、安装前必读 我这里是Centos7 Linux 内核 注意:本文的命令使用的是 root 用户登录执行,不是 root 的话所有命令前面要加 sudo 二、环境配置 2.1 停止防火墙 systemctl status firewalld #查看firewall systemctl stop firewalld …...

「ML 实践篇」机器学习项目落地
文章目录1. 项目分析1. 框架问题2. 性能指标2. 获取数据1. 准备工作区2. 下载数据3. 查看数据4. 创建测试集3. 数据探索1. 地理位置可视化2. 寻找相关性3. 组合属性4. 数据准备1. 数据清理2. Scikit-Learn 的设计3. 处理文本、分类属性4. 自定义转换器5. 特征缩放6. 流水线5. 选…...

c++面试技巧-基础篇3
1.面试官:什么是函数的重载? 应聘者:函数的重载就是允许使用同一个函数名来定义多个函数,但是这些函数的参数个数和类型不同。 2.面试官:如何引用一个已经定义过的全局变量? 应聘者:可以用引…...

MySQL OCP888题解044-从服务器上导入mysql模式数据后的权限问题
文章目录1、原题1.1、英文原题1.2、中文翻译1.3、答案2、题目解析2.1、题干解析2.2、选项解析3、知识点3.1、知识点1:mysqldump的--flush-privileges选项3.2、知识点2:mysqldump的--all-databases选项3.3、知识点3:mysqldump默认不转储的内容…...
实战小项目之视频监控(1-2)
实战小项目之视频监控(1-2) Nginx 移植 前面也给大家提到了,我们可以使用 Nginx 来搭建 RTMP 流媒体服务器,譬如你可以在一台公网 IP 主 机上搭建流媒体服务器,当然,笔者并没有这个条件;这里我…...

人工智能基础--AI作业1-ML基础
1.监督学习和无监督学习都是机器学习中常用的方法。监督学习是一种机器学习方法,其中机器学习算法根据给定的输入数据和其对应的输出标签进行训练,以学习如何预测新的输入数据的输出标签。简单来说,监督学习就是通过已知的数据进行学习&#…...

关于JS中this对象指向问题总结
一、前言 关于JS中this对象指向问题,相信做过项目的小伙伴多多少少都会遇到过,明明感觉代码写的没问题,可是运行的时候,就会报错,比如报错 xxx is not a function。 我最近也遇到了,百度学习了不少前辈对于…...
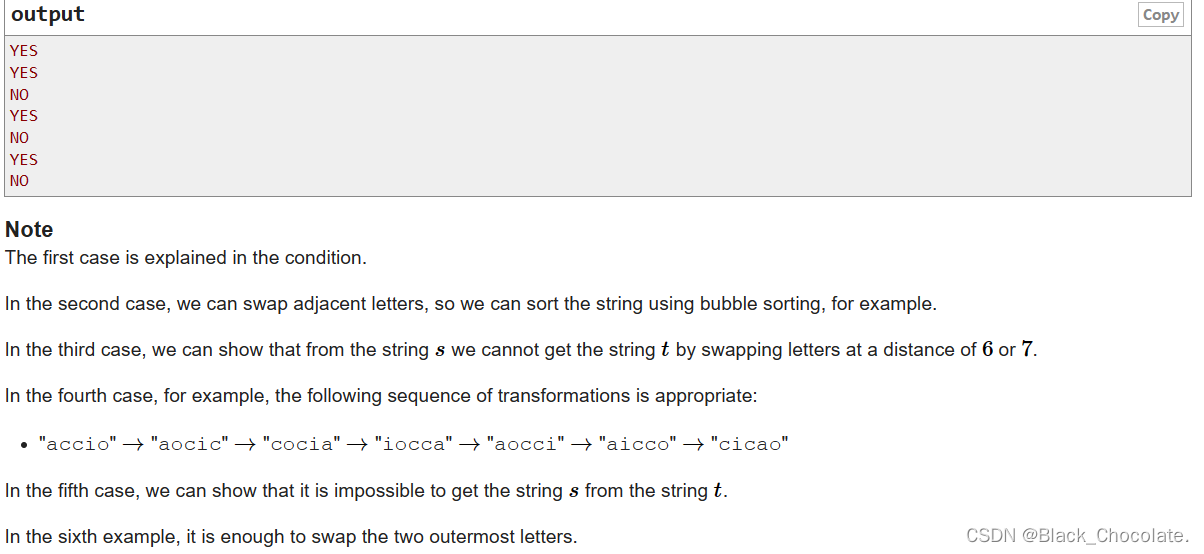
Codeforces Round 855 (Div. 3) A-E2
比赛链接:Dashboard - Codeforces Round 855 (Div. 3) - Codeforces A:模拟 题意:给定一个字符串,问这个字符串是不是猫叫。定义是猫叫得字符串: 1:必须由大写或小写得M(m),E&…...

Spark Yarn 运行环境搭建
文章目录Spark Yarn 运行环境搭建1、解压缩文件2、修改配置环境文件3、配置历史服务器Spark Yarn 运行环境搭建 1、解压缩文件 将spark3.2.3的压缩包上传到 linux /opt/software 目录下 输入命令: tar -zxvf spark-3.2.3-bin-hadoop3.2-scala2.13.tgz -C /opt/ 解…...

SpringMVC 页面跳转指南:转发和重定向的实现与比较
SpringMVC 是一款非常流行的 Java Web 框架,它提供了丰富的特性和功能,使得开发者可以轻松地开发 Web 应用程序。其中,转发和重定向是 SpringMVC 中非常常见的两个操作,它们可以用于控制请求的流转和页面的跳转。本文将深入探讨 S…...
ModStartCMS v5.9.0 后台浅色模式,系统样式升级
ModStart 是一个基于 Laravel 模块化极速开发框架。模块市场拥有丰富的功能应用,支持后台一键快速安装,让开发者能快的实现业务功能开发。 系统完全开源,基于 Apache 2.0 开源协议,免费且不限制商业使用。 功能特性 丰富的模块市…...

2020蓝桥杯真题反倍数 C语言/C++
题目描述 给定三个整数 a,b,c,如果一个整数既不是 a 的整数倍也不是 b 的整数倍还不是 c 的整数倍,则这个数称为反倍数。 请问在 1 至 n 中有多少个反倍数。 输入描述 输入的第一行包含一个整数 n。 第二行包含三个整数a,b,c,相邻两个数之…...

PTA:L1-025 正整数A+B、L1-026 I Love GPLT、L1-027 出租(C++)
目录 L1-025 正整数AB 问题描述: 实现代码: L1-026 I Love GPLT 问题描述: 实现代码: L1-027 出租 问题描述: 实现代码: 原理思路: 出租那道题有点意思哈 L1-025 正整数AB 问题描述…...
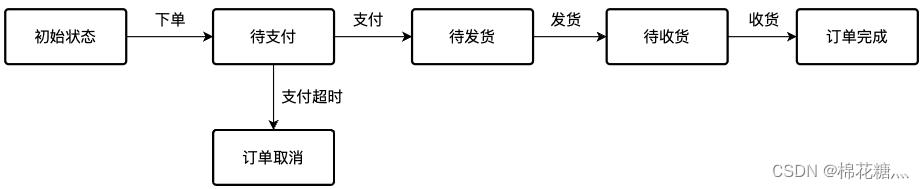
状态机的Go语言实现版本
一、状态机 1. 定义 有限状态机(Finite-state machine, FSM),简称状态机,是表示有限个状态以及在这些状态之间的转移和动作等行为的数学模型。 2. 组成要素 现态(src state):事务当前所处的状…...

第2章 线程安全与共享资源竞争
第2章 线程安全与共享资源竞争 2.1 synchronized同步介绍 synchronized要解决的是共享资源冲突的问题。当共享资源被任务使用时,要对资源提前加锁。所有任务都采用抢占模式,即某个任务会抢先对共享资源加上第一把锁。如果这是一个排他锁,…...

77. writerows写入多行
文章目录1. 目标任务2. 准备工作3. writerow单行写入4. writerows多行写入5. a以追加的模式写入值6. 总结1. 目标任务 新建【各班级成绩】文件夹; 在该文件夹下新建一个【1班成绩单.csv】文件; 在该文件中写入下面的内容: 成绩 姓名 刘一…...

STM32MP157-Linux输入设备应用编程-多点触摸屏编程
文章目录前言多点触摸屏tslib库简介tslib库移植tslib库函数使用打开触摸屏设备配置触摸屏设备打开并配置触摸屏设备读取触摸屏设备多点触摸屏程序编写触点数据结构体定义事件定义计算触点数量判断单击、双击判断长按、移动判断放大、缩小外部调用代码流程图(草图&am…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

1.3 VSCode安装与环境配置
进入网址Visual Studio Code - Code Editing. Redefined下载.deb文件,然后打开终端,进入下载文件夹,键入命令 sudo dpkg -i code_1.100.3-1748872405_amd64.deb 在终端键入命令code即启动vscode 需要安装插件列表 1.Chinese简化 2.ros …...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...
