【洛谷 P1443】马的遍历 题解(广度优先搜索)
马的遍历
题目描述
有一个 n×mn \times mn×m 的棋盘,在某个点 (x,y)(x, y)(x,y) 上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步。
输入格式
输入只有一行四个整数,分别为 n,m,x,yn, m, x, yn,m,x,y。
输出格式
一个 n×mn \times mn×m 的矩阵,代表马到达某个点最少要走几步(不能到达则输出 −1-1−1)。
样例 #1
样例输入 #1
3 3 1 1
样例输出 #1
0 3 2
3 -1 1
2 1 4
提示
数据规模与约定
对于全部的测试点,保证 1≤x≤n≤4001 \leq x \leq n \leq 4001≤x≤n≤400,1≤y≤m≤4001 \leq y \leq m \leq 4001≤y≤m≤400。
思路
- 马走“日”
- 输出格式:域宽为5,左对齐
- 注意判断是否越界
AC代码
#include <iostream>
#include <queue>
#include <cstring>
#define AUTHOR "HEX9CF"
using namespace std;const int maxn = 405;
const int sun[8][2] = {-2, 1, -2, -1, -1, 2, -1, -2, 2, 1, 2, -1, 1, 2, 1, -2};
int n, m, x, y;bool vis[maxn][maxn];
int stp[maxn][maxn];
queue<pair<int, int>> q;void bfs(int x, int y)
{vis[x][y] = 1;stp[x][y] = 0;q.push(make_pair(x, y));while (!q.empty()){pair<int, int> f = q.front();q.pop();for (int i = 0; i < 8; i++){int xx = f.first + sun[i][0];int yy = f.second + sun[i][1];if (xx > 0 && xx <= n && yy > 0 && yy <= m && !vis[xx][yy]){vis[xx][yy] = 1;q.push(make_pair(xx, yy));stp[xx][yy] = stp[f.first][f.second] + 1;}}}
}int main()
{memset(vis, 0, sizeof(vis));memset(stp, -1, sizeof(stp));cin >> n >> m >> x >> y;stp[x][y] = 0;vis[x][y] = true;q.push(make_pair(x, y));bfs(x, y);for (int i = 1; i <= n; i++){for (int j = 1; j <= m; j++){printf("%-5d", stp[i][j]);}putchar('\n');}return 0;
}
相关文章:
)
【洛谷 P1443】马的遍历 题解(广度优先搜索)
马的遍历 题目描述 有一个 nmn \times mnm 的棋盘,在某个点 (x,y)(x, y)(x,y) 上有一个马,要求你计算出马到达棋盘上任意一个点最少要走几步。 输入格式 输入只有一行四个整数,分别为 n,m,x,yn, m, x, yn,m,x,y。 输出格式 一个 nmn \t…...

为什么gpt输出有随机性?
以下答案由chatGPT产生! 为什么gpt输出有随机性? GPT(Generative Pre-trained Transformer)是一种基于Transformer架构的神经语言模型,它是一个深度学习模型,通过在大规模文本数据上进行预训练࿰…...
配置Clion用于STM23开发(Makefile)
前言 对于Clion配置STM32开发环境的教程在网上一搜一大堆,但是大部分都是22年之前的,使用的方法都是在STM32CubeMX生成SW4STM32工程。但是在22年不知道哪个版本后,CubeMX已经不再支持生成SW4STM32工程了,这也是我本人遇到的问题。…...

如何在 Istio 中使用 SkyWalking 进行分布式追踪
在云原生应用中,一次请求往往需要经过一系列的 API 或后台服务处理才能完成,这些服务有些是并行的,有些是串行的,而且位于不同的平台或节点。那么如何确定一次调用的经过的服务路径和节点以帮助我们进行问题排查?这时候…...

HBase高手之路1-Hbase简介
文章目录HBase高手之路1-Hbase简介一、什么是HBase1. HBase简介2. HBase的发展过程二、HBase特点1. 海量存储2. 列式存储3. 极易扩展4. 高并发5. 稀疏6. 强一致性读/写7. 自动分块8. 自动RegionServer故障转移9. Hadoop/HDFS集成10. MapReduce11. Java Client API12. Thrift/RE…...

计算机视觉手指甲标注案例
关键点标注是指识别和标注图像或视频中特定的相关点或区域的过程。在机器学习行业,它经常被用来训练计算机视觉模型,以执行诸如物体检测、分割和跟踪等任务。 关键点注释可用于以下应用: 面部关键点检测:识别图像中人脸上的眼睛…...
)
linux 字符串截取(cut)
-b :以字节为单位进行分割。这些字节位置将忽略多字节字符边界,除非也指定了 -n 标志。 -c :以字符为单位进行分割。 -d :自定义分隔符,默认为制表符。 -f :与-d一起使用,指定显示哪个区域。 -n…...

003+limou+HTML——(3)HTML列表
000、前言 列表是网页常见的一种数据排列方式,在HTMl中列表一共有三种:有序列表、无序列表、定义列表(另外“目录列表dir”和“菜单列表menu”已经在HTML5中被废除了,现在都是使用无序列表ul来替代) 001、有序列表&a…...

设计模式---工厂模式
目录 1. 简单工厂模式 2. 工厂方法模式 1. 简单工厂模式 简单工厂模式(Simple Factory Patterm)又称为静态工厂方法模式(Static Factory Model),它属于类创建型模式。在简单工厂模式中,可以根据参数的不同返回不同类的实例。简单工厂模式专门定义了一…...

C++基础了解-13-C++ 数组
C 数组 一、C 数组 C 支持数组数据结构,它可以存储一个固定大小的相同类型元素的顺序集合。数组是用来存储一系列数据,但它往往被认为是一系列相同类型的变量。 数组的声明并不是声明一个个单独的变量,比如 number0、number1、…、number9…...

ICC2:限制LVT比例
1) 禁用VT 在优化过程用,如果要禁用某种VT可以直接对其使用dont use,如下示例: set_attribute -objects [get_lib_cells *_lvt*/*] -name dont_use -value true 在dont use lib cell的基础上还可以对某些模块放开lvt的使用。 set_app_options -name …...
Kettle工具通过JNDI连接Oracle集群
我们在用Kettle ETL工具的时候,可能会遇到数据库为Oracle集群的模式,或者有时候目标库为oracle,在持续的循环调度中,经常发现oracle的数据库连接中断的情况,此时,在Kettle中有一个JNDI的连接方式能很好的解…...

[ 常用工具篇 ] windows安装phpStudy_v8.1_X64
🍬 博主介绍 👨🎓 博主介绍:大家好,我是 _PowerShell ,很高兴认识大家~ ✨主攻领域:【渗透领域】【数据通信】 【通讯安全】 【web安全】【面试分析】 🎉点赞➕评论➕收藏 养成习…...

SpringBoot 如何将配置文件挂到 jar 包外面?
目录一、SpringBoot 指定配置文件路径:1)使用命令行参数:2)使用环境变量:3)使用外部配置文件:二、SpringBoot 配置文件生效的优先级排序:一、SpringBoot 指定配置文件路径࿱…...

蓝桥杯C/C++b组第一题个人整理合集(5年真题+模拟题)
蓝桥杯C/Cb组填空第一题合集 前言 比赛标准的签到题,比赛时的第一题。不会考到什么算法,甚至都不需要你打代码。但有时候第一题都没做出来的确是非常挫灭信心 看了看历年题目。很多小陷阱也不少 今年的比赛也正好还有一个月,自己对填空题第…...

深入浅出PaddlePaddle函数——paddle.zeros
分类目录:《深入浅出PaddlePaddle函数》总目录 相关文章: 深入浅出PaddlePaddle函数——paddle.Tensor 深入浅出PaddlePaddle函数——paddle.ones 深入浅出PaddlePaddle函数——paddle.zeros 深入浅出PaddlePaddle函数——paddle.full 深入浅出Padd…...

[力扣sql]
题目 表: Person ---------------------- | 列名 | 类型 | ---------------------- | PersonId | int | | FirstName | varchar | | LastName | varchar | ---------------------- personId 是该表的主键列。 该表包含一些人的 ID 和他们的姓和名的信…...
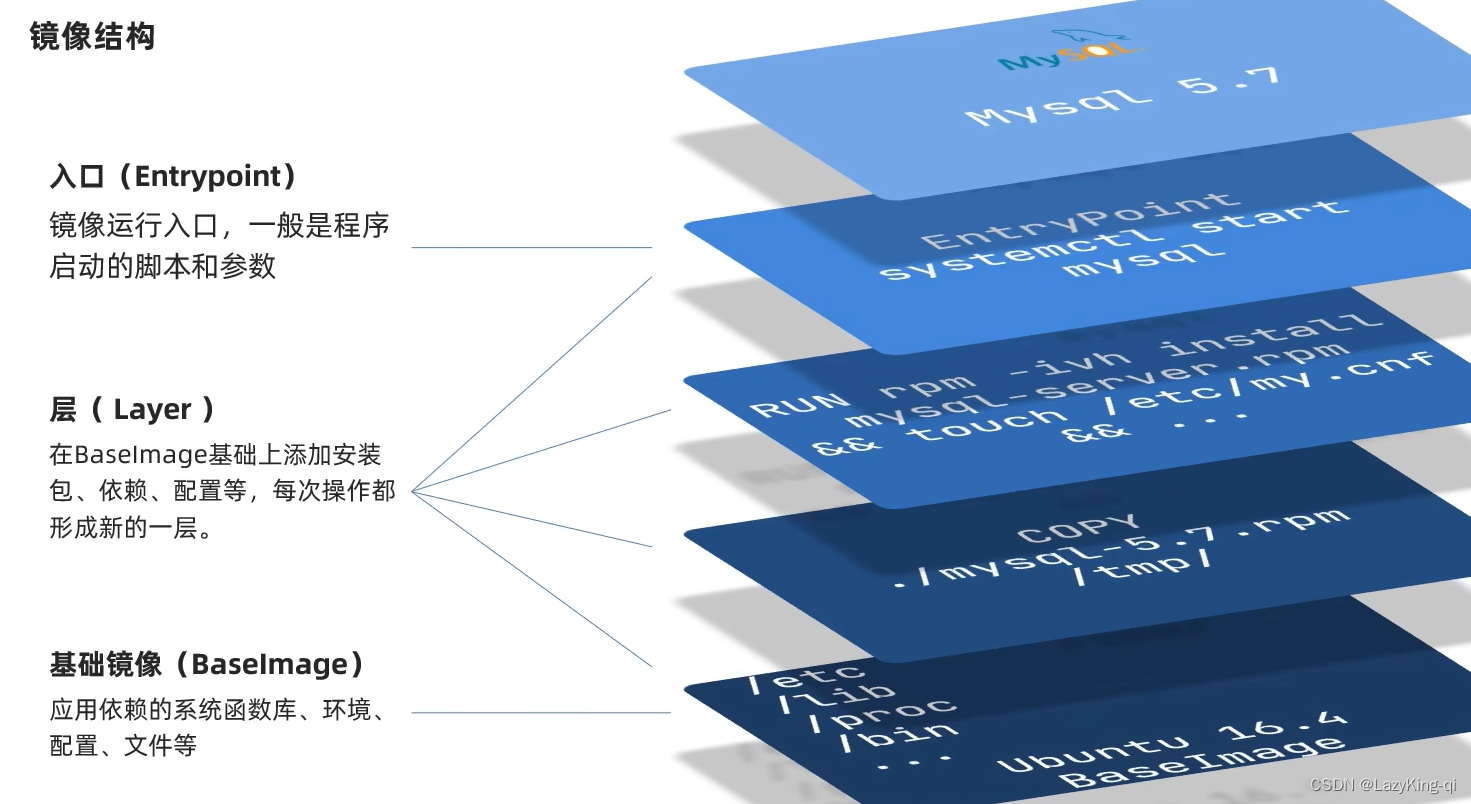
Docker基本操作
目录 Docker基本操作 1、镜像操作 2、容器操作 3、数据卷(容器数据管理) 4、数据卷挂载 5、Dockerfile自定义镜像 Docker基本操作 1、镜像操作 镜像名称一般分两部分组成:[repository]:[tag]。 在没有指定tag时,默认是la…...

golang如何使用rocketmq 附加闭坑指南 建议收藏!!!
文章目录前言一、rocketmq是什么?二、rocketmq核心概念三、rocketmq核心应用四、go如何使用rocketmq总结前言 当我们的业务达到一定规模,很多业务需要解耦,以及需要流量削峰的时候,我们需要使用MQ来让我们系统能够正常运转。 一…...

C++实现的二叉树创建和遍历,超入门邻家小女也懂了
目录 二叉树 特点 性质 二叉树的创建 声明 创建 -> 成员运算符 批量创建 二叉树的遍历 先序遍历 中序遍历 后序遍历 层序遍历 树的相关术语 特殊二叉树 满二叉树 完全二叉树 二叉树 树(Tree)是n(n≥0)个节点的有限集。在任意一棵…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

质量体系的重要
质量体系是为确保产品、服务或过程质量满足规定要求,由相互关联的要素构成的有机整体。其核心内容可归纳为以下五个方面: 🏛️ 一、组织架构与职责 质量体系明确组织内各部门、岗位的职责与权限,形成层级清晰的管理网络…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

Swagger和OpenApi的前世今生
Swagger与OpenAPI的关系演进是API标准化进程中的重要篇章,二者共同塑造了现代RESTful API的开发范式。 本期就扒一扒其技术演进的关键节点与核心逻辑: 🔄 一、起源与初创期:Swagger的诞生(2010-2014) 核心…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

嵌入式学习之系统编程(九)OSI模型、TCP/IP模型、UDP协议网络相关编程(6.3)
目录 一、网络编程--OSI模型 二、网络编程--TCP/IP模型 三、网络接口 四、UDP网络相关编程及主要函数 编辑编辑 UDP的特征 socke函数 bind函数 recvfrom函数(接收函数) sendto函数(发送函数) 五、网络编程之 UDP 用…...
