每日一练-等差数列
等差数列
- 🍀题目描述
- 🌿解题思路
- 🌸Python源码
- 📧Summary
📆Date: 2023年2月10日
🎬Author: 小 y 同 学
📃Classify: 蓝桥杯每日一练
🔖Language: Python
🍀题目描述
题意
数学老师给小明出了一道等差数列求和的题目。但是粗心的小明忘记了一部分的数列,只记得其中 N 个整数。
现在给出这 N 个整数,小明想知道包含这 N 个整数的最短的等差数列有几项?输入格式
输入的第一行包含一个整数 N。
第二行包含 N 个整数 A1, A2, · · · , AN。(注意 A1 ∼ AN 并不一定是按等差数列中的顺序给出)输出格式
输出一个整数表示答案。样例输入
5 2 6 4 10 20
- 样例输出
10
样例说明
包含 2、6、4、10、20 的最短的等差数列是 2、4、6、8、10、12、14、16、18、20。评测用例规模与约定
对于所有评测用例,2 ≤ N ≤ 100000,0 ≤ Ai ≤ 109。
🌿解题思路
- 题目梳理
题目会给出一串数字,我们需要做的就是找出包含这些数字的等差数列,且这个等差数列的项数最小,注意我们要输出的是等差数列的项数,不是等差数列的元素或者其求和。- 核心处理
首先给出的数字串是没有顺序的,我们首先肯定是想到将给出的数字排序。然后我们要做的就是寻找公差:起初小y想的是排序完的数组每相邻两项做差,然后最小的就是公差,但是仔细一想:如果排序完的数组中的相邻两项差一个是2,一个是3:例如数组:1、3、6;要想组成等差数列,必须以1为公差;随后就想到了取2和3的最大公因数也就是1来作为公差;同样的思路,就可以类比出给出的任意数列对应的公差。随后就是求项数,给出的数列最小的和最大的一定是等差数列的首尾项,我们可以由an=a1+(n−1)×da_n=a_1+(n-1)\times dan=a1+(n−1)×d推导出n=an−a1d+1n=\frac{a_n - a_1}{d}+1n=dan−a1+1,但是我们要注意d为0的情况分开讨论!
🌸Python源码
# _*_coding:utf-8_*_ # created by cy on 2023/2/10 import math# 求最大公因数 def gcd_many(li, n): g = 0 for i in range(n):if i == 0:g = li[i]else:g = math.gcd(g, li[i]) return gn = int(input()) A = list(map(int, input().split())) A.sort() d_li = [] for i in range(n - 1): d_li.append(A[i + 1] - A[i]) if min(d_li) == 0: # 公差为0的情况 print(n) else: d = gcd_many(A, n) print(int((A[-1] - A[0]) / d + 1))
📧Summary
小y的今日一练到此画上了句号,欢迎友友们多给建议🌼🌼🌼
有兴趣一起学习编程的小伙伴可以私聊小y一起学习,小y在Python,c/c++和matlab语言上均有一定的基础😜😜😜
相关文章:

每日一练-等差数列
等差数列🍀题目描述🌿解题思路🌸Python源码📧Summary📆Date: 2023年2月10日 🎬Author: 小 y 同 学 📃Classify: 蓝桥杯每日一练 🔖Language: Python 🍀题目描述 题意 …...
使用动态参数构建CUDA图
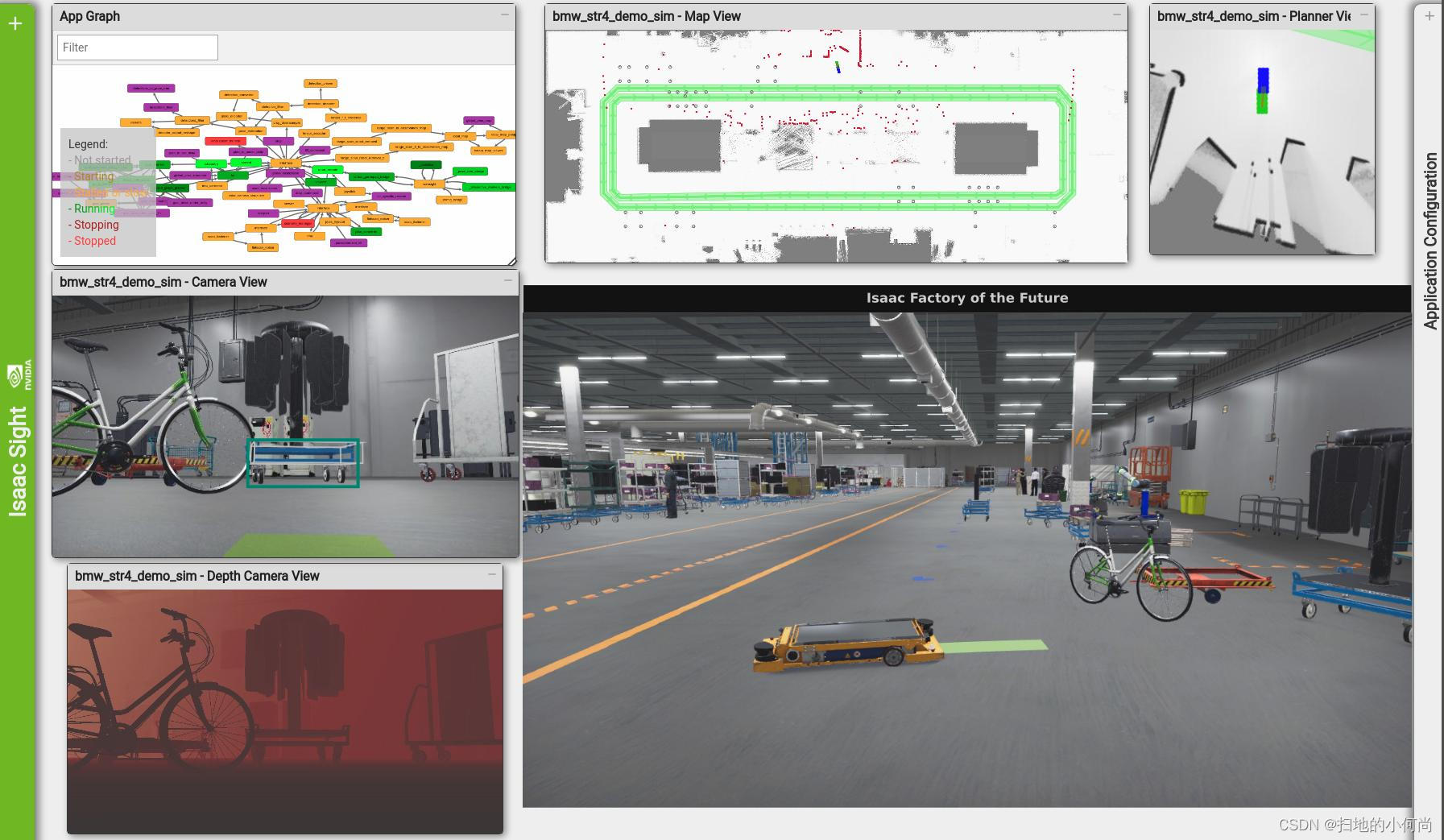
文章目录使用动态参数构建CUDA图使用显式 API 调用构建 CUDA 图使用流捕获构建 CUDA 图组合方法执行结果总结使用动态参数构建CUDA图 自从在 CUDA 10 以来,CUDA Graphs 已被用于各种应用程序。 上图将一组 CUDA 内核和其他 CUDA 操作组合在一起,并使用指…...

在Fortran中调用Python教程
前言Python是机器学习领域不断增长的通用语言。拥有一些非常棒的工具包,比如scikit-learn,tensorflow和pytorch。气候模式通常是使用Fortran实现的。那么我们应该将基于Python的机器学习迁移到Fortran模型中吗?数据科学领域可能会利用HTTP AP…...
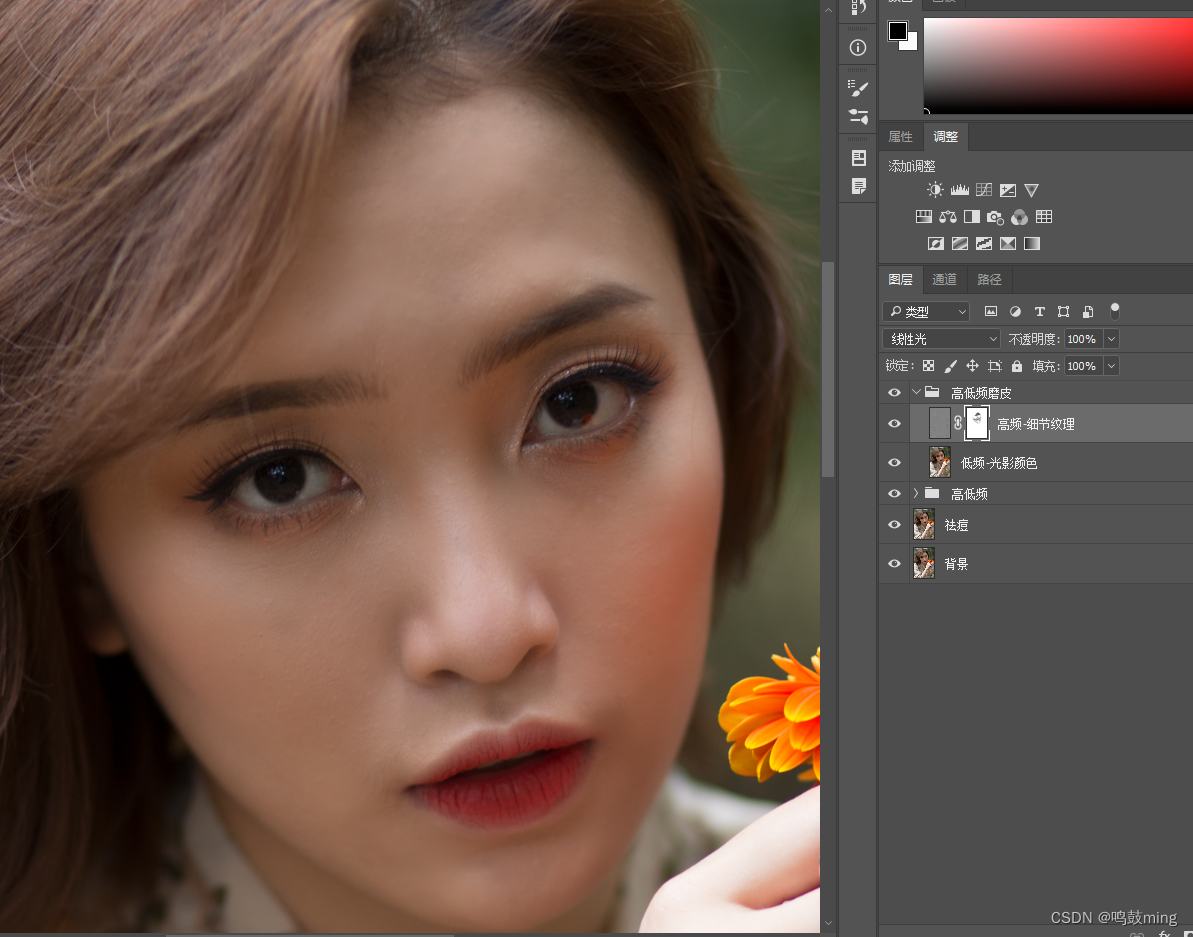
04-PS人像磨皮方法
1.高斯模糊磨皮 这种方法的原理就是建立一个将原图高斯模糊后图层, 然后用蒙版加画笔或者历史画笔工具将需要磨皮的地方涂抹出来, 通过图层透明度, 画笔流量等参数来控制磨皮程度 1.新建图层(命名为了高斯模糊磨皮), 混合模式设置为正常, 然后选择高斯模糊, 模糊数值设置到看…...
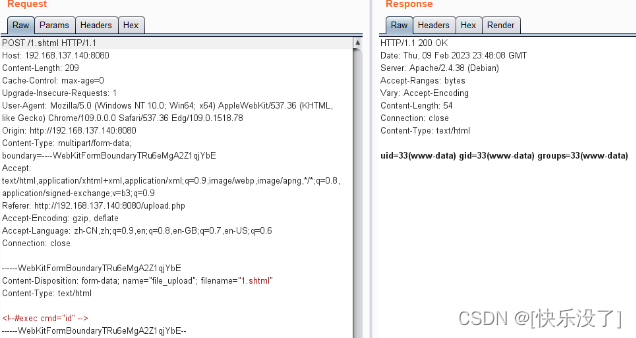
nginx反向代理+负载均衡上传webshell重难点+apache漏洞
nginx反向代理 nginx 负载均衡 负载均衡的策略 1、轮询:nginx默认就是轮询其权重都默认为1,服务器处理请求的顺序:ABABABABAB… upstream mysvr { server 192.168.137.131; server 192.168.137.136; }2、weight:跟据配置…...

transition组件的使用
<template><button click"flag !flag">切换</button><transition name"fade"><div v-if"flag" class"box"></div></transition> </template><script setup lang"ts"&g…...
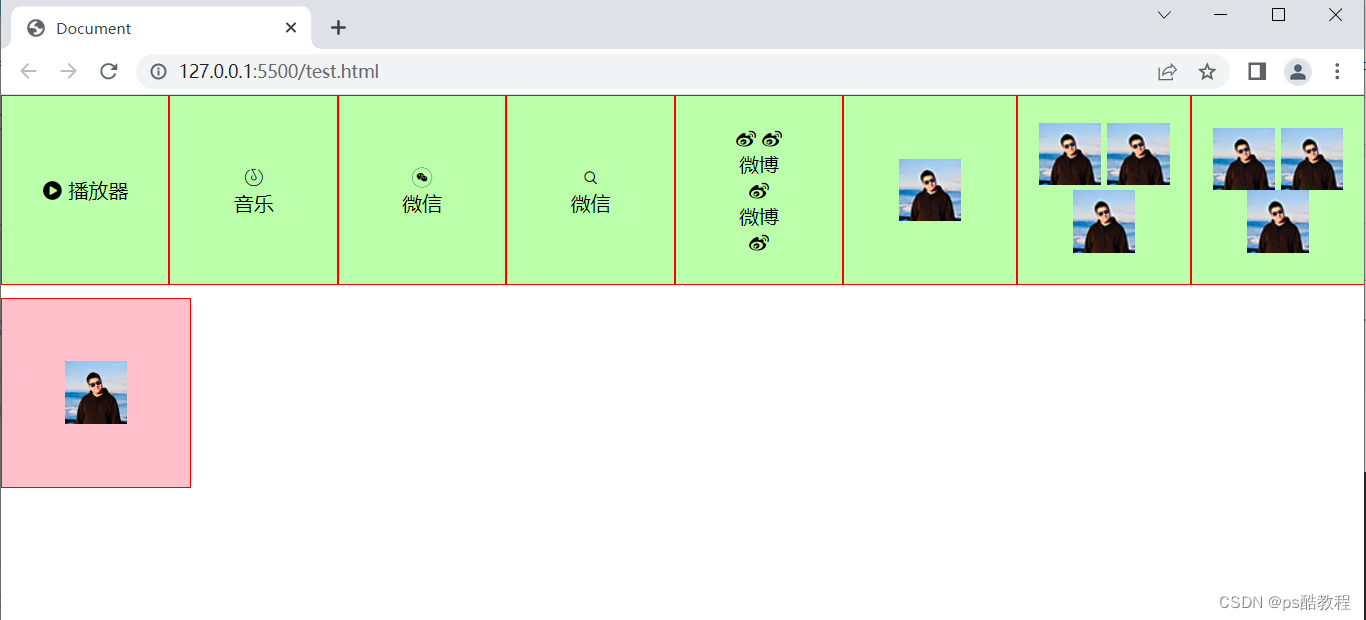
多行文本在块元素中垂直居中
单行文本垂直居中对齐 在块元素中,让单行文本居中,可以使用line-height等于块元素的高,即可让该单行文本垂直居中对齐。 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><me…...

在 WebAssembly 中使用 C/C++ 和 libbpf 编写 eBPF 程序
作者:于桐,郑昱笙 eBPF(extended Berkeley Packet Filter)是一种高性能的内核虚拟机,可以运行在内核空间中,用来收集系统和网络信息。随着计算机技术的不断发展,eBPF 的功能日益强大,…...

leveldb源码解析六——compact
compact分为manual_compaction、minor_compaction、major_compaction,统一由MaybeScheduleCompaction触发: void DBImpl::MaybeScheduleCompaction() {mutex_.AssertHeld();if (background_compaction_scheduled_) {// Already scheduled} else if (shu…...

数据结构(二):单向链表、双向链表
数据结构(二)一、什么是链表1.数组的缺点2.链表的优点3.链表的缺点4.链表和数组的区别二、封装单向链表1. append方法:向尾部插入节点2. toString方法:链表元素转字符串3. insert方法:在任意位置插入数据4.get获取某个…...

COCO物体检测评测方法简介
本文从ap计算到map计算,最后到coco[0.5:0.95:0.05] map的计算,一步一步拆解物体检测指标map的计算方式。 一、ap计算方法 一个数据集有多个类别,对于该数据库有5个gt,算法检测出来10个bbox,对于人这个类别来说检测有…...

记一次上环境获取资源失败的案例
代码结构以及资源位置 测试代码 RestController RequestMapping("/json") public class JsonController {GetMapping("/user/1")public String queryUserInfo() throws Exception {// 如果使用全路径, 必须使用/开头String path JsonController.class.ge…...

实战超详细MySQL8离线安装
在RedHat中,RPM Bundle 方式安装MySQL8。建议一定要用 RPM Bndle 版本安装,包全。官网下载:https://dev.mysql.com/downloads/mysql/1.卸载mariadb,会与MySQL安装冲突。rpm -qa | grep mariadb 查看有无mariadb如果有࿰…...

依赖倒置原则|SOLID as a rock
文章目录 意图动机:违反依赖倒置原则解决方案:C++中依赖倒置原则的例子依赖倒置原则的优点1、可复用性2、可维护性在C++中用好DIP的标准总结本文是关于 SOLID as Rock 设计原则系列的五部分中的 最后一部分。 SOLID 设计原则侧重于开发 易于维护、可重用和可扩展的软件。 在…...
Webpack的知识要点
在前端开发中,一般情况下都使用 npm 和 webpack。 npm是一个非常流行的包管理工具,帮助开发者管理项目中使用的依赖库和工具。它可以方便地为项目安装第三方库,并在项目开发过程中进行版本控制。 webpack是一个模块打包工具ÿ…...
handler解析(2) -Handler源码解析
目录 基础了解: 相关概念解释 整体流程图: 源码解析 Looper 总结: sendMessage 总结: ThreadLocal 基础了解: Handler是一套 Android 消息传递机制,主要用于线程间通信。实际上handler其实就是主线程在起了一…...

【算法】kmp
KMP算法 名称由来 是由发明这个算法的三个科学家的名称首字母组成 作用 用于字符串的匹配问题 举例说明 字符串 aabaabaaf 模式串 aabaaf 传统匹配方法 第一步 aabaabaaf aabaaf 此时,b和f不一致,则把模式串从头和文本串的第二个字符开始比 第…...
git 常用命令之 git checkout
大家好,我是 17。 git checkout 是 git 中最重要最常用的命令之一,本文为大家详细解说一下。 恢复工作区 checkout 的用途之一是恢复工作区。 git checkout . checkout . 表示恢复工作区的所有更改,未跟踪的文件不会有变化。 恢复工作区的所有文件风…...
一些常见错误
500状态码: 代表服务器业务代码出错, 也就是执行controller里面的某个方法的过程中报错, 此时在IDEA的控制台中会显示具体的错误信息, 所以需要去看IDEA控制台的报错404状态码: 找不到资源找不到静态资源 检查请求地址是否拼写错误 检查静态资源的位置是否正确 如果以上都没有问…...
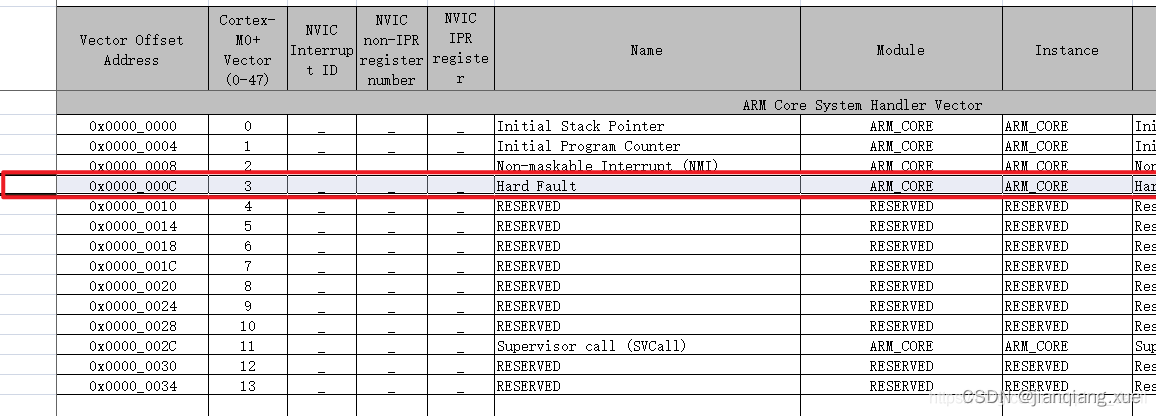
[单片机框架][调试功能] 回溯案发现场
程序莫名死机跑飞,不知道问题,那么下面教你回溯错误源 回溯案发现场一、修改HardFault_Handler1. xx.s 在启动文件,找到HardFault_Handler。并修改。2. 定义HardFault_Handler_C函数。(主要是打印信息并存储Flash)3. 根…...
)
uniapp 对接腾讯云IM群组成员管理(增删改查)
UniApp 实战:腾讯云IM群组成员管理(增删改查) 一、前言 在社交类App开发中,群组成员管理是核心功能之一。本文将基于UniApp框架,结合腾讯云IM SDK,详细讲解如何实现群组成员的增删改查全流程。 权限校验…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...
