数据结构刷题(二十):17电话号码的字母组合、39组合总和、40组合总和II
一、电话号码的字母组合
题目链接
思路:回溯三部曲。
确定回溯函数参数:题目中给的 digits,还要有一个参数就是int型的index(记录遍历第几个数字,就是用来遍历digits的,同时也代表了递归的深度),第三个参数numString(数字和字母映射)。
确定终止条件:如果index 等于 输入的数字个数(digits.size)了,就return。
确定单层遍历逻辑:首先要取index指向的数字,并找到对应的字符集;然后for循环来处理这个字符集
注意:
(1)解决三个问题
数字和字母如何映射 (使用map或者定义一个二维数组)
两个字母就两个for循环,三个字符我就三个for循环,以此类推,然后发现代码根本写不出来
输入1 * #按键等等异常情况
(2)区别于普通的组合问题,本题是多个集合求组合,因为本题每一个数字代表的是不同集合,也就是求不同集合之间的组合。
(3)全局变量:一个字符串sb来收集叶子节点的结果,一个字符串数组result保存sb。
解法:
class Solution {// 最终结果字符数组和单次符合条件结果List<String> res = new ArrayList<>();StringBuffer sb = new StringBuffer();public List<String> letterCombinations(String digits) {if (digits.length() == 0 || digits == null)return res;String[] numString = {"", "", "abc", "def", "ghi", "jkl", "mno", "pqrs", "tuv", "wxyz"};backTracking(digits, numString, 0);return res;}public void backTracking(String digits, String[] numString ,int num) {if (num == digits.length()){res.add(sb.toString());return;}// digits.charAt(num)能够获取到当前的号码数字,2-9String t = numString[digits.charAt(num) - '0'];for (int i = 0; i < t.length(); i++) {sb.append(t.charAt(i));backTracking(digits, numString, num + 1);sb.deleteCharAt(sb.length() - 1); //回溯}}
}二、组合总和
题目链接
思路:基本与组合总和III类似。区别有:
组合没有数量要求
元素可无限重复选取
注意:
如果是一个集合来求组合的话,就需要startIndex;(否则会出现重复情况)
如果是多个集合取组合,各个集合之间相互不影响,那么就不用startIndex。
解法(未剪枝):
List<List<Integer>> res = new ArrayList<>();
LinkedList<Integer> path = new LinkedList<>();
public List<List<Integer>> combinationSum(int[] candidates, int target) {// sum, startIndex是开始位置也是candidates的索引back(candidates, target, 0,0);return res;
}private void back(int[] candidates, int target, int sum, int startIndex) {if (sum == target){res.add(new ArrayList<>(path));return;}if (sum > target)return;for (int i = startIndex; i < candidates.length; i++){path.add(candidates[i]);sum += candidates[i];back(candidates, target, sum, i);sum -= candidates[i];path.removeLast();}
}剪枝优化:
1.对总集合排序之后,如果下一层的sum(就是本层的 sum + candidates[i])已经大于target,就可以结束本轮for循环的遍历。
解法:
class Solution {List<List<Integer>> res = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combinationSum(int[] candidates, int target) {Arrays.sort(candidates); // 先进行排序back(candidates, target, 0, 0);return res;}private void back(int[] candidates, int target, int sum, int startIndex) {if (sum == target){res.add(new ArrayList<>(path));return;}if (sum > target)return;// 多一步判断for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++){path.add(candidates[i]);sum += candidates[i];back(candidates, target, sum, i);sum -= candidates[i];path.removeLast();}}
}三、组合总和II
题目链接
思路:与组合总和类似,但区别于
本题candidates 中的每个数字在每个组合中只能使用一次。
本题数组candidates的元素是有重复的,而39.组合总和 (opens new window)是无重复元素的数组candidates。也就是说组合里的元素可能有重复且只使用一次,但组合之间不能重复。
本题的难点在于区别2中:集合(数组candidates)有重复元素,但还不能有重复的组合。
去重也去的是同一个树层上,重复的值。代码里就是判断i > startIndex && candidates[i] == candidates[i - 1],直接continue
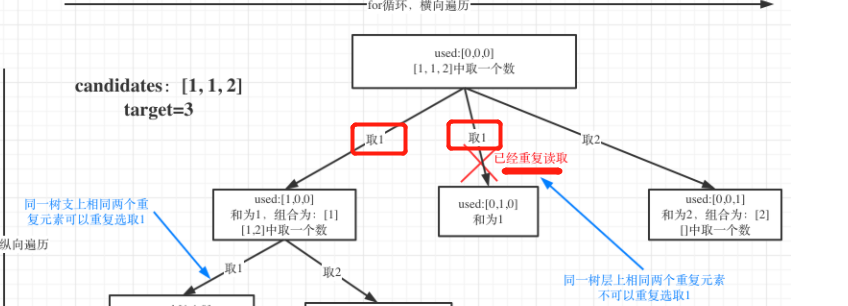
解法:
class Solution {List<List<Integer>> res = new ArrayList<>();LinkedList<Integer> path = new LinkedList<>();public List<List<Integer>> combinationSum2(int[] candidates, int target) {Arrays.sort(candidates); // 先进行排序back(candidates, target, 0, 0);return res;}private void back(int[] candidates, int target, int sum, int startIndex) {if (sum == target){res.add(new ArrayList<>(path));return;}if (sum > target)return;for (int i = startIndex; i < candidates.length && sum + candidates[i] <= target; i++){// 碰到同一树层重复元素 直接continueif ( i > startIndex && candidates[i] == candidates[i - 1] ) {continue;}path.add(candidates[i]);sum += candidates[i];back(candidates, target, sum, i + 1);sum -= candidates[i];path.removeLast();}}
}相关文章:

数据结构刷题(二十):17电话号码的字母组合、39组合总和、40组合总和II
一、电话号码的字母组合题目链接思路:回溯三部曲。确定回溯函数参数:题目中给的 digits,还要有一个参数就是int型的index(记录遍历第几个数字,就是用来遍历digits的,同时也代表了递归的深度)&am…...
)
Java面试总结(五)
sleep() 方法和 wait() 方法对比 相同点 两者都可以暂停线程的执行;两者都可以响应中断。 不同点 sleep()方法不会释放锁,wait()方法会释放锁; sleep()方法主要用于暂停线程的执行,wait()方法主要用于线程之间的交互/通信&…...
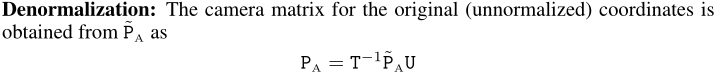
三维人脸实践:基于Face3D的渲染、生成与重构 <二>
face3d: Python tools for processing 3D face git code: https://github.com/yfeng95/face3d paper list: PaperWithCode 3DMM方法,基于平均人脸模型,可广泛用于基于关键点的人脸生成、位姿检测以及渲染等,能够快速实现人脸建模与渲染。推…...
在linux上部署Java项目
在Linux部署Java环境 要是想要部署java web程序,首先要配置环境 jdk tomcat mysql 安装jdk 推荐的方法是使用yum直接安装openjdk(开源的,与官方的jdk功能差不多),目前使用的最多的就是jdk8系列 yum list | grep jdk 在源上搜索所有关于jdk的文件 devel表示development的意思…...

线性表的接口
线性表的实现方式 顺序表 顺序表是一种线性表的实现方式,它是用一组地址连续的存储单元依次存储线性表中的数据元素,使得逻辑上相邻的元素在物理上也相邻⁴。顺序表可以用数组来实现,它的优点是可以快速定位第几个元素,但是缺点…...

spark三种操作模式的不同点分析
通常情况下,由于mapreduce计算引擎的效率问题,大部分公司使用的基本都是hive数仓spark计算引擎的方式搭建集群,所以对于spark的三种操作方式来进行简单的分析。在日常开发中,使用最多的方式取决于具体的需求和场景。以下是每种方式的一些常见用途:Spark …...
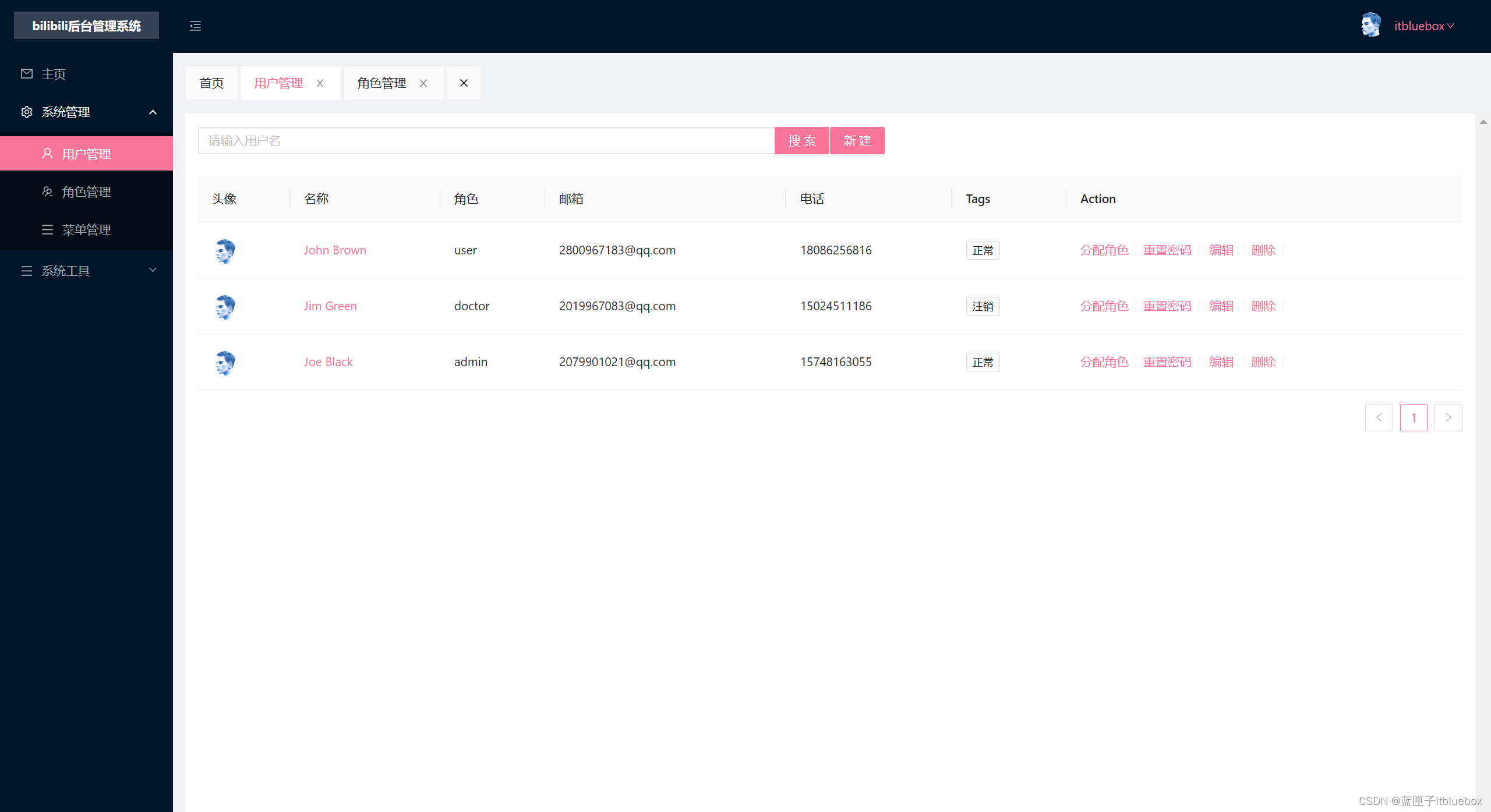
Vue3做出B站【bilibili】 Vue3+TypeScript【快速入门一篇文章精通系列(一)前端项目案例】
本项目分为二部分 1、后台管理系统(用户管理,角色管理,视频管理等) 2、客户端(登录注册、发布视频) Vue3做出B站【bilibili】 Vue3TypeScript【快速入门一篇文章精通系列(一)前端项目…...
)
猜数游戏--课后程序(Python程序开发案例教程-黑马程序员编著-第3章-课后作业)
实例10:猜数游戏 猜数游戏是一个古老的密码破译类、益智类小游戏,通常由两个人参与,一个人设置一个数字,一个人猜数字,当猜数字的人说出一个数字,由出数字的人告知是否猜中:若猜测的数字大于设…...

Nvidia jetson nano 部署yolov5_技术文档
Nvidia jetson nano 部署yolov5_技术文档 每天一句小姜格言:我行,我不是一般人儿 部署开始: 1、通过FileZilla,将window文件传输至jetson nano 上的nano文件夹下。 2、查看cuda 我买的jetson nano是带有配置好的镜像。系统配置…...

获取当前天数前N天
获取当前天数前N天 先封装到js里面 export const isTime (val) > {// 1.获取当前时间年月日时分秒格式xxxx-xx-xx xx:xx:xxvar myDate new Date() // 当前时间var y myDate.getFullYear() // 当前年份四位数var m myDate.getMonth() 1 < 10? 0 (myDate.getMont…...

Linux---基本指令
专栏:Linux 个人主页:HaiFan. 基本指令ls 指令pwd命令cd 指令touch指令mkdir指令(重要)rmdir指令 && rm 指令(重要)man指令(重要)cp指令(重要)mv指令…...
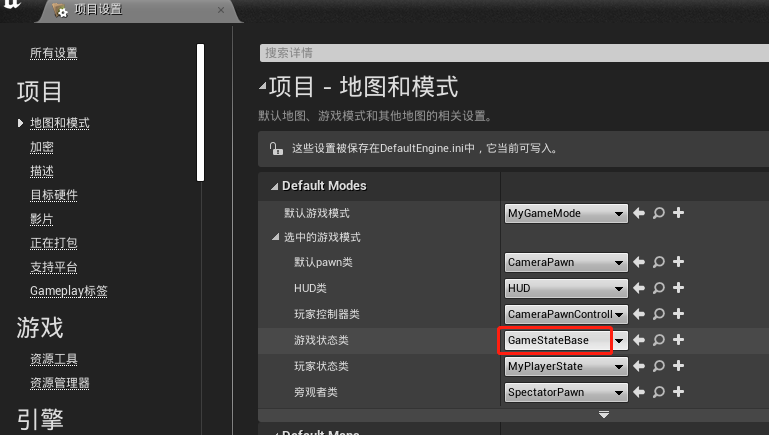
【UE4 RTS游戏】02-摄像机运动_完成摄像机在X轴上运动的相关步骤
效果通过控制键盘WS键使得“CameraPawn”进行前后移动步骤将landscape的Z轴位置更改为0删除“PostProcessVolume”将“LightmassImportanceVolume”移入Lighting文件夹内新建一个蓝图类,父类是Pawn,命名为“CameraPawn”将“MyController”重命名为“Cam…...
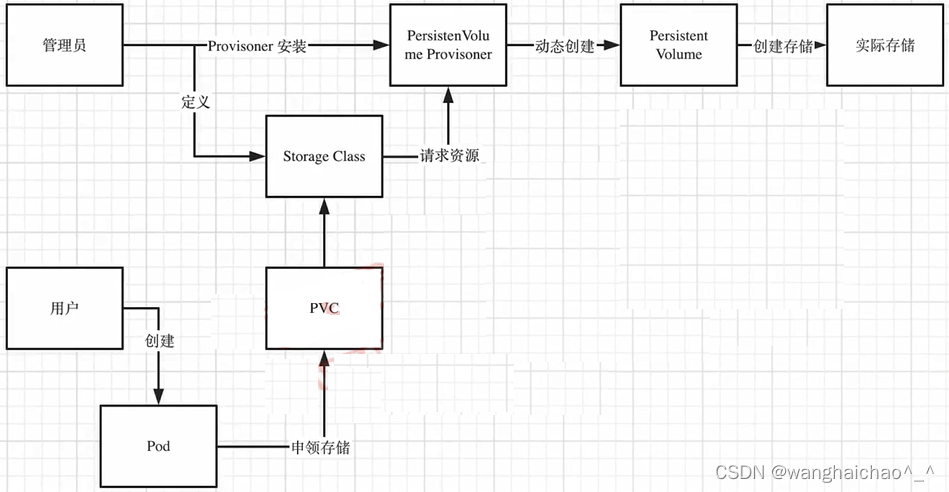
Kubernetes学习(五)持久化存储
Volume 卷 容器中的文件在磁盘上是临时存放的,这给容器中运行的特殊应用带来了一些问题。首先,当容器崩溃时,kubectl将重新启动容器,容器中的文件将会丢失--应为容器会以干净的状态重建。其次,当在一个Pod中运行多个容…...

下一个7年,保持期待、持续思考,酷雷曼继续向前!
过去7年,我们一直在思考, VR技术究竟能为我们的生活带来什么? 是足不出户就能云游千里的秀美风光? 是在家就能沉浸式体验线上消费的便利? 还是为商企和用户搭建更快速的沟通桥梁? NO.1、技术变革 在信…...

天梯赛训练L1-010--L1-012
目录 1、L1-010 比较大小 2、L1-011 A-B 3、L1-012 计算指数 4,一些题外话 1、L1-010 比较大小 分数 10 本题要求将输入的任意3个整数从小到大输出。 输入格式: 输入在一行中给出3个整数,其间以空格分隔。 输出格式: 在一…...
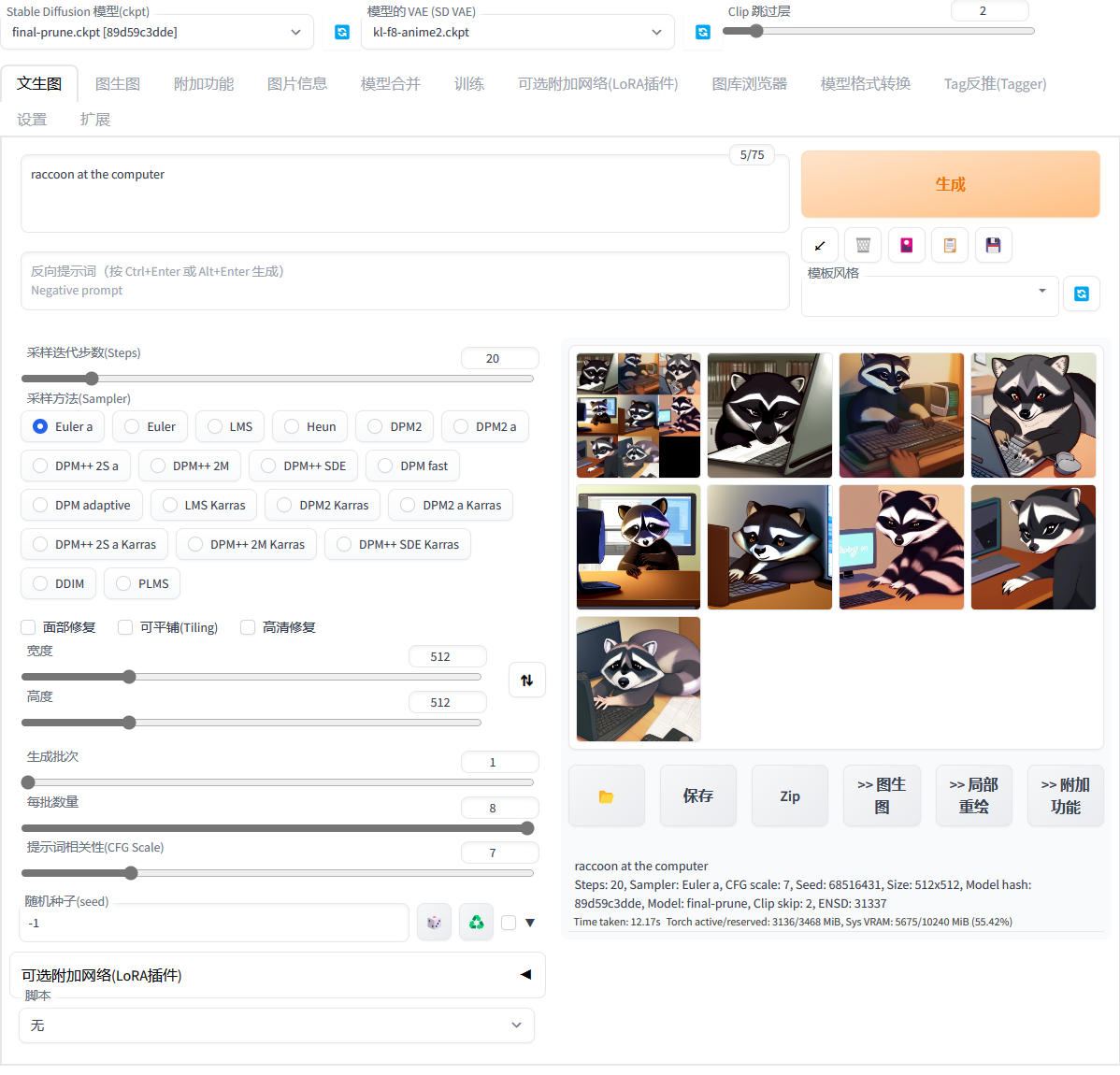
三分钟完成Stable Diffusion本地安装(零基础体验AI绘画)
三分钟完成Stable Diffusion本地安装前言安装步骤下载链接前言 最近AI绘画很火,很多无编程基础的小伙伴也想体验一下,所以写这篇博客来帮助小伙伴们愉快的体验一下~废话少说,我们直接开整! 安装步骤 首先,下载本项目的…...

电子台账:教程目录及软件下载
前面内容有点杂乱,这里整理一下教程目录。重点是制作模板,企业只要学会适合自己的一种就行。如果这些模板都学会做了,那可以当老师了。1 目录1 模板制作之一——列过滤(水平过滤)2 模板制作之二——行过滤(…...

多态的优势和弊端
目录 1.多态的优势 2.多态的弊端是什么? 3.引用数据类型的类型,转换有几种方式 4.强制类型转换能解决什么问题楠? 1.多态的优势 方法中,使用父类作为参数,可以接收所有子类的对象 package ploydemo3;import java.u…...

android h5考勤管理系统myeclipse开发mysql数据库编程服务端java计算机程序设计
一、源码特点 android h5考勤管理系统是一套完善的WEBandroid设计系统,对理解JSP java,安卓app编程开发语言有帮助(系统采用web服务端APP端 综合模式进行设计开发),系统具有完整的源代 码和数据库,系统主…...

第二道pwn题:shellcode
题目来自视频:链接:https://pan.baidu.com/s/17vX9dbfHkXBw71mcEXBgNQ?pwd6666 提取码:6666查看文件类型和保护,虽然现在的我还没有明白太多的保护。64位,放到ida里边rbp:保存的是栈中当前执行函数的基本地址。当前执…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

边缘计算网关提升水产养殖尾水处理的远程运维效率
一、项目背景 随着水产养殖行业的快速发展,养殖尾水的处理成为了一个亟待解决的环保问题。传统的尾水处理方式不仅效率低下,而且难以实现精准监控和管理。为了提升尾水处理的效果和效率,同时降低人力成本,某大型水产养殖企业决定…...

AWS vs 阿里云:功能、服务与性能对比指南
在云计算领域,Amazon Web Services (AWS) 和阿里云 (Alibaba Cloud) 是全球领先的提供商,各自在功能范围、服务生态系统、性能表现和适用场景上具有独特优势。基于提供的引用[1]-[5],我将从功能、服务和性能三个方面进行结构化对比分析&#…...

7种分类数据编码技术详解:从原理到实战
在数据分析和机器学习领域,分类数据(Categorical Data)的处理是一个基础但至关重要的环节。分类数据指的是由有限数量的离散值组成的数据类型,如性别(男/女)、颜色(红/绿/蓝)或产品类…...

python3GUI--基于PyQt5+DeepSort+YOLOv8智能人员入侵检测系统(详细图文介绍)
文章目录 一.前言二.技术介绍1.PyQt52.DeepSort3.卡尔曼滤波4.YOLOv85.SQLite36.多线程7.入侵人员检测8.ROI区域 三.核心功能1.登录注册1.登录2.注册 2.主界面1.主界面简介2.数据输入3.参数配置4.告警配置5.操作控制台6.核心内容显示区域7.检…...

深入理解JavaScript设计模式之闭包与高阶函数
目录 前言小序一场失败面试面试后的觉醒 闭包变量作用域:谁的地盘听谁的变量的生命周期:该走了,不该走的还在闭包的更多作用:不只是谈恋爱,还能干活!1、封装私有变量:你的变量我来守护2、延长变…...

JVM内存区域与溢出异常详解
当然可以。以下是结合了程序计数器和Java内存区域以及内存溢出异常的详细解释: JVM内存区域与内存溢出异常 Java虚拟机(JVM)管理着不同类型的内存区域,每个区域都有其特定的功能和可能导致的内存溢出异常。 程序计数器ÿ…...
