置信椭圆(误差椭圆)详解
文章目录
- Part.I 预备知识
- Chap.I 一些概念
- Chap.II 主成分分析
- Chap.III Matlab 函数 randn
- Chap.IV Matlab 函数 pca
- Part.II 置信椭圆的含义
- Chap.I 一个 Matlab 实例
- Sec.I 两个不相关变量的特征
- Sec.II 两个相关变量的特征
- Chap.II 变换阵 (解相关矩阵) 的求解
- Reference
Part.I 预备知识
Chap.I 一些概念
首先要了解一下下面的概念:
- 点估计:设总体
X的分布函数的形式已知,但它的一个或多个参数未知,借助于总体X的一个样本来估计总体未知参数的值的问题称为参数的点估计问题。 - 对于一个未知量,人们在测量或计算时,常不以得到近似值为满足,还需估计误差,即要求知道近似值的精确程度(亦即所求真值所在的范围)。类似地,对于未知参数 θ\thetaθ,除了求出它的点估计 θ^\hat \thetaθ^ 外,我们还希望估计出一个范围,并希望知道这个范围包含参数 θ\thetaθ 真值的可信程度。这样的范围通常以区间的形式给出,同时还给出此区间包含参数 θ\thetaθ 真值的可信程度。这种形式的估计称为区间估计,这样的区间即所谓置信区间。
- 置信区间:Confidence interval 设总体 X 的分布函数 F(x;θ)F(x;\theta)F(x;θ) 含有一个未知参数 θ\thetaθ,θ∈Θ\theta\in\Thetaθ∈Θ (Θ\ThetaΘ 是 θ\thetaθ 可能取值的范围),对于给定值 α\alphaα(0<α<10<\alpha<10<α<1),若由来自 X 的样本 X1,X2,⋯,XnX_1,X_2,\cdots,X_nX1,X2,⋯,Xn 确定的两个统计量 θ‾=θ‾(X1,X2,⋯,Xn)\underline \theta=\underline \theta(X_1,X_2,\cdots,X_n)θ=θ(X1,X2,⋯,Xn) 和 θ‾=θ‾(X1,X2,⋯,Xn)(θ‾<θ‾)\overline \theta=\overline \theta(X_1,X_2,\cdots,X_n)\ (\underline \theta<\overline \theta)θ=θ(X1,X2,⋯,Xn) (θ<θ) ,对于任意 θ<Θ\theta<\Thetaθ<Θ 满足 P{θ‾(X1,X2,⋯,Xn)<θ<θ‾(X1,X2,⋯,Xn)}≥1−αP\{\underline \theta(X_1,X_2,\cdots,X_n)<\theta<\overline \theta(X_1,X_2,\cdots,X_n)\}\ge1-\alphaP{θ(X1,X2,⋯,Xn)<θ<θ(X1,X2,⋯,Xn)}≥1−α,则称随机区间 (θ‾,θ‾)(\underline \theta,\overline \theta)(θ,θ) 是 θ\thetaθ 的置信水平为 1−α1-\alpha1−α 的置信区间,θ‾\underline \thetaθ 和 θ‾\overline \thetaθ 分别称为置信水平为 1−α1-\alpha1−α 的双侧置信区间的置信下限和置信上限,1−α1-\alpha1−α 称为置信水平。
- 上面给出了置信区间严格的数学定义,通俗的讲,置信区间展现的是这个参数的真实值有一定的带来落在测量结果的程度,其给出的是被量测参数的量测值的可信程度(置信水平),一般常用 95%95\%95% 置信水平。
- 68−95−99.768-95-99.768−95−99.7 法则:或者叫做 3σ3\sigma3σ 原则。对于正态分布,68%68\%68% 的数据分布在距离均值1个方差的范围;95%95\%95% 的数据分布在距离均值2个方差的范围;99.7%99.7\%99.7% 的数据分布在距离均值3个方差的范围内。
Chap.II 主成分分析
主成分分析 (Principal Component Analysis, PCA) 是一种统计方法,通过正交变换将一组可能存在相关性的变量转换为一组线性不相关的变量,转换后的这组变量叫主成分。PCA 的主要应用有:降维、特征提取、去噪、故障检测。
- PCA 的主要思想是将 nnn 维特征映射到 kkk 维上,这 kkk 维是全新的正交特征也被称为主成分,是在原有 nnn 维特征的基础上重新构造出来的 kkk 维特征。
- PCA 的工作就是从原始的空间中顺序地找一组相互正交的坐标轴,新的坐标轴的选择与数据本身是密切相关的。其中,第一个新坐标轴选择是原始数据中方差最大的方向,第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的,第三个轴是与第
1,2个轴正交的平面中方差最大的。依次类推,可以得到 nnn 个这样的坐标轴。通过这种方式获得的新的坐标轴,我们发现,大部分方差都包含在前面 kkk 个坐标轴中,后面的坐标轴所含的方差几乎为0。于是,我们可以忽略余下的坐标轴,只保留前面 kkk 个含有绝大部分方差的坐标轴。事实上,这相当于只保留包含绝大部分方差的维度特征,而忽略包含方差几乎为0的特征维度,实现对数据特征的降维处理。
Chap.III Matlab 函数 randn
下面的实例中会用到 Matlab 中生成正态分布随机数的函数randn(),下面对其用法做简要的介绍。
- randn:产生均值为0、方差为1的高斯白噪声,常用的用法有下面几种
randn(n):产生一个n*n的随机数方阵randn(m,n):产生一个m*n的随机数矩阵
除此之外还有,Matlab 关于随机数的生成函数还有:
rand:产生均值为0.5、幅度在0~1之间的伪随机数。randperm(n):产生1到n的均匀分布随机序列。normrnd(a,b,c,d):产生均值为a、方差为b大小为c*d服从正态分布的随机矩阵。
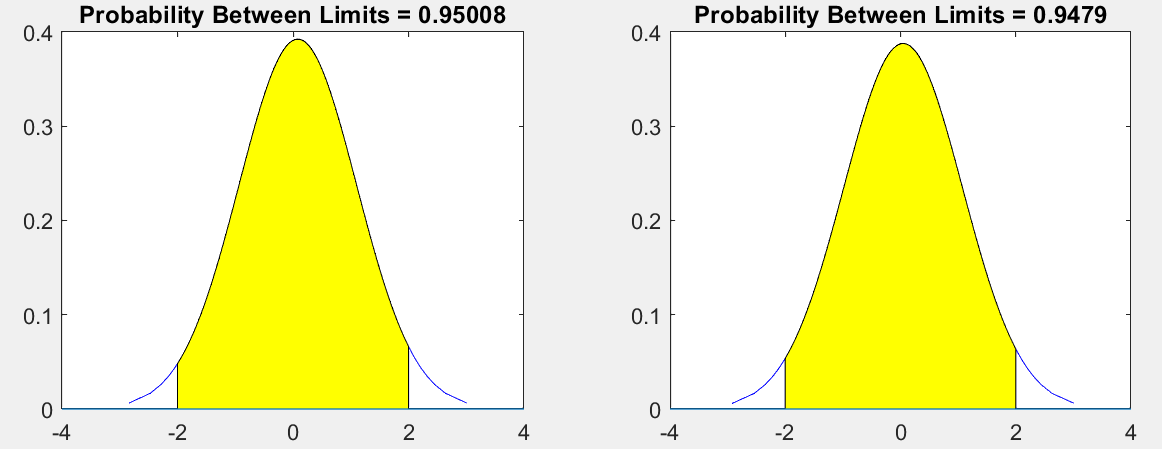
下面对randn做一个简单的验证:产生两列数据,分别画出它们的概率分布,看看图形是否符合正态分布。代码和绘制结果如下,可以看出结果符合预期。
%% 检验 randn 函数
function rTest()
data=randn(600,2);
figure
hold on
subplot(121)
t=2;
p=capaplot(data(:,1),[-t,t]);
subplot(122)
p=capaplot(data(:,2),[-t,t]);
end
Chap.IV Matlab 函数 pca
function [coeff, score, latent, tsquared, explained, mu] = pca(x,varargin)
输入:x 是样本,N*P=N个样本量,P维
输出:
- COEFF,返回
N×P数据矩阵X的主成分系数。X的行对应于观测值,列对应于变量。每列系数包含一个主成分的系数。各列按主成分方差(latent)降序排列。默认情况下,PCA将数据居中并使用奇异值分解算法。对于非默认选项,请使用名称/值对参数。 - SCORE,返回主成分得分,它是
X在主成分空间中的表示。score的行对应观察值,列对应主成分。中心数据可以用SCORE*COEFF重建。 - LATENT,返回每个主成分方差,即
X的协方差矩阵的特征值,特征值从大到小进行排序。 - TSQUARED,返回
X中每个观测值的Hotelling T平方统计值。PCA使用所有主分量计算TSQUARED(在整个空间中计算),即使请求的组件较少(请参见下面的“NumComponents”选项)。对于缩小空间中的TSQUARED,使用MAHAL(SCORE,SCORE)。 - EXPLAINED,返回一个向量,其中包含每个主成分方差占总方差的百分比。
- MU,
Centered设置为true时返回估计的平均值MU;设置为false时返回所有零。
Part.II 置信椭圆的含义
对于一维的情况,我们可以用置信区间来描述一个值落在某个区间(区域)的概率(置信水平),这个区间用几何表示是一个线段;对于二维的情况,几何意义上就从一条直线变成了一个平面,类似于置信区间,便有了置信椭圆(confidence ellipse)的概念。
下面是笔者的思考,一些自说自话罢了。
- 置信椭圆的概念是从置信区间类比而来的,严格意义上讲它描述的仅仅是二维的情况,对于三维可以称之为置信椭球,对于更高维可以称之为置信超椭球(自己瞎起的~);但是很多情况下,对于二维或者更高维,很多学者也将其称为置信椭圆。
- 为什么叫『椭圆』,不叫『圆』『长方形』呢?因为点的分布从图形上看,可以用一个椭圆将其包裹起来,所以叫椭圆。
- 『误差椭圆』这个概念又是怎么来的?对于二维情况,我们进行多次量测的目的是为了确定一个二维参数的取值,但是我们又不能 100%100\%100% 确定我们给出的值就是这个二位参数的真值,但是我们一般可以说这个二维参数有多少概率会落在某个范围内。在给定概率的情况下,这个范围越小,说明我们对我们的量测越有信心,我们量测的精度越高,误差越小。这个范围可以说是我们给出参数的精度或误差,所以便有了『误差椭圆』这个概念,这么说『精度椭圆』这个名词是不是也顺利成章了?
Chap.I 一个 Matlab 实例
其实,写这篇博文的初衷是为了搞清楚『为什么两个随机变量不相关,其误差椭圆的长轴平行于坐标轴』。还是看个例子,用数据说话吧。在看下面的内容之前首先要明确下面几点:
- 我们通过
randn函数来生成了两列均值为 0 方差为 1 的随机数;我们对这列随机数的理解为:每一列数据都表示对一个『代求量』的多次量测,显然我们已经假设我们的量测存在一个服从高斯分布的噪声,并且我们的『代求量』真值是0。我们也可以将每一列数据理解为对一个『随机变量』的多次抽样或观测。 randn函数虽然一次生成了两列数据,但是这两列数据是毫无关联的(当然也可以一次生成一列数据,分两次生成);换言之,这两列数据代表的两个『随机变量』是不相关的。
Sec.I 两个不相关变量的特征
首先用randn生成了两列均值为0、方差为1的随机数据,数据量是300*n;为了探究不同数据量的区别,因此画了6幅图如下,数据量分别是300*n,n=1,2,3,4,5,6。图中,len表示数据量的大小,a,b 分别表示椭圆长轴和短轴长度;红色和蓝色箭头(好吧,红色可能看不到箭头)分别表示长轴和短轴方向。可以看到,画出来的图形几近与圆,数据量越多,它越接近于圆。但是它的轴并不平行于坐标轴,可以这样解释:因为这两列数据的方差都是1,所以长短轴理论上应该相等,所以画出来的图形理论上应该是个圆(实际情况也是,数据量越多,它越接近于圆),所以其指向就无所谓了。
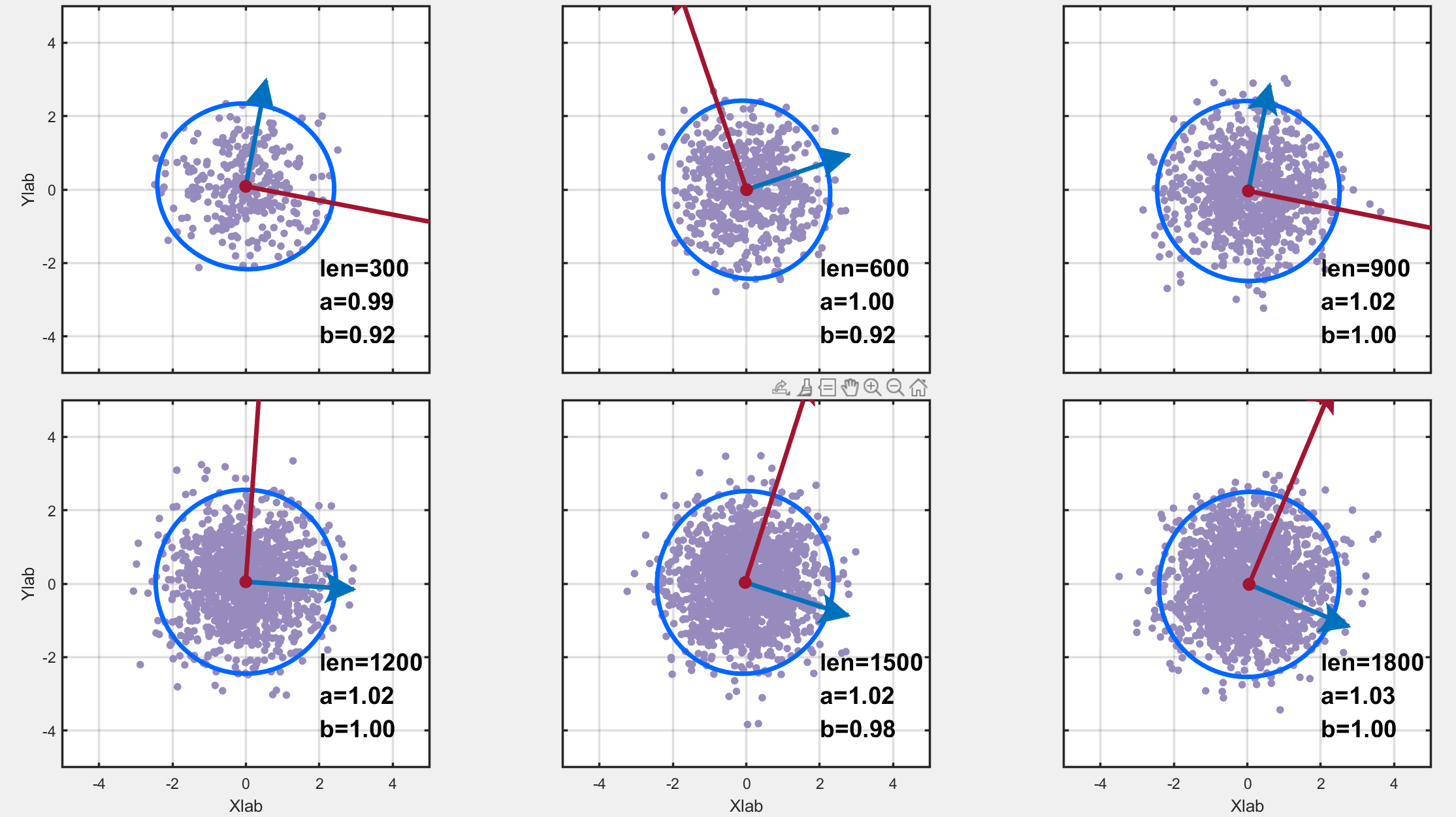
为了让两列数据的方差不同,我们将第一列数据乘上了2,不同数据量的绘图结果如下。可以看到,它确实是长短轴平行于坐标轴的椭圆!!
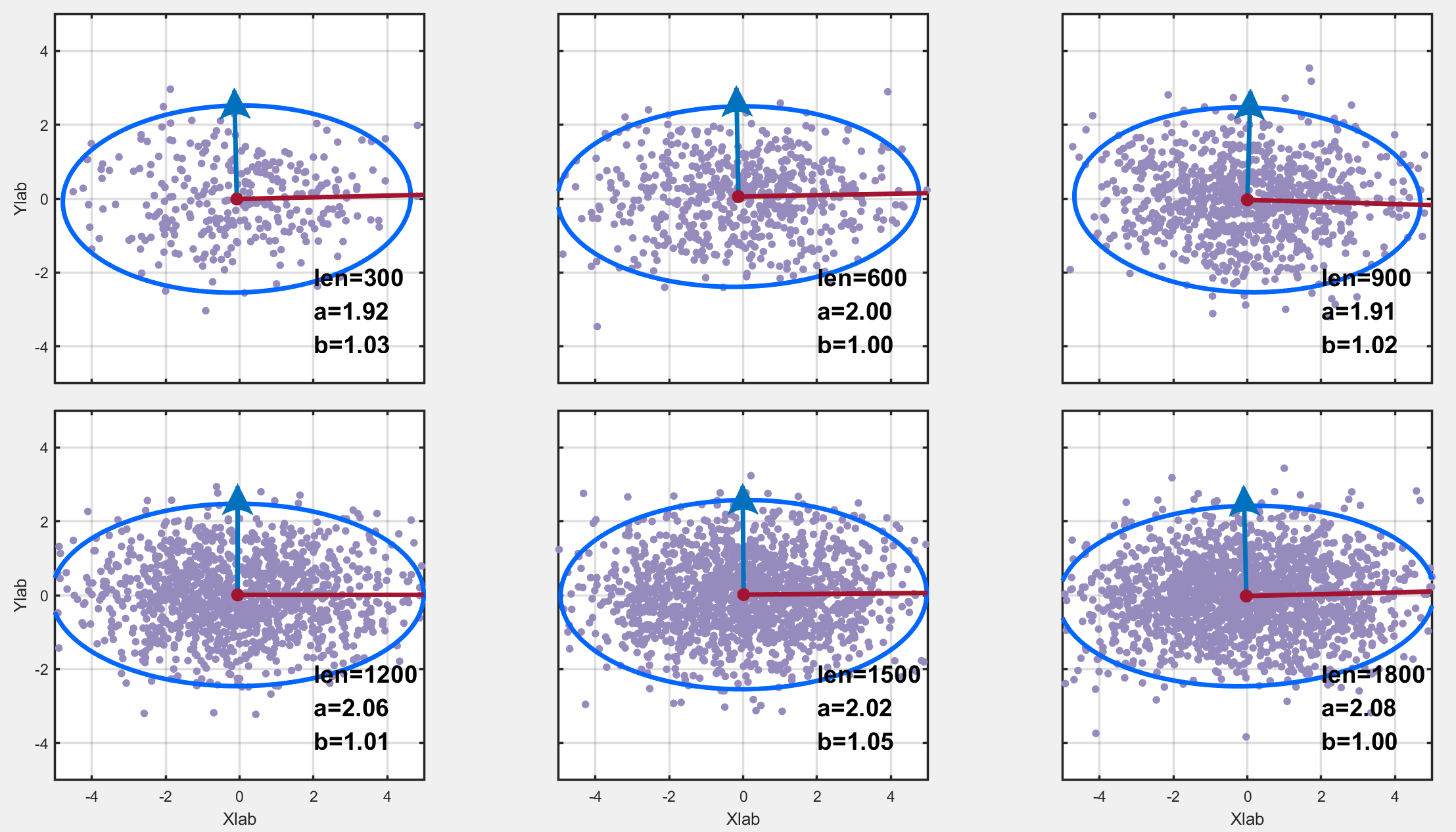
涉及的绘图代码如下:
%% 两个不相关变量的特性
function Test1(wid,hei,a,b)
figure
pmag=50; %the size of margin pix
marx(1:b+1,1)=3;marx(1)=8;
mary(1:a+1,1)=3;mary(1)=8;
sumx=sum(marx);sumy=sum(mary);
marx=marx./sumx;mary=mary./sumy;
lefy=pmag/hei/mary(1);
lefx=pmag/wid/marx(1);
marx=marx.*lefx;
mary=mary.*lefy;
wid1=(1-lefx)/b;
hei1=(1-lefy)/a;xt=-4:2:4;xtl1=sprintfc('%g',xt);xtl2=kcell(size(xtl1));xl=[-5 5];
yt1=-4:2:4;ytl1=sprintfc('%g',yt1);ytl2=kcell(size(ytl1));yl=[-5 5];set(gcf,'position',[0 0 wid hei])
for i=1:amagy=(a-i)*hei1+sum(mary(1:end-i));for j=1:bmagx=(j-1)*wid1+sum(marx(1:j));n=(i-1)*b+j;subplot(a,b,n);set(gca,'position',[magx magy wid1 hei1],'box','on');% plot here!len=300;data=randn(n*len, 2); % get the data PCA(data);set(gca,'XLim',xl,'XTick',xt,'XTicklabel',xtl2);set(gca,'YLim',yl,'YTick',yt1,'YTicklabel',ytl2);if j==1ylabel('Ylab');set(gca,'YTick',yt1,'YTicklabel',ytl1);endif i==axlabel('Xlab');set(gca,'XTick',xt,'XTicklabel',xtl1);endend
end
end% get a null cell which is a*b dims
function data=kcell(m)
a=m(1);b=m(2);
data=cell(a,b);
for i=1:afor j=1:bdata(i,j)=cellstr(num2str(data{i,j}));end
end
end%% PCA
function PCA(data)
len=size(data,1);
data(:,1)=2*data(:,1);
center = mean(data);
[coeff, ~, latent, ~, ~] = pca(data);% r1 r2 为自定义的向量大小参数(模)
r1 = 6;
r2 = 3;
% p1 p2 为第一主轴和第二主轴上的点
p1 = r1*coeff(:, 1)'+center;
p2 = r2*coeff(:, 2)'+center;% 主轴方向与X轴之间的夹角
angle = cart2pol(coeff(1, :), coeff(2, :))*180/pi;
beta = angle(1, 1);
% 置信椭圆坐标(以 95% 为例)
semimajor = sqrt(latent(1, 1)); % 长轴长度(一半)
semiminor = sqrt(latent(2, 1)); % 短轴长度(一半)
alpha = linspace(0, 360, 2000)';
% 卡方分布表
% https://people.richland.edu/james/lecture/m170/tbl-chi.html
% level = 4.605; % 90%
level = 5.991; % 95%
% level = 9.210; % 99%
% 椭圆坐标点
ellipse_X = center(1, 1)+sqrt(level)*(semimajor*cosd(alpha)*cosd(beta)-...semiminor*sind(alpha)*sind(beta));
ellipse_Y = center(1, 2)+sqrt(level)*(semimajor*cosd(alpha)*sind(beta)+...semiminor*sind(alpha)*cosd(beta));%% 可视化
% figure
hold on
box on
grid on
% 原始数据
scatter(data(:, 1), data(:, 2), 15, 'LineWidth', 1.2,...'MarkerEdgeColor', [151, 138, 189]/255,...'MarkerFaceColor', [151, 138, 189]/255);
xlim([-5, 5]);
ylim([-5, 5]);
set(gca, 'linewidth', 1.5)% 置信椭圆
plot(ellipse_X, ellipse_Y, 'Color', [0, 102, 255]/255,...'LineStyle', '-', 'LineWidth', 3),% 第一主轴方向
arrow_1 = annotation('arrow', 'Color', [162, 20, 47]/255,...'HeadStyle', 'cback2', 'LineWidth', 3, 'HeadWidth', 20, 'HeadLength', 20);
arrow_1.Parent = gca;
arrow_1.X = [center(1, 1), p1(1, 1)];
arrow_1.Y = [center(1, 2), p1(1, 2)]; % 第二主轴方向
arrow_2 = annotation('arrow', 'Color', [0, 114, 189]/255,...'HeadStyle', 'cback2', 'LineWidth', 3, 'HeadWidth', 20, 'HeadLength', 20);
arrow_2.Parent = gca;
arrow_2.X = [center(1, 1), p2(1, 1)];
arrow_2.Y = [center(1, 2), p2(1, 2)]; % 中心点
plot(center(1, 1), center(1, 2),...'Marker', 'o',...'MarkerSize', 8,...'MarkerEdgeColor', [162, 20, 47]/255,...'MarkerFaceColor', [162, 20, 47]/255);% title('主轴方向和置信椭圆', 'FontSize', 16, 'FontWeight', 'bold')
str=sprintf('len=%d\na=%.2f\nb=%.2f',len,semimajor,semiminor);
text(2, -3, str, 'FontSize', 16, 'FontWeight', 'bold')
axis equal
end
Sec.II 两个相关变量的特征
为了让两个随机变量相关,我们记randn生成的两列数据为 X=[a,b]X=[a,b]X=[a,b](其中 aaa 的均值为0,方差为2;bbb 的均值为0,方差为1),将其乘上一个矩阵得到新的数据 YYY:
Y=[a′,b′]=[a,b]⋅[11−12]=X⋅ZY=[a',b']=[a,b]\cdot \left[ \begin{array}{ccc} 1 & 1 \\ -1 & 2 \\ \end{array} \right]=X\cdot ZY=[a′,b′]=[a,b]⋅[1−112]=X⋅Z
也就是说,a′=a−b,b′=a+2ba'=a-b,\ b'=a+2ba′=a−b, b′=a+2b,然后我们绘制其置信椭圆如下图所示:
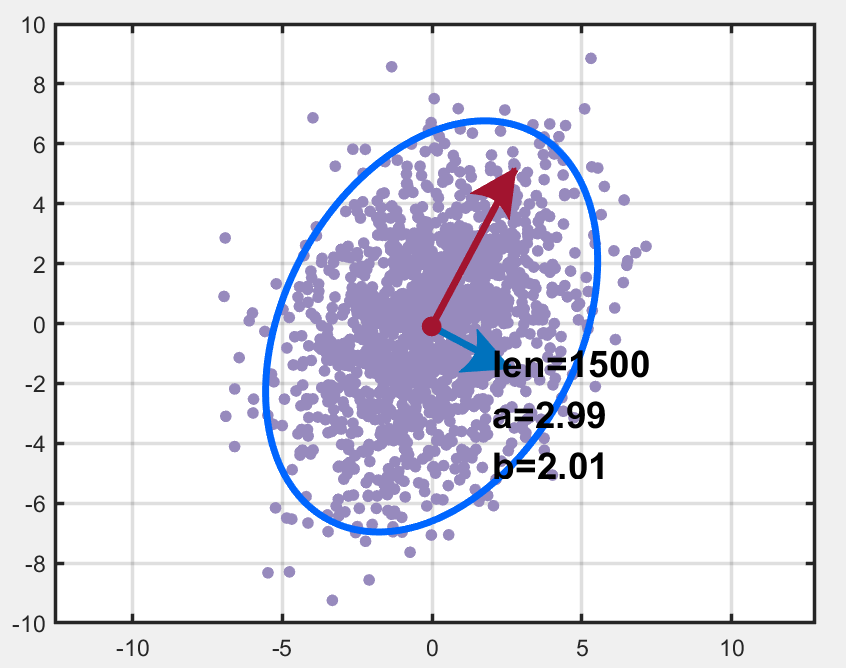
其代码如下:
%% 两个相关变量的特征
function Test2()
len=300;
data=randn(5*len, 2); % get the data
data(:,1)=2*data(:,1); % 第一列方差变为2
data1=zeros(size(data));
Z=[1 1;-1 2];
data1=data*Z;
% data1(:,1)=data(:,1)-data(:,2);
% data1(:,2)=data(:,1)+2*data(:,2);
PCA(data1);
end
我们能让两个不相关的随机变量通过乘以一个矩阵变成相关的;同样的我们也可以通过乘一个矩阵使它们『解相关』。对于这组数据,我们已经知道了使它俩变成相关的矩阵 ZZZ,那么再乘 Z−1Z^{-1}Z−1 显然可以解相关;但是对于一个我们不知道变换矩阵(对应此例也就是上文的 Z−1Z^{-1}Z−1 ) 的数据,我们一般用下面的方法来求『变换阵』。
PS:之前的我还以为用 LU 分解来求变换阵,并且认为求解变换阵的方法是『高斯变换』,变换阵被称为『高斯变换阵』。但是并不是,是通过特征值和特征向量来求的。
Chap.II 变换阵 (解相关矩阵) 的求解
现在的问题是:已知两个随机变量的许多量测(两列数据),而且这两个随机变量是相关的;怎么找到一个矩阵,使得这两列数据乘上这个矩阵之后,这两列数据就不相关了。笔者觉得有两种方法:一种是几何意义上的:将置信椭圆旋转一下,使得其长短轴平行于坐标轴(旋转在代数意义上乘以一个矩阵);另一种是纯代数:通过矩阵变换找到这样的旋转矩阵。
实际上,上述问题用主成分分析找主元、降相关就可以解决。
基于特征值分解协方差矩阵实现 PCA 算法步骤
- 输入数据集 X={x1,x2,⋯,xn}X=\{x_1,x_2,\cdots,x_n\}X={x1,x2,⋯,xn},需要将其降到 kkk 维
- 去中心化:每一维特征减去各自的均值
- 计算方差-协方差矩阵 A=1nXTXA=\frac{1}{n}X^TXA=n1XTX (这里分母是 nnn 或 n−1n-1n−1 对求出的特征向量没有影响)
- 求出 AAA 的特征值和特征向量
- 对特征值从大到小排序,选择其中最大的 kkk 个。然后将其对应的 kkk 个特征向量分别作为行向量组成特征向量矩阵 PPP
- 将数据转换到 kkk 个特征向量构建的新空间中,即 Y=PXY=PXY=PX
下面对此种方法求『解相关矩阵』进行一个简单的证明。
- 首先要明确,我们的目的是将 XXX 的协方差矩阵 AAA 转换为一个对角阵,即 XTX=A=VTΛVX^TX=A=V^T\Lambda VXTX=A=VTΛV,也就是令 (XV−1)T(XV−1)=Λ(XV^{-1})^T(XV^{-1})=\Lambda(XV−1)T(XV−1)=Λ,即寻求一个转换阵 Z=V−1Z=V^{-1}Z=V−1,使得 BTB=Λ(B=XZ)B^TB=\Lambda\ (B=XZ)BTB=Λ (B=XZ)
- 关于矩阵分解的方法中,哪种分解方法可以使得矩阵的分解结果中含有一个对角阵呢?奇异值SVD和特征分解分解可以!用这两种分解中的哪种都可以!
- 特征分解:A=VΛV−1A=V\Lambda V^{-1}A=VΛV−1 并且协方差阵是一个实对称阵,对于实对称阵,其不同特征值对应的特征向量正交。又因为特征向量伸缩(乘一个常数)之后还是特征向量,所以我们很容易构造出来一个特征向量矩阵 VVV,使得 VT=V−1V^T=V^{-1}VT=V−1.
- 基于上述,有 XTX=VΛV−1X^TX=V\Lambda V^{-1}XTX=VΛV−1. 所以我们取转换阵 Z=VZ=VZ=V 令 Y=XZY=XZY=XZ,YTY=VTXTXV=VTVΛV−1V=V−1VΛV−1V=ΛY^TY=V^TX^TXV=V^TV\Lambda V^{-1}V=V^{-1}V\Lambda V^{-1}V=\LambdaYTY=VTXTXV=VTVΛV−1V=V−1VΛV−1V=Λ。这样利用转换阵 VVV 便将协方差矩阵变成了对角阵,即实现了『解相关』。
基于上述步骤,对于相关变量得到了其变换阵 X1X1X1,绘图结果如下,左上是原始数据,左下和右上对应中可行的转换矩阵,右下啥也不是。我们发现得到的变换阵 X1X1X1 并不是 Z−1Z^{-1}Z−1 (DataY=DataX⋅ZData_Y=Data_X\cdot ZDataY=DataX⋅Z),这说明变换阵不唯一?
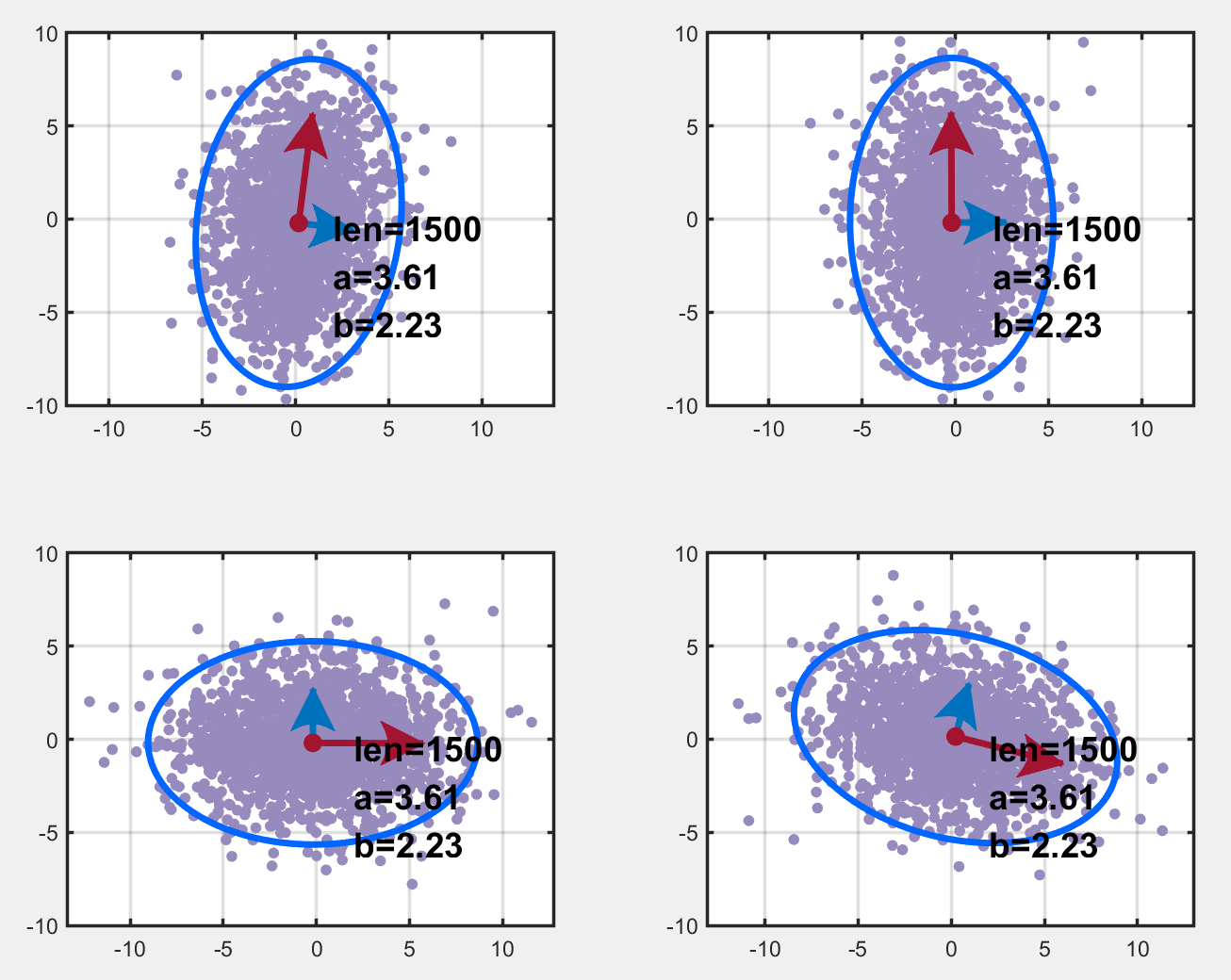
代码如下:
%% PCA 求 变换矩阵 并绘图
function Test3()
len=300;
data=randn(5*len, 2); % get the data
data(:,1)=2*data(:,1); % 第一列方差变为2
Z=[1 1;-1 3];
data1=data*Z;
A=data1'*data1/(5*len);
[X,D]=eig(A); % 求特征值 D 和特征向量 X; X 各列是相应的特征向量
% A*X(:,1)-D(1,1)*X(:,1)
data2=data1*X;
X1=[X(:,2),X(:,1)]; % 因为第一个特征值比较大,所以优先将第一个特征向量放在前面
data3=data1*X1;
data4=data1*X1';
% Plot
subplot(2,2,1);
PCA(data1); % 原始数据
subplot(2,2,2);
PCA(data2); % 去相关之后的 y 轴长
subplot(2,2,3);
PCA(data3); % 去相关之后的 x 轴长
subplot(2,2,4);
PCA(data4); % 啥也不是
end
PS:实际上,笔者使用的 PCA 函数中已经做了主成分分析(求出了样本的方差-协方差矩阵),里面用的是Matlab自带的pca函数,为了更详细地了解 PCA 的过程,笔者又做了点额外工作,PCA 函数在本博文中仅仅发挥一个画图的功能。
Reference
- 主成分分析 (PCA) 的主轴和置信椭圆可视化
- 主成分分析(PCA)原理详解
- PCA的数学原理
- 置信椭圆与R画法
- Matlab 让多图排版更美观
- 矩阵的各种分解汇总
- 注:上面的代码已经很全了,笔者也提供了测试时所使用的
.m文件,戳我下载。
相关文章:

置信椭圆(误差椭圆)详解
文章目录Part.I 预备知识Chap.I 一些概念Chap.II 主成分分析Chap.III Matlab 函数 randnChap.IV Matlab 函数 pcaPart.II 置信椭圆的含义Chap.I 一个 Matlab 实例Sec.I 两个不相关变量的特征Sec.II 两个相关变量的特征Chap.II 变换阵 (解相关矩阵) 的求解ReferencePart.I 预备知…...

FreeSWITCH 智能呼叫流程设计
文章目录1. 智能呼叫流程2. 细节处理1. 呼叫字符串指定拨号计划2. 外呼的拨号计划3. 语音打断的支持1. 智能呼叫流程 用户与机器人对话通常都是以文本的形式进行,但是借助 ASR 和 TTS 技术,以语音电话为载体的智能呼叫系统成为可能。智能呼叫系统涉及到…...

什么是Restful风格
什么是RestFul风格? Restful就是一个资源定位及资源操作的风格。不是标准也不是协议,只是一种风格。基于这个风格设计的软件可以更简洁,更有层次,更易于实现缓存等机制。 REST即Representational State Transfer的缩写࿰…...

sumifs的交叉 表的例子
比如这样,那么冰箱绿山店的栏位中,SUMIFS($D$3:$D$10,$B$3:$B$10,$F3,$C$3:$C$10,G$2)就是把求和范围,条件1设置为固定列的复合引用,条件2设置为固定行的复合引用即可。...

React :一、简单概念
目录 1.什么是React? 2.谁开发的 3.为什么要学React? 4.React的特点? 5.React依赖包 6.第一个React程序 7.虚拟DOM的两种创建方法 8.虚拟DOM和真实DOM 1.什么是React? 用于构建用户界面的JavaScript库,是一个将…...
Actipro WinForms Studio Crack
Actipro WinForms Studio Crack 已验证Microsoft.NET 7兼容性。 添加了MetroDark配色方案。 添加了支持MetroLight和MetroDark颜色方案的MetroScrollBarRenderer。 添加了IWindowsColorScheme接口,该接口将替换对WindowsColorScheme的大多数引用。 添加了IWindowsCo…...
英伦四地到底是什么关系?
英格兰、苏格兰、威尔士和北爱尔兰四地到底是什么关系,为何苏格兰非要独立?故事还要从中世纪说起。大不列颠岛位于欧洲西部,和欧洲大陆隔海相望。在古代,大不列颠岛和爱尔兰属于凯尔特人的领地。凯尔特人是欧洲西部一个庞大的族群…...
Google三大论文之GFS
Google三大论文之GFS Google GFS(Google File System) 文件系统,一个面向大规模数据密集型应用的、可伸缩的分布式文件系统。GFS 虽然运行在廉价的普遍硬件设备上,但是它依然了提供灾难冗余的能力,为大量客户机提供了…...
嵌入式安防监控项目——exynos4412主框架搭建
目录 一、模块化编程思维 二、安防监控项目主框架搭建 一、模块化编程思维 其实我们以前学习32使用keil的时候就是再用模块化的思维。每个硬件都单独有一个实现功能的C文件和声明函数,进行宏定义以及引用需要使用头文件的h文件。 比如简单的加减乘除取余操作我们…...

YOLOv5s网络模型讲解(一看就会)
文章目录前言1、YOLOv5s-6.0组成2、YOLOv5s网络介绍2.1、参数解析2.2、YOLOv5s.yaml2.3、YOLOv5s网络结构图3、附件3.1、yolov5s.yaml 解析表3.2、 yolov5l.yaml 解析表总结前言 最近在重构YOLOv5代码,本章主要介绍YOLOv5s的网络结构 1、YOLOv5s-6.0组成 我们熟知YO…...

kkfileView linux 离线安装
文章目录前言一、安装 LiberOffice二、安装kkfileView1.下载安装包2.启动总结前言 一、安装 LiberOffice 下载https://kkfileview.keking.cn/LibreOffice_7.1.4_Linux_x86-64_rpm.tar.gz 安装 tar -zxvf LibreOffice_7.1.4_Linux_x86-64_rpm.tar.gz cd LibreOffice_7.1.4.2_L…...

如何编写BI项目之ETL文档
XXXXBI项目之ETL文档 xxx项目组 ------------------------------------------------1---------------------------------------------------------------------- 目录 一 、ETL之概述 1、ETL是数据仓库建构/应用中的核心…...

【LeetCode】剑指 Offer 24. 反转链表 p142 -- Java Version
题目链接:https://leetcode.cn/problems/fan-zhuan-lian-biao-lcof/submissions/ 1. 题目介绍(24. 反转链表) 定义一个函数,输入一个链表的头节点,反转该链表并输出反转后链表的头节点。 【测试用例】: 示…...
LAY-EXCEL导出excel并实现单元格合并
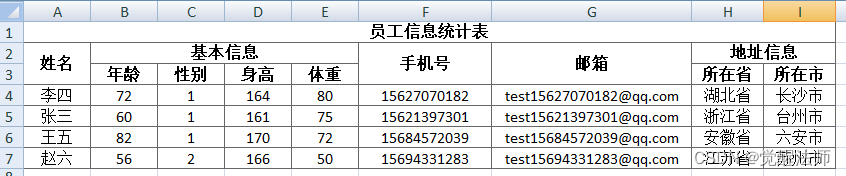
通过lay-excel插件实现Excel导出,并实现单元格合并,样式设置等功能。更详细描述,请去lay-excel插件文档查看,地址:http://excel.wj2015.com/_book/docs/%E5%BF%AB%E9%80%9F%E4%B8%8A%E6%89%8B.html一、安装这里使用Vue…...

配置VM虚拟机Centos7网络
配置VM虚拟机Centos7网络 第一步,进入虚拟机设置选中【网络适配器】选择【NAT模式】 第二步,进入windows【控制面板\网络和 Internet\网络连接】设置网络状态。 我们选择【VMnet8】 点击【属性】查看它的网络配置 2 .我们找到【Internet 协议版本 4(TCP…...
Kafka 位移主题
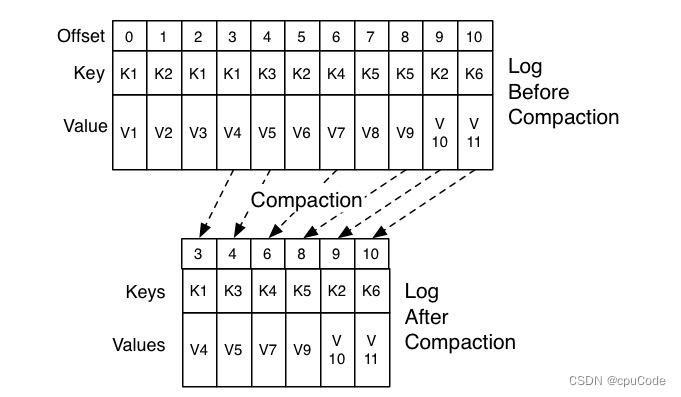
Kafka 位移主题位移格式创建位移提交位移删除位移Kafka 的内部主题 (Internal Topic) : __consumer_offsets (位移主题,Offsets Topic) 老 Consumer 会将位移消息提交到 ZK 中保存 当 Consumer 重启后,能自动从 ZK 中读取位移数据,继续消费…...
详细讲解零拷贝机制的进化过程
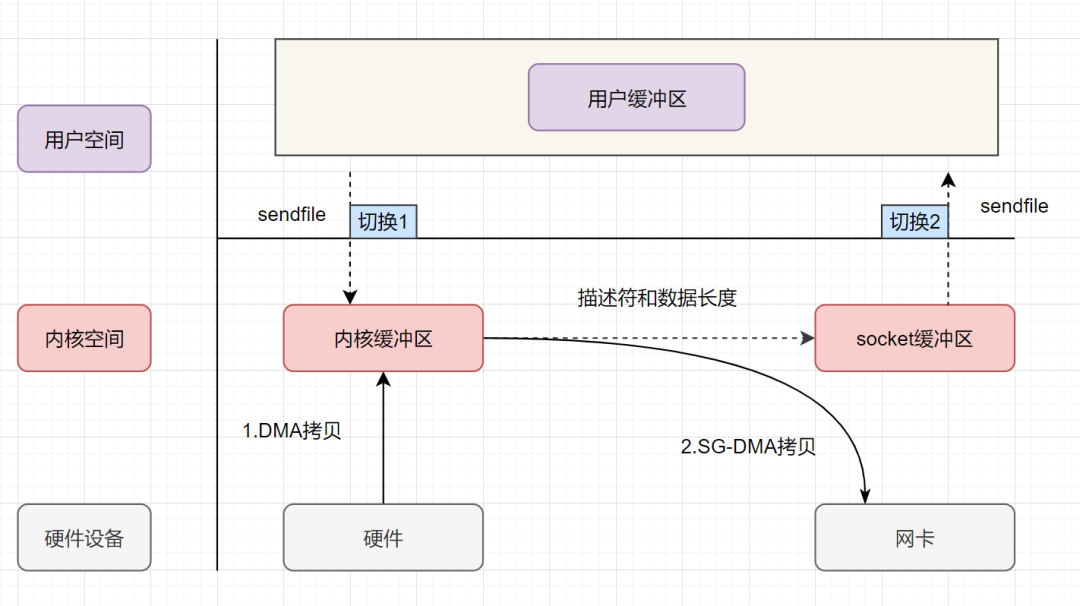
一、传统拷贝方式(一)操作系统经过4次拷贝CPU 负责将数据从磁盘搬运到内核空间的 Page Cache 中;CPU 负责将数据从内核空间的 Page Cache 搬运到用户空间的缓冲区;CPU 负责将数据从用户空间的缓冲区搬运到内核空间的 Socket 缓冲区…...

2023年场外个股期权研究报告
第一章 概况 场外个股期权(Over-the-Counter Equity Option),是指由交易双方根据自己的需求和意愿,通过协商确定行权价格、行权日期等条款的股票期权。与交易所交易的标准化期权不同,场外个股期权的合同内容可以根据交…...

k8s pod,ns,pvc 强制删除
一、强制删除pod$ kubectl delete pod <your-pod-name> -n <name-space> --force --grace-period0解决方法:加参数 --force --grace-period0,grace-period表示过渡存活期,默认30s,在删除POD之前允许POD慢慢终止其上的…...

力扣第99场双周赛题目记录(复盘)
第一题 2578.最小和分割 给你一个正整数 num ,请你将它分割成两个非负整数 num1 和 num2 ,满足: num1 和 num2 直接连起来,得到 num 各数位的一个排列。 换句话说,num1 和 num2 中所有数字出现的次数之和等于 num 中所…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

破解路内监管盲区:免布线低位视频桩重塑停车管理新标准
城市路内停车管理常因行道树遮挡、高位设备盲区等问题,导致车牌识别率低、逃费率高,传统模式在复杂路段束手无策。免布线低位视频桩凭借超低视角部署与智能算法,正成为破局关键。该设备安装于车位侧方0.5-0.7米高度,直接规避树枝遮…...

绕过 Xcode?使用 Appuploader和主流工具实现 iOS 上架自动化
iOS 应用的发布流程一直是开发链路中最“苹果味”的环节:强依赖 Xcode、必须使用 macOS、各种证书和描述文件配置……对很多跨平台开发者来说,这一套流程并不友好。 特别是当你的项目主要在 Windows 或 Linux 下开发(例如 Flutter、React Na…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

当下AI智能硬件方案浅谈
背景: 现在大模型出来以后,打破了常规的机械式的对话,人机对话变得更聪明一点。 对话用到的技术主要是实时音视频,简称为RTC。下游硬件厂商一般都不会去自己开发音视频技术,开发自己的大模型。商用方案多见为字节、百…...
