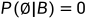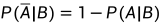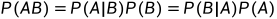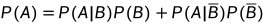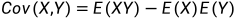概率论与数理统计相关知识
本博客为《概率论与数理统计--茆诗松(第二版)》阅读笔记,目的是查漏补缺
前置知识
数学符号
连乘符号: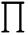 ;总和符号:
;总和符号: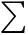 ;“任意”符号:∀;“存在”符号:∃
;“任意”符号:∀;“存在”符号:∃
第一章:随机事件及其概率
随机事件及基础定义
随机现象所有基本结果的全体称为这个随机现象的基本空间。常用Ω={w}表示,其中元素w就是基本结果。在统计学中,基本结果w 是抽样的基本单元,故基本结果又称为样本点,基本空间又称为样本空间。
随机事件:随机现象某些基本结果组成的集合,称为随机事件,简称事件。事件的关系:包含(A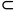 B)、并(A
B)、并(A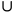 B)、交(A
B)、交(A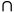 B)、不相容、对立(
B)、不相容、对立(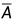 )。
)。
两个事件的独立性:对任意两个事件 A与B,若有 P(AB)=P(A)P(B),则称事件A与B相互独立简称A与B独立。否则称事件A与B不独立。
多个事件的独立性:

条件概率
条件概率的一般定义如下:(P(A)与P(A|B)不同,本质上是事件B的发生,改变了基本空间,从而改变了P(A))

条件概率的性质:
条件概率是概率,首先满足概率的三条公理:
非负性:P(A|B)≥0
正则性:P(Ω|B)=1
可加性:假如事件A1与A2互不相容,且P(B)>0,则:
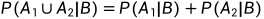
由三条公理,可推出满足以下性质:
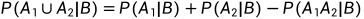 (对于任意的A1、A2而言,不再需要二者不相容)
(对于任意的A1、A2而言,不再需要二者不相容)
当B=Ω时,条件概率转化为无条件概率。
特殊性质:
乘法公式:任意两个事件的交的概率等于一事件的概率乘以在这事件已发生条件下另一事件的条件概率,只要它们的概率都不为零即可。第一个等式成立要求P(B)>0,第二个等式成立要求P(A)>0
假如事件A与B独立,且P(B)>0,则有:
 。反之亦然。
。反之亦然。
一般乘法公式:
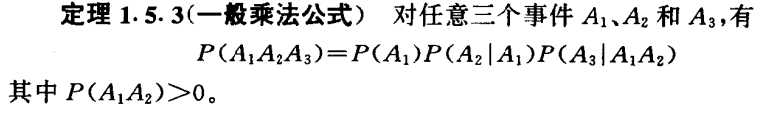
贝叶斯公式
全概率公式:设A与B是任意两个事件,假如,则
贝叶斯公式(由全概率公式推出):意思就是P(B_i)已知,且P(A|B_i)可以通过试验等手段获得,则通过贝叶斯公式可以计算在给定事件A的情况下,任意事件B_i发生的条件概率。

第二章:随机变量及其概率分布
随机变量
随机变量分为:离散随机变量、连续随机变量
累积概率分布函数(CDF)

离散、连续随机变量都有各自的分布函数。
分布函数F(x)的基本性质:

离散随机变量
离散随机变量常用分布列来表示概率分布(分布列还有两种图表示方法:线条图与概率直方图):

常见的离散分布有:二项分布、泊松分布等
二项分布
贝努里实验:只有两个结果(成功与失败)的试验。
n重贝努里实验:由n次相同的、独立的贝怒里试验组成的随机试验称为n重贝努里实验。
设X为n重贝努里实验成功的次数,则随机变量X可能取值为:0,1,…,n,其概率分布为:
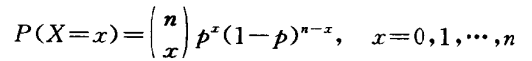
在概率论中,称随机变量X服从二项分布 b(n, p) , 并记作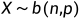 。二项分布的数学期望 :
。二项分布的数学期望 :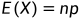
泊松分布
若随机变量服从泊松分布,即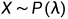 ,这意味着X仅取0,1,2,…等一切非负整数,且取这些值的概率为:
,这意味着X仅取0,1,2,…等一切非负整数,且取这些值的概率为:

泊松分布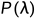 的数学期望就是参数 λ。
的数学期望就是参数 λ。
连续随机变量
概率密度函数(PDF)
连续随机变量不能再用分布列来表示,而要改用概率密度函数(就是连续的概率曲线),数学定义如下:

连续随机变量的分布函数F(x)可以用其密度函数p(x)表示出来:

连续随机变量:分布函数F(x)是密度函数p(x)的积分,密度函数p(x)是分布函数F(x)的求导
连续随机变量的数学期望:

数学期望E(X)的总结:

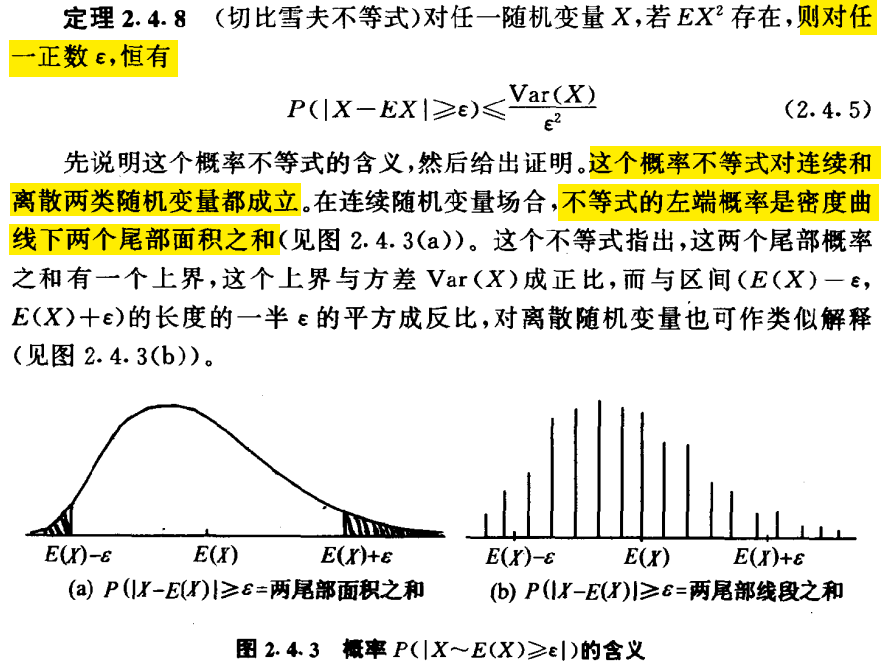
连续随机变量常见的分布有:正态分布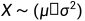
方差
在概率论和统计学中,数学期望E(X)是分布的位置特征数,它总位于分布的中心,随机变量X的取值总在其周围波动。
方差是度量随机变量X和其数学期望(E(X),即均值)之间的偏离程度( 称X-E(X)为偏差)的特征数,即度量随机变量X的离散程度,定义如下:

切比雪夫不等式
切比雪夫不等式对连续和离散两类随机变量都成立,定义如下:
第三章:多维随机变量
联合分布函数
在有些随机现象中,每个基本结果w只用一个随机变量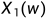 描述是不够的,而要同时用多个,譬如同时用n 个随机变量
描述是不够的,而要同时用多个,譬如同时用n 个随机变量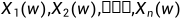 ,去描述。
,去描述。
多维随机变量的概率分布可以用联合分布函数来表示,定义如下:
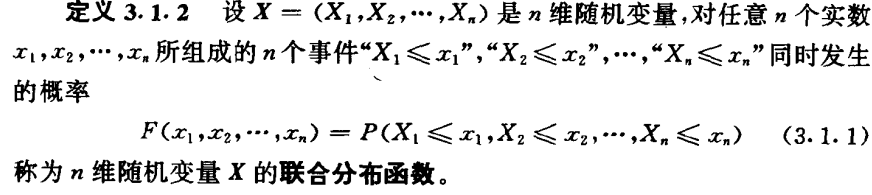
对于联合分布函数 ,使一个随机变量比如
,使一个随机变量比如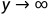 ,则可以得到另一个变量的分布函数
,则可以得到另一个变量的分布函数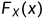 (或
(或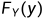 ),称为联合分布函数
),称为联合分布函数 的边缘分布函数,简称边缘分布。
的边缘分布函数,简称边缘分布。
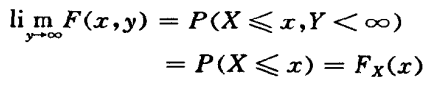
对于多维连续随机变量(以二维为例),其联合分布函数如下:
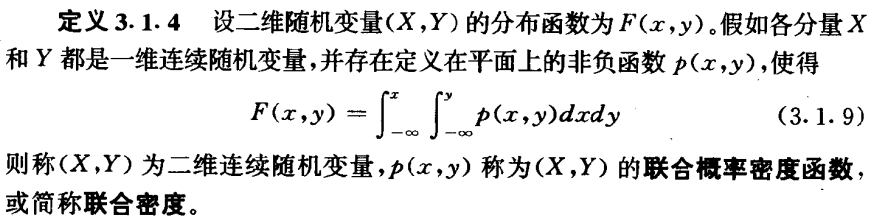
条件分布和边缘密度函数
连续随机变量的条件分布:(X,Y)是二维连续随机变量,p(x,y)是其联合密度函数,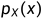 和
和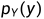 是其边缘密度函数。
是其边缘密度函数。
在给定Y=y下X的条件密度函数为: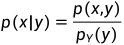
在给定X=x下Y的条件密度函数为: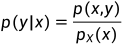
构造联合分布p(x,y)
用一个变量的分布与这个变量给定下另一个变量的条件分布可给出联合分布:
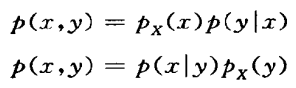
全概率公式的密度函数形式
假如能获得X的密度函数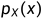 及在X给定下Y的条件密度函数
及在X给定下Y的条件密度函数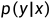 ,则由其乘积的积分可得Y的边缘分布:
,则由其乘积的积分可得Y的边缘分布:

贝叶斯公式的密度函数形式
将上面两个式子进行合并 ,可得贝叶斯公式的密度函数形式如下,贝叶斯公式的离散形式已在第一章中讨论:
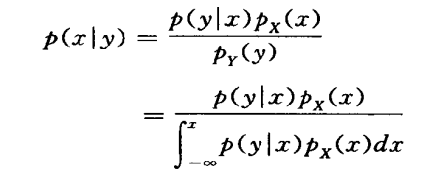
协方差
多维随机变量的数学期望与方差只利用其边缘分布所提供的信息,没有涉及诸个分量之间关系的信息。这里将提出一个新的特征数——协方差,它将能反映多维随机变量各分量间的关系。
X与Y的协方差是X的偏差与Y的偏差乘积的数学期望,定义如下:

协方差的性质:
若X与Y独立,
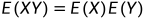 ,则
,则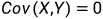
相关系数
两个随机变量之间的关系可分为独立和相依(即不独立),在相依中又可分为线性相依和非线性相依,由于非线性相依种类繁多,至今尚无实用指标来区分他们,但线性相依度可用线性相关系数来刻划,这一段将研究刻划两个变量之间线性相关程度的特征数:相关系数。
定义如下:
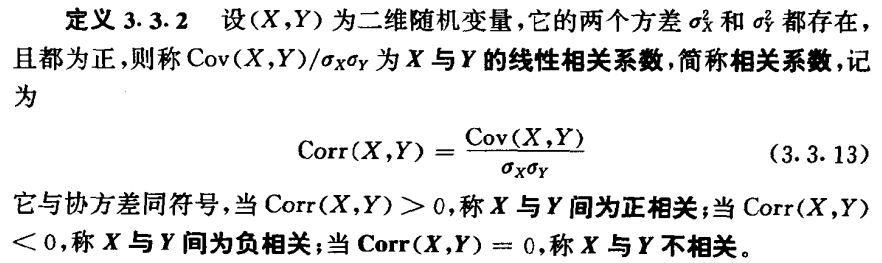
变量独立性的判别
“独立”与“不相关”
两个随机变量间的独立与不相关是两个不同概念。“相关”是指线性相关,“不相关”只说明两个随机变量之间没有线性关系,而“独立”说明两个随机变量之间既无线性关系,也无非线性关系,所以“独立”必导致“不相关”,反之不然。
变量独立性判别
其实遵从的是最简单的条件,以下条件任意一条即可(参考):
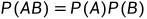 满足此即可判定AB相互独立,反映在CDF上,其实就是两个函数的每个点相乘等于其联合分布的对应点而已,宏观看起来,无非就是两个函数相乘等于概率密度函数,也就是:
满足此即可判定AB相互独立,反映在CDF上,其实就是两个函数的每个点相乘等于其联合分布的对应点而已,宏观看起来,无非就是两个函数相乘等于概率密度函数,也就是:
相应的,pdf可以判定,cdf也可以判定,因为积分操作是线性的:
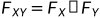
与其他变量的联合分布的边缘密度等于自己的概率密度,则相互独立。其对应条件概率
 条件,反映在连续性变量中,就是
条件,反映在连续性变量中,就是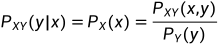
随机变量的矩

容易看出,一阶原点矩就是数学期望,二阶中心矩就是方差。
特别低,样本的高阶矩定义如下:
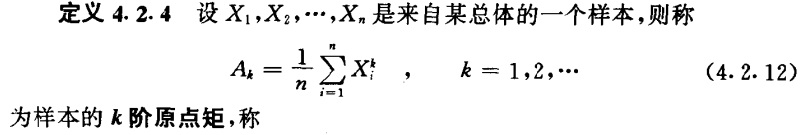

样本的方差与标准差:

第五章:参数估计
参数估计问题:参数估计中所讨论的参数不仅仅指总体分布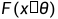 中所含的参数θ,还包括分布的各种特征数(均值、方差、标准差等),精确的确定这些参数是困难的,我们只能通过样本提供的信息对它们作出某种估计,这就是参数估计问题。
中所含的参数θ,还包括分布的各种特征数(均值、方差、标准差等),精确的确定这些参数是困难的,我们只能通过样本提供的信息对它们作出某种估计,这就是参数估计问题。
参数估计就是根据样本统计量的数值对总体参数进行估计的过程。
θ是总体的一个待估参数,其一切可能取值构成的参数空间记为  。
。
参数估计的形式有两种:点估计与区间估计。点估计是估计出一个分布中未知参数的值,区间估计则是估计出一个分布中未知参数所在的范围。
点估计
参数的点估计,是要构造一个统计量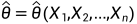 ,然后使用
,然后使用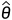 去估计θ,称
去估计θ,称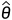 为θ的点估计或估计量,或简称估计。将样本观测值带入后便得到了θ的一个点估计值
为θ的点估计或估计量,或简称估计。将样本观测值带入后便得到了θ的一个点估计值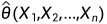
矩法估计
矩法估计的核心就是:用样本矩估计总体矩,用样本矩的相应函数估计总体矩的函数。(就是先用总体矩去构造一个表达所求参数θ的函数,然后用样本矩估计(代替)总体矩,计算参数θ)
具体的方法就是:通过计算样本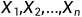 的矩,来充当分布X的矩,从而估计出总体分布X的参数θ。流程如下:
的矩,来充当分布X的矩,从而估计出总体分布X的参数θ。流程如下:

计算例子如下:
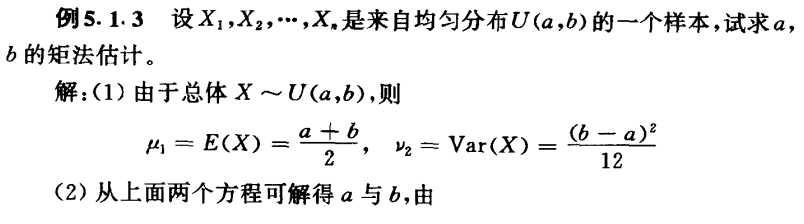
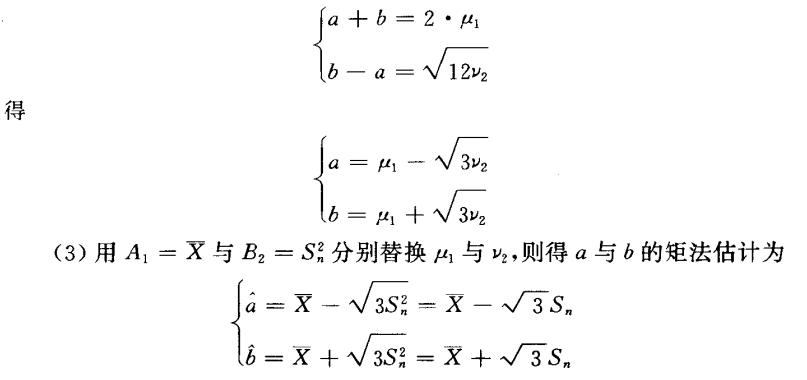
矩法估计的优点是计算简单,且在总体分布未知场合也可使用。它的缺点是不唯一,譬如泊松分布 P(λ),由于其均值和方差都是λ,因而可以用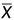 去估计λ,也可以用
去估计λ,也可以用 去估计λ;此外样本各阶矩的观测值受异常值影响较大,从而不够稳健。
去估计λ;此外样本各阶矩的观测值受异常值影响较大,从而不够稳健。
点估计的评价标准
参数的点估计实质上是构造一个估计量去估计未知参数,上节讲的矩法估计是用各种矩去构造估计量的一种方法。自然也可以用其他估计量去估计,为此就需要有评价估计好坏的准则。
无偏性
我们希望所得的估计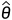 从平均意义上来讲与θ越接近越好,当其差值为0时便产生了无偏估计的概念:
从平均意义上来讲与θ越接近越好,当其差值为0时便产生了无偏估计的概念:
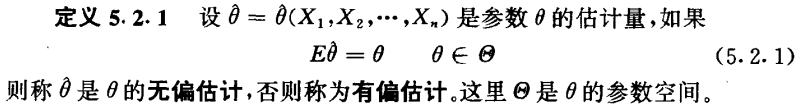
对于θ的两个无偏估计,可以通过比较他们的方差来判断哪个更好,但对于有偏估计而言,比较方差意义不大,我们关心的是估计值围绕其真值波动的大小,因而引入均方误差准则:

即当估计是有偏估计时,用MSE来进行比较。
// TODO: 无偏估计这一块不是很明白
极大似然估计
概念
极大似然估计的思想:设总体含有待估参数θ,它可以取很多值,我们要在θ的一切可能取值之中选出一个使样本观测值(已经确定)出现的概率为最大的θ值(记为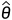 )作为θ的估计,并称
)作为θ的估计,并称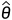 为θ的极大似然估计。极大似然估计常用
为θ的极大似然估计。极大似然估计常用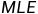 (Maximum Likelihood Estimation)表示。
(Maximum Likelihood Estimation)表示。
直白来讲,极大似然估计就是使得目前观测值出现概率最大的θ值。其基本思想是在给定数据的情况下,通过最大化似然函数来估计概率分布或模型参数。
具体来说:对于给定的观测数据集合,假设这些数据来自于一个未知的概率分布或模型,MLE方法的目标是找到最优的模型参数,使得这个模型产生这些数据的概率最大。换句话说,就是寻找一个参数估计值,使得该参数下的观测数据出现的概率最大。
下面有个例子很好的对其进行解释:

// 当随机变量是独立时,其联合概率为各自概率相乘
下面以连续分布的情况为例,给出极大似然估计的定义:

求极大似然估计的方法
寻求分布中位置参数θ的极大似然估计,首先要写出似然函数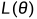 ,即样本
,即样本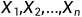 的联合分布;其次,要建立一个新的观点,让θ变换,这是同一组样本的观察值
的联合分布;其次,要建立一个新的观点,让θ变换,这是同一组样本的观察值 出现的概率
出现的概率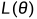 将随着θ的改变而改变。求θ的极大似然估计,就是求使
将随着θ的改变而改变。求θ的极大似然估计,就是求使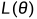 达到最大的点
达到最大的点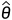 。
。
1)可以通过求导获得极大似然估计
当似然函数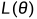 关于参数θ可导时,常常通过求导方法来获得似然函数
关于参数θ可导时,常常通过求导方法来获得似然函数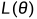 极大值对应的参数值θ。
极大值对应的参数值θ。
为求导方便,常对似然函数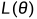 取对数,称
取对数,称 为对数似然函数,它与
为对数似然函数,它与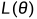 在同一点上达到最大。当
在同一点上达到最大。当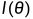 对θ的每一分量可微时,可通过
对θ的每一分量可微时,可通过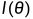 对θ的每一分量求偏导并令其为0求得极大似然估计
对θ的每一分量求偏导并令其为0求得极大似然估计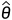 。称:
。称: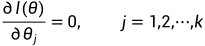 为似然方程,其中k是θ的维数。
为似然方程,其中k是θ的维数。
2)从定义出发直接求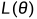 的极值点
的极值点
当似然函数的非零区域与未知参数有关时,通常无法通过解似然方程来获得参数的极大似然估计,这时可从定义出发直接求 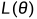 的极大值点。
的极大值点。
极大似然估计的性质
1)极大似然估计的不变原则

2)极大似然估计的渐近正态性
当样本量趋向于无穷大时,极大似然估计的分布接近于正态分布。这个结论是统计学中极为重要的一种性质,它可以用于构造置信区间和假设检验等。
具体来说,假设我们有一个来自某个分布的随机样本,样本量为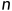 ,用
,用 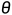 表示该分布的参数。假设我们想要使用极大似然估计
表示该分布的参数。假设我们想要使用极大似然估计 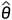 来估计参数
来估计参数 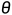 ,那么当样本量趋向于无穷大时,
,那么当样本量趋向于无穷大时,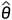 的分布会趋向于正态分布,其均值为
的分布会趋向于正态分布,其均值为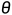 ,方差为
,方差为 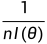 ,其中
,其中 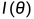 是 Fisher 信息矩阵在参数
是 Fisher 信息矩阵在参数 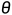 处的值。
处的值。
换句话说,如果我们有一个足够大的样本,那么我们可以使用极大似然估计来构造置信区间,置信区间的中心值是极大似然估计,置信区间的宽度则是标准误差的倍数,其中标准误差是 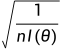 。
。
需要注意的是,这个结论只在一定条件下成立,例如样本必须是独立同分布的,并且极大似然估计的方差不能为零。此外,这个结论只是一个渐近结果,也就是说只有当样本量趋向于无穷大时才成立,对于小样本可能并不适用。
区间估计
点估计虽能给出参数一个明确的数值,但是不能提供估计参数的估计误差大小(精度),点估计主要为许多定性研究提供一定的参考数据,或在对总体参数要求不精确时使用,而在需要用精确总体参数的数据进行决策时则很少使用。
置信区间是用来估计总体参数θ真实值的一个区间,其定义如下:

对于置信区间的理解,可以参考马同学的回答:https://www.zhihu.com/question/26419030?sort=created。对于置信区间,有以下需要强调:
置信区间要求估计量是个常数
置信区间是随机区间,总体的参数是固定的,变的是不同的观测样本计算出的置信区间。比如95%的置信区间,表示在1000次抽样中,计算得到的1000个置信区间,约有950个包含正确的参数。
正态分布的区间估计
在区间估计中,当总体为正态分布时,常见的区间估计场景有以下几种:
方差已知,估计均值
方差未知,估计均值
均值未知,估计方差
总体思路就是根据正态分布的性质转化为标准正态分布,根据分为点求解区间即可。
非正态分布的区间估计
对于非正态分布,可以使用中心极限定理,近似地使用上述结果
中心极限定理:设从任意一个总体中抽取样本量为N的样本,当N充分大时,样本均值的分布近似服从于正态分布。
贝叶斯估计
统计学中有两大学派:频率学派(又称经典学派)和贝叶斯学派,它们的理论与方法都建立在概率论基础上。
以上的统计推断(点估计、区间估计)中,皆用到了两种信息:
(1) 总体信息,即总体分布或总体所属分布族给我们的信息。
(2) 样本信息,即样本提供给我们的信息。这是最“新鲜”的信息,并且越多越好,希望通过样本对总体或总体的某些特征作出较精确的统计推断。没有样本就没有统计学可言。
基于总体、样本这两种信息进行统计推断的统计学就称为经典统计学。然而在我们周围还存在着第三种信息——先验信息,它也可用于统计推断。先验信息,即在抽样之前有关统计问题的一些信息。对先验信息进行加工获得的分布称为先验分布。
基于总体、样本、先验这三种信息进行统计推断的统计学称为贝叶斯统计学。贝叶斯统计学与经典统计学的差别就在于是否利用先验信息。贝叶斯统计在重视使用总体信息和样本信息的同时,还注意先验信息的收集、挖掘和加工,使它数量化,形成先验分布,参加到统计推断中来,以提高统计推断的质量。
贝叶斯统计起源于英国学者贝叶斯(Bayes,T.R. 1702(?)-1761)死后发表的一篇论文“论有关机遇问题的求解”,在此文中提出了著名的贝叶斯公式和一种归纳推理的方法, 之后, 被一些统计学家发展成一种系统的统计推断方法。到上世纪30年代已形成贝叶斯学派,到50~60年代已发展成一个有影响的统计学派,其影响还在日益扩大。
贝叶斯学派的最基本的观点是:任一未知量θ都可看作随机变量,可用一个概率分布去描述,这个分布称为先验分布。因为任一未知量都有不确定性,而在表述不确定性的程度时,概率与概率分布是最好的语言。
如今两派的争论焦点已从“未知量是否可看作随机变量”转换为“如何利用各种先验信息合理地确定先验分布”。
两个学派的区别如下:(参考:贝叶斯学派与频率学派有何不同?)
频率派把模型参数看成未知的常量,用极大似然法MLE(一种参数点估计方法)求解参数,往往最后变成最优化问题。这一分支又被称为统计学习。频率派认为概率是事物的固有属性,是一个确定的常量,它就在那里,只是我们暂时不知道而已,要估计出这个确定的概率,可以做重复实验并计算重复实验中事件发生的频率,用频率近似概率(依据是“大数定律”),样本量越大,这个近似就越好。
贝叶斯派把模型参数看成未知的变量(概率分布),用最大化后验概率MAP求解参数。贝叶斯派认为总体的未知参数是一个随机变量,它有自己的分布,把它叫做“先验分布”。贝叶斯学派就是利用先验分布和贝叶斯公式来得到后验分布,然后基于后验分布做进一步的统计推断。
相关文章:

概率论与数理统计相关知识
本博客为《概率论与数理统计--茆诗松(第二版)》阅读笔记,目的是查漏补缺前置知识数学符号连乘符号:;总和符号:;“任意”符号:∀;“存在”符号&…...

SOC计算方法:卡尔曼滤波算法
卡尔曼滤波算法是一种经典的状态估计算法,它广泛应用于控制领域和信号处理领域。在电动汽车领域中,卡尔曼滤波算法也被广泛应用于电池管理系统中的电池状态估计。其中,电池的状态包括电池的剩余容量(SOC)、内阻、温度等…...

【C语言】自定义类型、枚举类型与宏定义
目录一、自定义类型二、宏定义三、枚举类型一、自定义类型 自定义类型关键字:typedef,用新的类型名称代替原有的类型名。 例如: typedef char u8; u8 x;表示指定u8为新的类型名,代替char,作用与char相同,…...

Java进阶(下篇2)
Java进阶(下篇2)一、IO流01.File类的使用1.1、File类的实例化1.2、File类的常用方法11.3、File类的常用方法21.4、课后练习02、IO流原理及流的分类2.1、IO流原理2.2、流的分类2.3、IO 流体系03、节点流(或文件流)3.1、FileReader读入数据的基本操作3.2、…...

03单链表
、# 单链表 单链表是一种链式存储的数据结构,用一组地址任意的存储单元存放线性表中的数据元素。单链表中的每个结点包含一个数据域和一个指针域,数据域存放数据元素,指针域存放下一个结点的地址。单链表的第一个结点称为头结点,…...
ESLint、Prettier插件的安装与使用
在统一代码风格这一块,通常大家都会用到ESLint。虽然 ESLint 本身具备自动格式化代码的功能,但ESLint 的主要优势在于代码的风格检查并给出提示,而在代码格式化这一块 Prettier 做的更加专业,因此在实际项目开发中我们经常将 ESLi…...

matlab在管理学中的应用简matlab基础【三】
规划论及MATLAB计算 1、线性规划 问题的提出 例1. 某工厂在计划期内要安排甲、乙两种产品的生产,已知生产单位产品所需的资源A、B、C的消耗以及资源的计划期供给量,如下表: 问题:工厂应分别生产多少单位甲、乙产品才能使工厂获…...
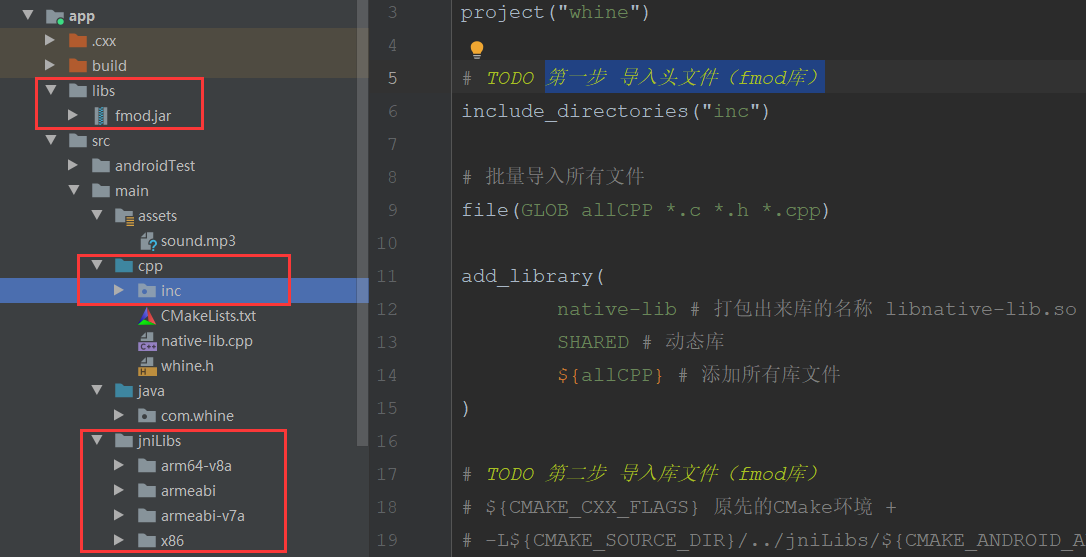
NDK JNI 变声器实现
Android NDK 导入 C库的开发流程学习;通过使用fmod的C库,实现变声器功能。导入库文件1)复制fmod的C库到cpp目录下2)复制fmod的so库到jniLibs目录下3)复制fmod的jar库到libs目录下4)将声音文件复制到assets目…...

VMLogin防关联指纹浏览器的主帐号和子账号区别介绍
VMLogin主账户管理子账户,主要用于团队协作,分账户登录使用,主账户相当于老板,子账户相当于员工。 主账户创建并管理子账户; 主账户可以修改子账户的密码; 主账户可以设置子账户是否有创建配置文件权限&a…...

Apache DolphinScheduler GitHub Star 突破 10000!
点击蓝字 关注我们今天,Apache DolphinScheduler GitHub Star 突破 10000,项目迎来一个重要里程碑。这表明 Apache DolphinScheduler 已经在全球的开发者和用户中获得了广泛的认可和使用。DolphinScheduler 旨在解决公司日常运营中的大数据处理工作流调度…...

程序员中的女性力量——做不被定义的自己
她是office lady,亦是程序媛,程序员界的靓丽色彩,不可或缺。 “只有那些疯狂到以为自己能够改变世界的人——才能真正改变世界。” 女性该如何定义自己?程序媛怎么发挥自己最大的价值。 争取自己做选择,经济和思想都独…...

pb中Datawindow中每页打印固定行
Datawindow中每页打印固定行 第一步: 增加一个计算列,此计算列必须放在Detail段,Expression中输入:ceiling(getrow()/20),这里20还可以用全局函数取代,这样可以允许用户任意设置每页打印多少行。 第二步: 定义分组,选择菜单Rows->Create Group...按计算列字段…...
【独家】)
华为OD机试 - 内存池(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:内存池题…...

SaaS简介
SaaS 简介 SaaS被认为是云计算的一部分,其他包括基础设施即服务(IaaS)、平台即服务(PaaS)、桌面即服务(DaaS)、托管软件即服务(MSaaS)、移动后端即服务(MBaaS)、数据中心即服务(DCaaS)、集成平台即服务(iPaaS)和信息技术管理即服务(ITMaaS) SaaS应用程序通常由web浏…...

unity 实现使用三张图片来表达车速,通过传值达到车速
//速度 public Image SpeedNums_Unit; public Image SpeedNums_Ten; //public Image SpeedNums_Hundred; //kw public Image MileageNums_Unit; public Image MileageNums_Ten; /// /// 仪表速度UI /// private void SpeedUI(string speedStr) {if (SpeedNums_Unit == null) …...
程序员看过都说好的资源网站,你值得拥有。
程序员必备的相关资源网站一.技术社区1.GitHub2.Gitee(码云)3.稀土掘金4.OSCHINA开源中国5.CSDN6.博客园7.SegmentFault(思否)8.Stack Overflow9.Golang中文社区10.ChinaUnix11.51CTO12.Ruby China二.技术教程1.Devdocs2.码农教程…...

【MySQL高级篇】第03章 用户与权限管理
第03章 用户与权限管理 1. 用户管理 1.1 登录MySQL服务器 启动MySQL服务后,可以通过mysql命令来登录MySQL服务器,命令如下: mysql –h hostname|hostIP –P port –u username –p DatabaseName –e "SQL语句"-h参数后面接主机…...
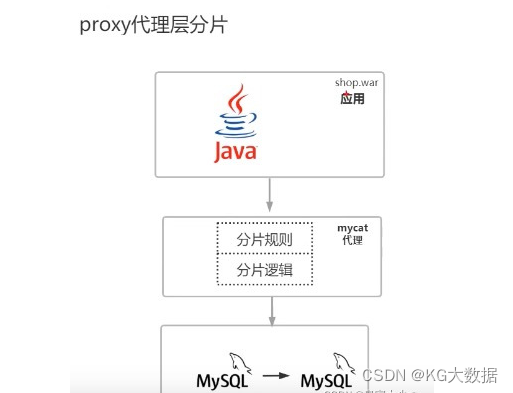
MySQL的分库分表?通俗易懂
1- 为什么要分库分表 如果一个网站业务快速发展,那这个网站流量也会增加,数据的压力也会随之而来,比如电商系统来说双十一大促对订单数据压力很大,Tps十几万并发量,如果传统的架构(一主多从)&a…...

elasticsearch 查询语法
match_all 查询所有 GET test/_search {"query": {"match_all": {}} }match 单字段匹配查询 GET test/_search {"query":{"match":{"name":"zhangsan"}} }multi_match 多字段匹配查询 GET test/_search {"…...

深入剖析MVC模型与三层架构
MVC(Model-View-Controller)模型和三层架构都是常见的软件架构模式,用于实现大型应用程序和软件系统。下面是对它们的深入剖析: MVC模型 MVC模型是一种将应用程序分成三个主要组件的软件架构模式,分别是模型…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

大数据零基础学习day1之环境准备和大数据初步理解
学习大数据会使用到多台Linux服务器。 一、环境准备 1、VMware 基于VMware构建Linux虚拟机 是大数据从业者或者IT从业者的必备技能之一也是成本低廉的方案 所以VMware虚拟机方案是必须要学习的。 (1)设置网关 打开VMware虚拟机,点击编辑…...

高频面试之3Zookeeper
高频面试之3Zookeeper 文章目录 高频面试之3Zookeeper3.1 常用命令3.2 选举机制3.3 Zookeeper符合法则中哪两个?3.4 Zookeeper脑裂3.5 Zookeeper用来干嘛了 3.1 常用命令 ls、get、create、delete、deleteall3.2 选举机制 半数机制(过半机制࿰…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据
微软PowerBI考试 PL300-在 Power BI 中清理、转换和加载数据 Power Query 具有大量专门帮助您清理和准备数据以供分析的功能。 您将了解如何简化复杂模型、更改数据类型、重命名对象和透视数据。 您还将了解如何分析列,以便知晓哪些列包含有价值的数据,…...

使用Matplotlib创建炫酷的3D散点图:数据可视化的新维度
文章目录 基础实现代码代码解析进阶技巧1. 自定义点的大小和颜色2. 添加图例和样式美化3. 真实数据应用示例实用技巧与注意事项完整示例(带样式)应用场景在数据科学和可视化领域,三维图形能为我们提供更丰富的数据洞察。本文将手把手教你如何使用Python的Matplotlib库创建引…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...