还是要学好数学啊
有一个无穷大的二维网格图,一开始所有格子都未染色。给你一个正整数 n ,表示你需要执行以下步骤 n 分钟:
第一分钟,将任一格子染成蓝色。
之后的每一分钟,将与蓝色格子相邻的 所有 未染色格子染成蓝色。
下图分别是 1、2、3 分钟后的网格图。

请你返回 n 分钟之后 被染色的格子 数目。
题目链接:https://leetcode.cn/problems/count-total-number-of-colored-cells
今天刷到这题,觉得有意思。在纸上画的麻烦,搞个excel涂色,还挺减压的,就像这样:

n=1时,红色1
n=2时,多了橙色,1 + 4 = 5
n=3时,多了绿色,5 + 8 = 13
n=4时,多了紫色,13 + 12 = 25
观察下,规律来了:
n=1时,红色1 = 1 + (1 - 1)* 4
n=2时,多了橙色,1 + 4 = 5 = 1 + (2 - 1)* 4
n=3时,多了绿色,5 + 8 = 13 = 5 + (3 - 1)* 4
n=4时,多了紫色,13 + 12 = 25 = 13 + (4 - 1)* 4
那么公式,就是: 后一个数 = 前一个数 + (n-1)*4
这让人联想到类似斐波拉契数组的解法,F(n) = F(n-1) + (n-1) * 4
于是代码如下,可见非常低效 ,因为太多重复计算了。
,因为太多重复计算了。

既然都知道公式了,可以把公式用作 DP 动态规划转移方程,可以将粗暴递归的重复计算变成线性的 O(n) 规模。
于是代码如下:
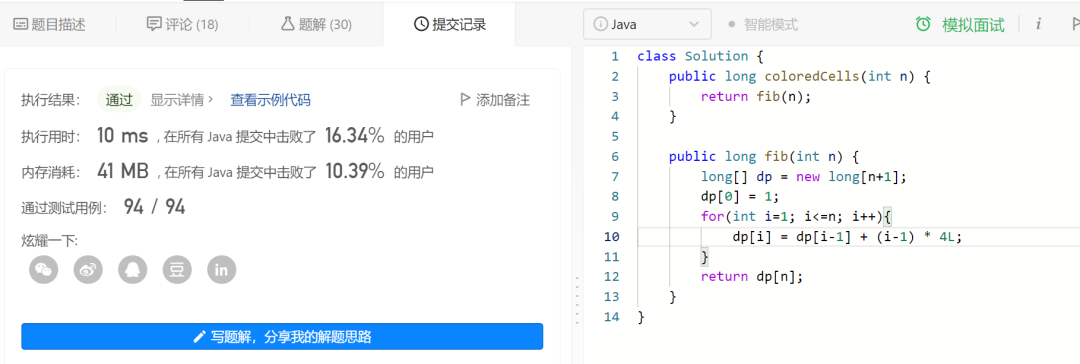
有一点点提升
发大招,上数学归纳法

这是我家女神帮我算的,我这学渣不懂,说是什么高斯定理,高斯是谁?大家知道吗?
(什么?字不好看?风大听不见,你再说一遍?哦哦,没关系,人漂亮啊)
管他呢,现在有了公式,代码就只要一行了,秀的简直不行不行的。
感受下,击败100%
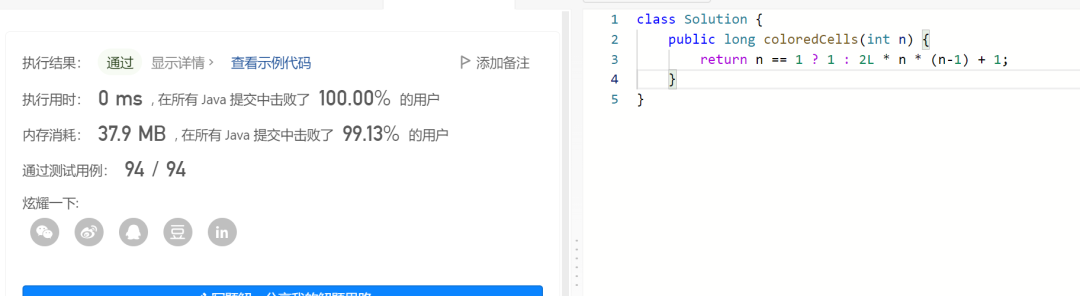
数学好,就是秒杀全场,什么迭代,什么动态规划,都不在话下。
所以,同学们,弟弟妹妹们,还是好好学数学吧。
当然,还有一个 excel 图像法,我不会推公式,我会画图,小学数学老师教的 “加辅助线” ,加辅助线也能推导出用高斯推导出来的那个啥公式,你看看。
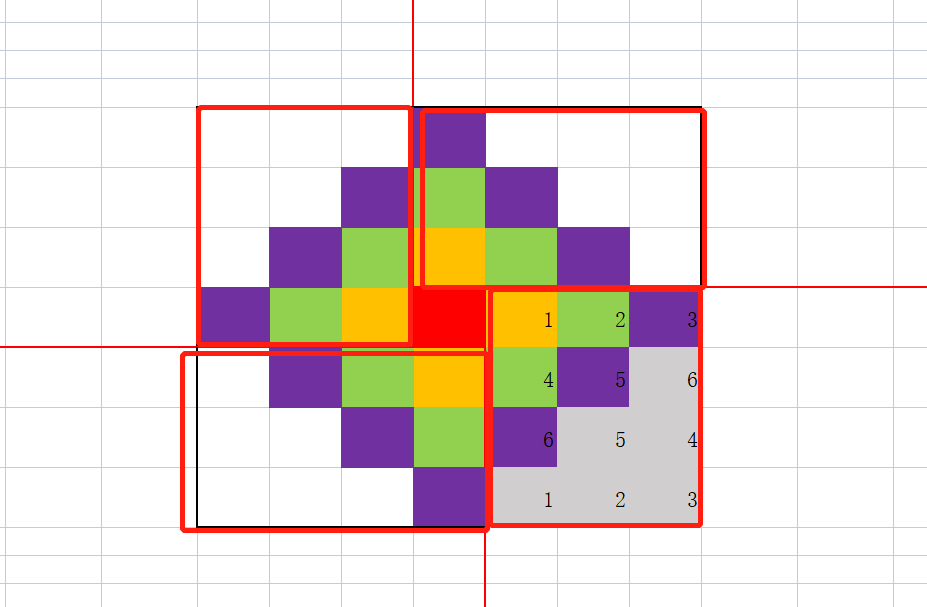
四条红色的辅助线,把图像分成了四个大红块,加中间一个小红块
中间一个小红块就是1
大红块的规律,看右下角,标了数字,好数。
这是 n = 4 时候的图,长方形的面积等于长乘以宽,4乘以3,然后去掉灰色的恰好是一半,4*3/2,那么得到公式就是(n-1)乘以 n 乘积的一半。
那么最终的公式就是:
F(n) = 4 个大红块面积的一半 + 1 个小红块
= 两个大红块面积 + 1个小红块
= 2 * n *(n-1) + 1
所以,图形化的学数学,简直太棒了。(这点建议希望数学老师参考下哈,不然学得没有趣味,还会有很多我这样的学渣 

 )
)
相关文章:

还是要学好数学啊
有一个无穷大的二维网格图,一开始所有格子都未染色。给你一个正整数 n ,表示你需要执行以下步骤 n 分钟:第一分钟,将任一格子染成蓝色。之后的每一分钟,将与蓝色格子相邻的 所有 未染色格子染成蓝色。下图分别是 1、2、…...
ActiveMQ反序列化漏洞原理+复现
ActiveMQ反序列化漏洞 ActiveMQ ActiveMQ是开源消息总线,消息中间件 工作原理 通过使用消息队列,实现服务的异步处理,主要目的是减少请求响应时间和解耦合。 消息队列,服务器A将客户发起的请求放入服务器B的消息队列中&#…...
layui框架实战案例(19):layui-table模块表格综合应用(筛选查询、导入导出、群发短信、一键审核、照片展示、隐私加密)
系列文章目录 layui动态表格翻页和搜索的代码分析layui框架实战案例(3):layui上传错误请求上传接口出现异常解决方案layui框架实战案例(9):layPage 静态数据分页组件layui框架实战案例(10):短信验证码60秒倒计时layui框架实战案例(11)&#…...

分析vmlinux,uImage,zImage,Image的生成以及之间的关系
1.在内核源码顶层目录下打开Makefile,搜索vmlinux,找到以下内容:可知主要靠$(vmlinux-deps)生成。继续搜索查看变量vmlinux-deps的值,找到:KBUILD_LDS为链接文件,剩下两个变量如下:搜索head-y未…...
)
设计模式-六大设计原则详解(java 版)
设计模式-六大设计原则单一职责原则里氏替换原则开闭原则接口隔离原则依赖倒置原则迪米特法则初次接触设计模式是在就读大学期间,或许那时候进入实验室有较好的导师及厉害点的同学,接的校外的商业代码都较为规范整洁,拗口的设计模式在学习中便…...

Linux下Nginx安装使用
一、下载解压nginx # 进入要放安装包的目录 cd /opt/software # 下载安装包 wget https://nginx.org/download/nginx-1.20.2.tar.gz # 解压缩 tar -zxvf nginx-1.20.2.tar.gz -C /opt/modules # 进入解压后的目录 cd /opt/modules/nginx-1.20.2/二、安装nginx 1、安装编译器 …...

推动汽车业务向前发展的混合云战略:汽车数据解决方案
推动汽车业务向前发展的混合云战略 无论您的数据是位于内部还是公有云中,与 NetApp 合作都可以帮助您的汽车业务充分发挥它们的潜能 前有混合动力汽车,后有混合云 通过精心考虑的混合多云战略,汽车制造商可以根据不同需求和环境移动应用程序…...

Boosting三巨头:XGBoost、LightGBM和CatBoost(发展、原理、区别和联系,附代码和案例)
❤️觉得内容不错的话,欢迎点赞收藏加关注😊😊😊,后续会继续输入更多优质内容❤️👉有问题欢迎大家加关注私戳或者评论(包括但不限于NLP算法相关,linux学习相关,读研读博…...
-10)
设计模式~模板方法模式(Template method)-10
目录 (1)优点: (2)缺点: (3)使用场景: (4)注意事项: (5)应用实例: (6)Servlet Api & Spring 中的应用 代码 (钩子函数)在模板模式(Template Pattern)中,一个抽象类公开定…...

【WebSocket】在SSM项目中配置websocket
在SSM项目中配置websocket 最近在ssm项目中配置了websocket,踩了很多坑,来分享一下 本文暂不提供发送消息等内容的代码逻辑(后续也许会补充),如果你直接复制这类可能会对配置造成更大的麻烦(博主就是复制…...

node-red中创建自定义节点 JavaScript 文件API编写详解
前言 在node-red中如果你没有找到自己需要的节点时,那么你可以自定义一个节点来满足自己的需求。之前的文章中,我有简单介绍过如何创建一个节点,并以转换大小写来举例。例子虽然简单,但可以让大家了解创建自定义节点的步骤以及一个节点的组成部分。那么本篇将会聚焦在自定…...
【独家】)
华为OD机试 - 寻找路径 or 数组二叉树(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:寻找路径…...

YOLOv7、YOLOv5改进之打印热力图可视化:适用于自定义模型,丰富实验数据
💡该教程为改进YOLO高阶指南,属于《芒果书》📚系列,包含大量的原创改进方式🚀 💡更多改进内容📚可以点击查看:YOLOv5改进、YOLOv7改进、YOLOv8改进、YOLOX改进原创目录 | 唐宇迪老师联袂推荐🏆 💡🚀🚀🚀内含改进源代码 按步骤操作运行改进后的代码即可�…...

【Java代码与架构之完美优化】篇1:代码质量优化通用准则
工欲善其事,必先利其器 1. 避免使用空块 常见空块一般有以下几种情况: 多余的分号:if(xxx);多余的大括号:if(xxx){这里没有内容}空finall语句:try{...}catch(...){...}finally{这里没有内容} 空块的存在࿰…...

Linux进程间通信详解(最全)
进程间的五种通信方式介绍 进程间通信(IPC,InterProcess Communication)是指在不同进程之间传播或交换信息。IPC的方式通常有管道(包括无名管道和命名管道)、消息队列、信号量、共享内存、Socket(套接字&a…...

ROS 摄像头的使用
参考: youtubeArticulated Robotics 作者Josh Newans博客 建议: 这个只是我的看法,强烈建议看原视频或博客 png:无损压缩 jpeg:有损压缩 Driver Node 负责连接硬件设备,读取摄像头数据"ima…...

VR全景云展厅,实现7*24小时的线上宣传能力!
数字化时代,虚拟现实技术的应用越来越广泛,其中VR全景云展厅是一种新兴的展示方式,具有独特的展示优势。随着VR技术的不断发展,越来越多的企业、机构和个人开始使用VR全景云展厅来展示他们的产品和服务。一、展厅营销痛点1、实地到…...
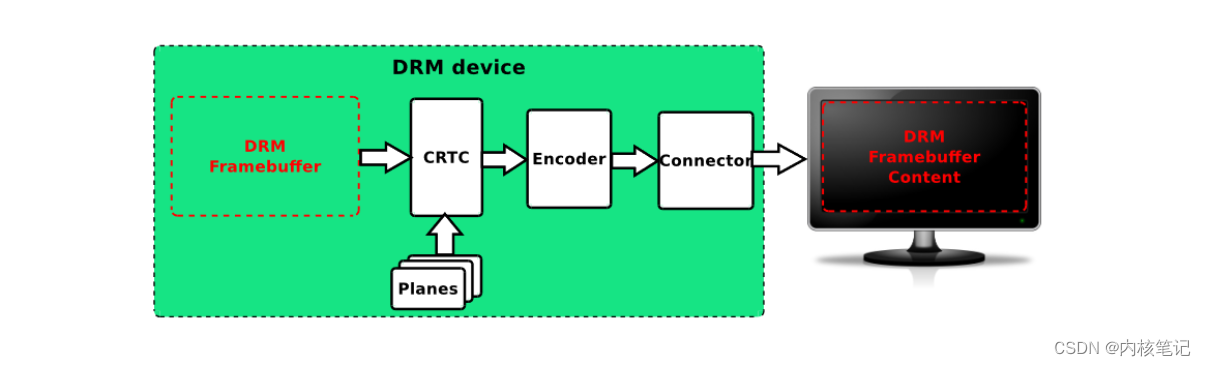
RK3568平台开发系列讲解(显示篇) DRM显示系统组成分析
🚀返回专栏总目录 文章目录 一、DRM Framebuffer二、CRTC三、Planes四、Encoder五、Connector沉淀、分享、成长,让自己和他人都能有所收获!😄 📢让我们分析一下绿框中的五个部件,以及他们的联动。 一、DRM Framebuffer 与 framebuffer一样,是一片存放图像的内存区域,…...
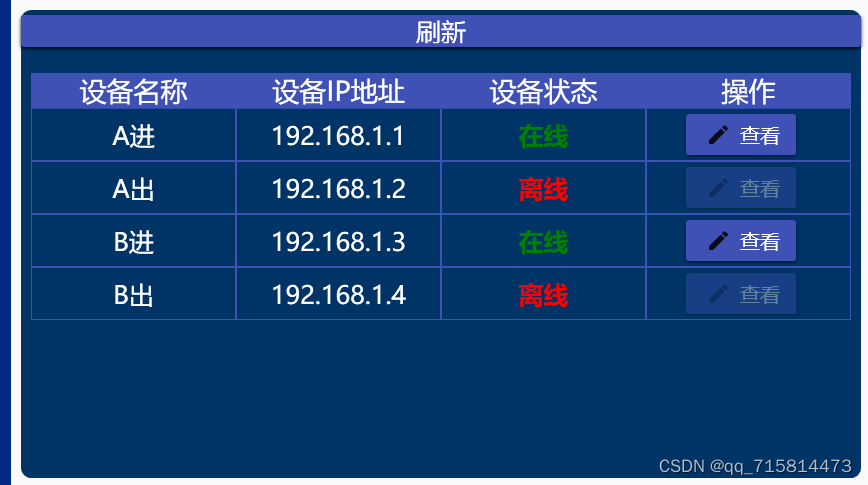
WPF DataGrid控件的使用 使用列模板来进行数据格式的美化
<Grid><Grid.RowDefinitions><RowDefinition Height"0.1*" /><RowDefinition /></Grid.RowDefinitions><Button Content"刷新"FontSize"25"Command"{Binding ExecuteRefreshCommand}" /><Dat…...
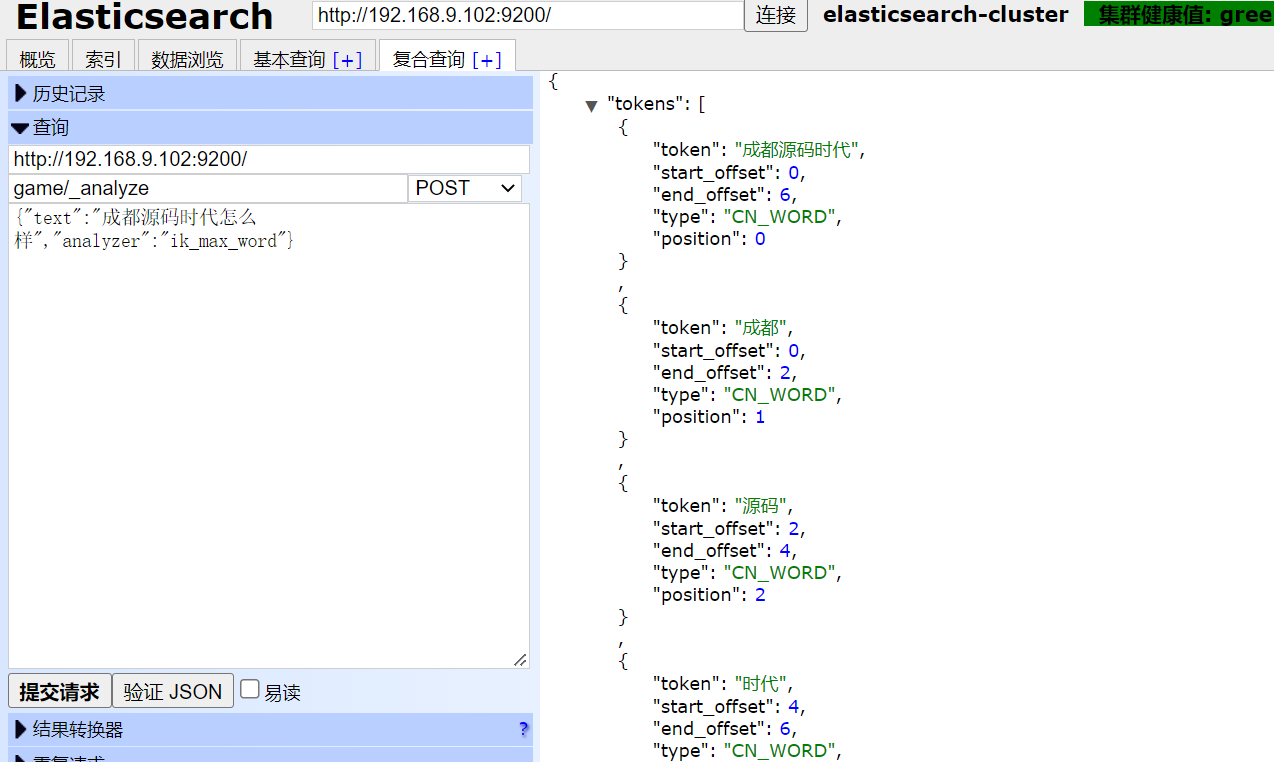
elasticsearch自定义企业词典
我们中文分词用的是ik,但是ik只是对基本的中文词进行了分词,而对于企业或者人名没有进行分词。比如,我搜索中国平安,那么ik只能分成中国、平安如果这样,这肯定是不行滴!接下来,俺就教你…...
)
Java 语言特性(面试系列1)
一、面向对象编程 1. 封装(Encapsulation) 定义:将数据(属性)和操作数据的方法绑定在一起,通过访问控制符(private、protected、public)隐藏内部实现细节。示例: public …...

Xshell远程连接Kali(默认 | 私钥)Note版
前言:xshell远程连接,私钥连接和常规默认连接 任务一 开启ssh服务 service ssh status //查看ssh服务状态 service ssh start //开启ssh服务 update-rc.d ssh enable //开启自启动ssh服务 任务二 修改配置文件 vi /etc/ssh/ssh_config //第一…...

相机Camera日志实例分析之二:相机Camx【专业模式开启直方图拍照】单帧流程日志详解
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了: 这一篇我们开始讲: 目录 一、场景操作步骤 二、日志基础关键字分级如下 三、场景日志如下: 一、场景操作步骤 操作步…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...
