(蓝桥真题)剪格子(搜索+剪枝)
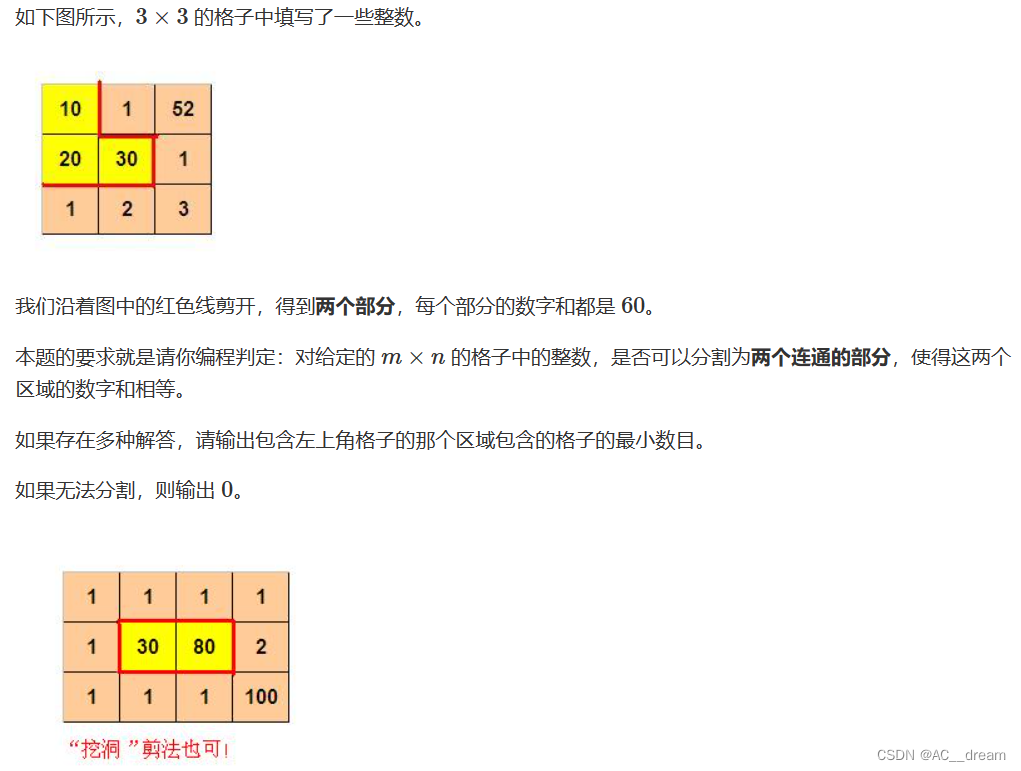

样例1输入:
3 3
10 1 52
20 30 1
1 2 3样例1输出:
3样例2输入:
4 3
1 1 1 1
1 30 80 2
1 1 1 100样例2输出:
10分析:这道题目我们直接从(1,1)点开始进行dfs搜索即可,但是需要注意一点的是我们搜索的时候并不是沿着一条路径进行搜索,而是从当前已经走过的所有点中选出一个点然后沿着不同方向去搜索,这样我们就可以搜出所有的连通块,每次搜出一个连通块时还需要检测剩余的部分是否是一个连通块,那么检测剩余部分是否是一个连通块我们可以用并查集来实现。这样大体的步骤就实现了,接下来就是剪枝了,为了防止同样的状态被多次搜索,我们可以用哈希优化一下,随意设置一个哈希函数,然后求出每个连通块对应的哈希值然后进行去重即可,还有可以优化的一点就是我们每次尽可能选取值大的点进行搜索,这样得到目标值的连通块内的点就会尽可能小。
需要说明的一点就是:由于蓝桥原题是没有明确说明两部分都必须连通的,所以也就没必要加上判断连通的那部分,而且他数据中都是一笔画形成的连通块,没有考虑周全,所以本代码在这两方面进行了优化,但会在洛谷上提交时会有一个点超时,那是因为本代码充分考虑到其余部分是否连通以及连通块形状任意这两个问题。
细节见代码:
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
#include<unordered_set>
using namespace std;
typedef pair<int,int> PII;
const int N=12;
const int P=13331;//P用于哈希
unordered_set<unsigned long long>st;
PII p[N*N];//存放当前已选的点
int a[N][N];
bool vis[N][N];
int fu[N*N],sum,ans,n,m;
int dx[4]={0,0,1,-1},dy[4]={1,-1,0,0};
bool cmp(PII x,PII y)
{return a[x.first][x.second]>a[y.first][y.second];
}
int find(int x)
{if(fu[x]!=x) return fu[x]=find(fu[x]);return x;
}
bool check_connect(int cnt)//检查剩余的n*m-cnt个点是否连通
{for(int i=1;i<=n*m;i++) fu[i]=i;int t=n*m-cnt;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)if(!vis[i][j]){for(int k=0;k<4;k++){int nx=i+dx[k],ny=j+dy[k];if(nx<1||nx>n||ny<1||ny>m) continue;if(vis[nx][ny]) continue;int fx=find((i-1)*m+j),fy=find((nx-1)*m+ny);if(fx==fy) continue;t--;fu[fx]=fy;}}return t==1;
}
bool check_exit()//检查当前连通块是否已经被搜索过,是的话返回true,否则返回false
{unsigned long long t=0; for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)if(vis[i][j])t=t*P+i*(P-3)+j*(P+102);if(st.count(t)) return true;//哈希去重st.insert(t);return false;
}
void dfs(int s,int cnt)//s和cnt分别代表当前已经选出来的数的和及个数
{if(s==sum/2){if(check_connect(cnt)) ans=min(ans,cnt);//检查其他格子是否为一个连通块 return ;}if(s>sum/2||cnt>=ans) return ;//剪枝 PII next[N*N];//存放下一次搜索的点 int t=0;for(int i=1;i<=cnt;i++){int nowx=p[i].first,nowy=p[i].second;for(int j=0;j<4;j++){int nx=nowx+dx[j],ny=nowy+dy[j];if(nx<1||nx>n||ny<1||ny>m) continue;if(vis[nx][ny]) continue;next[++t]={nx,ny};}}sort(next+1,next+t+1,cmp);for(int i=1;i<=t;i++){if(next[i]==next[i-1]) continue;p[cnt+1]=next[i];vis[next[i].first][next[i].second]=true;if(!check_exit())//检查当前连通块是否已经被搜索过dfs(s+a[next[i].first][next[i].second],cnt+1);vis[next[i].first][next[i].second]=false;}
}int main()
{cin>>m>>n;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){scanf("%d",&a[i][j]);sum+=a[i][j];}if(sum&1){printf("0");return 0;}ans=0x3f3f3f3f;vis[1][1]=true;p[1]={1,1};dfs(a[1][1],1);if(ans==0x3f3f3f3f) ans=0;printf("%d",ans);return 0;
}相关文章:

(蓝桥真题)剪格子(搜索+剪枝)
样例1输入: 3 3 10 1 52 20 30 1 1 2 3 样例1输出: 3 样例2输入: 4 3 1 1 1 1 1 30 80 2 1 1 1 100 样例2输出: 10 分析:这道题目我们直接从(1,1)点开始进行dfs搜索即可,但是需要注意一点的是我们搜…...

Kalman Filter in SLAM (3) ——Extended Kalman Filter (EKF, 扩展卡尔曼滤波)
文章目录1. 线性系统的 Kalman Filter 回顾2. Extended Kalman Filter 之 DR_CAN讲解笔记2.1. 非线性系统2.2. 非线性系统线性化2.2.1. 状态方程f(xk)f(x_k)f(xk)在上一次的最优估计状态x^k−1\hat{x}_{k-1}x^k−1处线性化2.2.2. 观测方程h(xk)h(x_k)h(xk)在这一次的预测…...

关于vertical-align的几问
vertical-align属性可以给我讲解一下吗? 当使用table-cell布局或inline元素时,可以使用CSS的vertical-align属性控制元素的垂直对齐方式。该属性可应用于元素本身以及其父元素(例如,td、th、tr和table)。 以下是vertic…...

【拜占庭将军问题】这一计谋,可以让诸葛丞相兴复汉室
我们都知道,诸葛亮第一次北伐是最可能成功的,魏国没有防备,还策反了陇西,陇西有大量的马匹可以装备蜀国骑兵,可惜街亭一丢,那边就守不住了 当时我不在,只能作诗一首~ 如果穿越过去,…...
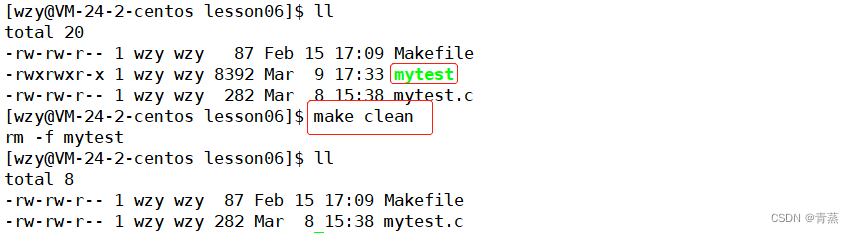
【Linux】 -- make/Makefile
目录 Linux项目自动化构建工具 – make/Makefile 背景 依赖关系和依赖方法 多文件编译 项目清理 make原理 Linux项目自动化构建工具 – make/Makefile 背景 一个工程的源文件不计其数 按照其类型、功能、模块分别放在若干个目录当中 Makefile定义了一系列的规则来指定&…...

Forter 对支付服务商应对欺诈的四个建议和Gartner的两个关键结论
Gartner新版2023年度《线上欺诈检测市场指南》发布恰逢其时-企业正面临来自专业黑产和欺诈者与日俱增的压力。而在2023年,许多商户将调整反欺诈策略,对拒付率和转化率进行更严格的监测,以最大限度减少损失并增加营收。以下是Gartn…...
——ANR监听方案之IdleHandler)
ANR系列(二)——ANR监听方案之IdleHandler
前言 关于IdleHandler,比较多同学错误地认为,这个Handler的作用是主线程空闲状态时才执行它,那么用它做一些耗时操作也没所谓。可是IdleHandler在主线程的MessageQueue中,执行queueIdle()默认当然也是执行在主线程中的࿰…...
)
数学小课堂:数学和自然科学的关系(数学方法,让自然科学变成科学体系。)
文章目录 引言I 数学方法,让自然科学变成科学体系。1.1 天文学1.2 博物学1.3 化学1.4 医药学1.5 物理学II 自然科学的升华过程III 数学方法的意义引言 19世纪初,英国人把采用实验的方法,系统地构造和组织知识,解释和预测自然的学问称为科学。 科学研究的是自然现象和自然…...

[蓝桥杯 2020 省 A1] 分配口罩
思路比较容易想到,因为口罩全部只有15批,因此直接暴力dfs搜索即可 //dfs #include<bits/stdc.h> using namespace std; int ans 9999; int num[] {9090400, 8499400, 5926800, 8547000, 4958200, 4422600, 5751200, 4175600, 6309600, 5865200, …...
第五章:C语言数据结构与算法之双向带头循环链表
系列文章目录 文章目录系列文章目录前言一、哨兵位的头节点二、双向链表的结点三、接口函数的实现1、创建结点2、初始化3、尾插与尾删4、头插与头删5、打印6、查找7、随机插入与随机删除8、判空、长度与销毁四、顺序表和链表的对比1. 不同点2. 优缺点五、缓存命中1、缓存2、缓存…...
一文带你了解,前端模块化那些事儿
文章目录前端模块化省流:chatGPT 总结一、参考资料二、发展历史1.无模块化引出的问题:横向拓展2.IIFE3.Commonjs(cjs)4.AMD引出的问题:5.CMD6.UMD7.ESM往期精彩文章前端模块化 省流:chatGPT 总结 该文章主要讲述了前端模块化的发展历史和各个…...
大白话设计索引的时候,我们一般要考虑哪些因素呢?(中))
(六十五)大白话设计索引的时候,我们一般要考虑哪些因素呢?(中)
今天我们继续来说一下,在设计索引的时候要考虑哪些因素。之前已经说了,你设计的索引最好是让你的各个where、order by和group by后面跟的字段都是联合索引的最左侧开始的部分字段,这样他们都能用上索引。 但是在设计索引的时候还得考虑其他的…...

Spring事务管理
文章目录1 事务1.1 需求1.2 原因分析1.3 错误解决1.4 yml配置文件中开启事务管理日志1 事务 1.1 需求 当部门解散了不仅需要把部门信息删除了,还需要把该部门下的员工数据也删除了。可当在删除员工数据出现异常时,就不会执行删除员工操作,出…...
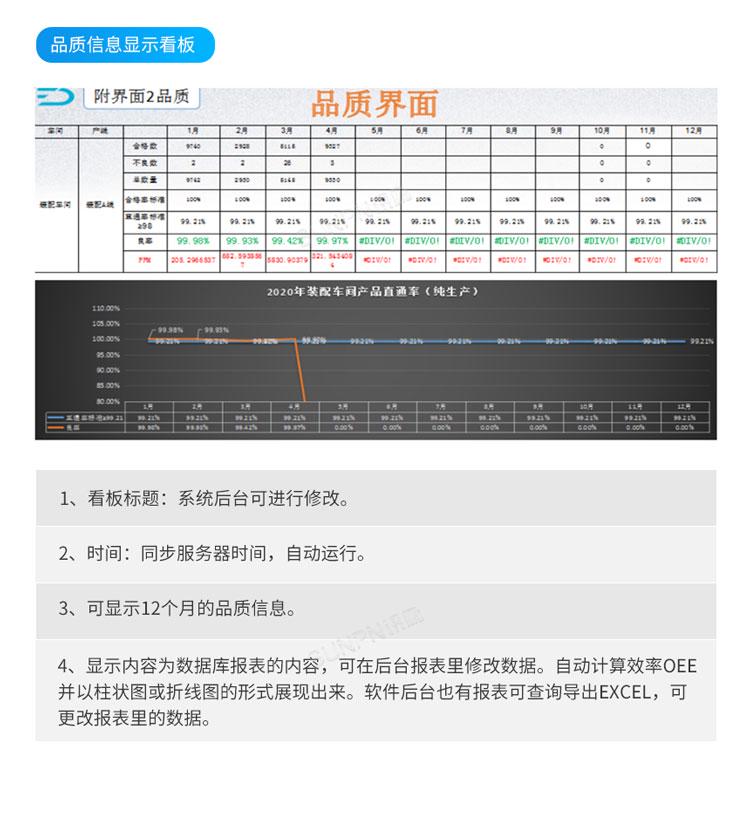
数字化工厂装配线生产管理看板系统
电力企业业务复杂,组织结构复杂,不同的业务数据,管理要求也不尽相同。生产管理看板系统针对制造企业的生产应用而开发,能够帮助企业建立一个规范准确即时的生产数据库。企业现状:1、计划不清晰:生产计划不能…...
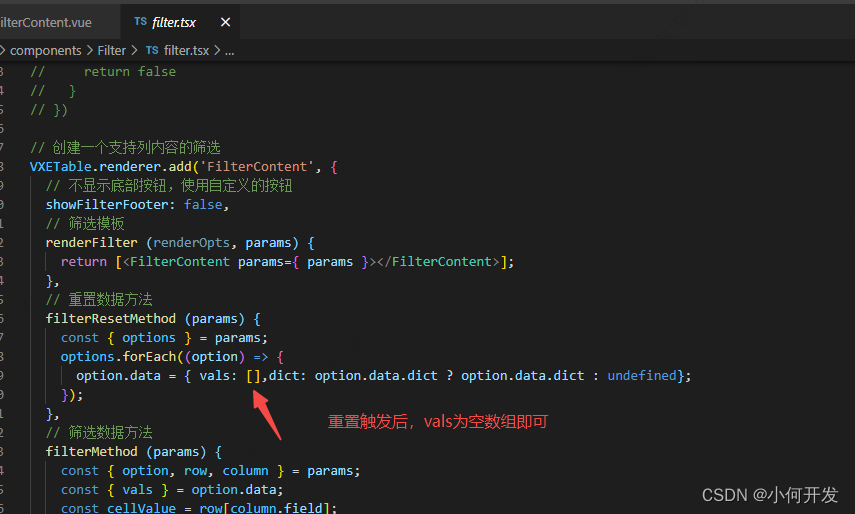
vxe-grid 全局自定义filter过滤器,支持字典过滤
一、vxe-table的全局筛选器filters的实现 官网例子:https://vxetable.cn/#/table/renderer/filter 进入之后:我们可以参照例子自行实现,也可以下载它的源码,进行调整 下载好后并解压,用vscode将解压后的文件打开。全局…...
ECharts 环形图组件封装
一、ECharts引入1.安装echarts包npm install echarts --save2.引入echarts这里就演示全局引入了,挂载到vue全局,后面使用时,直接使用 $echartsimport * as echarts from echarts Vue.prototype.$echarts echarts二、写echarts组件这里演示环…...

c++ 怎么调用python 提供的函数接口
在 C 中调用 Python 函数有多种方法,以下是其中的两种常见方法:使用 Python/C APIPython 提供了 C/C API,可以通过该 API 在 C 中调用 Python 函数。使用这种方法,需要先将 Python 解释器嵌入到 C 代码中,然后可以通过…...
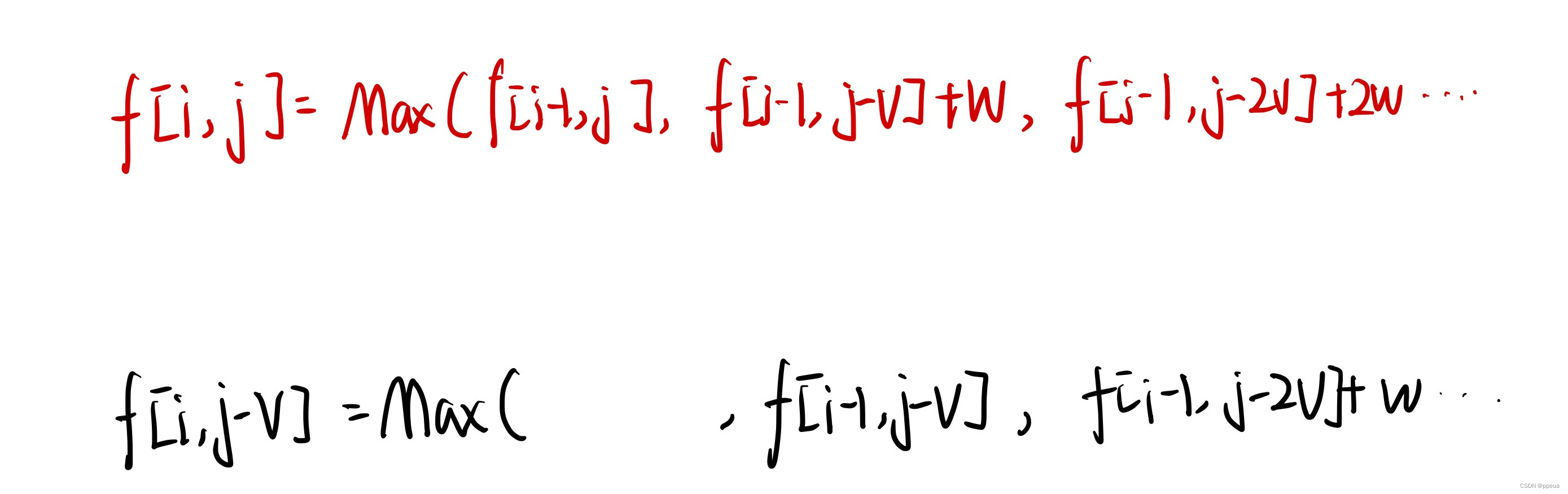
【动态规划】背包问题(01背包,完全背包)
Halo,这里是Ppeua。平时主要更新C语言,C,数据结构算法......感兴趣就关注我吧!你定不会失望。 🌈个人主页:主页链接 🌈算法专栏:专栏链接 我会一直往里填充内容哒! &…...
记录 UE5 完全重新构建 UE C++项目
不知道搞了什么,C项目的实时代码编译罢工了,搞了半天都修不好,只能又重建了 UE5 版本为 v5.1.1 删除以下文件夹 /Binaries /Intermediate /SavedBinaries 文件夹是编译后的模块 Intermediate 文件夹里是中间层的C代码,完全由ue…...
java版云HIS系统源码 微服务架构支持VUE
云his系统源码 一个好的HIS系统,要具有开放性,便于扩展升级,增加新的功能模块,支撑好医院的业务的拓展,而且可以反过来给医院赋能,最终向更多的患者提供更好地服务。 私信了解更多! 本套基于…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

工业安全零事故的智能守护者:一体化AI智能安防平台
前言: 通过AI视觉技术,为船厂提供全面的安全监控解决方案,涵盖交通违规检测、起重机轨道安全、非法入侵检测、盗窃防范、安全规范执行监控等多个方面,能够实现对应负责人反馈机制,并最终实现数据的统计报表。提升船厂…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

(二)TensorRT-LLM | 模型导出(v0.20.0rc3)
0. 概述 上一节 对安装和使用有个基本介绍。根据这个 issue 的描述,后续 TensorRT-LLM 团队可能更专注于更新和维护 pytorch backend。但 tensorrt backend 作为先前一直开发的工作,其中包含了大量可以学习的地方。本文主要看看它导出模型的部分&#x…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

IP如何挑?2025年海外专线IP如何购买?
你花了时间和预算买了IP,结果IP质量不佳,项目效率低下不说,还可能带来莫名的网络问题,是不是太闹心了?尤其是在面对海外专线IP时,到底怎么才能买到适合自己的呢?所以,挑IP绝对是个技…...
