AngularJS Web前端框架:深入探索与应用实践
AngularJS Web前端框架:深入探索与应用实践
AngularJS,作为一款强大的Web前端框架,为开发者提供了丰富的功能和工具,使得构建复杂且交互性强的Web应用变得更为便捷。本文将从四个方面、五个方面、六个方面和七个方面对AngularJS进行深入剖析,带您领略其魅力所在。
四个方面:AngularJS的核心特性
AngularJS以其独特的核心特性,赢得了广大开发者的青睐。首先,它采用了数据绑定机制,使得前端视图与后端数据能够实时同步,极大地提高了用户体验。其次,AngularJS支持模块化开发,使得代码更加清晰、可维护。此外,它还提供了丰富的指令和过滤器,方便开发者实现各种复杂的功能和效果。最后,AngularJS具有优秀的路由管理功能,使得单页面应用更加易于构建和管理。
五个方面:AngularJS的组件化开发
AngularJS的组件化开发理念使得前端开发更加高效和灵活。组件是AngularJS中的基本构建块,每个组件都具有独立的视图和逻辑,可以单独开发和szyg98.com测试。通过组合不同的组件,可以快速构建出功能丰富的Web应用。同时,组件之间的通信和数据共享也变得更加便捷和可靠。
六个方面:AngularJS的双向数据绑定
AngularJS的双向数据绑定是其最为核心的特性之一。它通过在视图和模型之间建立一个双向通道,使得两者之间的数据能够实时同步。当模型数据发生变化时,视图会自动更新;反之,当用户在视图中进行修改时,模型数据也会相应更新。这种机制极大地简化了前端开发的复杂度,提高了开发效率。
七个方面:AngularJS的依赖注入与测试
AngularJS的依赖注入机制使得代码更加灵活和可测试。通过依赖注入,开发者可以轻松地管理和替换组件之间的依赖关系,降低了代码之间的耦合度。同时,AngularJS还提供了强大的测试工具和方法,使得开发者能够对组件和整个应用进行全面的测试,确保应用的稳定性和可靠性。
然而,AngularJS作为一款强大的前端框架,也面临着一些挑战和www.szyg98.com争议。例如,随着前端技术的不断发展,出现了许多新的框架和库,使得AngularJS在某些方面显得稍显落后。此外,由于其自身的复杂性和学习曲线较陡,也使得一些初学者望而却步。
尽管如此,AngularJS仍然是一款值得学习和使用的Web前端框架。通过深入了解其核心特性和应用实践,我们可以充分发挥其优势,构建出高效、稳定且交互性强的Web应用。同时,我们也需要保持对新技术和新方法的关注和学习,以便在前端开发的道路上不断进步和创新。
相关文章:

AngularJS Web前端框架:深入探索与应用实践
AngularJS Web前端框架:深入探索与应用实践 AngularJS,作为一款强大的Web前端框架,为开发者提供了丰富的功能和工具,使得构建复杂且交互性强的Web应用变得更为便捷。本文将从四个方面、五个方面、六个方面和七个方面对AngularJS进…...

SQL 入门:使用 MySQL 进行数据库操作
SQL 入门:使用 MySQL 进行数据库操作 目录 引言SQL 基础 SQL 语言概述MySQL 简介 数据库设计基础 数据库与表的设计常见数据类型 MySQL 安装与配置 安装 MySQL基本配置与连接 基本 SQL 语句 数据库的创建与删除表的创建、修改与删除数据插入、更新与删除 数据查询…...
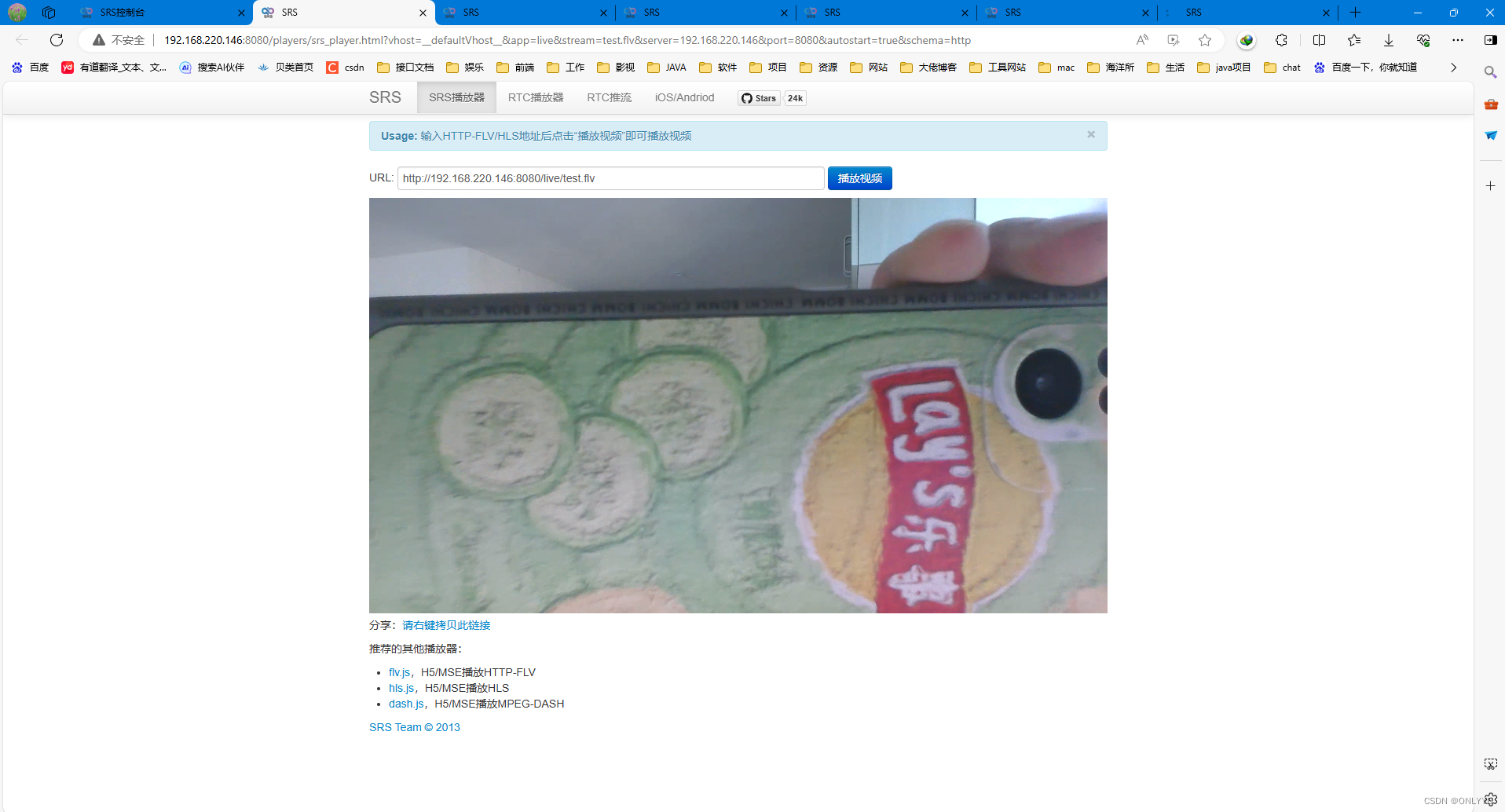
window安装ffmpeg播放本地摄像头视频
1、安装ffmpeg ffmpeg官方网站:FFmpeg 下载后解压文件夹名为ffmpeg 2、设置环境变量 目录 1、安装ffmpeg 设置环境变量 以F:\software\after\ffmpeg\bin为例 在命令行中输入ffmpeg出现下方代表安装成功 3、通过ffmpeg播放本地电脑摄像头 鼠标右击开始按钮&…...

【嵌入式DIY实例】-OLED显示网络时钟
OLED显示网络时钟 文章目录 OLED显示网络时钟1、硬件准备与接线2、代码实现在上一个ESP8266 NodeMCU文章中,我们用DS3231 RTC芯片和SSD1306 OLED制作了一个简单的实时时钟,时间和日期显示在SSD1306屏幕上,并且可以通过两个按钮进行设置。 在本中,我们将使用ESP 8266 NodeMC…...

【线程相关知识】
今日内容概要 开启线程的两种方式TCP服务端实现并发效果线程对象的join方法线程间数据共享线程对象属性及其他方法守护线程线程互斥锁GIL全局解释器锁多进程与多线程的实际应用场景 今日内容详细 开启线程的两种方式 # import time # from multiprocessing import Process #…...

鸿蒙ArkTS声明式开发:跨平台支持列表【透明度设置】 通用属性
透明度设置 设置组件的透明度。 说明: 开发前请熟悉鸿蒙开发指导文档: gitee.com/li-shizhen-skin/harmony-os/blob/master/README.md点击或者复制转到。 从API Version 7开始支持。后续版本如有新增内容,则采用上角标单独标记该内容的起始版…...

【SQL学习进阶】从入门到高级应用(九)
文章目录 子查询什么是子查询where后面使用子查询from后面使用子查询select后面使用子查询exists、not existsin和exists区别 union&union alllimit 🌈你好呀!我是 山顶风景独好 💕欢迎来到我的博客,很高兴能够在这里和您见面…...

Web前端三大主流框架技术分享
在当今快速发展的互联网时代,Web前端技术作为连接用户与服务的桥梁,其重要性不言而喻。随着技术的不断进步,为了提升开发效率、优化用户体验,一系列强大的前端框架应运而生。其中,Angular、React和Vue.js作为当前最为主…...

dockers安装mysql
1.dockerhub上搜索自己需要安装得镜像版本 dockerhub网址:https://hub-stage.docker.com docker pull mysql:5.7 #下载自己需要得版本2.启动容器实例,并且挂载容器数据卷 docker run -d -p 3306:3306 --privilegedtrue \ -v /home/mysql/log:/var/log/…...

100道面试必会算法-27-美团2024面试第一题-前缀和矩阵
100道面试必会算法-27-美团2024面试第一题-前缀和矩阵 问题解读 给定一个 n x n 的二进制矩阵,每个元素是 0 或 1。我们的任务是计算矩阵中所有边长为 k 的子矩阵中,包含特定数量 1 的情况。例如,我们希望找到所有边长为 k 的子矩阵中包含 k…...

从摇一摇到弹窗,AD无处不在?为了不再受打扰,推荐几款好用的屏蔽软件,让手机电脑更清爽
当我们沉浸在智能手机带来的便捷与乐趣中时,内置AD如同不速之客,时常打断我们的体验。 尤其是手机上那些“摇一摇”跳转,稍有不慎就会跳转到其他应用,令人不胜其烦。同样,电脑上的内置AD也如影随形,影响了我…...
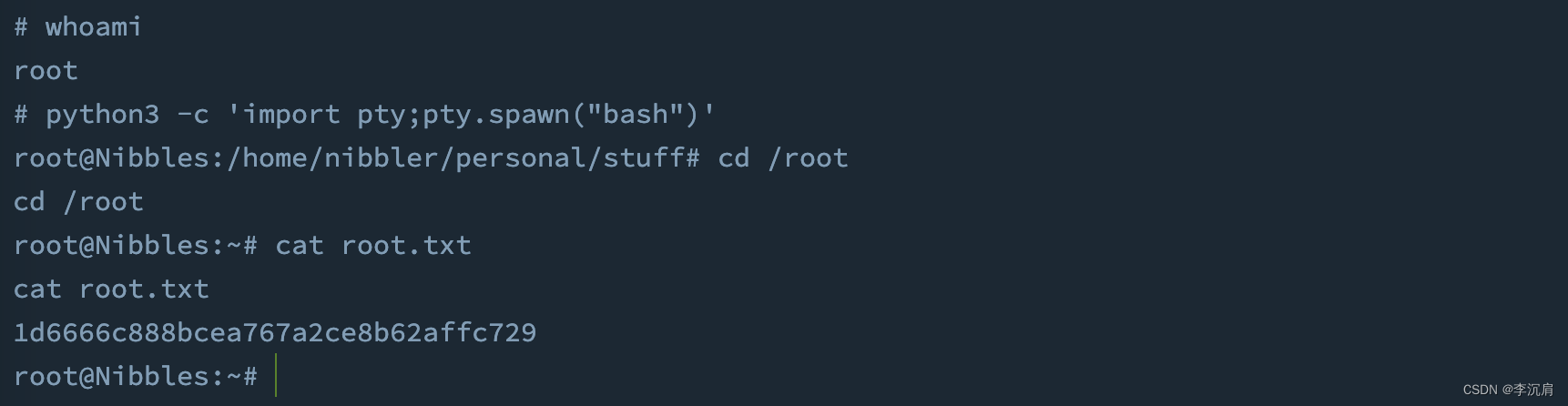
HackTheBox-Machines--Nibbles
Nibbles 测试过程 1 信息收集 NMAP 80 端口 网站出了打印出“Hello world!”外,无其他可利用信息,但是查看网页源代码时,发现存在一个 /nibbleblog 文件夹 检查了 http://10.129.140.63/nibbleblog/ ,发现了 /index.p…...

东方博宜1703 - 小明买水果
问题描述 小明去超市买了若干斤水果,你能根据水果的单价,小明买的水果数量,编一个程序计算出总金额,并打印出清单。 输入 输入两个值, 第一个为商品的单价,是一个小数。 第二个为商品的数量,…...
mac电脑用谷歌浏览器对安卓手机H5页面进行inspect
1、mac上在谷歌浏览器上输入 chrome://inspect 并打开该页面。 2、连接安卓手机到Mac电脑:使用USB数据线将安卓手机连接到Mac电脑。 3、手机上打开要的h5页面 Webview下面选择要的页面,点击inspect,就能像谷歌浏览器页面打开下面的页面&#…...
代码实践-深度学习基础-01基础函数的使用)
动手学深度学习(Pytorch版)代码实践-深度学习基础-01基础函数的使用
01基础函数的使用 主要内容 张量操作:创建和操作张量,包括重塑、填充、逐元素操作等。数据处理:使用pandas加载和处理数据,包括处理缺失值和进行one-hot编码。线性代数:包括矩阵运算、求和、均值、点积和各种范数计算…...

vm-bhyve:bhyve虚拟机的管理系统@FreeBSD
先说情况,当前创建虚拟机后网络没有调通....不明白是最近自己点背,还是确实有难度... 缘起: 前段时间学习bhyve虚拟机,发现bvm这个虚拟机管理系统,但是实践下来发现网络方面好像有问题,至少我花了两天时间…...
【Java】刚刚!突然!紧急通知!垃圾回收!
【Java】刚刚!突然!紧急通知!垃圾回收! 文章目录 【Java】刚刚!突然!紧急通知!垃圾回收!从C语言的内存管理引入:手动回收Java的垃圾回收机制引用计数器循环引用问题 可达…...
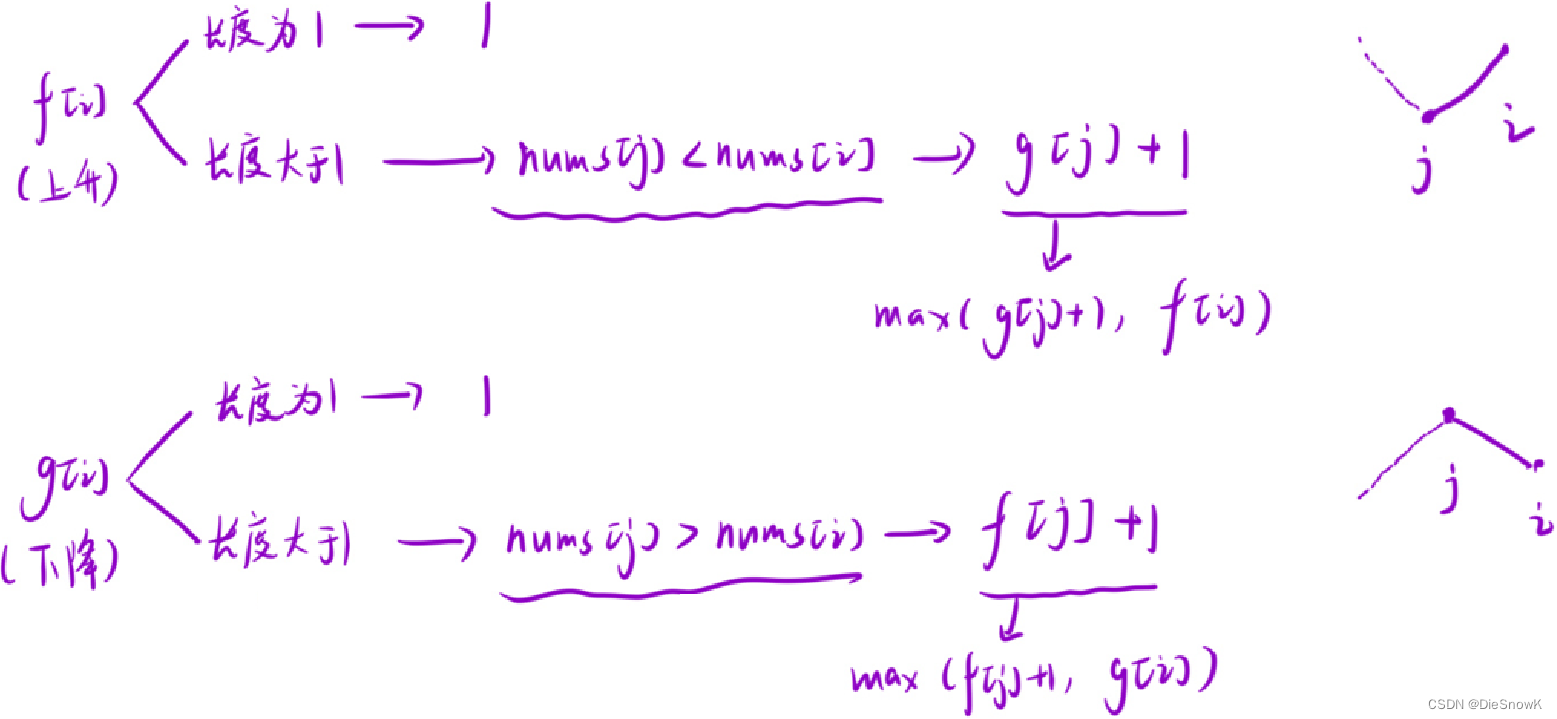
[Algorithm][动态规划][子序列问题][最长递增子序列][摆动序列]详细讲解
目录 0.子序列 vs 子数组1.最长递增子序列1.题目链接2.算法原理详解3.代码实现 2.摆动序列1.题目链接2.题目链接3.代码实现 0.子序列 vs 子数组 子序列: 相对顺序是跟源字符串/数组是一致的但是元素和元素之间,在源字符串/数组中可以是不连续的一般时间…...

【稳定检索】2024年心理学与现代化教育、媒体国际会议(PMEM 2024)
2024年心理学与现代化教育、媒体国际会议 2024 International Conference on Psychology and Modern Education and Media 【1】会议简介 2024年心理学与现代化教育、媒体国际会议即将召开,这是一场汇聚全球心理学、教育及媒体领域精英的学术盛宴。 本次会议将深入探…...
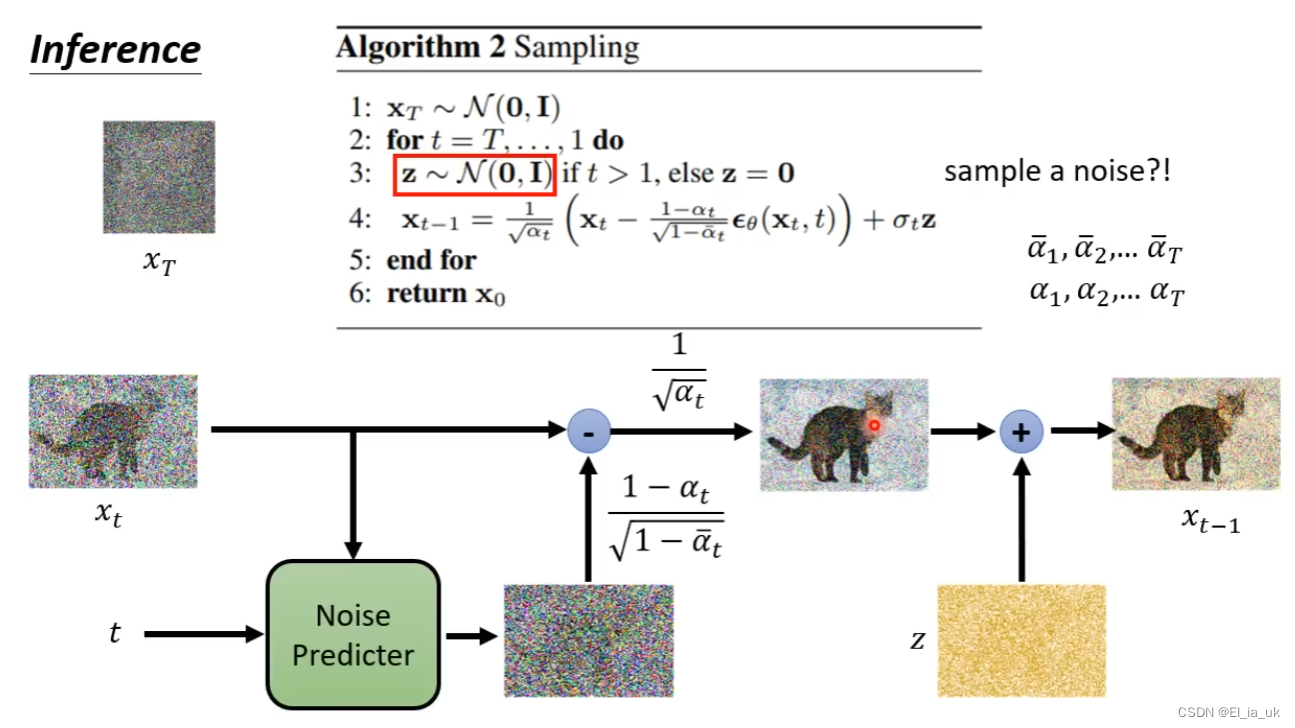
深入了解diffusion model
diffusion model是如何运作的 会输入当时noise的严重程度,根据我们的输入来确定在第几个step,并做出不同的回应。 Denoise模组内部实际做的事情 产生一张图片和产生noise难度是不一样的,若denoise 模块产生一只带噪声的猫说明这个模块已经会…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具,自己手写的难度,恐怕高级程序员花费一年的事件,也…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

Redis数据倾斜问题解决
Redis 数据倾斜问题解析与解决方案 什么是 Redis 数据倾斜 Redis 数据倾斜指的是在 Redis 集群中,部分节点存储的数据量或访问量远高于其他节点,导致这些节点负载过高,影响整体性能。 数据倾斜的主要表现 部分节点内存使用率远高于其他节…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...
