一、向量及其线性运算
🙌作者简介:数学与计算机科学学院出身、在职高校高等数学专任教师,分享学习经验、生活、 努力成为像代码一样有逻辑的人!
🌙个人主页:阿芒的主页
⭐ 高等数学专栏介绍:本专栏系统地梳理高等数学这门课的知识点,参考书主要为经典的同济版第七版《高等数学》以及作者在高校使用的《高等数学》系统教材。梳理《高等数学》这门课,旨在帮助那些刚刚接触这门课的小白以及需要系统复习这门课的考研人士。希望自己的一些经验能够帮助更多的人。
文章目录
- 向量的概念
- 向量的线性运算
- 空间直角坐标系
向量的概念
向量: 既有大小又有方向的量(又称矢量)
表示法: 有向线段 M1M2→\overrightarrow{M_1M_2}M1M2 或a→\overrightarrow{a}a
向径(矢径): 起点为原点的向量
自由向量: 与起点无关的向量
向量的模: 向量的大小,记作 ∣M1M2→∣|\overrightarrow{M_1M_2}|∣M1M2∣ 或∣a→∣|\overrightarrow{a}|∣a∣
单位向量: 模为1的向量
零向量: 模为0的向量,记作 0→\overrightarrow{0}0,或0
向量相等: 若向量a→\overrightarrow{a}a与b→\overrightarrow{b}b 大小相等,方向相同,记作a→=b→\overrightarrow{a}=\overrightarrow{b}a=b
负向量: 与 模相同,方向相反向量,记作 −a→-\overrightarrow{a}−a
向量共线: 由于平行向量可平移到同一直线上,故两向量平行又称两向量共线.
向量共面: 若 k(≥3)k(\geq 3)k(≥3)个向量经平移可移到同一平面上,则称此 kkk个向量共面.
向量的线性运算
-
向量的加法
运算法则: 满足平行四边形法则和三角形法则
注:三角形法则可推广到多个向量相加
运算规律:
①交换律 a→+b→=b→+a→\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{b}+\overrightarrow{a}a+b=b+a
②结合律(a→+b→)+c→=a→+(b→+c→)(\overrightarrow{a}+\overrightarrow{b})+\overrightarrow{c}=\overrightarrow{a}+(\overrightarrow{b}+\overrightarrow{c})(a+b)+c=a+(b+c) -
向量的减法
运算法则: 满足三角形法则
注:三角不等式关系(由三角形边长关系可证) -
向量的数乘
λ{\lambda}λ是一个数,λ{\lambda}λ与 a→\overrightarrow{a}a的乘积是一个新向量,记作 λa→\lambda\overrightarrow{a}λa
规定:λ>0{\lambda>0}λ>0时,λa→\lambda\overrightarrow{a}λa与a→\overrightarrow{a}a同向,∣λa→∣|\lambda\overrightarrow{a}|∣λa∣=λ∣a→∣\lambda|\overrightarrow{a}|λ∣a∣;
~~~~~~~~~ λ<0{\lambda<0}λ<0时,λa→\lambda\overrightarrow{a}λa与a→\overrightarrow{a}a反向,∣λa→∣|\lambda\overrightarrow{a}|∣λa∣=-λ∣a→∣\lambda|\overrightarrow{a}|λ∣a∣;
~~~~~~~~~ λ=0{\lambda=0}λ=0时,λa→\lambda\overrightarrow{a}λa=0→\overrightarrow{0}0.
总之:∣λa→∣|\lambda\overrightarrow{a}|∣λa∣=∣λ∣∣a→∣|\lambda||\overrightarrow{a}|∣λ∣∣a∣
运算规律:
①结合律:λ(μ)a→\lambda(\mu)\overrightarrow{a}λ(μ)a=μ(λa→)\mu(\lambda\overrightarrow{a})μ(λa)=λμa→\lambda\mu\overrightarrow{a}λμa
②分配律:(λ+μ)a→(\lambda+\mu)\overrightarrow{a}(λ+μ)a=λa→+μa→\lambda\overrightarrow{a}+\mu\overrightarrow{a}λa+μa
~~~~~~~~~~~~~~~ λ(a→+b→)\lambda(\overrightarrow{a}+\overrightarrow{b})λ(a+b)=λa→+λb→\lambda\overrightarrow{a}+\lambda\overrightarrow{b}λa+λb
注:若a→≠0→\overrightarrow{a}\neq\overrightarrow{0}a=0,则有单位向量a→°=a→∣a→∣\overrightarrow{a}^{°}=\frac{\overrightarrow{a}}{|\overrightarrow{a}|}a°=∣a∣a.因此a→\overrightarrow{a}a=∣a→∣|\overrightarrow{a}|∣a∣a→°\overrightarrow{a}^{°}a°
向量共线定理:设a→\overrightarrow{a}a为非零向量,则a→∥b→\overrightarrow{a}\parallel\overrightarrow{b}a∥b ⟺\Longleftrightarrow⟺b→\overrightarrow{b}b=λa→\lambda\overrightarrow{a}λa(λ\lambdaλ为唯一 实数).
空间直角坐标系
概念: 过空间一定点O,由三条互相垂直的数轴按右手规则组成一个空间直角坐标系.
构成: 坐标原点:O(0,0,0)
~~~~~~~~~~~ 坐标轴: x轴、y轴、z轴
~~~~~~~~~~~ 坐标面:xoy面、yoz面、xoz面
~~~~~~~~~~~ 卦限(八个)
卦限符号特征:
| 卦限 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ | Ⅵ | Ⅶ | Ⅷ |
|---|---|---|---|---|---|---|---|---|
| x | + | - | - | + | + | - | - | + |
| y | + | + | - | - | + | + | - | - |
| z | + | + | + | + | - | - | - | - |
相关文章:

一、向量及其线性运算
🙌作者简介:数学与计算机科学学院出身、在职高校高等数学专任教师,分享学习经验、生活、 努力成为像代码一样有逻辑的人! 🌙个人主页:阿芒的主页 ⭐ 高等数学专栏介绍:本专栏系统地梳理高等数学…...

Spring Cloud/Spring Cloud Alibaba核心知识总结
Spring Cloud核心知识总结 springCloud是一个服务治理平台,若干个框架的集合,提供了全套的分布式系统的解决方案。包含:服务注册与发现、配置中心、服务网关、智能路由、负载均衡、断路器、监控跟踪、分布式消息、分布式事务等等。 SpringC…...
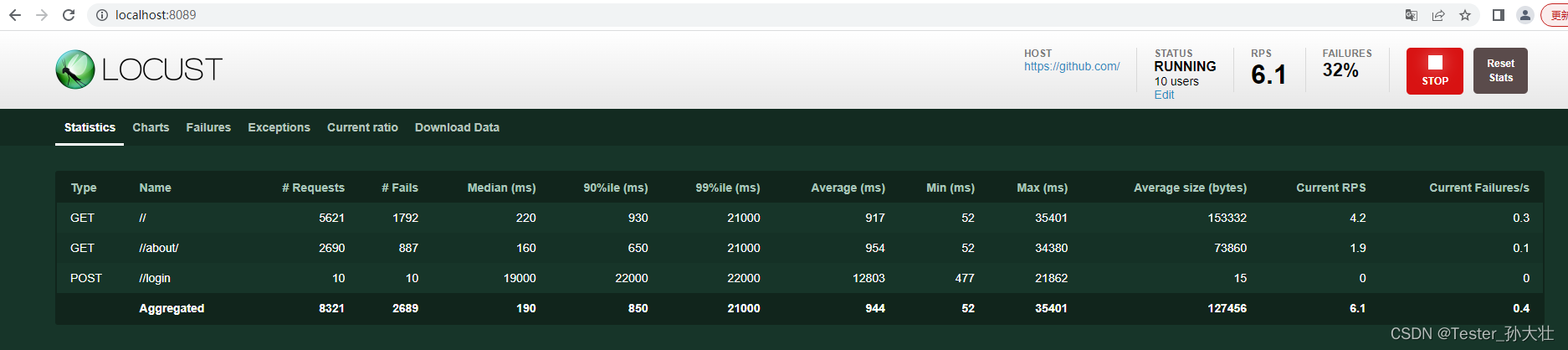
Locust框架从0到1入门
Locust介绍 Locust是使用Python语言编写实现的开源性能测试工具,可以用来测试Web应用程序、API、数据库等各种应用程序的性能,使用起来简洁、轻量、高效,并发机制基于gevent协程,可以实现单机模拟生成较高的并发压力。中文意为&a…...
表示范围)
C++:整数(short ,int,long,long long)表示范围
整形 C用short、int、long 、long long来表示整数的整形,同一整形也分为有符号(signed)和无符号(unsigned)两种。数据长度与操作系统和编译器的位数有关,其能够表示的范围也有所不同。接下来本文将用代码的…...
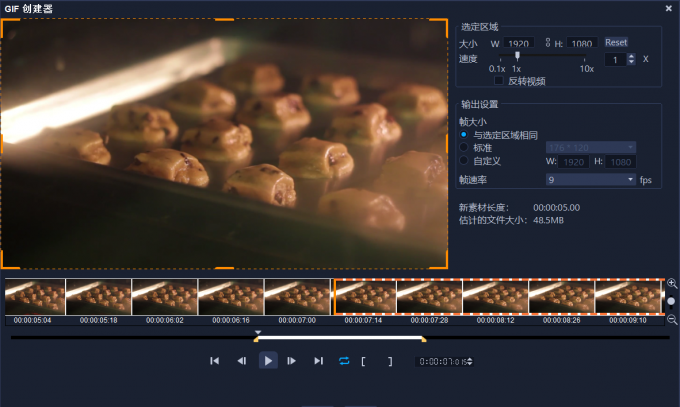
会声会影2023旗舰版新功能介绍,Corel VideoStudio Ultimate2023以及电脑系统配置要求
会声会影2023中文旗舰版功能非常强大的视频编辑软件,非常专业的使用效果,会声会影2023中文版可以针对剪辑电影进行使用,非常强大的色彩校正方式,无论什么光线下进行拍摄,都可以通过后期进行调整,并且里面超…...

软件测试用例篇(5)
测试是否运行代码去划分? 1)静态测试: 不运行代码,检查代码的风格,格式是否符合公司的标准规范,检查代码的逻辑结构是否满足需求要实现的功能 看代码,不运行代码,通过静态分析代码的语法,编写规…...

三个修饰符
三个修饰符三个修饰符一、abstract1.1 修饰类1.2 修饰方法二、final2.1 修饰类2.2 修饰方法2.3 修饰变量2.3.1 修饰属性2.3.2 修饰局部变量2.3.3 修饰方法的参数2.3.4 常量三、static关键字3.1 修饰属性3.2 修饰方法3.3 修饰代码块3.4 继承时的执行顺序三个修饰符 一、abstrac…...

JVM调优面试题——参数命令专题
文章目录1、JVM参数有哪些?1.1、 标准参数1.2、-X参数1.3、 -XX参数1.4、 其他参数1.5、 查看参数1.6、 设置参数的常见方式1.7、 常用参数含义2、JVM常用命令有哪些?2.1、jps2.2、jinfo2.3、jstat2.4、jstack2.5、jmap3、你会估算GC频率吗?4、 内存溢出…...
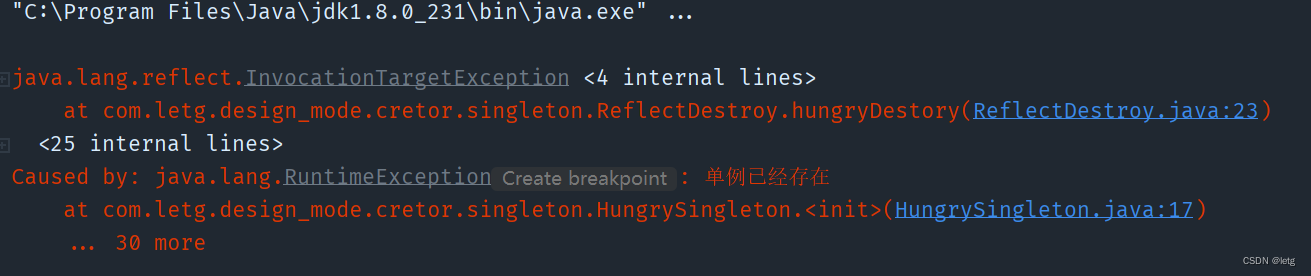
单例模式(设计模式详解)
单例模式 描述 单例模式是一种创建型模式,它的目的是确保一个类只有一个实例,并提供全局访问点。这个实例可以被多个客户端共享,从而避免创建多个实例所带来的资源浪费和不必要的复杂性。 实现 懒汉模式 public class LasySingleton {priv…...

设计一份关于文化遗产视频的调查问卷
参考文献:[1]任洁. 重庆美食类短视频传播策略研究[D].重庆交通大学,2021.DOI:10.27671/d.cnki.gcjtc.2021.000699.📰1 设计背景现已制作一些关于文化遗产的时长4-5分钟的视频,需要面向在校大学生收集他们对视频的看法从而分析视频的传播效果&…...
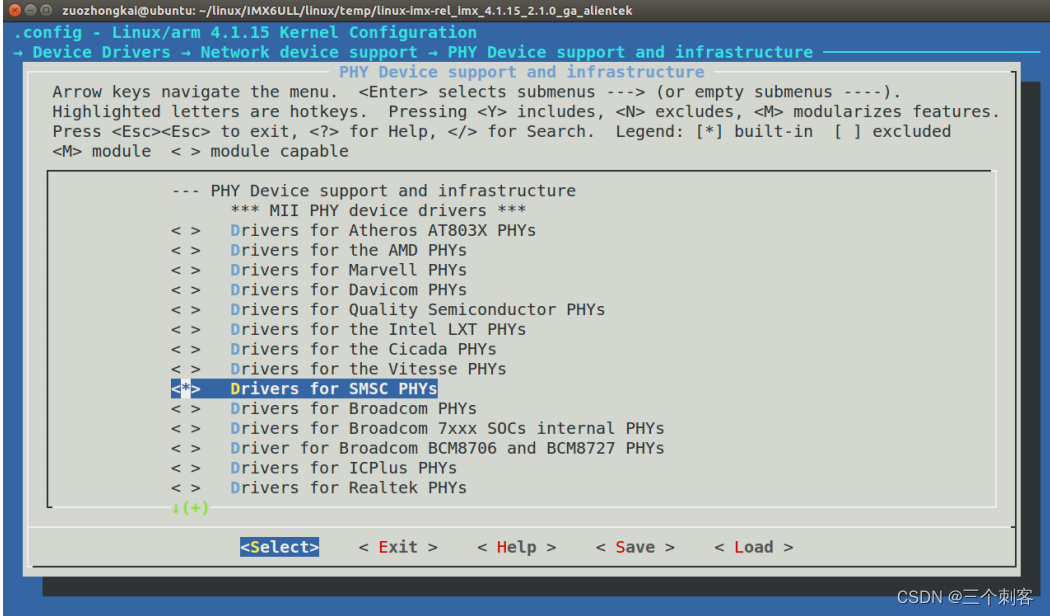
Linux内核移植
内核移植半导体厂商会从linux内核官网下载某个版本,将其移植到自己的CPU上,测试成功后就会将其开放给该半导体的厂商的CPU开发者,开发者下载其提供的linux内核,然后将其移植到自己的 产品上。1、NXP官方开发板Linux内核编译测试编…...

忆享科技优化入职培训加强人效管理全面迎接新挑战
-优化入职培训-忆享科技加强人效管理入职培训课程 ✦ KPI系统上线 ✦ 砥砺前行前言许多企业随着自身的不断发展,对于各类人才引进需求也越来越迫切,一批批新员工的加入,公司规模逐渐扩大,给公司带来了全新的血液。但在大量新员工加…...
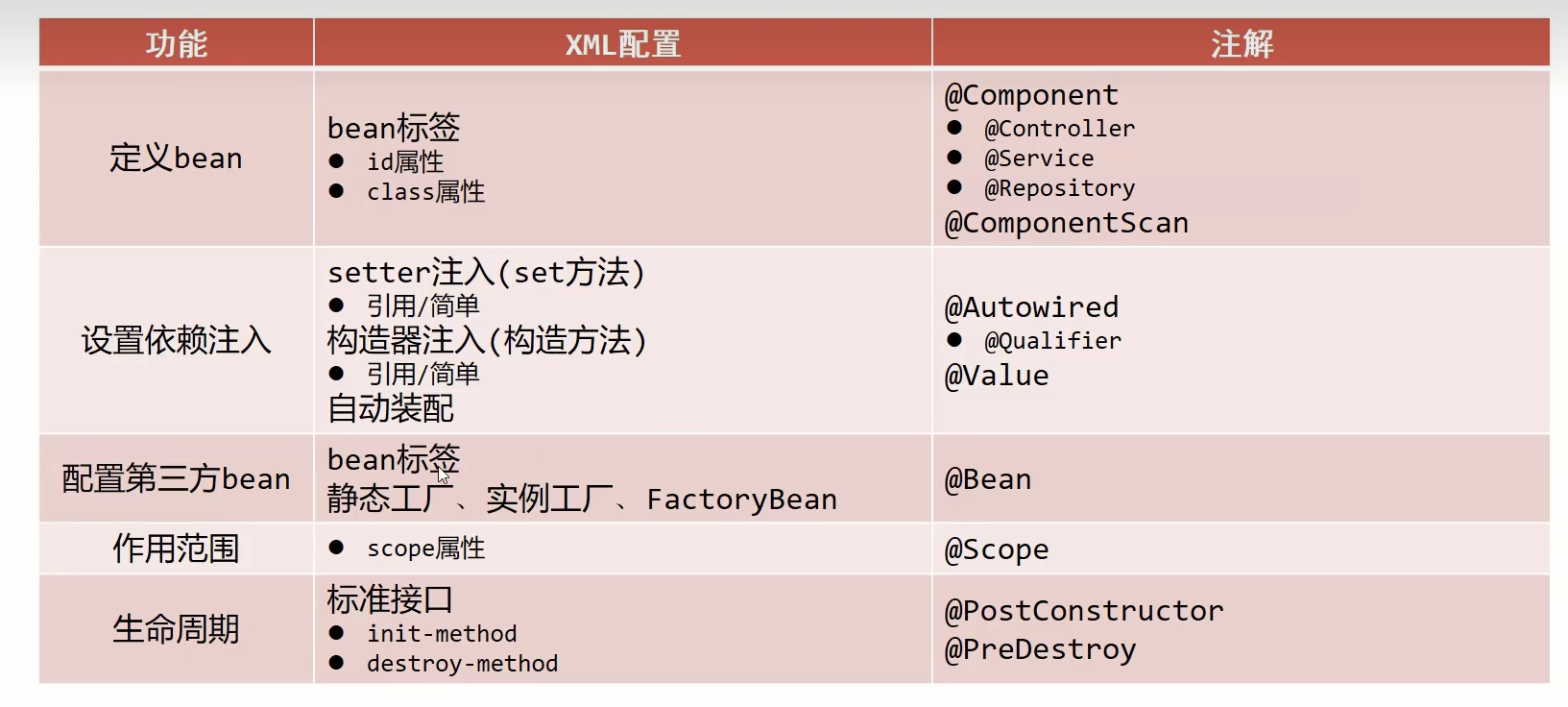
Spring——注解开发依赖注入和管理第三方bean
自动装配(引用类型) 环境准备: 文件结构如下图所示,Dao层的实现类里面有一个save方法,Service层里面的实现类有一个BookDao的声明和一个set方法,同时也有一个save方法,配置类的扫描范围如图所示 在当前的一个测试类当…...
)
shell可能考你但是不常用的基础($篇)
前言 当你面试的时候,可能要说的架构什么都准备好了,也说的七七八八,结果到最后问了一些基础的问题答不上来或者没想起来就很容易造成社会性死亡,一个没答上来道心被破,后面就更容易懵逼了 通常造成这个问题的原因是写…...

项目管理必备:如何绘制一份优秀的甘特图?
本文一共分为两部分—— 分享60Excel甘特图模板,简单省事儿分享两种甘特图制作教程,高效快捷 第一部分——60甘特图模板 分享一些项目管理甘特图的模板,省事儿!高效!简单! Excel甘特图表模板自取…...
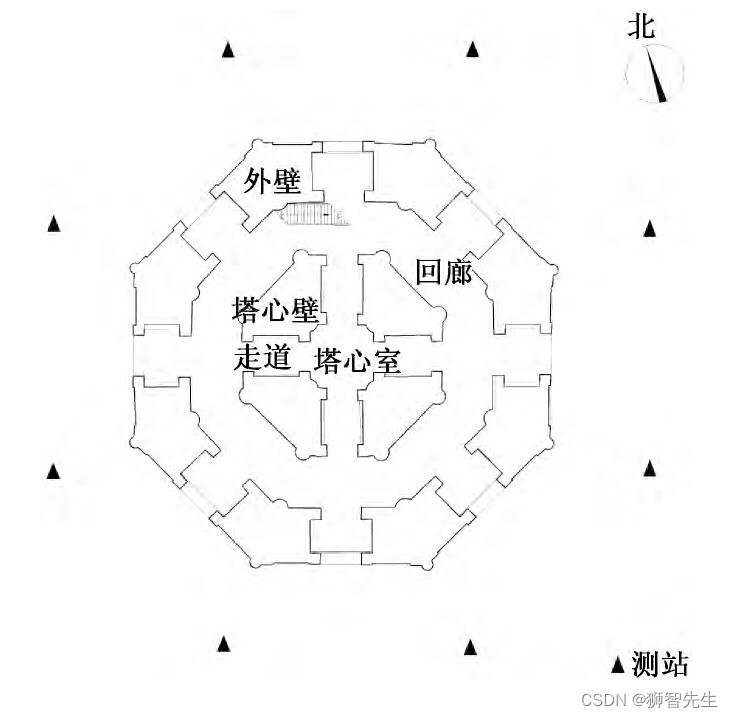
【点云学习】多时相激光雷达点云
多时相雷达数据(multi-tempral LiDAR data) 1 一种多时相激光雷达数据建筑物变化检测方法-汪承义(2013) 背景:空间分辨率的提高引入了“类内可分性”增加与“类间可分性”降低;遮挡与阴影的存在使问题变得…...

使用QT C++编写一个随机生成网络ip地址的程序
根据网络搜索结果,使用QT C编写一个随机生成网络ip地址的程序的示例代码可能如下: cpp #include <QCoreApplication> #include <QRandomGenerator> #include <QDebug> int main(int argc, char *argv[]) { QCoreApplication a(a…...

Web前端学习:章三 -- JavaScript预热(三)
六九:函数的变量提升 函数的变量提升没有var高,var是最高的。 先提var,再提函数 解析: 1、4行打印之前没有定义变量,预解析触发变量提升 2、先提var,再提函数。所以先把var提升到最上面,然后提…...

java实用小技巧:判断list是否有重复项
在项目中经常会遇到这样的场景,就是一个list,根据某种规则,我要去判断里面是不是有重复的项。 难度不高,但有点烦,所以专门开一篇文章来记录一下,争取弄一个相对简洁的写法。 先看一个简单的例子…...
)
SQL优化常用招数(上)
文章目录 一、查询SQL尽量不要使用select *,而是具体字段二、避免在where子句中使用 or 来连接条件三、尽量使用数值替代字符串类型四、使用varchar代替char五、技术延伸,char与varchar2的区别?六、where中使用默认值代替null七、避免在where子句中使用!=或<>操作符八…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

【JVM】- 内存结构
引言 JVM:Java Virtual Machine 定义:Java虚拟机,Java二进制字节码的运行环境好处: 一次编写,到处运行自动内存管理,垃圾回收的功能数组下标越界检查(会抛异常,不会覆盖到其他代码…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

pikachu靶场通关笔记22-1 SQL注入05-1-insert注入(报错法)
目录 一、SQL注入 二、insert注入 三、报错型注入 四、updatexml函数 五、源码审计 六、insert渗透实战 1、渗透准备 2、获取数据库名database 3、获取表名table 4、获取列名column 5、获取字段 本系列为通过《pikachu靶场通关笔记》的SQL注入关卡(共10关࿰…...

selenium学习实战【Python爬虫】
selenium学习实战【Python爬虫】 文章目录 selenium学习实战【Python爬虫】一、声明二、学习目标三、安装依赖3.1 安装selenium库3.2 安装浏览器驱动3.2.1 查看Edge版本3.2.2 驱动安装 四、代码讲解4.1 配置浏览器4.2 加载更多4.3 寻找内容4.4 完整代码 五、报告文件爬取5.1 提…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

JVM虚拟机:内存结构、垃圾回收、性能优化
1、JVM虚拟机的简介 Java 虚拟机(Java Virtual Machine 简称:JVM)是运行所有 Java 程序的抽象计算机,是 Java 语言的运行环境,实现了 Java 程序的跨平台特性。JVM 屏蔽了与具体操作系统平台相关的信息,使得 Java 程序只需生成在 JVM 上运行的目标代码(字节码),就可以…...

JavaScript 数据类型详解
JavaScript 数据类型详解 JavaScript 数据类型分为 原始类型(Primitive) 和 对象类型(Object) 两大类,共 8 种(ES11): 一、原始类型(7种) 1. undefined 定…...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...
