数据结构——哈夫曼树编程,输入权值实现流程图代码
一、须知
本代码是在数据结构——哈夫曼树编程上建立的,使用时需将代码剪切到C++等软件中。需要输入权值方可实现流程图,但是还需要按照编程换算出的结果自己用笔画出流程图。
下面将代码粘贴到文章中,同时举一个例子:
二、代码段
#include "stdio.h"
#define MAXLEN 100
typedef struct //定义本机构体
{int weight; //定义一个整形权值的变量int lchild,rchild,parent; //分别定义左孩子、右孩子及双亲指针
}HTNode;
typedef HTNode HT[MAXLEN]; //表明向量的类型
int n; //定义整形变量n
//-----------------初始化子函数---------------------------------------------
void InitHFMT (HT T)
{ int i;printf("\n请输入权值的总数(需小于100):");scanf("%d",&n);for(i=0;i<2*n-1;i++){T[i].weight=0;T[i].lchild=-1;T[i].rchild=-1;T[i].parent=-1;}
}
//-----------------输入权值子函数--------------------------------------------
void InputWeight (HT T)
{int w,i;for(i=0;i<n;i++){printf("请输入第%d个权值:",i+1);scanf("%d",&w);getchar();T[i].weight=w;}
}
//-----------------选择两个结点中小的结点------------------------------------
void SelectMin (HT T,int i,int *pl,int *p2)
{long minl=888888,min2=888888; //设两个长整型数值,并使它大于可能会出现的最大权值int j;for(j=0;j<=i;j++){if(T[j].parent==-1){if(minl>T[j].weight){ minl=T[j].weight; //找出最小权值*pl=j; //通过*p1带回序号}}
}for (j=0;j<=i;j++){ if(T[j].parent==-1){ if (min2>T[j].weight&&j!=(*pl)){ min2=T[j].weight; //找出第二最小权值*p2=j; //通过*p2带回序号}}}
}
//-----------------构造哈夫曼树,T[2*n-1]为根节点-----------------------------void CreatHFMT (HT T){int i,pl,p2;InitHFMT (T);InputWeight(T);for(i=n;i<2*n-1;i++){ SelectMin(T,i-1,&pl,&p2);T[pl].parent=T[p2].parent=i;T[i].lchild=T[pl].weight;T[i].rchild=T[p2].weight;T[i].weight=T[pl].weight+T[p2].weight;}}
//-----------------输出向量状态表----------------------------------------------
void printHFMT (HT T)
{ int i;printf("\n哈夫曼树的两边显示为(建议由下往上看/画):\n");for(i=0;i<2*n-1;i++)while(T[i].lchild!=-1){printf("(两边和为%d,左边值为%d,右边值为%d)\n",T[i].weight,T[i].lchild,T[i].rchild);break;}
}
//-----------------哈夫曼编码函数----------------------------------------------
void hfnode(HT T,int i,int j)
{j=T[i].parent;if (T[j].rchild==T[i].weight)printf("1");elseprintf("0");if(T[j].parent!=-1)i=j,hfnode (T,i,j);
}
//-----------------求哈夫曼树编码----------------------------------------------
void huffmannode(HT T)
{int i,j,a;printf("\n输入的权值的对应哈夫曼树编码(下面的哈夫曼编码树是由下往上排序的!!!):");for (i=0;i<n;i++){j=0;a=i;printf("\n%i的编码为:",T[i].weight);hfnode(T,i,j);i=a;}
}
//-----------------主函数-------------------------------------------------------
void main()
{ HT HT;CreatHFMT(HT);printHFMT(HT);huffmannode(HT);printf("\n ");
}
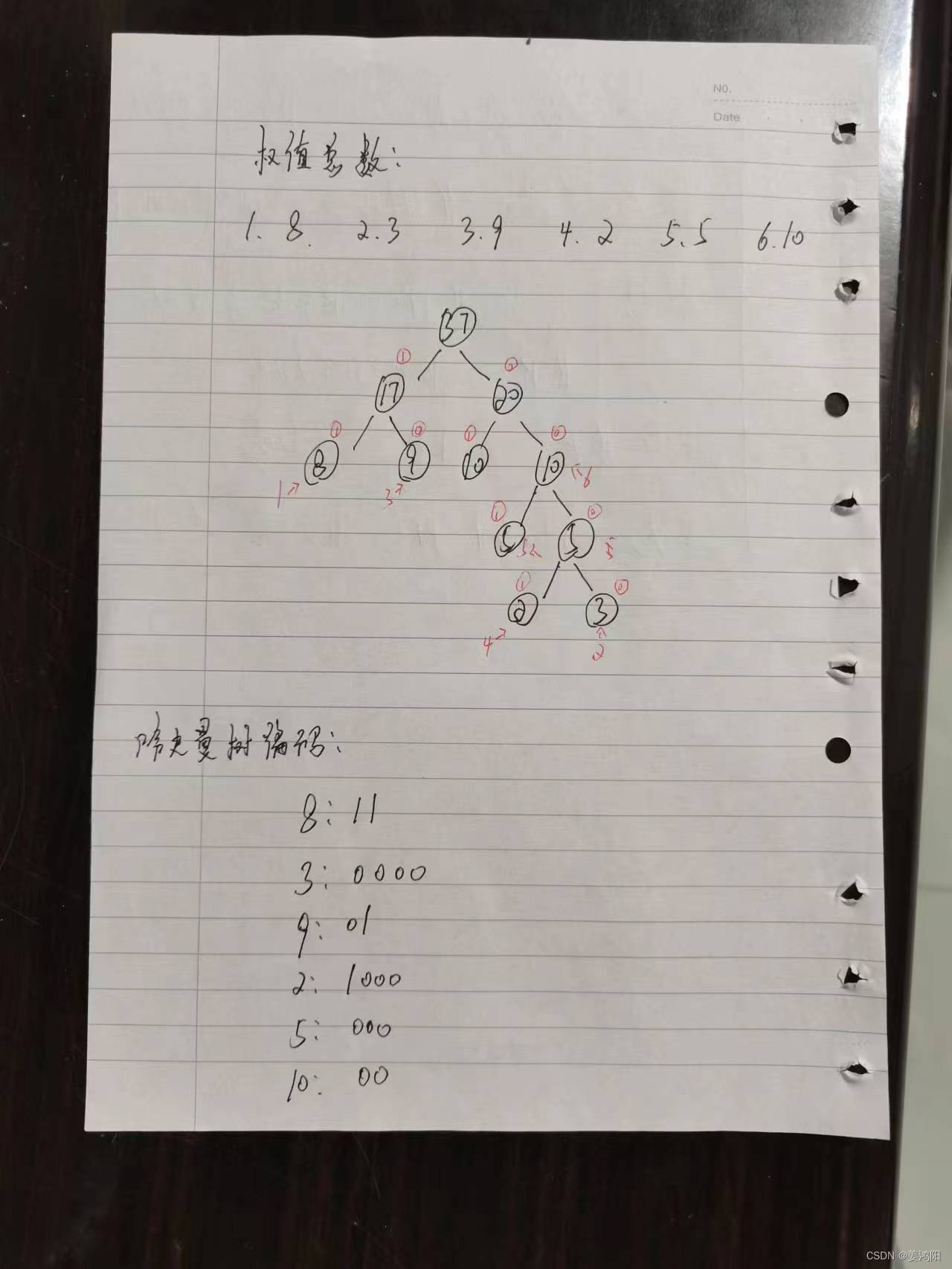
三、举例(流程图)
1.首先输入:权值总数以及各个权值,编程便可实现;

2.按照代码画流程图,以上面图片的权值举例,在编程结果出来后:首先看两面的数值,
先看最后一行的和为37,那么流程图的总数(最高点)便变为37
其次37的下面左边值为17,右边值为20
在看上一行,和为20,那么对照代码下一行两边的值可知,右边值为20
所以在右边值下的左边值和右边值分别为10
依次往上,就不都举例了······
本编程的哈夫曼树编码有问题,其所给的数值与实际答案是相反的列入9的变为为10,那么他真正的编码为01。就是1为0,0为1.
四、结语
本编程是能快速实现哈夫曼树的编码结果,有基础的同学看一下流程就知道是什么回事了,基础差的需要慢慢理解,本文章就不详细再讲了,同时这个代码有些错误,用能力者可以修改调试,实现更加完美的程序!
相关文章:

数据结构——哈夫曼树编程,输入权值实现流程图代码
一、须知 本代码是在数据结构——哈夫曼树编程上建立的,使用时需将代码剪切到C等软件中。需要输入权值方可实现流程图,但是还需要按照编程换算出的结果自己用笔画出流程图。 下面将代码粘贴到文章中,同时举一个例子:二、代…...
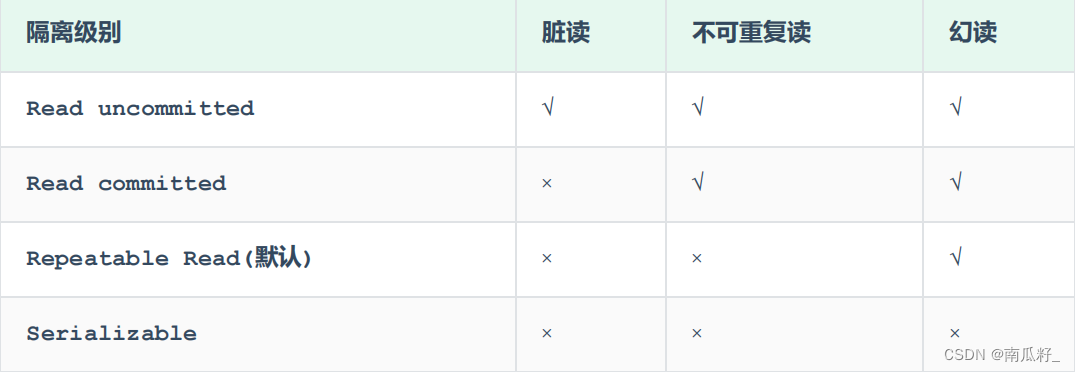
【MySQL】 事务
😊😊作者简介😊😊 : 大家好,我是南瓜籽,一个在校大二学生,我将会持续分享Java相关知识。 🎉🎉个人主页🎉🎉 : 南瓜籽的主页…...

Java测试——selenium常见操作(2)
这篇博客继续讲解一些selenium的常见操作 selenium的下载与准备工作请看之前的博客:Java测试——selenium的安装与使用教程 先创建驱动 ChromeDriver driver new ChromeDriver();等待操作 我们上一篇博客讲到,有些时候代码执行过快,页面…...
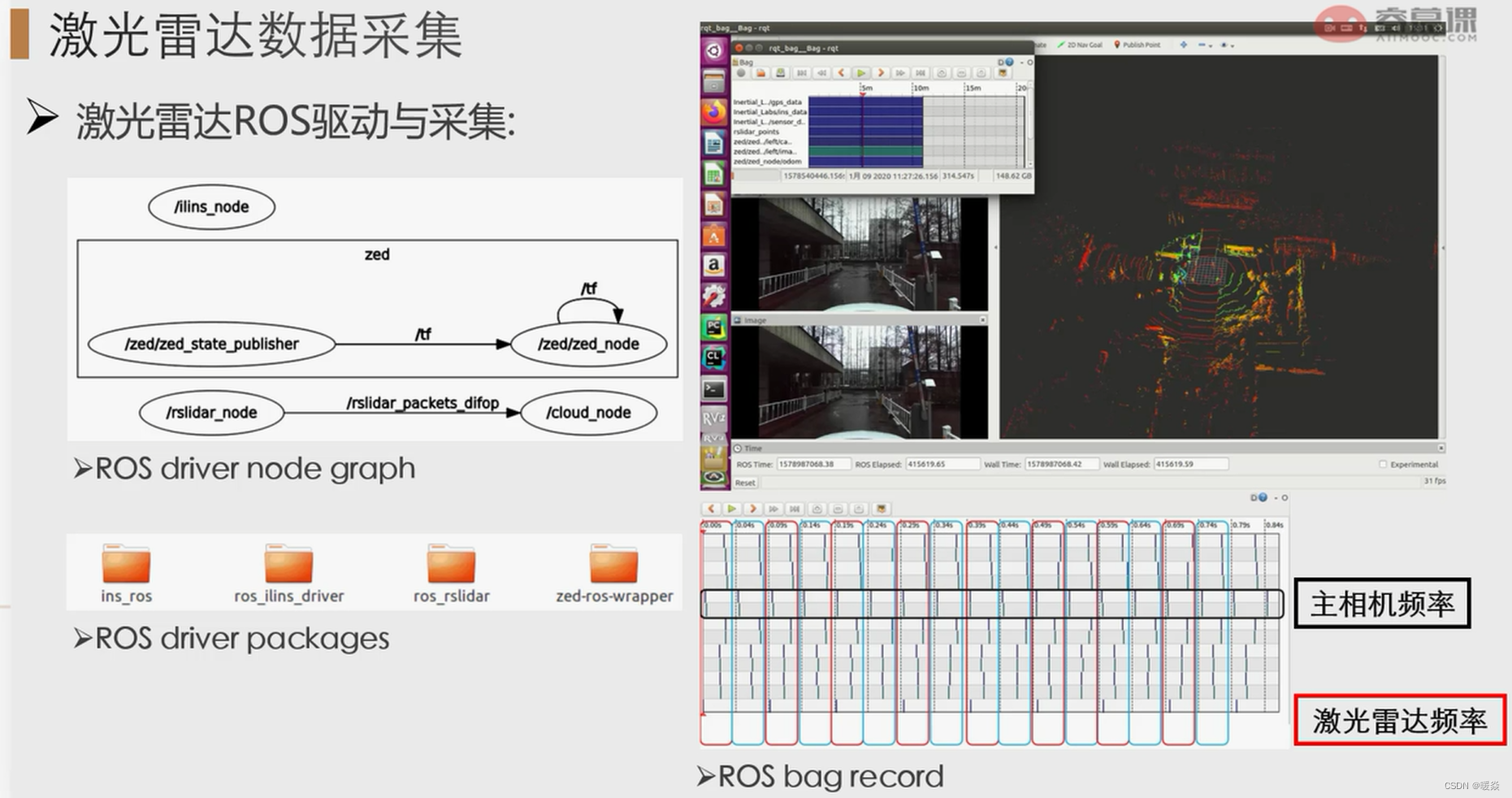
【三维点云】01-激光雷达原理与应用
文章目录内容概要1 激光雷达原理1.1 什么是激光雷达?1.2 激光雷达原理1.3 激光雷达分类三角法TOF法脉冲间隔测量法幅度调制的相位测量法相干法激光雷达用途2 激光雷达安装、标定与同步2.1 激光雷达安装方式考虑因素2.2 激光雷达点云用途2.3 数据融合多激光雷达数据融…...

自动驾驶感知——物体检测与跟踪算法|4D毫米波雷达
文章目录1. 物体检测与跟踪算法1.1 DBSCAN1.2 卡尔曼滤波2. 毫米波雷达公开数据库的未来发展方向3. 4D毫米波雷达特点及发展趋势3.1 4D毫米波雷达特点3.1.1 FMCW雷达角度分辨率3.1.2 MIMO ( Multiple Input Multiple Output)技术3.2 4D毫米波雷达发展趋势3.2.1 芯片级联3.2.2 专…...

C语言(内联函数(C99)和_Noreturn)
1.内联函数 通常,函数调用都有一定的开销,因为函数的调用过程包含建立调用,传递参数,跳转到函数代码并返回。而使用宏是代码内联,可以避开这样的开销。 内联函数:使用内联diamagnetic代替函数调用。把函数…...
理解与tensorflow2.0 代码实现 附完整代码)
图卷积神经网络(GCN)理解与tensorflow2.0 代码实现 附完整代码
图(Graph),一般用 $G=(V,E)$ 表示,这里的$V$是图中节点的集合,$E$ 为边的集合,节点的个数用$N$表示。在一个图中,有三个比较重要的矩阵: 特征矩阵$X$:维度为 $N\times D$ ,表示图中有 N 个节点,每个节点的特征个数是 D。邻居矩阵$A$:维度为 $N\times N$ ,表示图中 N…...
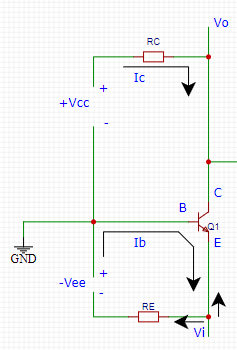
模电学习6. 常用的三极管放大电路
模电学习6. 常用的三极管放大电路一、判断三极管的工作状态1. 正偏与反偏的概念2. 工作状态的简单判断二、三种重要的放大电路1. 共射电路2. 共集电极放大电路3. 共基极放大电路一、判断三极管的工作状态 1. 正偏与反偏的概念 晶体管分P区和N区, 当P区电压大于N区…...
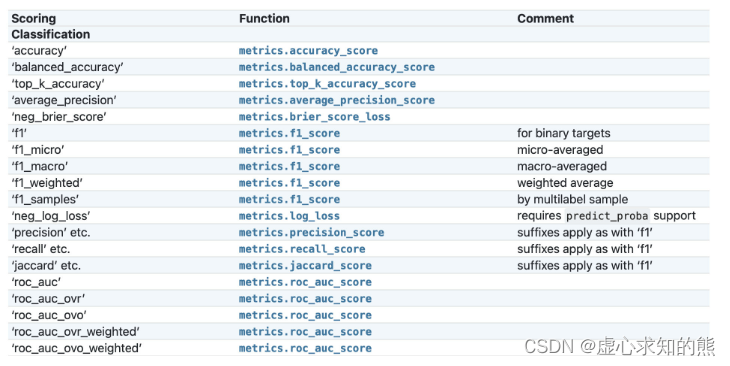
Lesson 6.6 多分类评估指标的 macro 和 weighted 过程 Lesson 6.7 GridSearchCV 的进阶使用方法
文章目录一、多分类评估指标的 macro 和 weighted 过程1. 多分类 F1-Score 评估指标2. 多分类 ROC-AUC 评估指标二、借助机器学习流构建全域参数搜索空间三、优化评估指标选取1. 高级评估指标的选用方法2. 同时输入多组评估指标四、优化后建模流程在正式讨论关于网格搜索的进阶…...
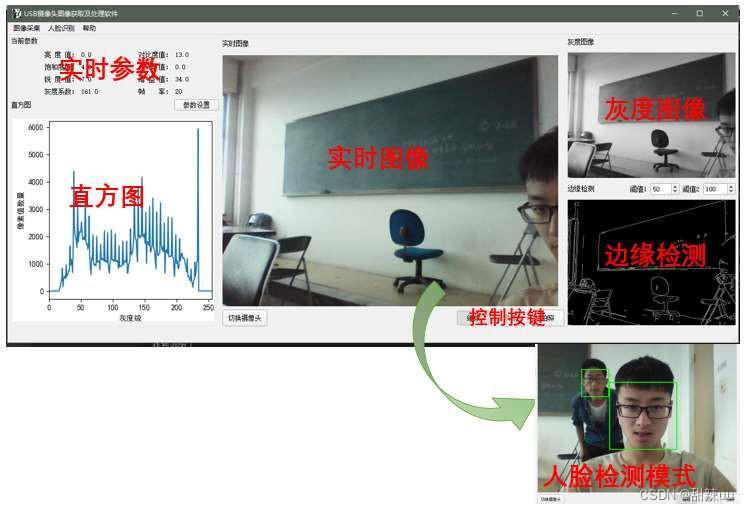
基于 Python 实时图像获取及处理软件图像获取;图像处理;人脸识别设计 计算机毕设 附完整代码+论文 +报告
界面结果:图像获取;图像处理;人脸识别 程序结构设计 图形用户界面设计与程序结构设计是互为表里的。或者说,程序结构设计是软件设计最本质、最核心的内容。徒有界面而内部逻辑结构混乱的软件一无是处。 Windows 操作系统是一款图形化的操作系统,相比于早期的计算机使用的命…...
前后端RSA互相加解密、加签验签、密钥对生成(Java)
目录一、序言二、关于PKCS#1和PKCS#8格式密钥1、简介2、区别二、关于JSEncrypt三、关于jsrsasign四、前端RSA加解密、加验签示例1、相关依赖2、cryptoUtils工具类封装3、测试用例五、Java后端RSA加解密、加验签1、CryptoUtils工具类封装2、测试用例六、前后端加解密、加验签交互…...

基于Java+SpringBoot+Vue前后端分离学生宿舍管理系统设计与实现
博主介绍:✌全网粉丝3W,全栈开发工程师,从事多年软件开发,在大厂呆过。持有软件中级、六级等证书。可提供微服务项目搭建、毕业项目实战、项目定制✌ 博主作品:《微服务实战》专栏是本人的实战经验总结,《S…...
)
前端高频面试题—JavaScript篇(二)
💻前端高频面试题—JavaScript篇(二) 🏠专栏:前端面试题 👀个人主页:繁星学编程🍁 🧑个人简介:一个不断提高自我的平凡人🚀 🔊分享方向…...
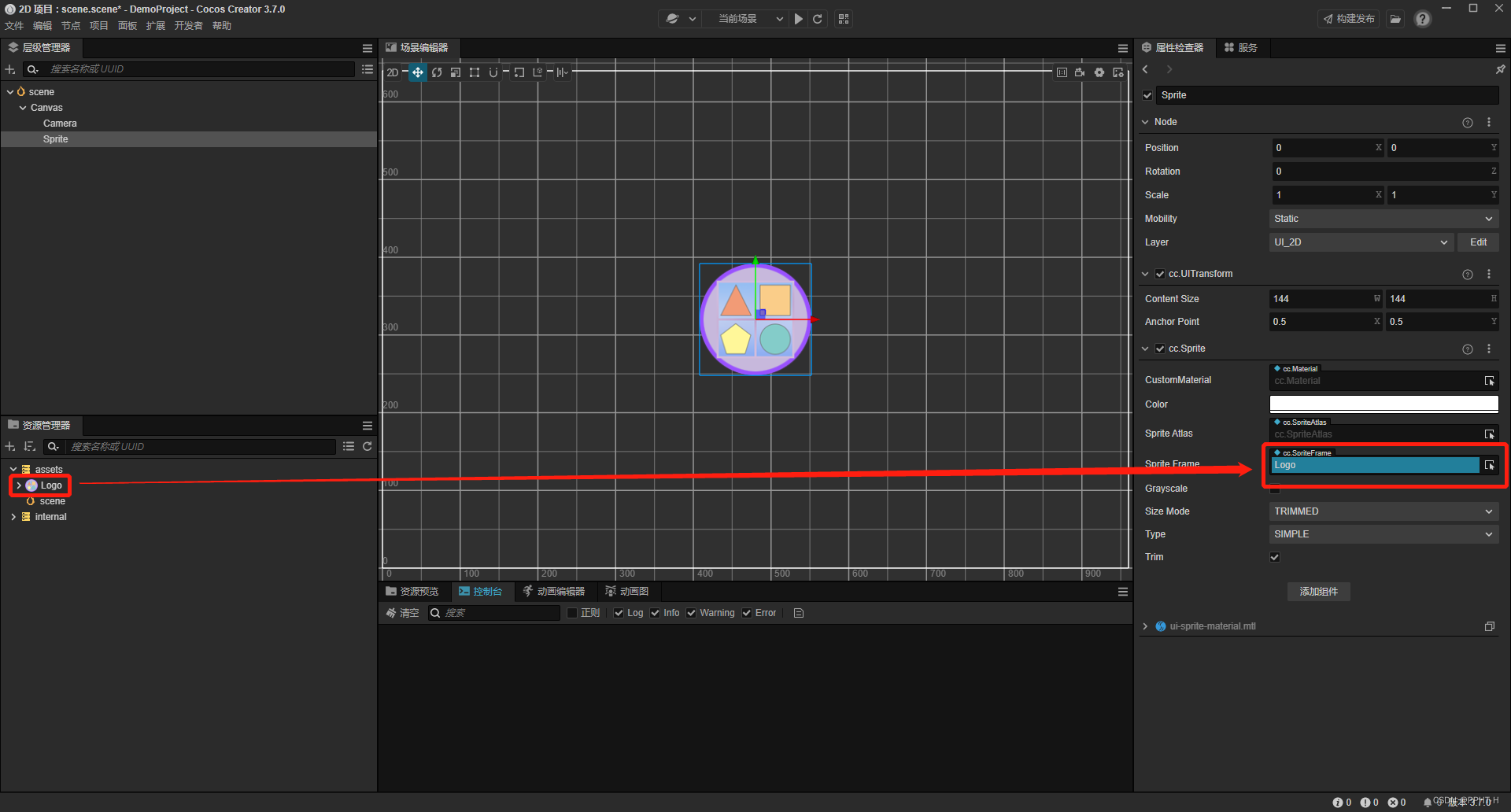
【微信小游戏开发笔记】第二节:Cocos开发界面常用功能简介
Cocos开发界面常用功能简介 本章只介绍微信小游戏开发时常用的功能,其他功能不常用,写多了记不住(其实是懒 -_-!): 层级管理器,用于操作各个节点。资源管理器,用于操作各种文件资源。场景编辑…...

3分钟,学会了一个调试CSS的小妙招
Ⅰ. 作用 用于调试CSS , 比控制台添更加方便,不需要寻找 ;边添加样式,边可以查看效果,适合初学者对CSS 的理解和学习; Ⅱ. 快速实现(两边) ① 显示这个样式眶 给 head 和 style 标签添加一个…...

【项目精选】基于jsp的健身俱乐部会员系统
点击下载源码 社会可行性 随着社会的发展和计算机技术的进步,人类越来越依赖于信息化的管理系统,这种系统能更加方便的获得信息以及处理信息。人们都改变了过去的思维,开始走向了互联网的时代,在 可行性小结 本章在技术可行性上…...

java注解
1. Java注解(Annotation) 2. Java注解分类 3. JDK基本注解 4. JDK元注解 5. 注解分类 6. 自定义注解开发 7. 提取Annotation信息 8. 注解处理器 9. 动态注解处理器(spring aop方式) 1. Java注解(Annotation) Java注解是附加在代码中的一些元信息,用于…...

移动测试相关
一、环境搭建 准备工作: (python、pycharm安装配置好) 1、Java SDK 安装配置 Java Downloads | Oracle 下载安装后配置系统环境变量:JAVA_HOME(jdk根目录路径)和path(jdk根目录下的bin目录路径…...
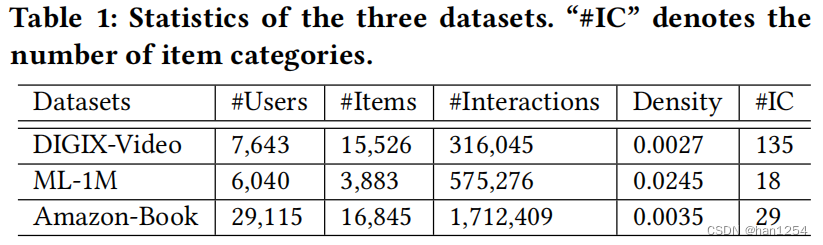
SIGIR22:User-controllable Recommendation Against Filter Bubbles
User-controllable Recommendation Against Filter Bubbles 摘要 推荐系统经常面临过滤气泡的问题:过度推荐基于用户特征以及历史交互的同质化项目。过滤气泡将会随着反馈循环增长,缩小了用户兴趣。现有的工作通常通过纳入诸如多样性和公平性等准确性之…...
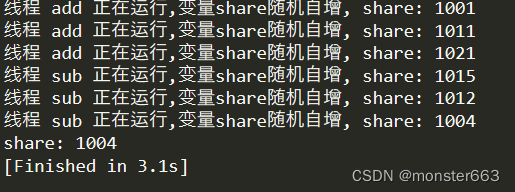
Python中的进程线程
文章目录前言多进程与多线程基本概念多进程multiprocessing 类对象进程池subprocess模块进程间通信多线程threading实现线程操作线程共享所有变量线程锁参考资料前言 又花了点时间学习了一下Python中的多线程与多进程的知识点,梳理一下供复习参考 多进程与多线程 …...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

shell脚本--常见案例
1、自动备份文件或目录 2、批量重命名文件 3、查找并删除指定名称的文件: 4、批量删除文件 5、查找并替换文件内容 6、批量创建文件 7、创建文件夹并移动文件 8、在文件夹中查找文件...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

VM虚拟机网络配置(ubuntu24桥接模式):配置静态IP
编辑-虚拟网络编辑器-更改设置 选择桥接模式,然后找到相应的网卡(可以查看自己本机的网络连接) windows连接的网络点击查看属性 编辑虚拟机设置更改网络配置,选择刚才配置的桥接模式 静态ip设置: 我用的ubuntu24桌…...

【Go语言基础【13】】函数、闭包、方法
文章目录 零、概述一、函数基础1、函数基础概念2、参数传递机制3、返回值特性3.1. 多返回值3.2. 命名返回值3.3. 错误处理 二、函数类型与高阶函数1. 函数类型定义2. 高阶函数(函数作为参数、返回值) 三、匿名函数与闭包1. 匿名函数(Lambda函…...

音视频——I2S 协议详解
I2S 协议详解 I2S (Inter-IC Sound) 协议是一种串行总线协议,专门用于在数字音频设备之间传输数字音频数据。它由飞利浦(Philips)公司开发,以其简单、高效和广泛的兼容性而闻名。 1. 信号线 I2S 协议通常使用三根或四根信号线&a…...
的使用)
Go 并发编程基础:通道(Channel)的使用
在 Go 中,Channel 是 Goroutine 之间通信的核心机制。它提供了一个线程安全的通信方式,用于在多个 Goroutine 之间传递数据,从而实现高效的并发编程。 本章将介绍 Channel 的基本概念、用法、缓冲、关闭机制以及 select 的使用。 一、Channel…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
