Python社会经济 | 怀特的异方差一致估计量
🎯要点
🎯算法和模型底层数学及代码:🖊线性代数应用(主成分分析):降维、投影(用于求解线性系统)和二次形式(用于优化)| 🖊奇值分解 | 🖊线性代数 | 🖊求方程根 | 🖊数值优化及算法 | 🖊梯度方向和牛顿方向的线搜索 | 🖊最小二乘优化 | 🖊梯度下降优化 | 🖊约束优化 | 🖊并行编程 | 🖊多核并行 | 🖊使用C/C++代码 | 🖊贝叶斯和概率规划 | 🖊蒙特卡罗方法 | 🖊蒙特卡罗积分 | 🖊马尔可夫链 | 🖊马尔可夫链蒙特卡罗 | 🖊哈密顿蒙特卡罗 | 🖊线性回归 | 🖊逻辑回归 | 🖊分层模型 | 🖊混合模型 | 🖊概率分布。
📜概率统计算法模型和并行计算-用例
📜Python产品价格弹性生命周期和客户群利润点概率推理数学模型 | 📜Python | MATLAB | R 心理认知数学图形模型推断 | 📜Python燃气轮机汽车钢棒整流电路控制图统计模型过程潜力分析 | 📜Python高层解雇和客户活跃度量化不确定性模型 | 📜Python | R 雌雄配对和鱼仔变异马尔可夫链 | 📜Julia和Python蛛网图轨道图庞加莱截面曲面确定性非线性系统 | 📜C++和Python通信引文道路社评电商大规模行为图结构数据模型 | 📜Python和C++数学物理计算分形热力学静电学和波动方程 | 📜C++和Python计算金融数学方程算法模型 | 📜Python和R概率统计算法建模评估气象和运动 | 📜Python流体数据统计模型和浅水渗流平流模型模拟 | 📜社会经济怀特的异方差一致估计量统计推理。
🍇Python统计可视化离群值
机器学习算法的成功在很大程度上取决于输入模型的数据的质量。现实世界的数据通常很脏,包含异常值、缺失值、错误的数据类型、不相关的特征或非标准化数据。任何这些因素的存在都会阻碍机器学习模型的正确学习。因此,将原始数据转换为有用的格式是机器学习过程中必不可少的阶段。
离群值是数据集中表现出某种异常并与正常数据有显著偏差的对象。在某些情况下,离群值可以提供有用的信息(例如在欺诈检测中)。然而,在其他情况下,它们不会提供任何有用的信息,并且会严重影响学习算法的性能。
在此,我们将演示使用箱线图、散点图和残差等多种技术从数据集中识别异常值。
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
plt.style.use('seaborn')# read csv file
df_weight = pd.read_csv('weight.csv')# visualize the first 5 rows
df_weight.head()
height weight 0 161.000724 55.530340 1 171.504245 71.872692 2 173.201739 69.897780 3 166.563658 62.395484 4 176.464080 80.540956 \begin{array}{rrr} & \text { height } & \text { weight } \\ \hline 0 & 161.000724 & 55.530340 \\ 1 & 171.504245 & 71.872692 \\ 2 & 173.201739 & 69.897780 \\ 3 & 166.563658 & 62.395484 \\ 4 & 176.464080 & 80.540956 \end{array} 01234 height 161.000724171.504245173.201739166.563658176.464080 weight 55.53034071.87269269.89778062.39548480.540956
您可能会注意到,本文使用的数据集非常简单(100 个观察值和 2 个特征)。在现实世界的问题中,您将处理更复杂的数据集。然而,识别异常值的程序保持不变
💦识别离群值
有许多视觉和统计方法来检测异常值。我们将详细解释 5 种用于识别数据集中异常值的工具:(1) 直方图,(2) 箱线图,(3) 散点图,(4) 残差值和 (5) Cook 距离。
直方图是可视化数值变量分布的常见图。在直方图中,数据被分成也称为区间的区间。每个条形的高度代表每个箱内数据点的频率。两个变量的直方图如下所示。条形图呈钟形曲线,表明两个特征(体重和身高)呈正态分布。此外,还描绘了高斯核密度估计函数。该函数是概率密度函数的近似值,表示连续变量落入特定值范围内的概率。
ax = sns.distplot(df_weight.height, hist=True, hist_kws={"edgecolor": 'w', "linewidth": 3}, kde_kws={"linewidth": 3})ax.annotate('Possible outlier', xy=(188,0.0030), xytext=(189,0.0070), fontsize=12,arrowprops=dict(arrowstyle='->', ec='grey', lw=2), bbox = dict(boxstyle="round", fc="0.8"))plt.xticks(fontsize=14)
plt.yticks(fontsize=14)plt.xlabel('height', fontsize=14)
plt.ylabel('frequency', fontsize=14)
plt.title('Distribution of height', fontsize=20);
(图略,请自行执行上述代码)
ax = sns.distplot(df_weight.weight, hist=True, hist_kws={"edgecolor": 'w', "linewidth": 3}, kde_kws={"linewidth": 3})ax.annotate('Possible outlier', xy=(102, 0.0020), xytext=(103, 0.0050), fontsize=12,arrowprops=dict(arrowstyle='->', ec='grey', lw=2), bbox=dict(boxstyle="round", fc="0.8"))plt.xticks(fontsize=14)
plt.yticks(fontsize=14)plt.xlabel('weight', fontsize=14)
plt.ylabel('frequency', fontsize=14)
plt.title('Distribution of weights', fontsize=20);
(图略,请自行执行上述代码)
如上所示,两个变量似乎都存在异常值(孤立条)。重要的是要记住,直方图不能像箱线图那样从统计上识别异常值。相反,使用直方图识别异常值完全是视觉上的,取决于我们的个人观点。
箱线图是探索性数据分析的绝佳工具,可以轻松地在分布之间进行比较。它显示了数据集的五数摘要,其中包括:
- 最小值:排除异常值后的最小值(根据IQR邻近规则计算)
- 最大值:排除异常值后的最大值(根据IQR邻近规则计算)
- 中位数 (Q2):分布的中点
- 第一个四分位数(Q1):数据集下半部分的中点
- 第三四分位数(Q3):数据集上半部分的中点
方框表示第一四分位数和第三四分位数之间的数据,也称为四分位距 (IQR = Q3-Q1)。它包含 50% 的数据,并被中位数分成两部分。须根据 IQR 接近规则表示。
上边界 = = = 第三个四分位数 + ( 1.5 +(1.5 +(1.5 *QR ) ) )
下边界 = = = 第一个四分位数 − ( 1. 5 ∗ I Q R ) -\left(1.5^* IQR \right) −(1.5∗IQR)
如果某个值超出此范围,则该值被视为离群值,并以带点的箱线图表示。
两个变量的箱线图如下所示。我们在身高 = 190 和体重 = 105 处观察到异常值。
ax = sns.boxplot(df_weight.height)ax.annotate('Outlier', xy=(190,0), xytext=(186,-0.05), fontsize=14,arrowprops=dict(arrowstyle='->', ec='grey', lw=2), bbox = dict(boxstyle="round", fc="0.8"))plt.xticks(fontsize=14)
plt.xlabel('height', fontsize=14)
plt.title('Distribution of height', fontsize=20)
ax = sns.boxplot(df_weight.weight)ax.annotate('Outlier', xy=(105,0), xytext=(98,-0.05), fontsize=14,arrowprops=dict(arrowstyle='->', ec='grey', lw=2), bbox = dict(boxstyle="round", fc="0.8"))plt.xticks(fontsize=14)
plt.xlabel('weight', fontsize=14)
plt.title('Distribution of weight', fontsize=20)
与直方图不同,箱线图根据 IQR 邻近规则统计识别异常值,这意味着异常值的识别不仅仅依赖于我们的个人观点。
👉参阅一:计算思维
👉参阅二:亚图跨际
相关文章:

Python社会经济 | 怀特的异方差一致估计量
🎯要点 🎯算法和模型底层数学及代码:🖊线性代数应用(主成分分析):降维、投影(用于求解线性系统)和二次形式(用于优化)| 🖊奇值分解…...

《被讨厌的勇气》笔记
自由就是被别人讨厌。对人而言,最大的不幸就是不喜欢自己。活在“如果怎样怎样”之类的假设之中,就根本无法改变。活在害怕关系破裂的恐惧之中,那是为他人而活的一种不自由的生活方式。人生是连续刹那,我们只能活在“此时此刻”。…...

Python爬虫协程批量下载图片
import aiofiles import aiohttp import asyncio import requests from lxml import etree from aiohttp import TCPConnectorclass Spider:def __init__(self, value):# 起始urlself.start_url value# 下载单个图片staticmethodasync def download_one(url):name url[0].spl…...

Flask Web开发基础:数据库与ORM实战
Flask Web开发基础:数据库与ORM实战 该文介绍了如何使用 Flask、SQLAlchemy 和 SQLite 实现数据库操作。首先,通过创建虚拟环境和安装 flask-sqlalchemy(版本2.5.1)及 sqlalchemy(版本1.4.47)来设置环境。接…...

pidstat -d 1分析磁盘吞吐量
iostat -dx 1 查看磁盘IO吞吐量 pidstat -d 1看是哪个进程写的...

期望20K,2年golang深圳某互联网小公司一面
后续约了二面(CTO面),需要到现场,基本没问啥具体的技术知识,都是聊规划和个人职业目标 一面 1、假设访问百度网站,从在浏览器输入网址,到最终页面展示出来,中间会发生哪些事情&…...
#02 安装指南:如何配置Stable Diffusion环境
文章目录 前言前置条件第1步:安装Python和PIP第2步:创建虚拟环境第3步:安装PyTorch和CUDA第4步:安装Stable Diffusion相关库第5步:测试环境结论 前言 在之前的文章中,我们介绍了Stable Diffusion基础入门和…...

拼多多笔试
拼多多2022数据分析笔试(0822) 一、选择题 1.已知样本量n,样本均值及方差求置信区间 2.决策树 3.峰度系数 4.协方差 5.第一、第二熵变 6.充分统计量 7.xgboost 8.方差分析中的多重比较 二、编程题 1. 一张用户点击路径的表&#x…...
Golang | Leetcode Golang题解之第119题杨辉三角II
题目: 题解: func getRow(rowIndex int) []int {row : make([]int, rowIndex1)row[0] 1for i : 1; i < rowIndex; i {row[i] row[i-1] * (rowIndex - i 1) / i}return row }...

Flutter 中的 SliverIgnorePointer 小部件:全面指南
Flutter 中的 SliverIgnorePointer 小部件:全面指南 Flutter 是一个由 Google 开发的跨平台 UI 框架,它提供了一系列的组件来帮助开发者构建高性能、美观的移动、Web 和桌面应用。在 Flutter 的滚动组件中,SliverIgnorePointer 是一个用来包…...

比较两台计算机上的LabVIEW、工具包及驱动程序的一致性
比较两台计算机上的LabVIEW、工具包及驱动程序是否相同,可以通过以下步骤实现: 1. 检查LabVIEW版本 方法一:在LabVIEW中查看版本信息 步骤: 打开LabVIEW。点击菜单栏的 Help > About LabVIEW。记录显示的LabVIEW版本号和许可…...

参考——温湿度传感器DHT11驱动_STM32
设备:stm32f407ZGT6 环境:FreeRTOS HAL 到网上找DHT11的驱动,但是都无法使用。原因是RTOS环境中,由于多线程,使用循环计数阻塞式的delay_us延时函数就没那么准,且不同设备中delay_us的计数值不一样…...

架构每日一学 14:架构师如何进行可行性探索?
架构活动中,如果不进行可行性探索可能会导致重大失误,为企业发展带来风险。 可行性探索是架构活动的最后一个节点,在这之后的架构活动就像是离弦之箭,即便发现重大风险也很难再回头了。 互联网公司之间的竞争非常激烈࿰…...

多线程知识-13
为什么应该在循环中检查等待条件 为了实现多线程的同步和协调,通常使用等待和唤醒机制。在等待和唤醒机制中,等待条件是指一个线程等待某个条件的满足,当条件满足时,线程被唤醒继续执行。 在循环中检查等待条件的目的是为了避免虚…...

vue3+cli-service配置代理,跨域请求
一、配置代理端口和代理转发 在vue.config.js文件中 const {defineConfig} require(vue/cli-service)module.exports defineConfig({devServer: {host: 0.0.0.0,port: 8088, // 启动端口号proxy: {/api: { // 请求接口中要替换的标识target: , // 代理地址,后…...

git介绍、安装、配置
文章目录 1. GIT介绍2. 使用GIT的好处3. GIT 安装4. GIT 配置4.1 GIT 初始化设置、命令别名设置4.2 如果终端安装了oh-my-zsh,会带一堆git命令别名4.3 GIT配置文件介绍4.3.1 Linux、Mac OS系统4.3.2 windows系统 5. git设置远程仓库账号密码(拉取、上传代码不用输入…...

打开flutter调试
debugPaintSizeEnabled true; debugPaintBaselinesEnabled true;...

【前端 - Vue】Vuex基础入门,创建仓库的详细步骤
🚀 个人简介:6年开发经验,现任职某国企前端负责人,分享前端相关技术与工作常见问题~ 💟 作 者:前端菜鸟的自我修养❣️ 📝 专 栏:vue从基础到起飞 🌈 若有帮助&…...

#01 Stable Diffusion基础入门:了解AI图像生成
文章目录 前言什么是Stable Diffusion?Stable Diffusion的工作原理如何使用Stable Diffusion?Stable Diffusion的应用场景结论 前言 在当今迅速发展的人工智能领域,AI图像生成技术以其独特的魅力吸引了广泛的关注。Stable Diffusion作为其中的一项前沿技术&#…...
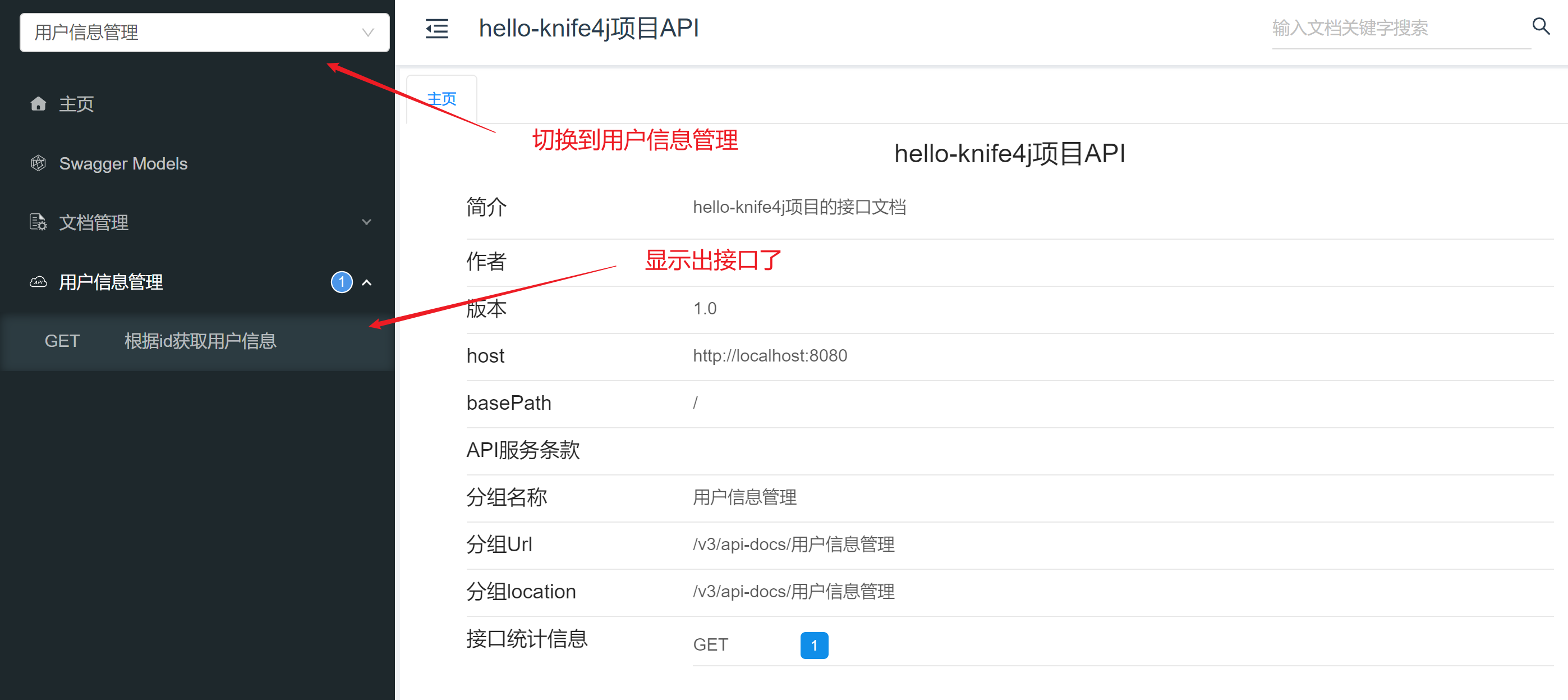
Knife4j使用
Knife4j使用 文章目录 Knife4j使用1、Knife4j介绍2、SpringBoot集成Knife4j3、基本使用 1、Knife4j介绍 Knife4j是一个用于生成和展示API文档的工具,同时它还提供了在线调试的功能,可以看作是Swagger的升级版,界面也比Swagger更好看…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...
