Scikit-Learn随机森林回归
Scikit-Learn随机森林回归
- 1、随机森林
- 1.1、集成学习
- 1.2、Bagging方法
- 1.3、随机森林算法
- 1.4、随机森林的优缺点
- 2、Scikit-Learn随机森林回归
- 2.1、Scikit-Learn随机森林回归API
- 2.2、随机森林回归实践(加州房价预测)
1、随机森林
随机森林是一种由决策树构成的集成算法,它在大多情况下都能有不错的表现。随机森林既可用于回归也可用于分类。随机森林回归在机器学习知识结构中的位置如下:

1.1、集成学习
随机森林是一种由决策树构成的(并行)集成算法,属于Bagging类型,随机森林通过组合多个弱分类器,最终结果通过投票或取均值,使得整体模型的结果具有较高的精确度和泛化性能,同时也有很好的稳定性,因此广泛应用在各种业务场景中
随机森林有如此优良的表现,主要归功于随机和森林。顾名思义,随机森林是一个比喻,它由若干决策树构成,每棵决策树都是其基本单元。至于随机,只是一个数学抽样概念。随机使它具有抗过拟合能力,森林使它更加精准
关于决策树的介绍详见文章:回归树 和 决策树
随机森林的基本思想在于集思广益,集中群众的智慧,广泛吸收有益的意见。这往往可以得到更好的解决方案。集思广益在机器学习中对应一个关键概念——集成学习
集成学习(Ensemble Learning)通过训练学习多个个体学习器,当预测时通过结合策略将多个个体学习器的结果组合作为最终强学习器的结果输出
对于训练数据集,我们训练一系列个体学习器,再通过结合策略将它们集成起来,形成一个更强的学习器,这就是集成学习所做的事情

其中,个体学习器是相对于集成学习来说的,其实我们在之前了解到的很多模型,例如决策树算法、朴素贝叶斯算法等,都是个体学习器
而集成可以分为同质集成和异质集成:
- 同质集成:只包含同种类型的个体学习器,个体学习器称作基学习器。例如随机森林中全是决策树集成
- 异质集成:包含不同类型的个体学习器,个体学习器称作组件学习器。例如同时包含决策树和神经网络进行集成
个体学习器代表的是单个学习器,集成学习代表的是多个学习器的结合
集成学习的核心问题有两个:
- 使用什么样的个体学习器?
- 准确性:个体学习器不能太弱,需要有一定的准确性
- 多样性:个体学习器之间要存在差异性,即具有多样性
- 如何选择合适的结合策略构建强学习器?
- 并行组合方式:例如随机森林
- 传统组合方式:例如Boosting树模型
1.2、Bagging方法
这里我们只讲随机森林的并行集成模型,而Bagging是并行式集成学习方法最著名的代表
Bagging方法全称为自助聚集(Bootstrap Aggregating),顾名思义,Bagging由Bootstrap与Aggregating两部分组成
要理解Bagging,首先要了解自助采样法(Bootstrap Sampling)

自助采样的过程为
- 给定包含m个样本的数据集,先随机取出一个样本放入采样集中,再把该样本放回初始数据集,使得下次采样时该样本仍有可能被选中
- 重复上述过程m轮,得到包含m个样本的采样集,初始数据集中有的样本在采样集中多次出现,有的则从未出现
- 假设约63.2%的样本出现在采样集中,而未出现的约36.8%的样本可用作验证集来对后续的泛化性能进行包外/袋外估计
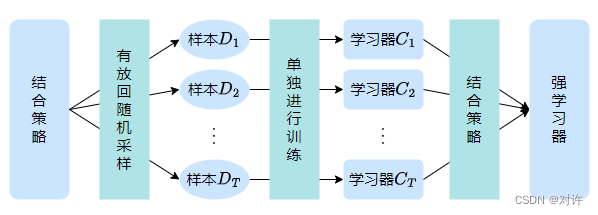
Bagging方法是在自助采样基础上构建的,上述的采样过程我们可以重复T次,采样出T个包含m个样本的采样集,然后基于每个采样集训练出一个基学习器,然后将这些基学习器进行结合
在对预测输出进行结合时,Bagging通常对分类任务使用简单投票法,对回归任务使用简单平均法,这就是Bagging方法的基本流程
从偏差-方差分解的角度看,Bagging主要关注降低方差,因此它在不剪枝的决策树、神经网络等易受到样本扰动的学习器上效用更明显
1.3、随机森林算法
随机森林(Random Forest,RF)是一种基于树模型的Bagging的优化版本。核心思想依旧是Bagging,但是做了一些独特的改进——RF使用了CART决策树作为基学习器。具体过程如下:
- 输入样本集 D D D= { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x m , y m ) } \{{ (x_1,y_1),(x_2,y_2),...,(x_m,y_m) \}} {(x1
相关文章:

Scikit-Learn随机森林回归
Scikit-Learn随机森林回归 1、随机森林1.1、集成学习1.2、Bagging方法1.3、随机森林算法1.4、随机森林的优缺点2、Scikit-Learn随机森林回归2.1、Scikit-Learn随机森林回归API2.2、随机森林回归实践(加州房价预测)1、随机森林 随机森林是一种由决策树构成的集成算法,它在大多…...

Vue Router 教程
Vue Router 是 Vue.js 的官方路由管理器,它提供了一种方便的方式来管理应用的路由。在本教程中,我们将介绍 Vue Router 的一些常见用法和示例。 一、安装 Vue Router 使用 Vue Router 之前,需要先安装它。可以使用以下命令通过 npm 安装&am…...
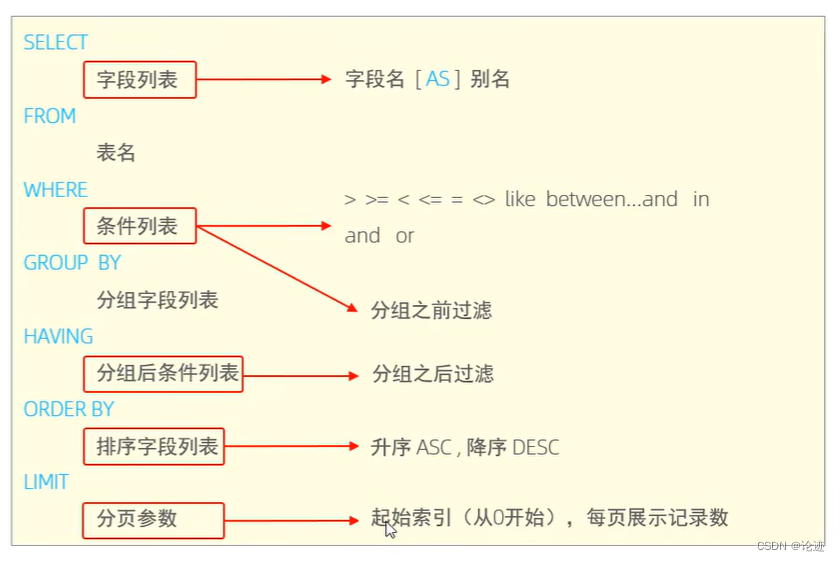
【数据库】SQL--DQL(初阶)
文章目录 DCL1. 基本介绍2. 语法2.1 基础查询2.2 条件查询2.3 聚合函数2.4 聚合查询2.5 分组查询2.6 排序查询2.7 分页查询2.8 综合案例练习2.9 执行顺序 3. DQL总结 DCL 更多数据库MySQL系统内容就在以下专栏: 专栏链接:数据库MySQL 1. 基本介绍 DQL英…...
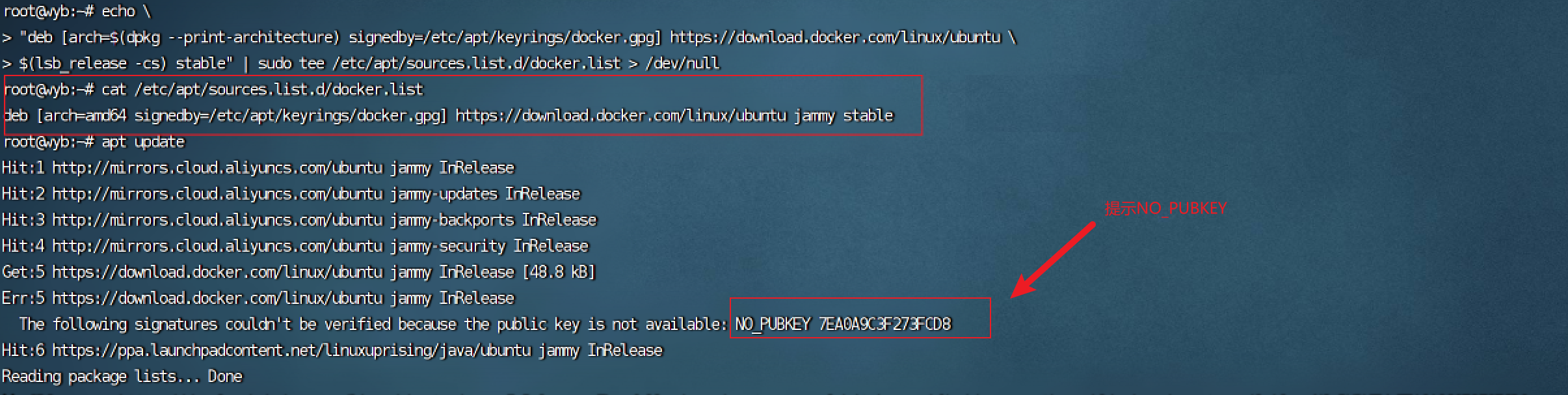
【docker】docker的安装
如果之前安装了旧版本的docker我们需要进行卸载: 卸载之前的旧版本 卸载 # 卸载旧版本 sudo apt-get remove docker docker-engine docker.io containerd runc # 卸载历史版本 apt-get purge docker-ce docker-ce-cli containerd.io docker-buildx-plugin docker…...
OC IOS 文件解压缩预览
热很。。热很。。。。夏天的城市只有热浪没有情怀。。。 来吧,come on。。。 引用第三方库: pod SSZipArchive 开发实现: 一、控制器实现 头文件控制器定义: // // ZipRarViewController.h // // Created by carbonzhao on 2…...

python-web应用程序-Django-From组件
python-web应用程序-Django-From组件 添加用户时 原始方法(本质)【麻烦】 def user_add(req):if req.method GET:return render(req,XXX.html)#POST请求处理:XXXXX-用户数据没有校验 -出现错误提示 -页面上的每一个字段都需要我们重新写一遍 -关联数…...

K8s(Kubernetes)常用命令
大家好,当谈及容器编排工具时,Kubernetes(常简称为K8s)无疑是当今最受欢迎和广泛使用的解决方案之一。作为一个开源的容器编排平台,Kubernetes 提供了丰富的功能,可以帮助开发人员和运维团队管理、部署和扩…...

C#-for循环语句
for循环语句 语法: for(初始化变量; 判断条件; 增量表达式) { // 内部代码 } 第一个空(初始表达式): 一般用来声明一个临时的局部变量 用来计数第二个空(条件表达式): 表明进入循环的条件 一个bool类型的值(bool类型 条件表达式 逻辑运算符)第三个空(增量表达式): 使用第一个空…...

css动画案例练习之会展开的魔方和交错的小块
这里写目录标题 一级目录二级目录三级目录 下面开始案例的练习,建议第一个动手操作好了再进行下一个一、交错的小块效果展示1.大致思路1.基本结构2.实现动态移动 2.最终版代码 二、会展开的魔方1.大致思路1.基本结构;2.静态魔方的构建3.让静态的魔方动起来 2.最终版…...
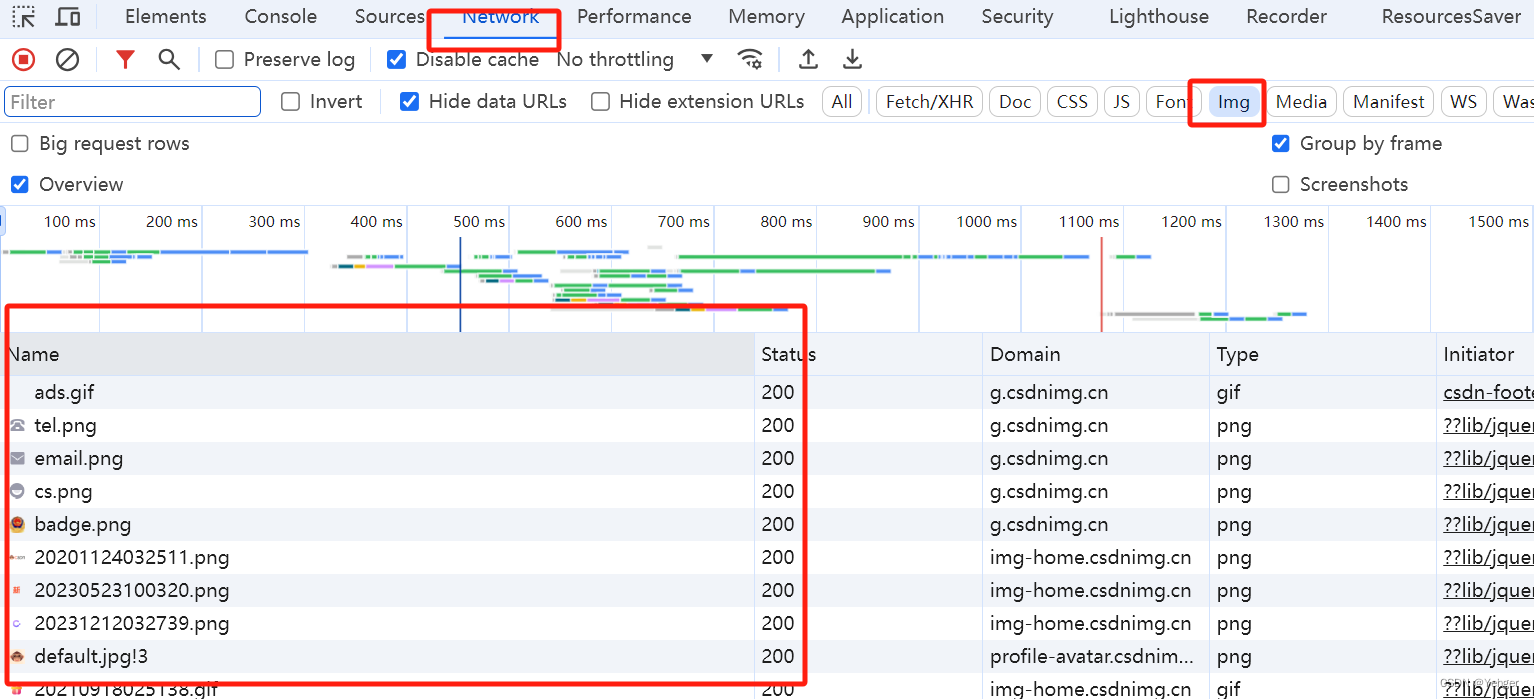
前端逆向之下载canvas引用的图片
前端逆向之下载canvas引用的图片 一、来源二、解决三、如果在Network这里也找不到呢? 一、来源 当我们用dom检查器的时候无法选中想要扒下来的图片,只能选中canvas,这种时候该怎么办呢? 二、解决 这个时候应该换个脑子…...

深度学习手撕代码题
目录: PyTorch实现注意力机制、多头注意力与自注意力Numpy广播机制实现矩阵间L2距离的计算Conv2D卷积的Python和C++实现Numpy实现bbox_iou的计算Numpy实现FocallossPython实现nms、softnmsPython实现BN批量归一化PyTorch卷积与BatchNorm的融合分割网络损失函数Dice Loss代码实…...
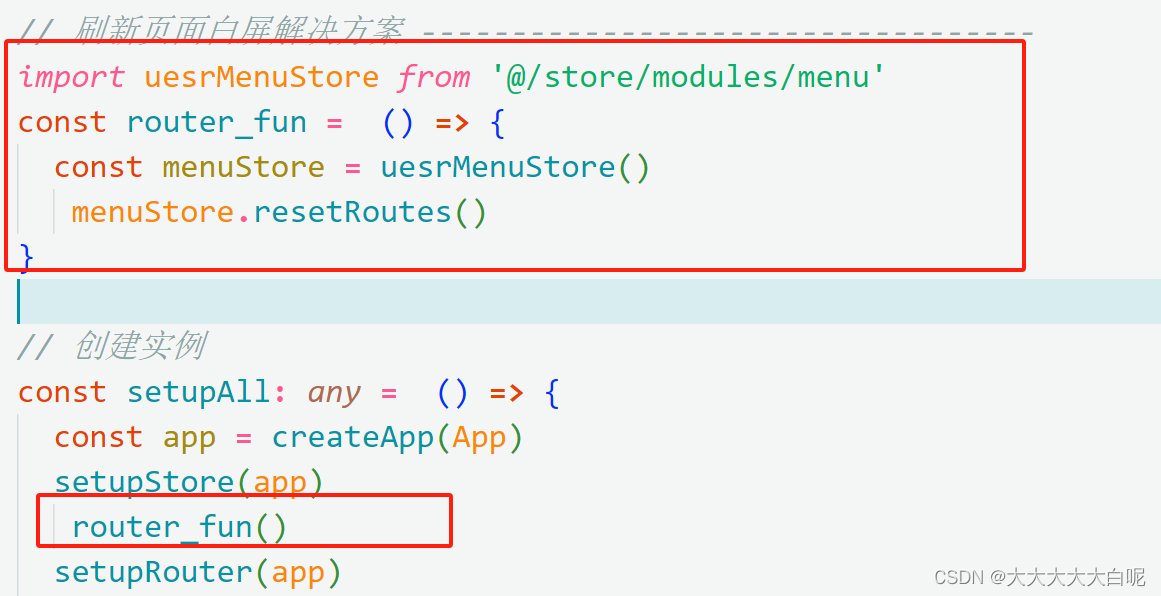
vue3 + ts 动态添加路由,刷新页面白屏问题解决方案
1、store 中添加路由的方法 2、main.ts中使用该方法 然后就可以任意刷新页面了,有问题可以随时滴我...........

【Kubernetes】k8s的调度约束(亲和与反亲和)
一、调度约束 list-watch 组件 Kubernetes 是通过 List-Watch 的机制进行每个组件的协作,保持数据同步的,每个组件之间的设计实现了解耦。 用户是通过 kubectl 根据配置文件,向 APIServer 发送命令,在 Node 节点上面建立 Pod 和…...

Java数据结构- Map和Set
目录 1. Map和Set2. Map的使用3. Set的使用 1. Map和Set Java中,Map和Set是两个接口,TreeSet、HashSet这两个类实现了Set接口,TreeMap、HashMap这两个类实现了Map接口。 带Tree的这两个类(TreeSet、TreeMap)底层的数…...
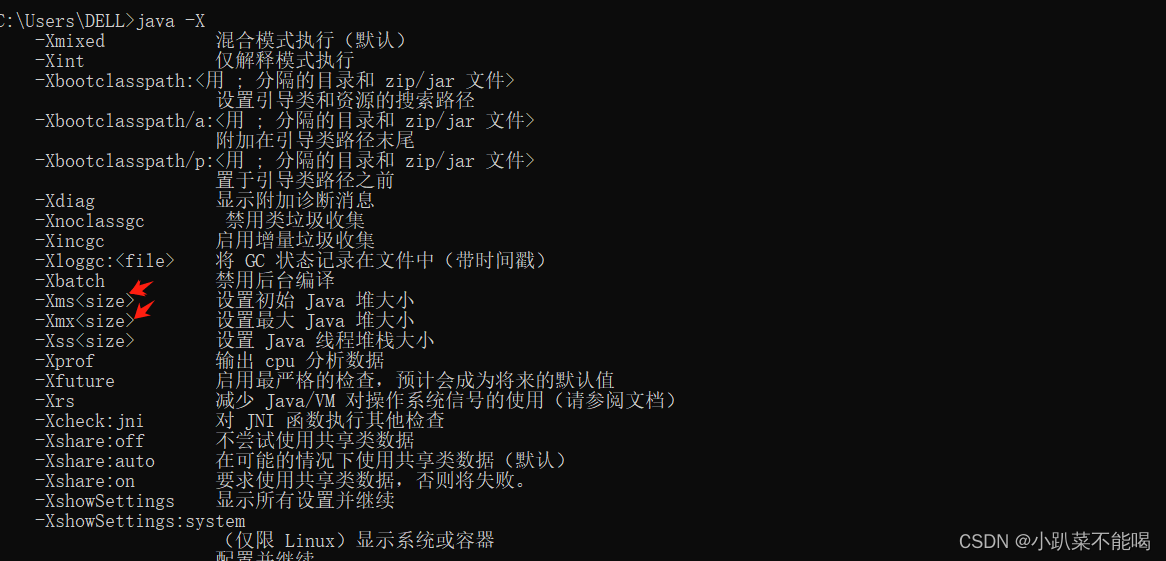
JVM参数配置
JVM参数的三种表示方法 在jvm中,jvm虚拟机参数有以下三种表示方法: 标准参数(-)所有的JVM实现都必须实现这些参数的功能,而且向后兼容非标准参数(-X),默认jvm实现这些参数的功能&…...

Vue 实现的精彩动画效果
在 Vue 开发中,我们可以利用<transition>组件来打造各种令人惊艳的动画效果。下面来详细看看这些有趣的动画效果及其实现代码。 一、缩放类效果 zoom-in(整体放大进入) <template><div><button click"isShow ! …...
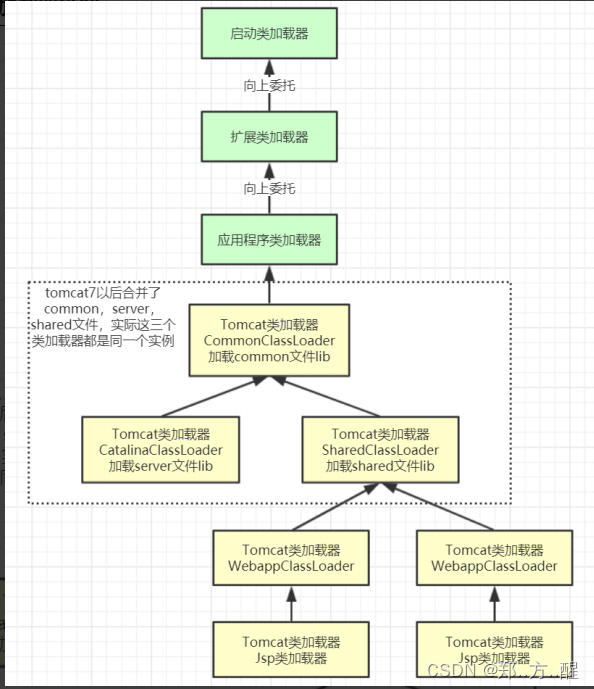
JVM类加载机制详解(JDK源码级别)
提示:从JDK源码级别彻底剖析JVM类加载机制、双亲委派机制、全盘负责委托机制、打破双亲委派机制的程序、Tomcat打破双亲委派机制、tomcat自定义类加载器详解、tomcat的几个主要类加载器、手写tomcat类加载器 文章目录 前言一、loadClass的类加载大概有如下步骤二、j…...

美国年轻人热衷床上“摆烂”,沃尔玛发掘床上用品新商机!
美国年轻人近年来热衷于床上“摆烂”生活方式,这反映了他们对舒适放松的追求和现代生活的压力。沃尔玛作为零售业巨头,敏锐地捕捉到这一市场变化,发现了床上用品的新商机。 美国年轻人忙碌中渴望宁静空间。床成为他们放松、逃离现实压力的理想…...

3168. 候诊室中的最少椅子数
给你一个字符串 s,模拟每秒钟的事件 i: 如果 s[i] E,表示有一位顾客进入候诊室并占用一把椅子。如果 s[i] L,表示有一位顾客离开候诊室,从而释放一把椅子。 返回保证每位进入候诊室的顾客都能有椅子坐的 最少 椅子…...
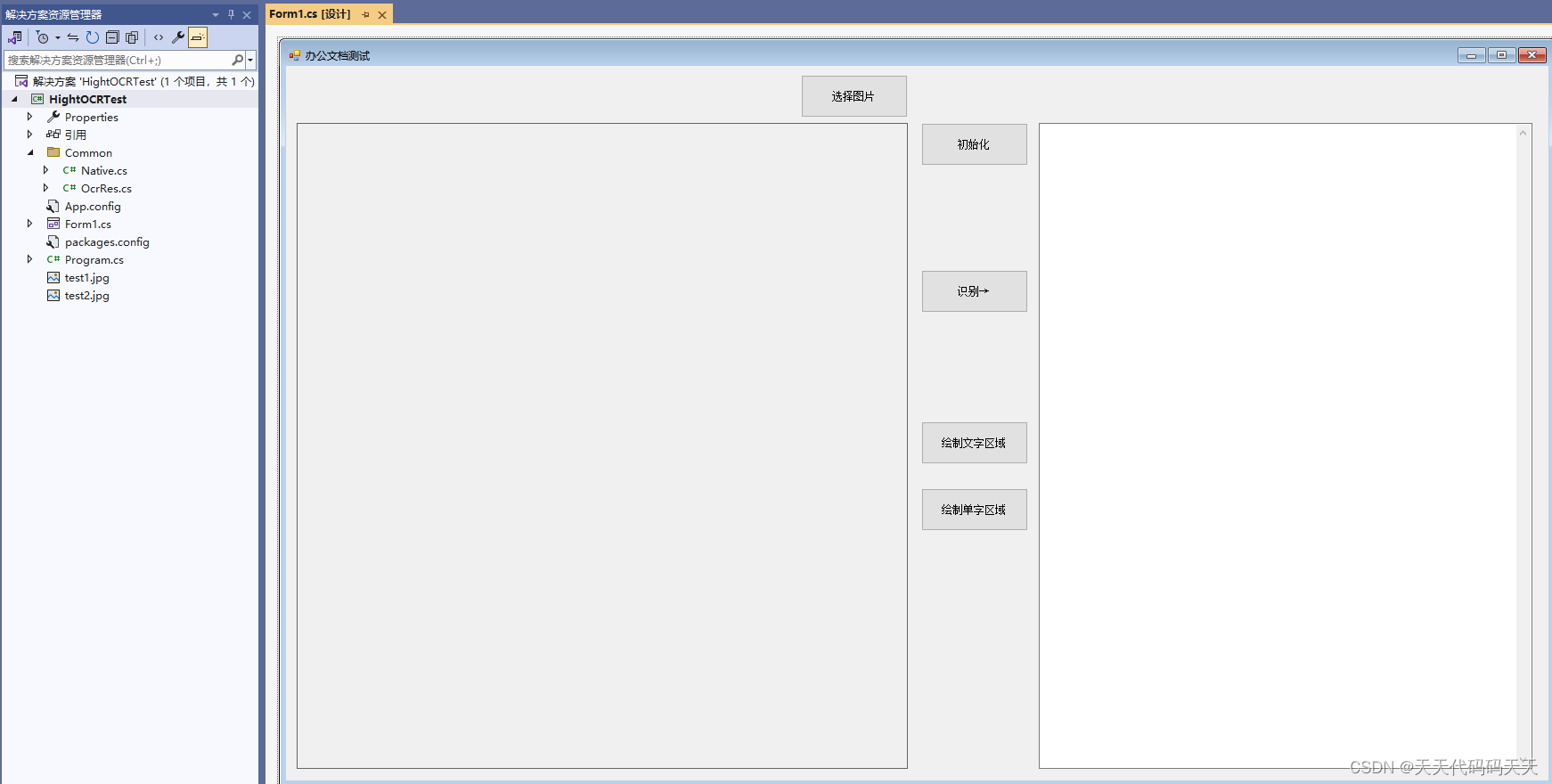
C# PaddleOCR 单字识别效果
C# PaddleOCR 单字识别效果 效果 说明 根据《百度办公文档识别C离线SDKV1.2用户接入文档.pdf》,使用C封装DLL,C#调用。 背景 为使客户、第三方开发者等能够更快速、方便的接入使用百度办公文档识别 SDK、促进百度 OCR产品赋能更多客户,特设…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...
