Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization)
Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization)
flyfish
目录
- Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization)
- 先看LayerNorm和BatchNorm
- 举个例子计算 LayerNorm
- RMSNorm 的整个计算过程
- 实际代码实现
- 结果
先看LayerNorm和BatchNorm
展示计算的方向

- axis=0 代表第一个轴,逐列处理数据。
- axis=1 代表第二个轴,逐行处理数据。在二维数组中,axis=-1 等同于 axis=1。
- axis=-1 代表最后一个轴。在二维数组中,axis=-1 等同于 axis=1,即最后一个轴。
在二维的情况 下,BatchNorm是按列算,LayerNorm按行算
import numpy as np
import matplotlib.pyplot as plt
import torch
import torch.nn as nnclass CustomLayerNorm:def __init__(self, eps=1e-5):self.eps = epsdef __call__(self, x):mean = np.mean(x, axis=-1, keepdims=True)std = np.std(x, axis=-1, keepdims=True)normalized = (x - mean) / (std + self.eps)return normalizedclass CustomBatchNorm:def __init__(self, eps=1e-5):self.eps = epsdef __call__(self, x):mean = np.mean(x, axis=0)std = np.std(x, axis=0)normalized = (x - mean) / (std + self.eps)return normalized# Original Data
data = np.array([[1.0, 2.0, 3.0],[4.0, 5.0, 6.0],[7.0, 8.0, 9.0]])# Apply Custom LayerNorm
custom_layer_norm = CustomLayerNorm()
custom_layer_norm_data = custom_layer_norm(data)# Apply Custom BatchNorm
custom_batch_norm = CustomBatchNorm()
custom_batch_norm_data = custom_batch_norm(data)# Apply PyTorch LayerNorm
data_tensor = torch.tensor(data, dtype=torch.float32)
layer_norm = nn.LayerNorm(data_tensor.size()[1:])
pytorch_layer_norm_data = layer_norm(data_tensor).detach().numpy()# Compare Custom and PyTorch LayerNorm
print("Original Data:\n", data)
print("Custom LayerNorm Data:\n", custom_layer_norm_data)
print("PyTorch LayerNorm Data:\n", pytorch_layer_norm_data)
Original Data:[[1. 2. 3.][4. 5. 6.][7. 8. 9.]]
Custom LayerNorm Data:[[-1.22472987 0. 1.22472987][-1.22472987 0. 1.22472987][-1.22472987 0. 1.22472987]]
PyTorch LayerNorm Data:[[-1.2247356 0. 1.2247356][-1.2247356 0. 1.2247356][-1.2247356 0. 1.2247356]]
举个例子计算 LayerNorm
具体步骤如下:
- 计算每行的均值:
- 对每一行,计算其均值。
- 第1行: mean = (1 + 2 + 3) / 3 = 2
- 第2行: mean = (4 + 5 + 6) / 3 = 5
- 第3行: mean = (7 + 8 + 9) / 3 = 8
- 计算每行的标准差:
- 对每一行,计算其标准差。
- 第1行: s t d = s q r t ( ( ( 1 − 2 ) 2 + ( 2 − 2 ) 2 + ( 3 − 2 ) 2 ) / 3 ) = s q r t ( ( 1 + 0 + 1 ) / 3 ) = s q r t ( 2 / 3 ) ≈ 0.8165 std = sqrt(((1-2)^2 + (2-2)^2 + (3-2)^2) / 3) = sqrt((1 + 0 + 1) / 3) = sqrt(2 / 3) ≈ 0.8165 std=sqrt(((1−2)2+(2−2)2+(3−2)2)/3)=sqrt((1+0+1)/3)=sqrt(2/3)≈0.8165
- 第2行: s t d = s q r t ( ( ( 4 − 5 ) 2 + ( 5 − 5 ) 2 + ( 6 − 5 ) 2 ) / 3 ) = s q r t ( ( 1 + 0 + 1 ) / 3 ) = s q r t ( 2 / 3 ) ≈ 0.8165 std = sqrt(((4-5)^2 + (5-5)^2 + (6-5)^2) / 3) = sqrt((1 + 0 + 1) / 3) = sqrt(2 / 3) ≈ 0.8165 std=sqrt(((4−5)2+(5−5)2+(6−5)2)/3)=sqrt((1+0+1)/3)=sqrt(2/3)≈0.8165
- 第3行: s t d = s q r t ( ( ( 7 − 8 ) 2 + ( 8 − 8 ) 2 + ( 9 − 8 ) 2 ) / 3 ) = s q r t ( ( 1 + 0 + 1 ) / 3 ) = s q r t ( 2 / 3 ) ≈ 0.8165 std = sqrt(((7-8)^2 + (8-8)^2 + (9-8)^2) / 3) = sqrt((1 + 0 + 1) / 3) = sqrt(2 / 3) ≈ 0.8165 std=sqrt(((7−8)2+(8−8)2+(9−8)2)/3)=sqrt((1+0+1)/3)=sqrt(2/3)≈0.8165
- 标准化每一行:
- 对每一行,使用均值和标准差进行标准化。公式为: ( x − m e a n ) / ( s t d + e p s ) (x - mean) / (std + eps) (x−mean)/(std+eps)。其中 eps 是一个小常数,防止除零,通常取值为 1e-5。
- 计算结果如下:
标准化公式: n o r m a l i z e d = ( x − m e a n ) / ( s t d + e p s ) normalized = (x - mean) / (std + eps) normalized=(x−mean)/(std+eps)
第1行:
[(1-2)/(0.8165+1e-5), (2-2)/(0.8165+1e-5), (3-2)/(0.8165+1e-5)]
= [-1.2247, 0, 1.2247]第2行:
[(4-5)/(0.8165+1e-5), (5-5)/(0.8165+1e-5), (6-5)/(0.8165+1e-5)]
= [-1.2247, 0, 1.2247]第3行:
[(7-8)/(0.8165+1e-5), (8-8)/(0.8165+1e-5), (9-8)/(0.8165+1e-5)]
= [-1.2247, 0, 1.2247]
最终标准化结果矩阵为:
[[-1.2247, 0, 1.2247][-1.2247, 0, 1.2247][-1.2247, 0, 1.2247]]
RMSNorm 的整个计算过程
Meta Llama 3 使用了RMSNorm
假设我们有以下 2D 输入张量 X X X(为了简单起见,我们假设这个张量有 2 行 3 列):
[ 1 2 3 4 5 6 ] \begin{bmatrix}1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} [142536]
RMSNorm 的计算过程如下:
- 计算每行的均方根 (RMS):
首先,对于每一行,我们计算该行元素的平方和的均值,然后取其平方根。
对于第 1 行:
RMS row1 = 1 2 + 2 2 + 3 2 3 = 1 + 4 + 9 3 = 4.67 ≈ 2.16 \text{RMS}_{\text{row1}} = \sqrt{\frac{1^2 + 2^2 + 3^2}{3}} = \sqrt{\frac{1 + 4 + 9}{3}} = \sqrt{4.67} \approx 2.16 RMSrow1=312+22+32=31+4+9=4.67≈2.16
对于第 2 行:
RMS row2 = 4 2 + 5 2 + 6 2 3 = 16 + 25 + 36 3 = 25.67 ≈ 5.07 \text{RMS}_{\text{row2}} = \sqrt{\frac{4^2 + 5^2 + 6^2}{3}} = \sqrt{\frac{16 + 25 + 36}{3}} = \sqrt{25.67} \approx 5.07 RMSrow2=342+52+62=316+25+36=25.67≈5.07 - 使用均方根对输入进行归一化:
将每行的元素除以该行的 RMS 值。这里的 epsilon 用于防止除以零的问题,我们假设 ϵ = 1 e − 6 \epsilon = 1e-6 ϵ=1e−6。
对于第 1 行: Normed row1 = [ 1 2.16 + ϵ 2 2.16 + ϵ 3 2.16 + ϵ ] ≈ [ 0.462 0.925 1.387 ] \text{Normed}_{\text{row1}} = \begin{bmatrix} \frac{1}{2.16 + \epsilon} & \frac{2}{2.16 + \epsilon} & \frac{3}{2.16 + \epsilon} \end{bmatrix} \approx \begin{bmatrix} 0.462 & 0.925 & 1.387 \end{bmatrix} Normedrow1=[2.16+ϵ12.16+ϵ22.16+ϵ3]≈[0.4620.9251.387]
对于第 2 行: Normed row2 = [ 4 5.07 + ϵ 5 5.07 + ϵ 6 5.07 + ϵ ] ≈ [ 0.789 0.986 1.183 ] \text{Normed}_{\text{row2}} = \begin{bmatrix} \frac{4}{5.07 + \epsilon} & \frac{5}{5.07 + \epsilon} & \frac{6}{5.07 + \epsilon} \end{bmatrix} \approx \begin{bmatrix} 0.789 & 0.986 & 1.183 \end{bmatrix} Normedrow2=[5.07+ϵ45.07+ϵ55.07+ϵ6]≈[0.7890.9861.183] - 应用可学习的缩放参数:
假设权重参数 weight \text{weight} weight 为一个向量 [ 1 , 1 , 1 ] [1, 1, 1] [1,1,1],表示每个元素的缩放因子。对于第 1 行: Output row1 = [ 0.462 ⋅ 1 0.925 ⋅ 1 1.387 ⋅ 1 ] = [ 0.462 0.925 1.387 ] \text{Output}_{\text{row1}} = \begin{bmatrix} 0.462 \cdot 1 & 0.925 \cdot 1 & 1.387 \cdot 1 \end{bmatrix} = \begin{bmatrix} 0.462 & 0.925 & 1.387 \end{bmatrix} Outputrow1=[0.462⋅10.925⋅11.387⋅1]=[0.4620.9251.387]对于第 2 行: Output row2 = [ 0.789 ⋅ 1 0.986 ⋅ 1 1.183 ⋅ 1 ] = [ 0.789 0.986 1.183 ] \text{Output}_{\text{row2}} = \begin{bmatrix} 0.789 \cdot 1 & 0.986 \cdot 1 & 1.183 \cdot 1 \end{bmatrix} = \begin{bmatrix} 0.789 & 0.986 & 1.183 \end{bmatrix} Outputrow2=[0.789⋅10.986⋅11.183⋅1]=[0.7890.9861.183]
实际代码实现
以下是使用 PyTorch 实现上述步骤的代码示例:
import torch
import torch.nn as nnclass RMSNorm(nn.Module):def __init__(self, dim: int, eps: float = 1e-6):super().__init__()self.eps = epsself.weight = nn.Parameter(torch.ones(dim))def _norm(self, x):return x * torch.rsqrt(x.pow(2).mean(-1, keepdim=True) + self.eps)def forward(self, x):output = self._norm(x.float()).type_as(x)return output * self.weight# 示例数据
data = torch.tensor([[1.0, 2.0, 3.0],[4.0, 5.0, 6.0]])# 实例化 RMSNorm 层
rms_norm = RMSNorm(dim=data.size(-1))# 计算归一化后的输出
normalized_data = rms_norm(data)print("Original Data:\n", data)
print("RMSNorm Normalized Data:\n", normalized_data)
结果
运行上述代码后,我们将得到归一化后的数据:
tensor([[1., 2., 3.],[4., 5., 6.]])
RMSNorm Normalized Data:tensor([[0.4629, 0.9258, 1.3887],[0.7895, 0.9869, 1.1843]], grad_fn=<MulBackward0>)
相关文章:

Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization)
Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization) flyfish 目录 Meta Llama 3 RMSNorm(Root Mean Square Layer Normalization)先看LayerNorm和BatchNorm举个例子计算 LayerNormRMSNorm 的整个计算过程实际代码实现结…...

MySQL-6、单表访问方法
前言 前面介绍了MySQL表空间相关的内容。包括区、段、碎片区,还有一些不同的页类型的作用。 (如果没有看前面五篇文章,不建议看此篇文章) 传送门: MySQL-1、InnoDB行格式 MySQL-2、InnoDB数据页 MySQL-3、索引 M…...

C语言实现三角波生成
C语言实现三角波生成 #include <stdio.h>#define SAMPLE_RATE 10000 // 采样率10kHz=10000Hz 对应100us=0.1ms #define UP_TIME 12.5 //上升时间12.5ms #...
WPF国际化的最佳实践
WPF国际化的最佳实践 1.创建项目资源文件 如果你的项目没有Properties文件夹和Resources.resx文件,可以通过右键项目-资源-常规-添加创建或打开程序集资源 2.添加国际化字符串 打开Resources.resx文件,添加需要翻译的文本字符,并将访问修…...
ctfshow web
【nl】难了 <?php show_source(__FILE__); error_reporting(0); if(strlen($_GET[1])<4){echo shell_exec($_GET[1]); } else{echo "hack!!!"; } ?> //by Firebasky //by Firebasky ?1>nl //先写个文件 ?1*>b //这样子会把所有文件名写在b里…...
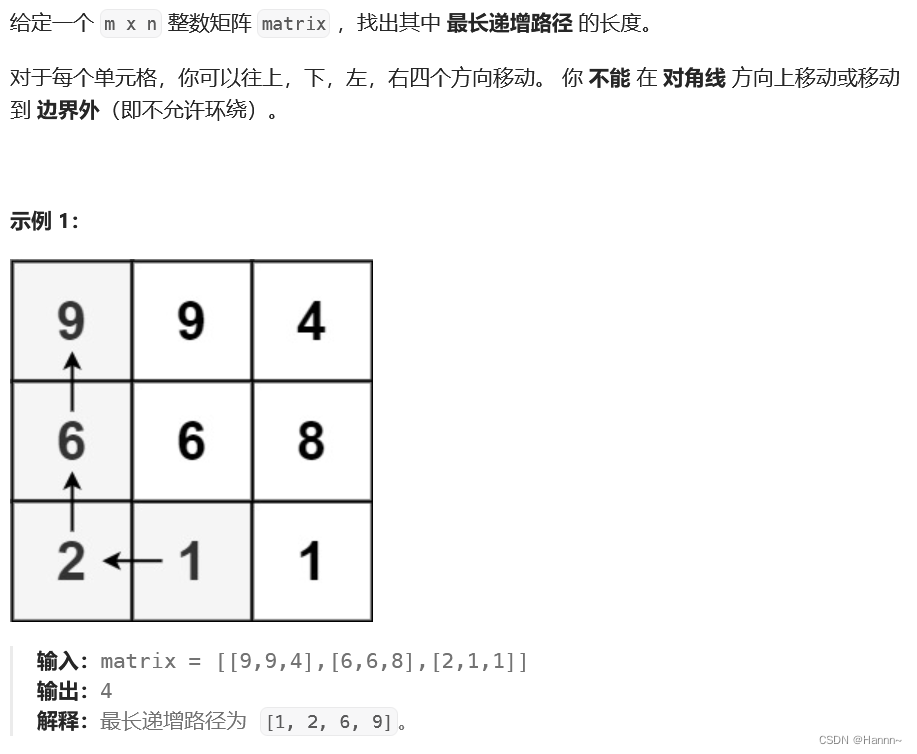
【力扣】矩阵中的最长递增路径
一、题目描述 二、解题思路 1、先求出以矩阵中的每个单元格为起点的最长递增路径 题目中说,对于每个单元格,你可以往上,下,左,右四个方向移动。那么以一个单元格为起点的最长递增路径就是:从该单元格往上…...
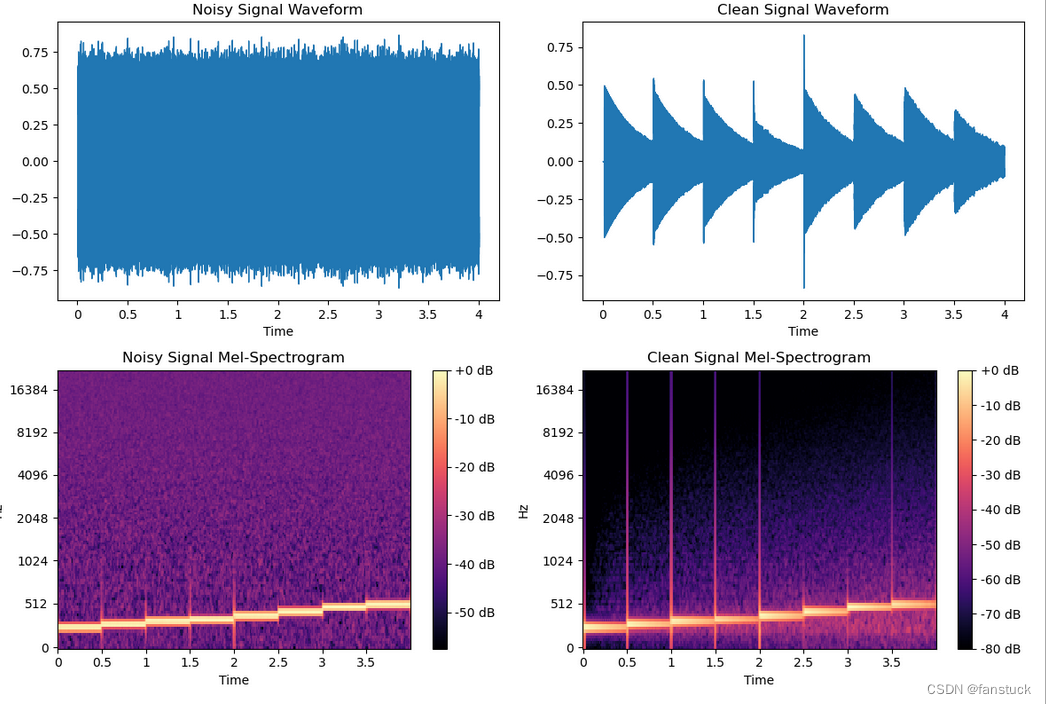
语音深度鉴伪识别项目实战:基于深度学习的语音深度鉴伪识别算法模型(二)音频数据预处理及去噪算法+Python源码应用
前言 深度学习技术在当今技术市场上面尚有余力和开发空间的,主流落地领域主要有:视觉,听觉,AIGC这三大板块。 目前视觉板块的框架和主流技术在我上一篇基于Yolov7-LPRNet的动态车牌目标识别算法模型已有较为详细的解说。与AIGC相…...

网络原理——http/https ---http(1)
T04BF 👋专栏: 算法|JAVA|MySQL|C语言 🫵 今天你敲代码了吗 网络原理 HTTP/HTTPS HTTP,全称为"超文本传输协议" HTTP 诞⽣与1991年. ⽬前已经发展为最主流使⽤的⼀种应⽤层协议. 实际上,HTTP最新已经发展到 3.0 但是当前行业中主要使用的HT…...
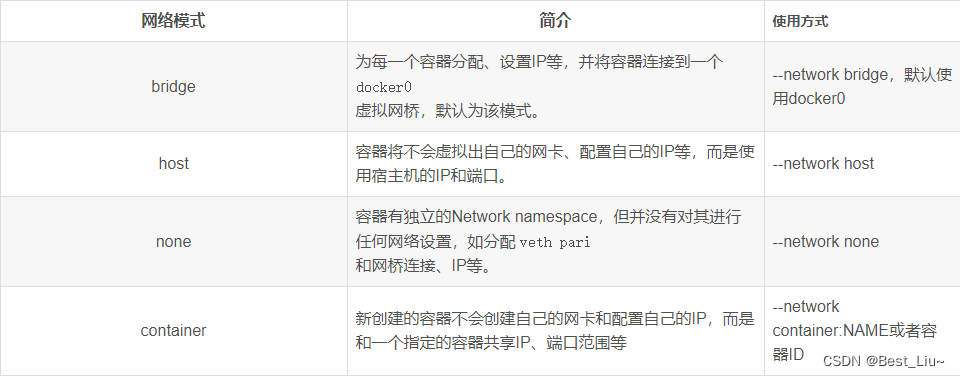
Docker安装、使用,容器化部署springboot项目
目录 一、使用官方安装脚本自动安装 二、Docker离线安装 1. 下载安装包 2. 解压 3.创建docker.service文件 4. 启动docker 三、docker常用命令 1. docker常用命令 2. docker镜像命令 3. docker镜像下载 4.docker镜像push到仓库 5. docker操作容器 6.docker …...
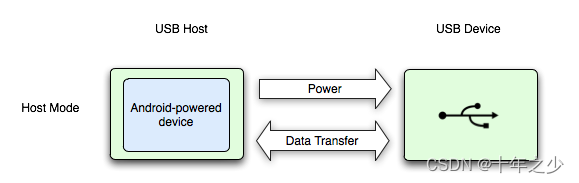
USB主机模式——Android
理论 摘自:USB 主机和配件概览 | Connectivity | Android Developers (google.cn) Android 通过 USB 配件和 USB 主机两种模式支持各种 USB 外围设备和 Android USB 配件(实现 Android 配件协议的硬件)。 在 USB 主机模式下࿰…...

240520Scala笔记
240520Scala笔记 第 7 章 集合 7.1 集合1 数组Array 集合(Test01_ImmutableArray): package chapter07 object Test01_ImmutableArray {def main(args: Array[String]): Unit {// 1. 创建数组val arr: Array[Int] new Array[Int](5)// 另一种创建方式val arr2 Array(…...
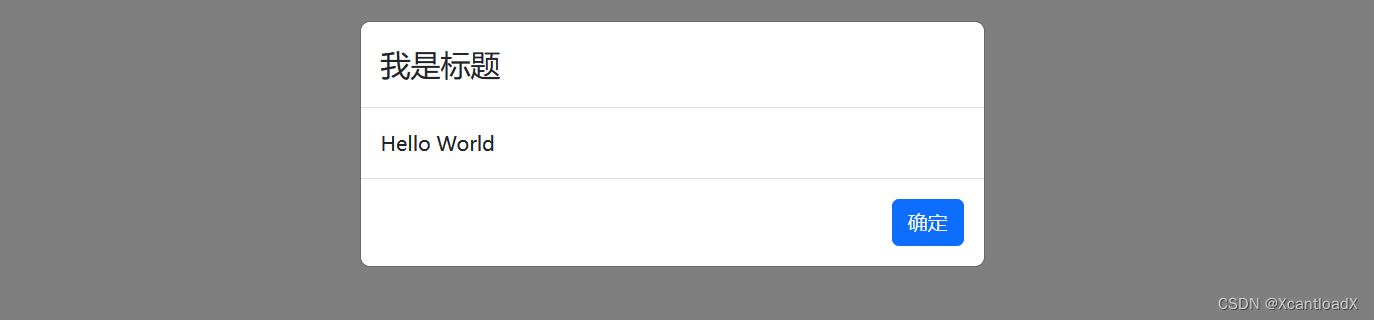
【React】封装一个好用方便的消息框(Hooks Bootstrap 实践)
引言 以 Bootstrap 为例,使用模态框编写一个简单的消息框: import { useState } from "react"; import { Modal } from "react-bootstrap"; import Button from "react-bootstrap/Button"; import bootstrap/dist/css/b…...
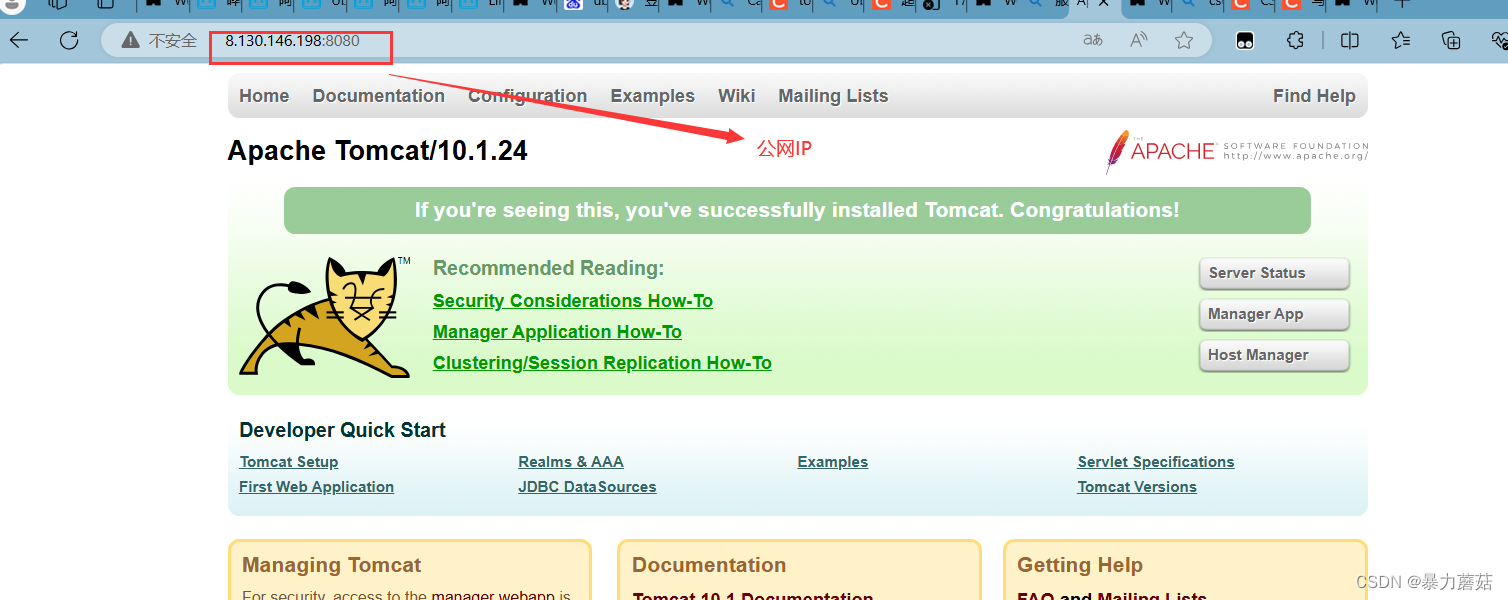
tomcat10部署踩坑记录-公网IP和服务器系统IP搞混
1. 服务器基本条件 使用的阿里云服务器,镜像系统是Ubuntu16.04java version “17.0.11” 2024-04-16 LTS装的是tomcat10.1.24阿里云服务器安全组放行了:8080端口 服务器防火墙关闭: 监听情况和下图一样: tomcat正常启动ÿ…...

探索Sass:Web开发的强大工具
在现代Web开发中,CSS(层叠样式表)作为前端样式设计的核心技术,已经发展得非常成熟。然而,随着Web应用的复杂性不断增加,传统的CSS书写方式逐渐暴露出一些不足之处,如代码冗长、难以维护、缺乏编程功能等。为了解决这些问题,Sass(Syntactically Awesome Stylesheets)应…...

vue组件之间的通信方式有哪些
在开发过程中,数据传输是一个核心的知识点,掌握了数据传输,相当于掌握了80%的内容。 Vue.js 提供了多种组件间的通信方式,这些方式适应不同的场景和需求。下面是4种常见的通信方式: 1. Props & Events (父子组件通…...
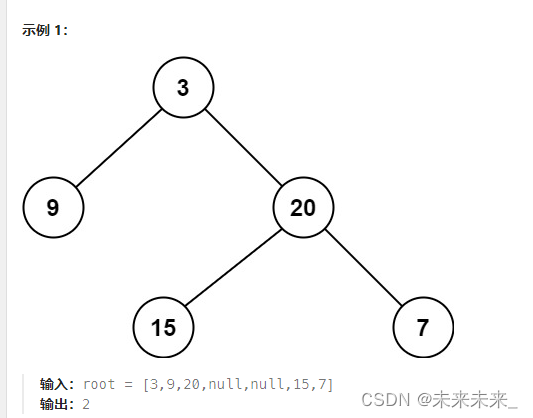
111、二叉树的最小深度
给定一个二叉树,找出其最小深度。最小深度是从根节点到最近叶子节点的最短路径上的节点数量。 题解:找出最小深度也就是找出根节点相对所有叶子结点的最小高度,在这也表明了根节点的高度是变化的,相对不同的叶子结点有不同的高度。…...
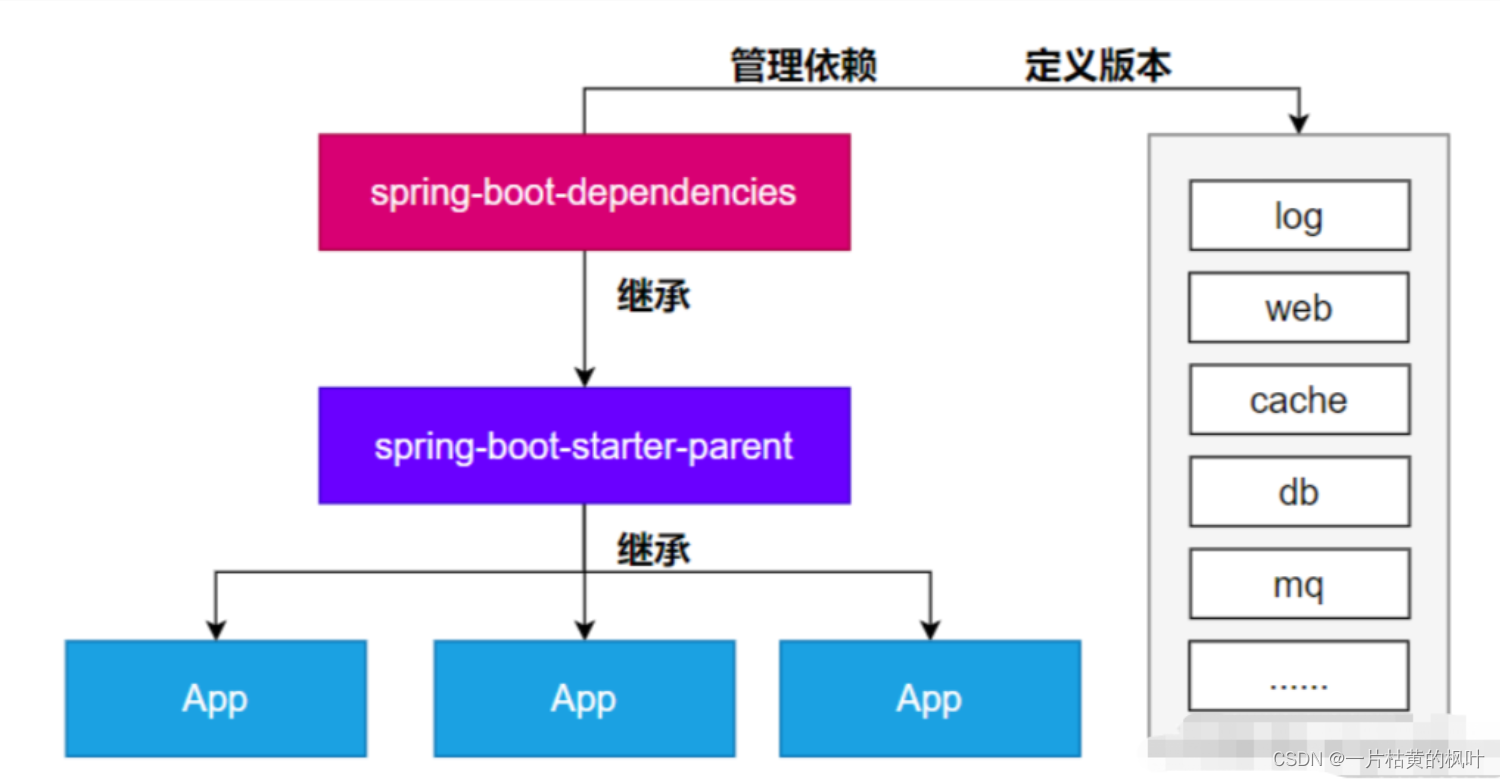
SpringBoot3依赖管理,自动配置
文章目录 1. 项目新建2. 相关pom依赖3. 依赖管理机制导入 starter 所有相关依赖都会导入进来为什么版本号都不用写?如何自定义版本号第三方的jar包 4. 自动配置机制5. 核心注解 1. 项目新建 直接建Maven项目通过官方提供的Spring Initializr项目创建 2. 相关pom依…...

音视频开发17 FFmpeg 音频解码- 将 aac 解码成 pcm
这一节,接 音视频开发12 FFmpeg 解复用详情分析,前面我们已经对一个 MP4文件,或者 FLV文件,或者TS文件进行了 解复用,解出来的 视频是H264,音频是AAC,那么接下来就要对H264和AAC进行处理,这一节…...
)
vue2中封装图片上传获取方法类(针对后端返回的数据不是图片链接,只是图片编号)
在Vue 2中实现商品列表中带有图片编号,并将返回的图片插入到商品列表中,可以通过以下步骤完成: 在Vue组件的data函数中定义商品列表和图片URL数组。 创建一个方法来获取每个商品的图片URL。 使用v-for指令在模板中遍历商品列表,并…...
this指针和静态成员)
【C++面向对象编程】(二)this指针和静态成员
文章目录 this指针和静态成员this指针静态成员 this指针和静态成员 this指针 C中类的成员变量和成员函数的存储方式有所不同: 成员变量:对象的成员变量直接作为对象的一部分存储在内存中。成员函数:成员函数(非静态成员函数&am…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

谷歌浏览器插件
项目中有时候会用到插件 sync-cookie-extension1.0.0:开发环境同步测试 cookie 至 localhost,便于本地请求服务携带 cookie 参考地址:https://juejin.cn/post/7139354571712757767 里面有源码下载下来,加在到扩展即可使用FeHelp…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...
