算法——二分查找
介绍
二分查找是一个高效的查找算法,查找算法还有线性查找,它的时间复杂度为 O ( n ) O(n) O(n),但二分查找的时间复杂度为 l o g ( n ) log(n) log(n)(因为是2分,所以此处的log是以2为底的对数函数)。
注:本文提到的查找都是无重复元素的,要是有重复元素,就比较麻烦了。
线性查找
思想
从数组的头部向尾部遍历,如果找到就返回它的下标,如果遍历完还找不到就返回-1。
代码
class Solution {public int linearSearch(int[] nums, int target) {for (int i = 0; i < nums.length; i++) {if (nums[i] == target) {return i;}}return -1;}
}
二分查找
前提
数组是有序的,一般要求数组为升序排列,也就是从小到大排列。
思想
二分查找的核心思想就是分治,分就是将一个问题划分为多个子问题,治就是将最小的子问题解决。比如说有一堆苹果,要想吃完这堆苹果(解决一个大问题),就得先将这堆苹果分成很多堆(将问题划分为子问题),直到每堆只剩一个苹果(划分到了最小的子问题),然后再一个一个地将苹果吃掉(将最小的子问题解决)。
现在理解二分查找,二分查找就是找到升序的数组的中间元素,然后比较中间元素与目标元素的大小,如果目标元素等于中间元素,则直接返回中间元素的下标;如果目标元素大于中间元素,就去右子区间查找;否则就去左子区间查找。直到找到目标元素或无法再找为止(无法再找指的是区间的长度小于1)。注意,如果数组是降序的,则策略与此恰好相反。
由于二分查找每次都将待查找区间缩小为上一个待查找区间的一半,所以它的时间复杂度为 O ( l o g n ) O(logn) O(logn)。
代码
class Solution {public int binarySearch(int[] nums, int target) {// nums一定要有序,如果没有序,就先使用Arrays.sort(nums);将nums按升序排列int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + (right - left >> 1);if (nums[mid] == target) {return mid;} else if (nums[mid] < target) {left = mid + 1;} else {right = mid - 1;}}return -1;}
}
相关文章:

算法——二分查找
介绍 二分查找是一个高效的查找算法,查找算法还有线性查找,它的时间复杂度为 O ( n ) O(n) O(n),但二分查找的时间复杂度为 l o g ( n ) log(n) log(n)(因为是2分,所以此处的log是以2为底的对数函数)。 注…...
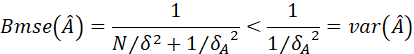
统计信号处理基础 习题解答10-8
题目 一个随机变量具有PDF 。希望在没有任何可用数据的情况下估计的一个现实。为此提出了使最小的MMSE估计量,其中期望仅是对求的。证明MMSE估计量为。将你的结果应用到例10.1,当把数据考虑进去时,证明最小贝叶斯MSE是减少的。 解答 在贝叶…...

Flutter打包网络问题解决办法
问题情况":app:compileReleaseJavaWithJavac" 报错的最主要问题其实在下一句 Failed to find Build Tools revision 30.0.3,请查看自己的Android sdk版本,比如我的就是’34.0.0’版本. 解决办法: 在app/build.gradle中的android下添加,即可 buildToolsVersion 3…...

【ARM Cache 及 MMU 系列文章 6.3 -- ARMv8/v9 Cache Tag数据读取及分析】
请阅读【ARM Cache 及 MMU/MPU 系列文章专栏导读】 及【嵌入式开发学习必备专栏】 文章目录 Cache Tag 数据读取测试代码Cache Tag 数据读取 在处理器中,缓存是一种快速存储资源,用于减少访问主内存时的延迟。缓存通过存储主内存中经常访问的数据来实现这一点。为了有效地管…...

Lua移植到标准ANSI C环境
本文目录 1、引言2、环境准备2.1 源码下载2.2 项目构建环境准备 3、项目编译3.1 添加main.c3.2 Kconfig选择模块3.3 项目构建3.4 项目编译 4、运行 文章对应视频教程: 在下方喔 ~~~ 欢迎关注 点击图片或链接访问我的B站主页~~~ lau解释器移植与功能验证 1、引言 本…...

crossover软件安装程序怎么安装 Crossover for Mac切换Windows系统 crossover软件怎么样
CrossOver Mac版是专为苹果电脑用户打造的一款实用工具,这款工具主要方便用户在Mac上运行windows系列的应用程序,用户不需要安装虚拟机就可以实现各种应用程序的直接应用,并且可以实现无缝集成,实现跨平台的复制粘贴和文件互通等&…...

【2024高考作文】新课标I卷-人工智能主题,用chatGPT作答
目录 🐸🐸作文真题 ⭐⭐1.chatGPT作答 ⭐⭐2.通义千问作答 ⭐⭐3.KiMi作答 整理不易,欢迎一键三连!!! 送你们一条美丽的--分割线-- 🐸🐸作文真题 随着互联网的普及、人工智能的…...

【计算机网络】P2 计算机网络体系结构基本概念,涉及分层的基本术语、SDU、PCI 与 PDU 的概念以及层次结构的含义
目录 概述分层的基本元组基本术语SDU、PCI 以及 PDU层次结构含义 概述 在两个系统中实体间的通信是一个很复杂的过程。而为了降低协议设计以及调试过程的复杂性,同时便于对网络进行研究、实现和维护,促进标准化工作,通常对计算机网络的体系结…...
)
主流物联网协议客户端开源库介绍(mqtt,coap,websocket,httphttps,tcp及udp)
一.概述 本文主要介绍主流物联网协议(mqtt,coap,websocket,http/https,tcp/udp)客户端c/c开源库,并对其特点进行对比分析。 二.各个库具体介绍 1.MQTT (1)常见的c/c客户…...

【Python】成功解决SyntaxError: invalid syntax
【Python】成功解决SyntaxError: invalid syntax 下滑即可查看博客内容 🌈 欢迎莅临我的个人主页 👈这里是我静心耕耘深度学习领域、真诚分享知识与智慧的小天地!🎇 🎓 博主简介:985高校的普通本硕&am…...

源代码防泄密
深信达SDC沙盒数据防泄密系统,是专门针对敏感 数据防泄密的保护系统,尤其是对研发型企业数据 防泄密保护。实现对数据的代码级保护,且不影响 工作效率,不影响正常使用。所有敏感数据都自动 加密并配合多种管控机制,从而…...
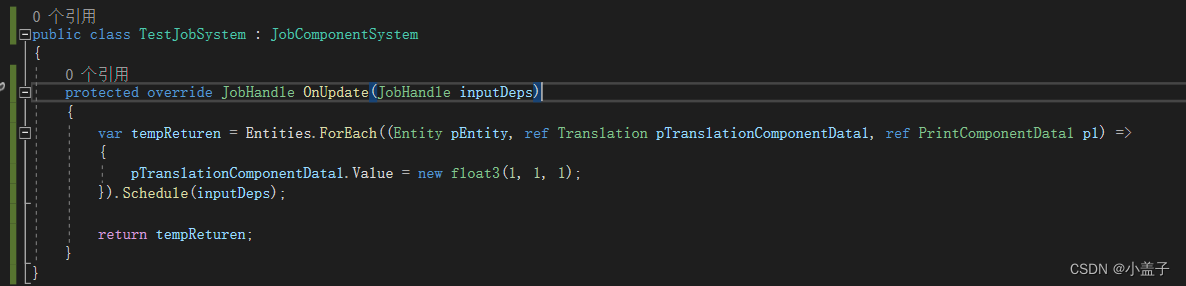
Unity DOTS技术(十三) ComponentSystem及JobComponentSystem
文章目录 一.ComponentSystem介绍二.JobComponentSystem 一.ComponentSystem介绍 1.继承ComponentSystem需要实现抽象OnUpdate() 2.与SystemBase不同,ComponentSystem不包含LambdaSingleJobDescription, 3.CompoentSystem的带代码都是在主线程上运行,不支持多线程. 4.并不能在…...
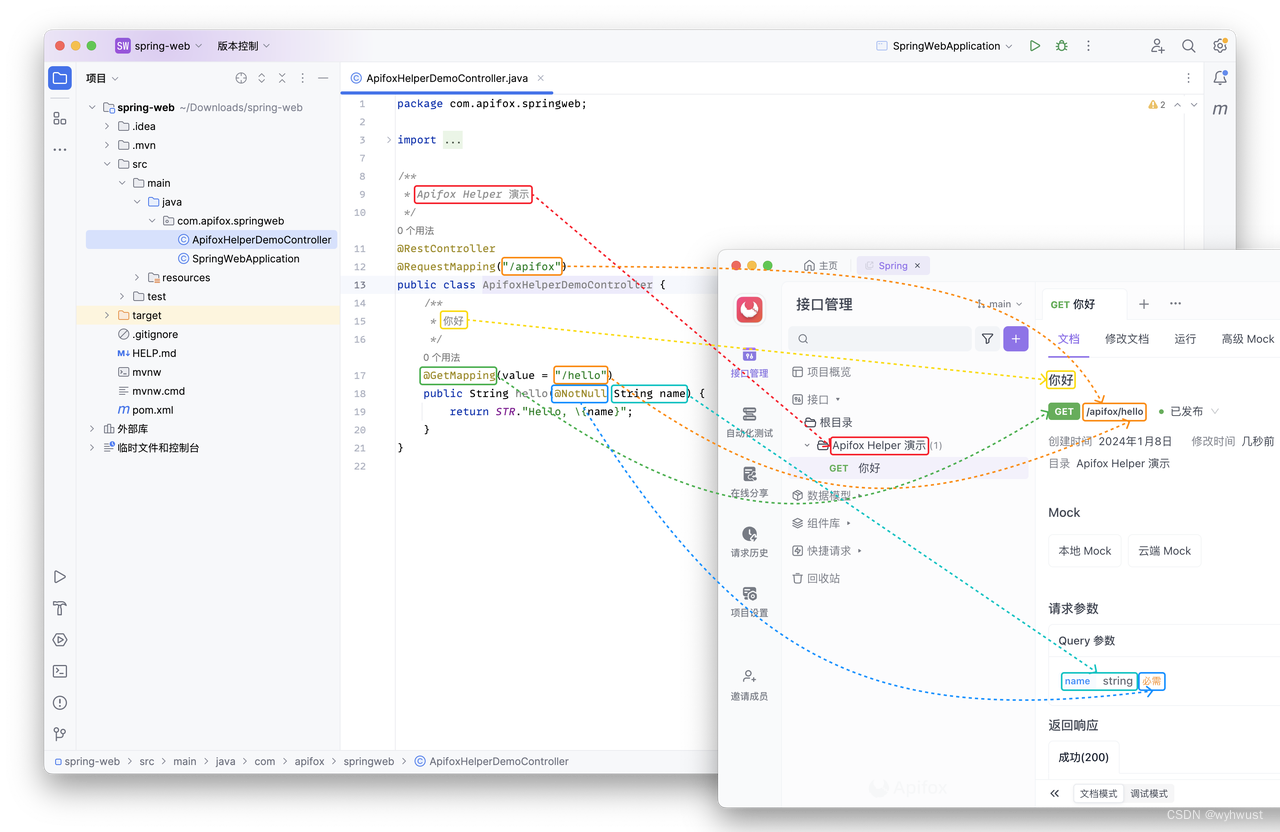
Apifox的使用
1、了解Apifox的工具特点和使用方法 2、使用Apifox辅助生成接口文档,尝试使用Apifox进行其他前后端调试。 Apifox IDEA 插件快速上手 | Apifox 帮助文档 Apifox IDEA 插件来啦!是真的超好用!_哔哩哔哩_bilibili 21分钟学会Apifox_哔哩哔哩…...

【SpringBoot】SpringBoot整合RabbitMQ消息中间件,实现延迟队列和死信队列
📝个人主页:哈__ 期待您的关注 目录 一、🔥死信队列 RabbitMQ的工作模式 死信队列的工作模式 二、🍉RabbitMQ相关的安装 三、🍎SpringBoot引入RabbitMQ 1.引入依赖 2.创建队列和交换器 2.1 变量声明 2.2 创建…...

kafka消息积压处理方案
背景: 某值班的一天,生产出现消息积压问题,对此类的问题做出快速应对方案来避免同类型问题,防止影响范围进一步的扩大。 出现消费积压后如何处理: 首先优先处理消息积压,如果代码逻辑问题,立…...

【vscode-快捷键 一键JSON格式化】
网上有很多JSON格式化工具,也有很多好用的在线json格式化工具。但是其实Vscode里面的可以直接格式化JSON,这里分享一个我常用的小插件 Prettify JSON 未格式化的JSON数据 召唤出命令行,输入prettify JSON 即可! ✿✿ヽ(▽)ノ✿...

什么是 Spring Boot 的起步依赖和自动配置?它们的作用是什么?
Spring Boot 的起步依赖和自动配置是 Spring Boot 框架的两个核心特性,它们的作用主要是简化了 Spring Boot 项目的搭建和配置过程。 起步依赖(Starter Dependencies):起步依赖是一种预先定义好的依赖关系集合,它包含…...
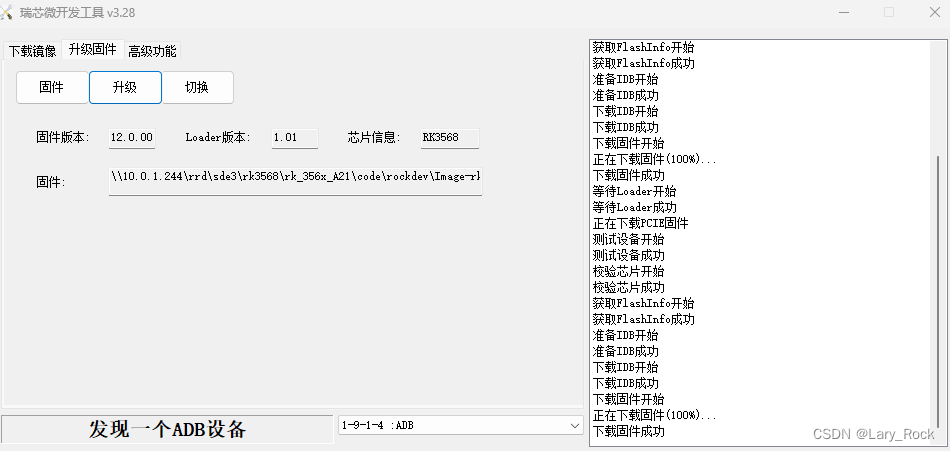
rk3568 norflash+pcei nvme 配置
文章目录 rk3568 norflashpcei nvme 配置1,添加parameter_nor.txt文件2 修改编译规则3 修改uboot4 修改BoardConfig.mk5 修改kernel pcei配置6 编译7 烧录 rk3568 norflashpcei nvme 配置 1,添加parameter_nor.txt文件 device/rockchip/rk356x/rk3568_…...

【Vue】面经基础版-首页请求渲染
步骤分析 1.安装axios 2.看接口文档,确认请求方式,请求地址,请求参数 3.created中发送请求,获取数据,存储到data中 4.页面动态渲染 代码实现 1.安装axios yarn add axios npm i axios 2.接口文档 请求地址: …...
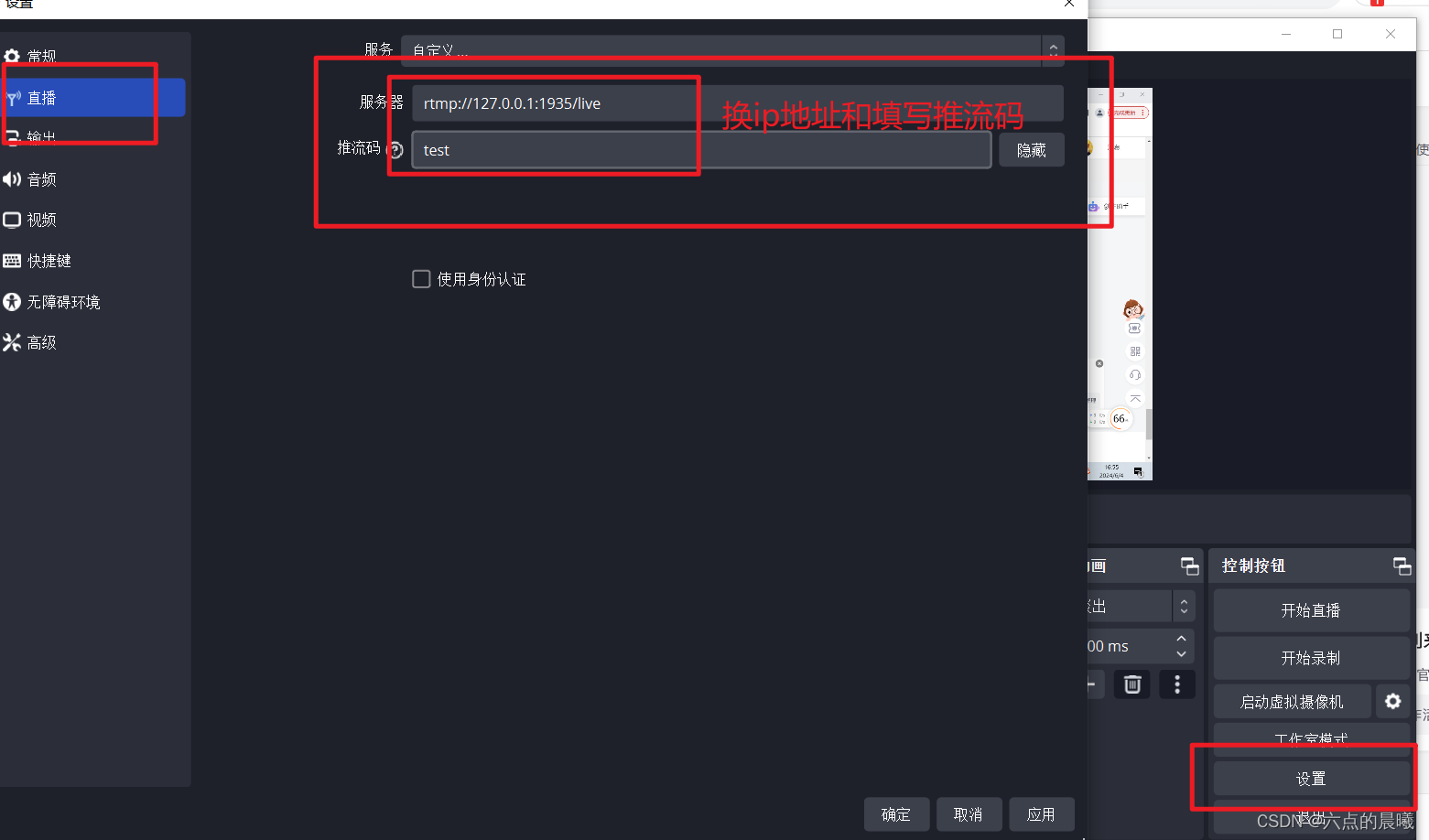
OBS+nginx+nginx-http-flv-module实现阿里云的推流和拉流
背景:需要将球机视频推送到阿里云nginx,使用网页和移动端进行播放,以前视频格式为RTMP,但是在网页上面播放RTMP格式需要安装flash插件,chrome浏览器不给安装,调研后发现可以使用nginx的模块nginx-http-flv-…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
Mybatis逆向工程,动态创建实体类、条件扩展类、Mapper接口、Mapper.xml映射文件
今天呢,博主的学习进度也是步入了Java Mybatis 框架,目前正在逐步杨帆旗航。 那么接下来就给大家出一期有关 Mybatis 逆向工程的教学,希望能对大家有所帮助,也特别欢迎大家指点不足之处,小生很乐意接受正确的建议&…...

oracle与MySQL数据库之间数据同步的技术要点
Oracle与MySQL数据库之间的数据同步是一个涉及多个技术要点的复杂任务。由于Oracle和MySQL的架构差异,它们的数据同步要求既要保持数据的准确性和一致性,又要处理好性能问题。以下是一些主要的技术要点: 数据结构差异 数据类型差异ÿ…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

从零实现STL哈希容器:unordered_map/unordered_set封装详解
本篇文章是对C学习的STL哈希容器自主实现部分的学习分享 希望也能为你带来些帮助~ 那咱们废话不多说,直接开始吧! 一、源码结构分析 1. SGISTL30实现剖析 // hash_set核心结构 template <class Value, class HashFcn, ...> class hash_set {ty…...

多模态大语言模型arxiv论文略读(108)
CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文标题:CROME: Cross-Modal Adapters for Efficient Multimodal LLM ➡️ 论文作者:Sayna Ebrahimi, Sercan O. Arik, Tejas Nama, Tomas Pfister ➡️ 研究机构: Google Cloud AI Re…...

基于SpringBoot在线拍卖系统的设计和实现
摘 要 随着社会的发展,社会的各行各业都在利用信息化时代的优势。计算机的优势和普及使得各种信息系统的开发成为必需。 在线拍卖系统,主要的模块包括管理员;首页、个人中心、用户管理、商品类型管理、拍卖商品管理、历史竞拍管理、竞拍订单…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

uni-app学习笔记三十五--扩展组件的安装和使用
由于内置组件不能满足日常开发需要,uniapp官方也提供了众多的扩展组件供我们使用。由于不是内置组件,需要安装才能使用。 一、安装扩展插件 安装方法: 1.访问uniapp官方文档组件部分:组件使用的入门教程 | uni-app官网 点击左侧…...
