Day51 动态规划part10+Day52 动态规划part11
LC121买卖股票的最佳时机(未掌握)
- 暴力:双层循环寻找最优间距,每一次都确定一个起点,遍历剩余节点当作终点
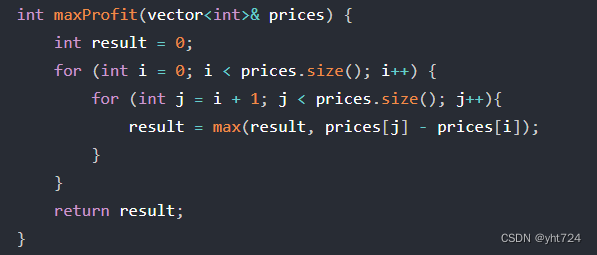
- 贪心:取最左最小值,不断遍历那么得到的差值最最大值就是最大利润。
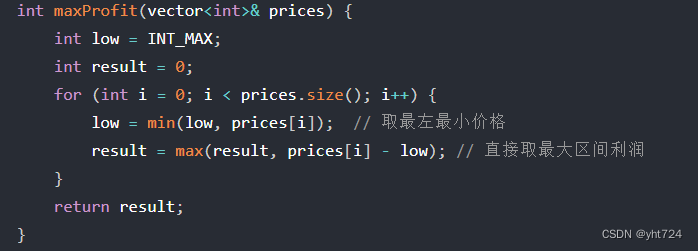
- 动态规划
- dp数组的含义:
- dp[i][0] 表示第i天持有股票所得最多现金
- dp[i][1] 表示第i天不持有股票所得最多现金
- 递归式的推导
- dp[i][0]=>第i-1天持有和第i天买入的最多现金=>Math.max(dp[i-1][0],-price[i])
- 因为本金是0,且只能操作一次,所以第i天买入的最多现金为-price[i]
- dp[i][1]=>第i-1天不持有和第i天卖出的最多现金=>Math.max(dp[i-1][1],dp[i-1][0]+price[i])
- dp数组的含义:
- 代码

LC122买卖股票的最佳时机II
- 与LC121买卖股票的最佳时机不同的是,LC121只能买入卖出一次,而LC122可以买入卖出多次,因此第i天买入的最多现金为dp[i-1][1]-price[i]
- 代码
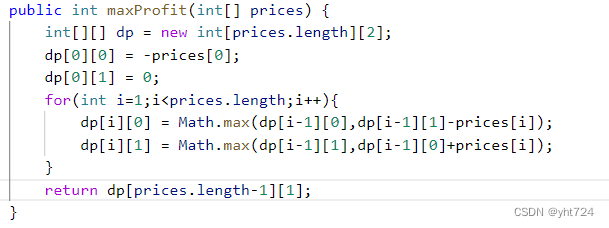
LC123买卖股票的最佳时机III(未掌握)
- LC123与LC122不同的是,LC123只能允许买入两次,而LC122可以买入无数次,因此使用5个状态来记录五种情况
- 0:无操作,这个状态是用来帮助统计第一次持有股票的情况的
- 1:第一次持有股票
- 2:第一次不持有股票
- 3:第二次持有股票
- 4:第二次不持有股票
- 递归公式
- dp[i][0] = dp[i-1][0]
- dp[i][1] => 第i-1天第一次就持有股票和第i-1天不持有股票第i天买入 => Math.max(dp[i-1][1], dp[i-1][0]-price[i])
- dp[i][2] => 第i-1天第一次就不持有股票和第i-1天持有股票第i天卖出 => Math.max(dp[i-1][2], dp[i-1][1]+price[i])
- dp[i][3] => 第i-1天第二次就持有股票和第i-1天第一次不持有股票第i天买入第二次 => Math.max(dp[i-1][3], dp[i-1][2]+price[i])
- dp[i][4] => 第i-1天第二次就不持有股票和第i-1天持有第二次股票第i天卖出 => Math.max(dp[i-1][4], dp[i-1][3]+price[i])
- 初始化:
- 第0天没有操作,这个最容易想到,就是0,即:dp[0][0] = 0;
- 第0天做第一次买入的操作,dp[0][1] = -prices[0];
- 第0天做第一次卖出的操作,可以理解为当天买入,当天卖出,所以dp[0][2] = 0;
- 第0天第二次买入操作,可以理解为第二次买入依赖于第一次卖出的状态,其实相当于第0天第一次买入了,第一次卖出了,然后再买入一次(第二次买入),初始化为:dp[0][3] = -prices[0];
- 同理第二次卖出初始化dp[0][4] = 0;
- 代码

LC188买卖股票的最佳时机IV
- LC123是买入两次,LC188是买入k次,因此j的值应该设置为2k+1种,代表2k+1种情况
- 根据规律可知
- 初始化的时候dp[0][j],只要j为1、3、5…2*k-1时,值为-price[0]
- 同理:j两两一组,表示j次买入股票和卖出股票的最多金额
- 代码

相关文章:

Day51 动态规划part10+Day52 动态规划part11
LC121买卖股票的最佳时机(未掌握) 暴力:双层循环寻找最优间距,每一次都确定一个起点,遍历剩余节点当作终点 贪心:取最左最小值,不断遍历那么得到的差值最最大值就是最大利润。 动态规划 dp数组…...
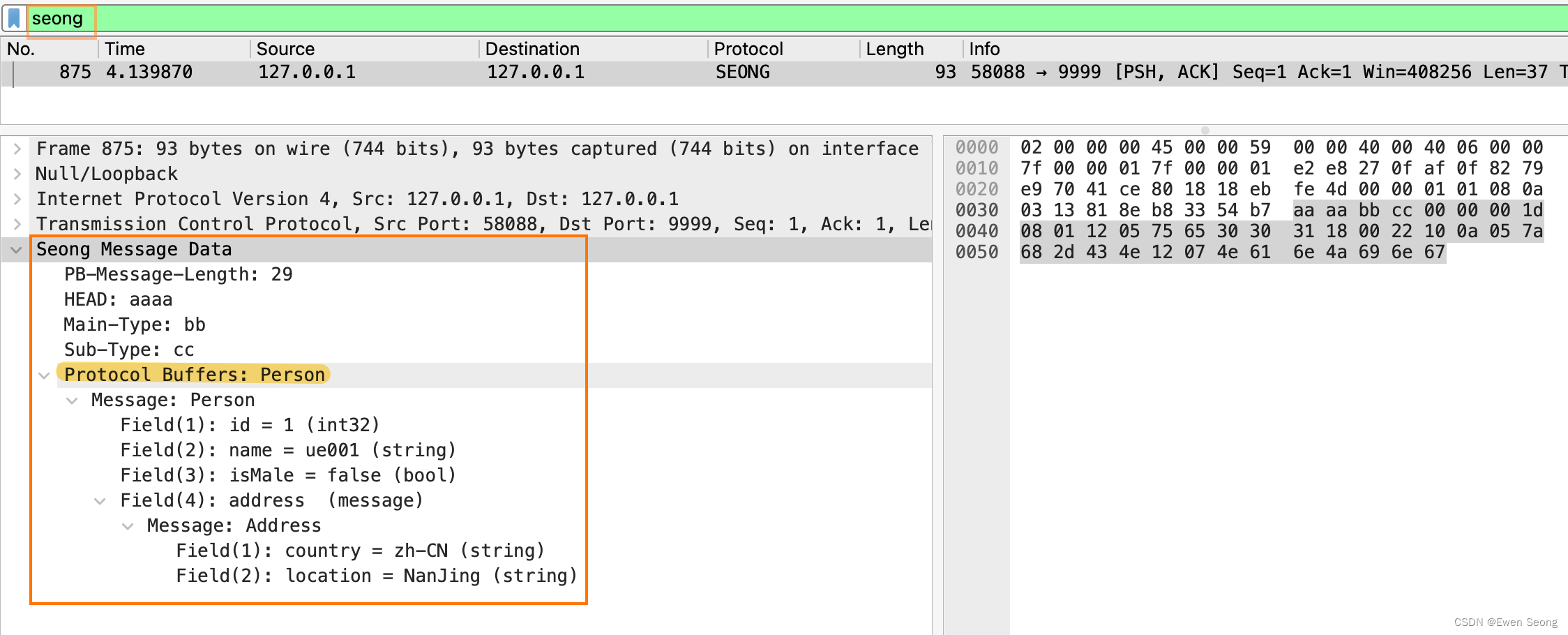
Wireshark自定义Lua插件
背景: 常见的抓包工具有tcpdump和wireshark,二者可基于网卡进行抓包:tcpdump用于Linux环境抓包,而wireshark用于windows环境。抓包后需借助包分析工具对数据进行解析,将不可读的二进制数转换为可读的数据结构。 wires…...

商城项目【尚品汇】07分布式锁-2 Redisson篇
文章目录 1 Redisson功能介绍2 Redisson在Springboot中快速入门(代码)2.1 导入依赖2.2 Redisson配置2.3 将自定义锁setnx换成Redisson实现(可重入锁) 3 可重入锁原理3.1 自定义分布式锁setnx为什么不可以重入3.2 redisson为什么可…...

Adobe Illustrator 矢量图设计软件下载安装,Illustrator 轻松创建各种矢量图形
Adobe Illustrator,它不仅仅是一个简单的图形编辑工具,更是一个拥有丰富功能和强大性能的设计利器。 在这款软件中,用户可以通过各种精心设计的工具,轻松创建和编辑基于矢量路径的图形文件。这些矢量图形不仅具有高度的可编辑性&a…...

Nvidia/算能 +FPGA+AI大算力边缘计算盒子:中国舰船研究院
中国舰船研究院又称中国船舶重工集团公司第七研究院,隶属于中国船舶重工集团公司,是专门从事舰船研究、设计、开发的科学技术研究机构,是中国船舶重工集团公司的军品技术研究中心、科技开发中心;主要从事舰船武器装备发展战略研究…...
双网卡配置IP和路由总结
1.在网络适配器属性IPv4中设置默认网关(记网关地址为A),将会在本地路由表中新增一条记录: 网络号子网掩码网关地址0.0.0.00.0.0.0A 2.如果有两个网卡(假设一个连接内网,一个连接互联网)&#…...

【纯血鸿蒙】——自适应布局如何实现?
界面级一多能力有 2 类: 自适应布局: 略微调整界面结构 响应式布局:比较大的界面调整 本文章先主要讲解自适应布局,响应式布局再后面文章再细讲。话不多说,开始了。 自适应布局 针对常见的开发场景,方舟开发框架提…...

Qt5学习笔记(一):Qt Widgets Application项目初探
笔者长期使用MFC开发Windows GUI软件。随着软件向Linux平台迁移的趋势越发明朗,GUI程序的跨平台需求也越来越多。因此笔者计划重新抓一下Qt来实现跨平台GUI程序的实现。 0x01. 看看Qt Widgets Application项目结构 打开Qt5,点击“ New”按钮新建项目。…...

Linux网络编程:数据链路层协议
目录 前言: 1.以太网 1.1.以太网帧格式 1.2.MTU(最大传输单元) 1.2.1.IP协议和MTU 1.2.2.UDP协议和MTU 1.2.3.TCP协议和MTU 2.ARP协议(地址解析协议) 2.1.ARP在局域网通信的角色 2.2.ARP报文格式 2.3.ARP报文…...

企业估值的三种方法
估值模型三剑客—DCF、P/E、EV /EBITDA 三种主要估值模型的优缺点: DCF 优点:通过对自由现金流的折现计算,反映了公司内在价值的本质,是最重要与最合理的估值方法。 缺点:未来自由现金流的估计不准确,受折现率影响…...

比亚迪正式签约国际皮划艇联合会和中国皮划艇协会,助推龙舟入奥新阶段
6月5日,比亚迪与国际皮划艇联合会、中国皮划艇协会在深圳共同签署合作协议,国际皮划艇联合会主席托马斯科涅茨科,国际皮划艇联合会秘书长理查德派蒂特,中国皮划艇协会秘书长张茵,比亚迪品牌及公关处总经理李云飞&#…...

宏集Panorama SCADA:个性化定制,满足多元角色需求
前言 在考虑不同人员在企业中的职能和职责时,他们对于SCADA系统的需求可能因其角色和工作职责的不同而有所差异。在SCADA系统的设计和实施过程中,必须充分考虑和解决这种差异性。 为了满足不同人员的需求, 宏集Panorama SCADA平台具备灵活的功能和定制…...

聪明人社交的基本顺序:千万别搞反了,越早明白越好
聪明人社交的基本顺序:千万别搞反了,越早明白越好 国学文化 德鲁克博雅管理 2024-03-27 17:00 作者:方小格 来源:国学文化(gxwh001) 导语 比一个好的圈子更重要的,是自己优质的能力。 唐诗宋…...
图片和PDF展示预览、并支持下载
需求 展示图片和PDF类型,并且点击图片或者PDF可以预览 第一步:遍历所有的图片和PDF列表 <div v-for"(data,index) in parerFont(item.fileInfo)" :key"index" class"data-list-item"><downloadCard :file-inf…...

图论第5天
127.单词接龙 需要cout看一下过程。 #include <iostream> #include <queue> #include <stack> #include <unordered_map> #include <unordered_set> #include <vector> using namespace ::std;class Solution { public:int ladderLength(…...

Java开发-面试题-0004-HashMap 和 Hashtable的区别
Java开发-面试题-0004-HashMap 和 Hashtable的区别 更多内容欢迎关注我(持续更新中,欢迎Star✨) Github:CodeZeng1998/Java-Developer-Work-Note 技术公众号:CodeZeng1998(纯纯技术文) 生活…...

Swift 序列(Sequence)排序面面俱到 - 从过去到现在(一)
概览 在任何语言中对序列(或集合)元素的排序无疑是一种司空见惯的常规操作,在 Swift 语言里自然也不例外。序列排序看似简单,实则“暗藏玄机”。 要想真正掌握 Swift 语言中对排序的“各种姿势”,我们还得从长计议。不如就先从最简单的排序基本功开始聊起吧。 在本篇博…...

redis 04 redis结构
1.客户端...
【原创】springboot+mysql农业园区管理系统设计与实现
个人主页:程序猿小小杨 个人简介:从事开发多年,Java、Php、Python、前端开发均有涉猎 博客内容:Java项目实战、项目演示、技术分享 文末有作者名片,希望和大家一起共同进步,你只管努力,剩下的交…...

web前端 孙俏:深度探索与实战之路
web前端 孙俏:深度探索与实战之路 在这个数字化、信息化的时代,web前端技术以其独特的魅力,吸引着越来越多的开发者投身其中。今天,我们将跟随孙俏的脚步,一同探索web前端的深度与广度,揭开其神秘的面纱。…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

2023赣州旅游投资集团
单选题 1.“不登高山,不知天之高也;不临深溪,不知地之厚也。”这句话说明_____。 A、人的意识具有创造性 B、人的认识是独立于实践之外的 C、实践在认识过程中具有决定作用 D、人的一切知识都是从直接经验中获得的 参考答案: C 本题解…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

Caliper 配置文件解析:fisco-bcos.json
config.yaml 文件 config.yaml 是 Caliper 的主配置文件,通常包含以下内容: test:name: fisco-bcos-test # 测试名称description: Performance test of FISCO-BCOS # 测试描述workers:type: local # 工作进程类型number: 5 # 工作进程数量monitor:type: - docker- pro…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
