B3870 [GESP202309 四级] 变长编码
[GESP202309 四级] 变长编码
题目描述
小明刚刚学习了三种整数编码方式:原码、反码、补码,并了解到计算机存储整数通常使用补码。但他总是觉得,生活中很少用到 2 31 − 1 2^{31}-1 231−1 这么大的数,生活中常用的 0 ∼ 100 0\sim 100 0∼100 这种数也同样需要用 4 4 4 个字节的补码表示,太浪费了些。
热爱学习的小明通过搜索,发现了一种正整数的变长编码方式。这种编码方式的规则如下:
1 . 对于给定的正整数,首先将其表达为二进制形式。例如, ( 0 ) { 10 } = ( 0 ) { 2 } (0)_{\{10\}}=(0)_{\{2\}} (0){10}=(0){2}, ( 926 ) { 10 } = ( 1110011110 ) { 2 } (926)_{\{10\}}=(1110011110)_{\{2\}} (926){10}=(1110011110){2}。
2 . 将二进制数从低位到高位切分成每组 7 7 7 bit,不足 7 7 7bit 的在高位用 0 0 0 填补。例如, ( 0 ) { 2 } (0)_{\{2\}} (0){2} 变为 0000000 0000000 0000000 的一组, ( 1110011110 ) { 2 } (1110011110)_{\{2\}} (1110011110){2} 变为 0011110 0011110 0011110 和 0000111 0000111 0000111 的两组。
3 . 由代表低位的组开始,为其加入最高位。如果这组是最后一组,则在最高位填上 0 0 0,否则在最高位填上 1 1 1。于是, 0 0 0 的变长编码为 00000000 00000000 00000000 一个字节, 926 926 926 的变长编码为 10011110 10011110 10011110 和 00000111 00000111 00000111 两个字节。
这种编码方式可以用更少的字节表达比较小的数,也可以用很多的字节表达非常大的数。例如, 987654321012345678 987654321012345678 987654321012345678 的二进制为 ( 0001101 1011010 0110110 1001011 1110100 0100110 1001000 0010110 1001110 ) { 2 } (0001101 \ 1011010 \ 0110110 \ 1001011 \ 1110100 \ 0100110 \ 1001000 \ 0010110 \ 1001110)_{\{2\}} (0001101 1011010 0110110 1001011 1110100 0100110 1001000 0010110 1001110){2},于是它的变长编码为(十六进制表示) CE 96 C8 A6 F4 CB B6 DA 0D,共 9 9 9 个字节。
你能通过编写程序,找到一个正整数的变长编码吗?
输入格式
输入第一行,包含一个正整数 N N N。约定 0 ≤ N ≤ 1 0 18 0\le N \le 10^{18} 0≤N≤1018。
输出格式
输出一行,输出 N N N 对应的变长编码的每个字节,每个字节均以 2 2 2 位十六进制表示(其中, A-F 使用大写字母表示),两个字节间以空格分隔。
样例 #1
样例输入 #1
0
样例输出 #1
00
样例 #2
样例输入 #2
926
样例输出 #2
9E 07
样例 #3
样例输入 #3
987654321012345678
样例输出 #3
CE 96 C8 A6 F4 CB B6 DA 0D
题目解析
题目描述:
给定一个非负整数N,将其按照变长编码的规则进行编码。变长编码的规则如下:
- 对于给定的正整数,首先将其表达为二进制形式。
- 将二进制数从低位到高位切分成每组7bit,不足7bit的在高位用0填补。
- 由代表低位的组开始,为其加入最高位。如果这组是最后一组,则在最高位填上0,否则在最高位填上1。
- 将每一组转换为一个字节,字节的高4位和低4位分别对应十六进制数的一位。
- 将所有字节按照从低位组到高位组的顺序输出,字节之间用空格分隔。
解题思路:
- 使用vector<uint8_t>存储编码结果的字节。
- 对N进行循环处理,直到N为0:
- 取N的低7位,记为byte。
- 将N右移7位。
- 如果N不为0,说明还有更高位的字节,将byte的最高位设为1。
- 否则,将more标志设为false,表示已经处理完最后一个字节。
- 将byte添加到结果vector中。
- 遍历结果vector,输出每个字节的十六进制表示:
- 如果不是第一个字节,在前面添加一个空格。
- 以十六进制格式输出字节,使用大写字母,宽度为2,不足的在前面补0。
- 输出换行符。
C++代码实现:
#include <iostream>
#include <vector>
#include <iomanip>
using namespace std;void encodeVarint(uint64_t N) {vector<uint8_t> result;bool more = true;while (more) {uint8_t byte = N & 0x7F; // 取低7位N >>= 7;if (N != 0) {byte |= 0x80; // 不是最后一个字节,最高位填1} else {more = false; // 最后一个字节,最高位填0}result.push_back(byte);}for (size_t i = 0; i < result.size(); ++i) {if (i > 0) {cout << " ";}cout << hex << uppercase << setw(2) << setfill('0') << (int)result[i];}cout << endl;
}int main() {uint64_t N;cin >> N;encodeVarint(N);return 0;
}
代码解释:
encodeVarint函数接受一个无符号64位整数N,表示要编码的非负整数。- 定义
result为uint8_t类型的vector,用于存储编码结果的字节。 - 定义
more为布尔类型,初始值为true,表示是否还有更多字节需要处理。 - 进入循环,直到
more为false:- 取
N的低7位,记为byte。 - 将
N右移7位。 - 如果
N不为0,说明还有更高位的字节,将byte的最高位设为1。 - 否则,将
more标志设为false,表示已经处理完最后一个字节。 - 将
byte添加到resultvector中。
- 取
- 遍历
resultvector,输出每个字节的十六进制表示:- 如果不是第一个字节,在前面添加一个空格。
- 使用
hex、uppercase、setw(2)和setfill('0')控制输出格式,以十六进制格式输出字节,使用大写字母,宽度为2,不足的在前面补0。
- 输出换行符。
- 在
main函数中,读入无符号64位整数N,调用encodeVarint函数对N进行变长编码。
这个解答按照你提供的代码实现了变长编码,使用了C++标准库中的vector、iomanip等功能,并通过位运算和移位操作对整数进行处理。
解析2
#include <iostream>
#include <vector>
#include <iomanip>
#include <sstream>using namespace std;string encodeVarint(uint64_t N) {vector<uint8_t> result;bool more = true;while (more) {uint8_t byte = N & 0x7F; // 取低7位N >>= 7;if (N != 0) {byte |= 0x80; // 不是最后一个字节,最高位填1} else {more = false; // 最后一个字节,最高位填0}result.push_back(byte);}stringstream ss;for (size_t i = 0; i < result.size(); ++i) {if (i > 0) {ss << " ";}ss << hex << uppercase << setw(2) << setfill('0') << (int)result[i];}return ss.str();
}int main() {uint64_t N;cin >> N;string encodedString = encodeVarint(N);cout << encodedString << endl;return 0;
}解析3
#include <bits/stdc++.h>
using namespace std;long long n;
string a = "0123456789ABCDEF"; // 十六进制的数字void print(int i) { // 输出cout << a[i / 16] << a[i % 16] << " ";
}int main() {cin >> n;if (n == 0) {cout << "00";return 0;}vector<int> result;while (n > 0) {int k = n % 128; // 2^7=128,7位一截n /= 128;if (n > 0) {result.push_back(k + 128); // 判断是否为最高位} else {result.push_back(k);}}reverse(result.begin(), result.end()); // 逆序输出for (int byte : result) {print(byte);}return 0;
}相关文章:

B3870 [GESP202309 四级] 变长编码
[GESP202309 四级] 变长编码 题目描述 小明刚刚学习了三种整数编码方式:原码、反码、补码,并了解到计算机存储整数通常使用补码。但他总是觉得,生活中很少用到 2 31 − 1 2^{31}-1 231−1 这么大的数,生活中常用的 0 ∼ 100 0…...
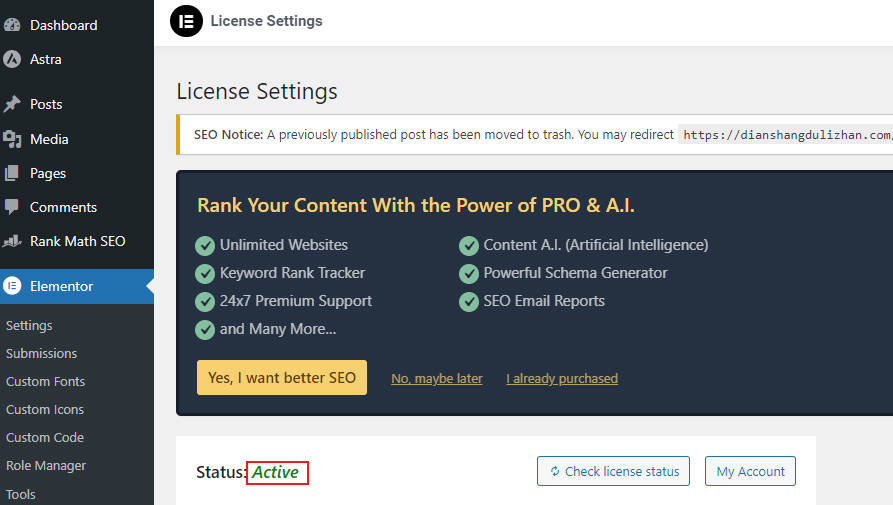
WordPress网站更换域名后如何重新激活elementor
在创建WordPress网站时,我们常常需要更改域名。但是,在更换域名后,你可能会遇到一个问题:WordPress后台中的Elementor插件授权状态会显示为不匹配。这时,就需要重新激活Elementor插件的授权。下面我会详细说明如何操作…...

linux cron 执行url
linux cron 执行url 在Linux中,你可以使用curl或wget来执行URL。如果你想要定期执行这个操作,可以使用cron来设置定时任务。 以下是一个使用curl在cron中执行URL的例子: 打开终端。 输入 crontab -e 命令来编辑你的cron作业。 添加一个新…...
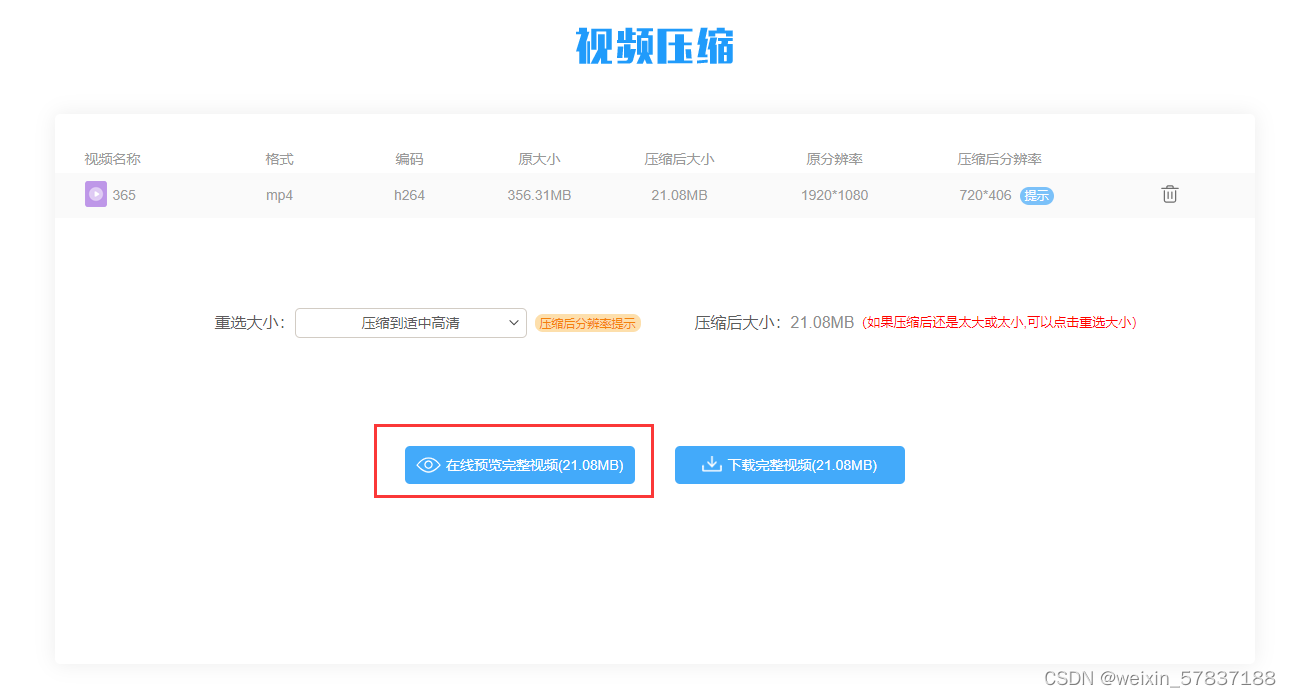
压缩视频在线压缩网站,压缩视频在线压缩工具软件
在数字化时代,视频成为了人们记录和分享生活的重要载体。然而,视频文件一般都非常大,这不仅占据了大量的存储空间,也给视频的传输和分享带来了不便。因此,压缩视频成为了许多人必须掌握的技能。本文将详细介绍如何压缩…...

linux经典例题编程
编写Shell脚本,计算1~100的和 首先vi 1.sh,创建一个名为1.sh的脚本,然后赋予这个脚本权限,使用命令chmod 755 1.sh,然后就可以在脚本中写程序,然后运行。 shell脚本内容 运行结果: 编写Shell脚本…...
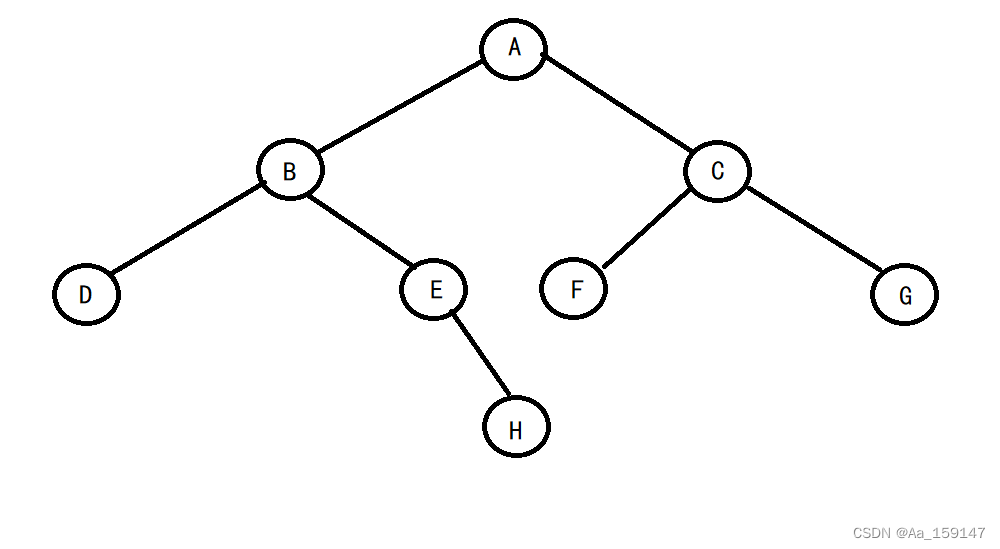
二叉树的实现(初阶数据结构)
1.二叉树的概念及结构 1.1 概念 一棵二叉树是结点的一个有限集合,该集合: 1.或者为空 2.由一个根结点加上两棵别称为左子树和右子树的二叉树组成 从上图可以看出: 1.二叉树不存在度大于2的结点 2.二叉树的子树有左右之分,次序不能…...
C++笔试强训day41
目录 1.棋子翻转 2.宵暗的妖怪 3.过桥 1.棋子翻转 链接https://www.nowcoder.com/practice/a8c89dc768c84ec29cbf9ca065e3f6b4?tpId128&tqId33769&ru/exam/oj (简单题)对题意进行简单模拟即可: class Solution { public:int dx[…...
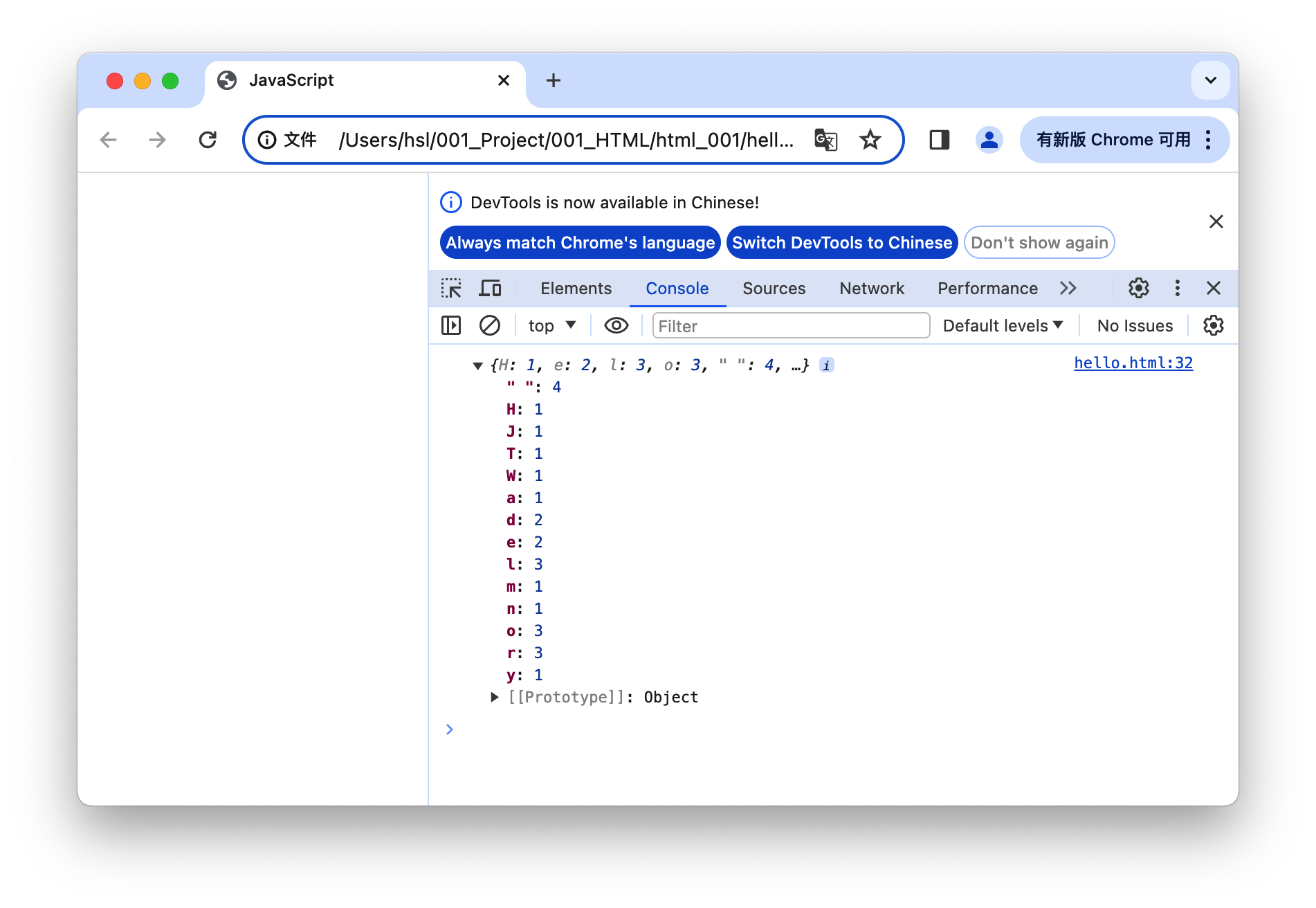
【JavaScript】内置对象 - 字符串对象 ⑤ ( 判断对象中是否有某个属性 | 统计字符串中每个字符出现的次数 )
文章目录 一、判断对象中是否有某个属性1、获取对象属性2、判定对象是否有某个属性 二、统计字符串中每个字符出现的次数1、算法分析2、代码示例 String 字符串对象参考文档 : https://developer.mozilla.org/zh-CN/docs/Web/JavaScript/Reference/Global_Objects/String 一、判…...

Linux环境下测试服务器的DDR5内存性能
要在Linux环境下测试服务器的DDR5内存性能,可以采用以下几种方法和工具: ### 测试原理 内存性能测试主要关注以下几个关键指标: - **带宽**:内存每秒能传输的数据量。 - **延迟**:内存访问请求从发出到完成所需的时间…...

19、matlab信号预处理中的中值滤波(medfilt1()函数)和萨维茨基-戈雷滤波滤(sgolayfilt()函数)
1、中值滤波:medfilt1()函数 说明:一维中值滤波 1)语法 语法1:y medfilt1(x) 将输入向量x应用3阶一维中值滤波器。 语法2:y medfilt1(x,n) 将一个n阶一维中值滤波器应用于x。 语法3:y medfilt1(x,n…...
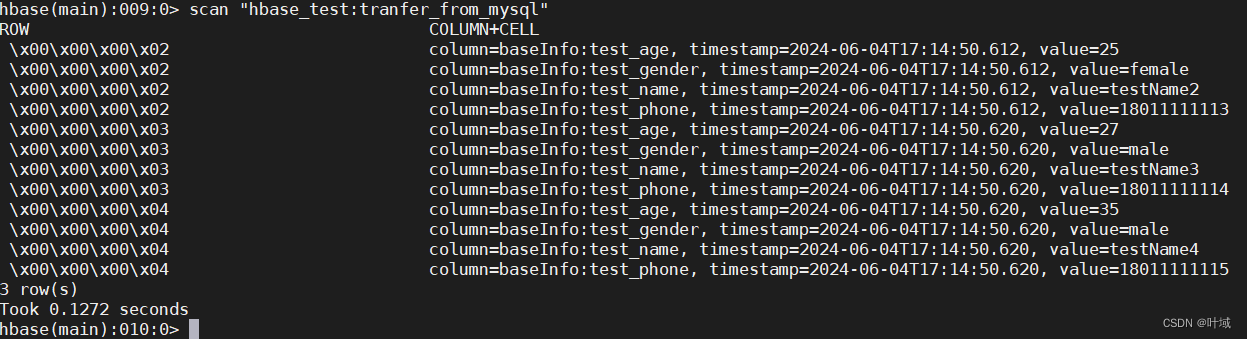
Scala 练习一 将Mysql表数据导入HBase
Scala 练习一 将Mysql表数据导入HBase 续第一篇:Java代码将Mysql表数据导入HBase表 源码仓库地址:https://gitee.com/leaf-domain/data-to-hbase 一、整体介绍二、依赖三、测试结果四、源码 一、整体介绍 HBase特质 连接HBase, 创建HBase执行对象 初始化…...

前端工程化:基于Vue.js 3.0的设计与实践
这里写目录标题 《前端工程化:基于Vue.js 3.0的设计与实践》书籍引言本书概述主要内容作者简介为什么选择这本书?结语 《前端工程化:基于Vue.js 3.0的设计与实践》书籍 够买连接—>https://item.jd.com/13952512.html 引言 在前端技术日…...
Linux☞进程控制
在终端执行命令时,Linux会建立进程,程序执行完,进程会被终止;Linux是一个多任务的OS,允许多个进程并发运行; Linxu中启动进程的两种途径: ①手动启动(前台进程(命令gedit)...后台进程(命令‘&’)) ②…...

mybatis离谱bug乱转类型
字符串传入的参数被转成了int: Param("online") String online<if test"online 0">and (heart_time is null or heart_time <![CDATA[ < ]]> UNIX_TIMESTAMP(SUBDATE(now(),INTERVAL 8 MINUTE)) )</if><if test"…...

视频监控管理平台LntonCVS视频汇聚平台充电桩视频监控应用方案
随着新能源汽车的广泛使用,公众对充电设施的安全性和可靠性日益重视。为了提高充电桩的安全管理和站点运营效率,LntonCVS公司推出了一套全面的新能源汽车充电桩视频监控与管理解决方案。 该方案通过安装高分辨率摄像头,对充电桩及其周边区域进…...

VS环境Python:深度探索与实用指南
VS环境Python:深度探索与实用指南 在编程领域,VS环境(Visual Studio环境)与Python的结合,为开发者们提供了一种强大而灵活的开发体验。这种结合不仅提升了开发效率,还增强了代码的可读性和可维护性。然而&…...
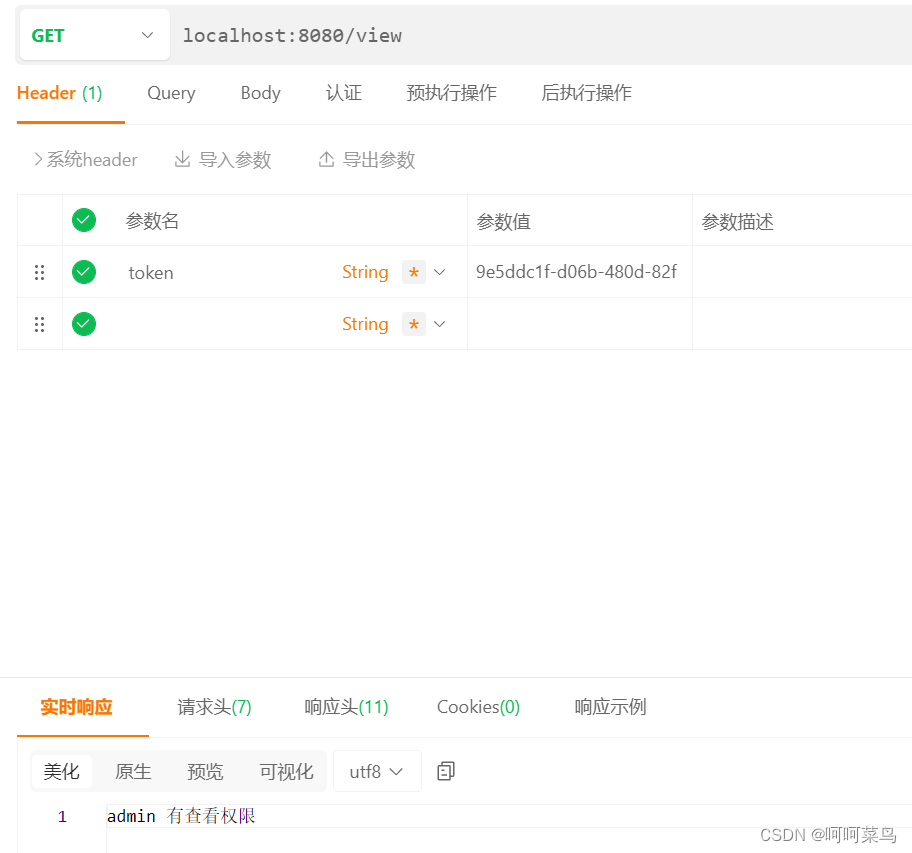
SpringBoot整合SpringSecurit(二)通过token进行访问
在文章:SpringBoot整合SpringSecurit(一)实现ajax的登录、退出、权限校验-CSDN博客 里面,使用的session的方式进行保存用户信息的,这一篇文章就是使用token的方式。 在其上进行的改造,可以先看SpringBoot…...

【算法训练 day50 打家劫舍、打家劫舍Ⅱ、打家劫舍Ⅲ】
目录 一、打家劫舍-LeetCode 198思路 二、打家劫舍Ⅱ-LeetCode 213思路 三.打家劫舍Ⅲ-LeeCode 337思路 一、打家劫舍-LeetCode 198 Leecode链接: leetcode 198 思路 dp数组含义为:当前数组范围下能偷到的最多的钱。递推公式为:dp[j] max(dp[j-2]nums[j],dp[j-1…...

YOLOv8改进 | 卷积模块 | 在主干网络中添加/替换蛇形卷积Dynamic Snake Convolution
💡💡💡本专栏所有程序均经过测试,可成功执行💡💡💡 蛇形动态卷积是一种新型的卷积操作,旨在提高对细长和弯曲的管状结构的特征提取能力。它通过自适应地调整卷积核的权重࿰…...
)
深入解析力扣183题:从不订购的客户(LEFT JOIN与子查询方法详解)
关注微信公众号 数据分析螺丝钉 免费领取价值万元的python/java/商业分析/数据结构与算法学习资料 在本篇文章中,我们将详细解读力扣第183题“从不订购的客户”。通过学习本篇文章,读者将掌握如何使用SQL语句来解决这一问题,并了解相关的复杂…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

论文阅读:LLM4Drive: A Survey of Large Language Models for Autonomous Driving
地址:LLM4Drive: A Survey of Large Language Models for Autonomous Driving 摘要翻译 自动驾驶技术作为推动交通和城市出行变革的催化剂,正从基于规则的系统向数据驱动策略转变。传统的模块化系统受限于级联模块间的累积误差和缺乏灵活性的预设规则。…...

STM32标准库-ADC数模转换器
文章目录 一、ADC1.1简介1. 2逐次逼近型ADC1.3ADC框图1.4ADC基本结构1.4.1 信号 “上车点”:输入模块(GPIO、温度、V_REFINT)1.4.2 信号 “调度站”:多路开关1.4.3 信号 “加工厂”:ADC 转换器(规则组 注入…...

goreplay
1.github地址 https://github.com/buger/goreplay 2.简单介绍 GoReplay 是一个开源的网络监控工具,可以记录用户的实时流量并将其用于镜像、负载测试、监控和详细分析。 3.出现背景 随着应用程序的增长,测试它所需的工作量也会呈指数级增长。GoRepl…...

Cursor AI 账号纯净度维护与高效注册指南
Cursor AI 账号纯净度维护与高效注册指南:解决限制问题的实战方案 风车无限免费邮箱系统网页端使用说明|快速获取邮箱|cursor|windsurf|augment 问题背景 在成功解决 Cursor 环境配置问题后,许多开发者仍面临账号纯净度不足导致的限制问题。无论使用 16…...
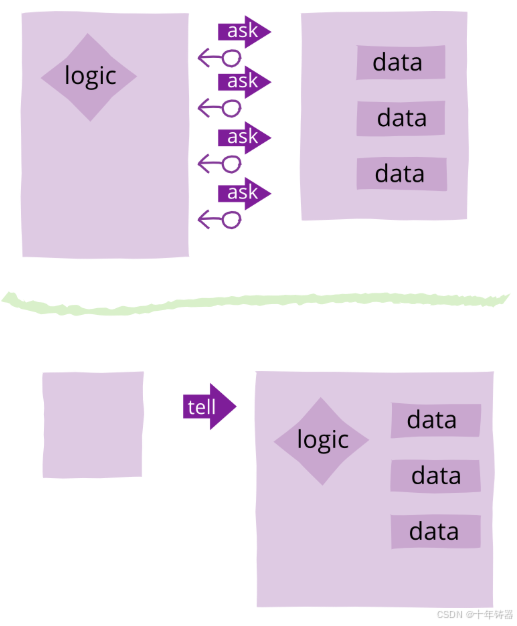
ABAP设计模式之---“Tell, Don’t Ask原则”
“Tell, Don’t Ask”是一种重要的面向对象编程设计原则,它强调的是对象之间如何有效地交流和协作。 1. 什么是 Tell, Don’t Ask 原则? 这个原则的核心思想是: “告诉一个对象该做什么,而不是询问一个对象的状态再对它作出决策。…...
