Numba 的 CUDA 示例(4/4):原子和互斥
本教程为 Numba CUDA 示例 第 4 部分。
本系列第 4 部分总结了使用 Python 从头开始学习 CUDA 编程的旅程
介绍
在本系列的前三部分(第 1 部分,第 2 部分,第 3 部分)中,我们介绍了 CUDA 开发的大部分基础知识,例如启动内核来执行高度并行的任务、利用共享内存执行快速缩减、将可重用逻辑封装为设备功能,以及如何使用事件和流来组织和控制内核执行。

在本节中
在本系列的最后一部分中,我们将介绍原子指令,这些指令允许我们安全地从多个线程对同一内存进行操作。我们还将学习如何利用这些操作来创建互斥锁,这是一种编码模式,允许我们“锁定”某个资源,以便每次只能由一个线程使用。
单击此处获取 Google colab 中的代码:https://colab.research.google.com/drive/1umKcslGW6gpynEfvk79i-jV08uB8_njc?usp=sharing
入门
导入并加载库,确保你有 GPU。
import warnings
from datetime import datetime
from time import perf_counterimport matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.ticker as ticker
import numpy as np
import requestsimport numba
from numba import cuda
from numba.core.errors import NumbaPerformanceWarning
from tqdm.auto import trangeprint(np.__version__)
print(numba.__version__)
print(mpl.__version__)# Ignore NumbaPerformanceWarning
warnings.simplefilter("ignore", category=NumbaPerformanceWarning)
---
1.25.2
0.59.1
3.7.1
cuda.detect()---
Found 1 CUDA devices
id 0 b'Tesla T4' [SUPPORTED]Compute Capability: 7.5PCI Device ID: 4PCI Bus ID: 0UUID: GPU-5569b5a1-ca7b-e1b7-79fc-851c80063714Watchdog: DisabledFP32/FP64 Performance Ratio: 32
Summary:1/1 devices are supported
True
原子
GPU 编程完全基于尽可能并行化相同的指令。对于许多 "令人尴尬的并行 "任务,线程不需要合作,也不需要使用其他线程使用的资源。其他模式,如还原,则通过算法设计确保同一资源只被一部分线程使用。在这种情况下,我们通过使用同步线程来确保所有其他线程都能及时更新。
在某些情况下,许多线程必须读取和写入同一个数组。如果试图同时进行读取或写入操作,就会出现问题。假设我们有一个内核,它将单个值递增 1。
# Example 4.1: A data race condition.
@cuda.jit
def add_one(x):x[0] = x[0] + 1
当我们使用线程单个块启动该内核时,我们将获得存储在输入数组中的值 1。
dev_val = cuda.to_device(np.zeros((1,)))add_one[1, 1](dev_val)
dev_val.copy_to_host()---
array([1.])
现在,如果我们启动 10 个区块,每个区块有 16 个线程,会发生什么情况?我们将 10 × 16 × 1 的总和存储到同一个内存元素中,因此我们希望 dev_val 中存储的值是 160。对吗?
dev_val = cuda.to_device(np.zeros((1,)))add_one[10, 16](dev_val)
dev_val.copy_to_host()---
array([1.])
实际上,我们的 dev_val 值不可能达到 160。为什么?因为线程会同时读写同一个内存变量!
下面是四个线程试图读写同一个全局存储器时可能发生的情况示意图。线程 1-3 在不同时间(分别为 t=0、2、2)从全局寄存器读取相同的 0 值。它们都递增 1,并在 t=4、7 和 8 时写回全局存储器。线程 4 的启动时间稍晚,为 t=5。此时,线程 1 已经写入全局存储器,因此线程 4 将读取 1 的值,并最终在 t=12 时将全局变量覆盖为 2。
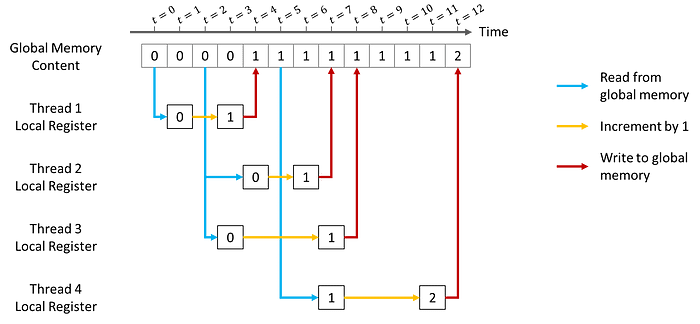
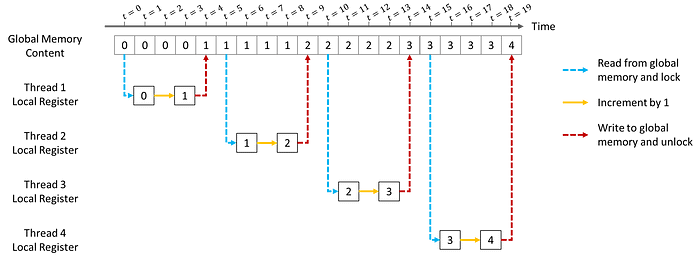
如果我们想得到最初预期的结果(如图 4.2 所示),就应该用原子操作代替非原子加法操作。原子操作将确保每次只由一个线程读/写内存。下面我们来详细谈谈原子操作。
# Example 4.2: An atomic add without race conditions.
@cuda.jit
def add_one_atomic(x):cuda.atomic.add(x, 0, 1) # Arguments are array, array index, value to adddev_val = cuda.to_device(np.zeros((1,)))add_one_atomic[10, 16](dev_val)
dev_val.copy_to_host()---
array([160.])
原子加法:计算直方图
为了更好地理解原子序数在哪里以及如何使用,我们将使用直方图计算。假设我们想计算某个文本中每个字母的数量。实现这一目的的简单算法是创建 26 个 “桶”,每个桶对应一个英文字母。然后,我们将遍历文本中的字母,每当遇到一个 “a”,我们就会将第一个 "桶 "递增一个,每当遇到一个 “b”,我们就会将第二个 "桶 "递增一个,以此类推。
在标准 Python 中,这些 "桶 "可以是字典,每个字典将一个字母与一个数字连接起来。由于我们喜欢在数组上进行 GPU 编程操作,因此我们将使用数组来代替。我们将使用全部 128 个 ASCII 字符,而不是 26 个字母。
在此之前,我们需要将字符串转换为 "数字 "数组。在这种情况下,将 UTF-8 字符串转换为 uint8 数据类型是合理的。
def str_to_array(x):return np.frombuffer(bytes(x, "utf-8"), dtype=np.uint8)def grab_uppercase(x):return x[65 : 65 + 26]def grab_lowercase(x):return x[97 : 97 + 26]my_str = "CUDA by Numba Examples"
my_str_array = str_to_array(my_str)---
array([ 67, 85, 68, 65, 32, 98, 121, 32, 78, 117, 109, 98, 97,32, 69, 120, 97, 109, 112, 108, 101, 115], dtype=uint8)
请注意,小写字母和大写字母的编码是不同的。因此,我们将使用几个实用功能来选择小写字母或大写字母。
此外,Numpy 已经提供了一个直方图函数,我们将用它来验证结果并比较运行时间。
histo_np, bin_edges = np.histogram(my_str_array, bins=128, range=(0, 128))np.testing.assert_allclose(bin_edges, np.arange(129)) # Bin edges are 1 more than binsdef plot_letter_histogram(hist, bin_edges, kind="percent", ax=None):width = 0.8start = bin_edges[0]stop = bin_edges[0] + hist.shape[0]if ax is None:ax = plt.gca()ax.bar(np.arange(start, stop), hist, width=width)ax.xaxis.set_major_locator(ticker.MultipleLocator(1))ax.xaxis.set_major_formatter(ticker.FuncFormatter(lambda x, pos: f"{int(x):c}"))ax.set(xlim=[start - width, stop - 1 + width], ylabel=kind.title())if kind == "count":ax.yaxis.set_major_formatter(ticker.FuncFormatter(lambda x, pos: f"{x:.0f}"))else:sum_hist = hist.sum()if kind == "probability":ax.yaxis.set_major_formatter(ticker.FuncFormatter(lambda x, pos: f"{x/sum_hist:.2f}"))else:ax.yaxis.set_major_formatter(ticker.FuncFormatter(lambda x, pos: f"{x/sum_hist:.0%}"))fig, axs = plt.subplots(1, 2, figsize=(10, 3), sharey=True)
plot_letter_histogram(grab_lowercase(histo_np), grab_lowercase(bin_edges), kind="count", ax=axs[0]
)
plot_letter_histogram(grab_uppercase(histo_np), grab_uppercase(bin_edges), kind="count", ax=axs[1]
)
axs[0].set(title="Lowercase")
axs[1].set(title="Uppercase");
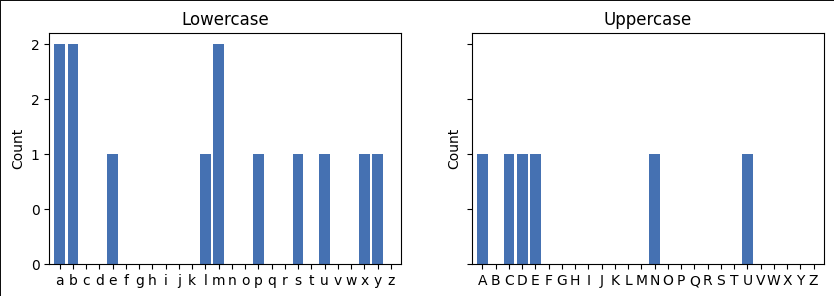
让我们自己编写 CPU 版本的函数,以了解其中的机制。
def histogram_cpu(arr):histo = np.zeros(128, dtype=np.int64)for char in arr:if char < 128:histo[char] += 1return histohisto_cpu = histogram_cpu(my_str_array)assert (histo_cpu - histo_np).sum() == 0 # Matches numpy version
由于每个 ASCII 字符都映射到 128 元素数组中的一个容器,我们需要做的就是找到它的容器并加 1,只要该容器在 0 到 127(包括 0 和 127)之内。
我们已经为第一个 GPU 版本做好了准备。
# Example 4.3: A GPU histogram
@cuda.jit
def kernel_histogram(arr, histo):i = cuda.grid(1)threads_per_grid = cuda.gridsize(1)for iarr in range(i, arr.size, threads_per_grid):if arr[iarr] < 128:cuda.atomic.add(histo, arr[iarr], 1)@cuda.jit
def kernel_zero_init(arr):i = cuda.grid(1)threads_per_grid = cuda.gridsize(1)for iarr in range(i, arr.size, threads_per_grid):arr[iarr] = 0threads_per_block = 128
blocks_per_grid = 32my_str_array_gpu = cuda.to_device(my_str_array)
histo_gpu = cuda.device_array((128,), dtype=np.int64)kernel_zero_init[1, 128](histo_gpu)
kernel_histogram[blocks_per_grid, threads_per_block](my_str_array_gpu, histo_gpu)
histo_cuda = histo_gpu.copy_to_host()太棒了!所以至少我们的函数是可以工作的。内核非常简单,并且具有与串行版本相同的结构。它以标准的 1D 网格步长循环结构开始,并且与串行版本不同,它使用原子添加。Numba 中的原子添加采用三个参数:将被递增的数组(histo)、将被递增的数组位置(arr[iarr],相当于串行版本中的 char),以及 histo[arr[iarr]] 将被递增的值(即本例中的 1)。
现在让我们加大赌注并将其应用于更大的数据集。
# Get the complete works of William Shakespeare
URL = "https://www.gutenberg.org/cache/epub/100/pg100.txt"
response = requests.get(URL)
str_bill = response.text
print(str_bill.split("\r")[0])---
The Project Gutenberg eBook of The Complete Works of William Shakespeare, by William Shakespeare
str_bill_array = np.frombuffer(bytes(str_bill, "utf-8"), dtype=np.uint8)
str_bill_array.size---
5638519
我们要处理的字符数约为 570 万个。让我们运行并记录迄今为止的三个版本。
histo_bill_np, _ = np.histogram(str_bill_array, bins=128, range=(0, 128))niter = 10
elapsed_np = 0.0
for i in trange(niter):tic = perf_counter()np.histogram(str_bill_array, bins=128, range=(0, 128))toc = perf_counter()elapsed_np += 1e3 * (toc - tic) # Convert to ms
elapsed_np /= niterniter = 2 # very slow!
elapsed_cpu = 0.0
for i in trange(niter):tic = perf_counter()histogram_cpu(str_bill_array)toc = perf_counter()elapsed_cpu += 1e3 * (toc - tic) # in ms
elapsed_cpu /= niterclass CUDATimer:def __init__(self, stream):self.stream = streamself.elapsed = None # in msdef __enter__(self):self.event_beg = cuda.event()self.event_end = cuda.event()self.event_beg.record(stream=self.stream)return selfdef __exit__(self, type, value, traceback):self.event_end.record(stream=self.stream)self.event_end.wait(stream=self.stream)self.event_end.synchronize()self.elapsed = self.event_beg.elapsed_time(self.event_end)threads_per_block = 128
blocks_per_grid = 32 * 80str_bill_array_gpu = cuda.to_device(str_bill_array)
histo_gpu = cuda.device_array((128,), dtype=np.int64)stream = cuda.stream()niter = 100
elapsed_gpu = 0.0
for i in trange(niter):kernel_zero_init[1, 128, stream](histo_gpu)with CUDATimer(stream=stream) as ct:kernel_histogram[blocks_per_grid, threads_per_block, stream](str_bill_array_gpu, histo_gpu)elapsed_gpu += ct.elapsed
elapsed_gpu /= niter
cuda.synchronize()fig, ax = plt.subplots()
rects = ax.bar(["NumPy", "Naive CPU", "GPU"],[elapsed_np / elapsed_gpu, elapsed_cpu / elapsed_gpu, elapsed_gpu / elapsed_gpu],
)
ax.bar_label(rects, padding=0, fmt="%.0fx")
ax.set(title="Performance relative to GPU version", ylabel="Times slower")
ax.yaxis.set_major_formatter(ticker.StrMethodFormatter("{x:.0f}x"))

以我们的 GPU 版本为基准,我们发现 NumPy 版本至少要慢 40 倍,而我们天真的 CPU 版本要慢数千倍。我们可以在几毫秒内处理这个 570 万字符的数据集,而传统的 CPU 解决方案则需要 10 多秒钟。这意味着我们有可能在几秒钟内处理 200 亿字符的数据集(如果我们有一个超过 20GB RAM 的 GPU),而我们最慢的版本需要一个多小时。因此,我们已经做得很不错了!
我们可以改进它吗?好吧,让我们重新审视一下这个内核的内存访问模式。
...
for iarr in range(i, arr.size, threads_per_grid):if arr[iarr] < 128:cuda.atomic.add(histo, arr[iarr], 1)
histo 是一个 128 元素的数组,位于 GPU 的全局内存中。在任何一个点上启动的每个线程都在尝试访问这个数组中的某些元素(即元素 arr[iarr])。因此,在任何一个点上,我们都有大约 128 × 32 × 80 = 327,680 个线程试图访问 128 个元素。因此,平均约有 32 × 80 = 2,560 个线程在竞争同一个全局内存地址。
为了缓解这种情况,我们在共享内存阵列中计算局部直方图。这是因为
- 共享阵列位于芯片上,因此读写速度更快
- 共享数组对于每个线程块来说都是本地的,因此只有较少的线程可以访问并因此争夺其资源。
信息:我们的计算假设字符是均匀分布的。请谨慎对待此类假设,因为自然数据集可能不符合这些假设。例如,自然语言文本中的大多数字符都是小写字母,因此我们将有 128 × 32 × 80 ÷ 26 ≈ 12,603 个线程竞争,而不是平均有 2,560 个线程竞争,这会带来更多问题!
# Example 4.4: A GPU histogram without as many memory conflicts
@cuda.jit
def kernel_histogram_shared(arr, histo):# Create shared array to hold local histogramhisto_local = cuda.shared.array((128,), numba.int64)histo_local[cuda.threadIdx.x] = 0 # initialize to zerocuda.syncthreads() # 确保同一块中的所有线程“注册”初始化i = cuda.grid(1)threads_per_grid = cuda.gridsize(1)for iarr in range(i, arr.size, threads_per_grid):if arr[iarr] < 128:cuda.atomic.add(histo_local, arr[iarr], 1) # 竞争相同内存的线程更少# 确保块中的所有线程都是最新的cuda.syncthreads()# 使用本地直方图的值更新全局内存直方图cuda.atomic.add(histo, cuda.threadIdx.x, histo_local[cuda.threadIdx.x])
之前有 2,560 个线程在竞争相同的内存,现在则有 2,560 ÷ 128 = 20 个线程。内核结束时,我们需要汇总所有本地结果。由于有 32 × 80 = 2,560 个区块,这意味着有 2,560 个线程在竞争写入全局内存。不过,我们确保每个线程只写一次,而之前我们必须写完输入数组的所有元素。
让我们看看新版本与旧版本的对比情况!
str_bill_array_gpu = cuda.to_device(str_bill_array)niter = 100
elapsed_gpu_shared = 0.0
for i in trange(niter):kernel_zero_init[1, 128, stream](histo_gpu)cuda.synchronize()with CUDATimer(stream=stream) as ct:kernel_histogram_shared[blocks_per_grid, threads_per_block, stream](str_bill_array_gpu, histo_gpu)elapsed_gpu_shared += ct.elapsed
elapsed_gpu_shared /= niter
cuda.synchronize()fig, ax = plt.subplots()
rects = ax.bar(["NumPy", "Naive GPU", "GPU"],[elapsed_np / elapsed_gpu_shared,elapsed_gpu / elapsed_gpu_shared,elapsed_gpu_shared / elapsed_gpu_shared,],
)
ax.bar_label(rects, padding=0, fmt="%.1fx")
ax.set(title="Performance relative to improved GPU version", ylabel="Times slower")
ax.yaxis.set_major_formatter(ticker.StrMethodFormatter("{x:.0f}x"))

因此,这比原始版本提高了约 3 倍!
我们将块数设置为 32 × SM 数量的倍数,如上一个教程中建议的那样。但是哪个倍数呢?让我们来计算一下!
threads_per_block = 128
elapsed_conflict = []
elapsed_shared = []block_range = range(10, 1000, 5)
histo_gpu = cuda.device_array((128,), np.int64, stream=stream)
for i in trange(block_range.start, block_range.stop, block_range.step):blocks_per_grid = 32 * ielapsed1 = 0.0elapsed2 = 0.0niter = 50for i in range(niter):kernel_zero_init[1, 128, stream](histo_gpu)with CUDATimer(stream) as ct1:kernel_histogram[blocks_per_grid, threads_per_block, stream](str_bill_array_gpu, histo_gpu)elapsed1 += ct1.elapsedkernel_zero_init[1, 128, stream](histo_gpu)with CUDATimer(stream) as ct2:kernel_histogram_shared[blocks_per_grid, threads_per_block, stream](str_bill_array_gpu, histo_gpu)elapsed2 += ct2.elapsedelapsed_conflict.append(elapsed1 / niter)elapsed_shared.append(elapsed2 / niter)fastest_sm_conflict = list(block_range)[np.argmin(elapsed_conflict)]
fastest_sm_shared = list(block_range)[np.argmin(elapsed_shared)]fig, ax = plt.subplots()
ax.plot(block_range, elapsed_conflict, color="C0")
ax.axvline(fastest_sm_conflict, ls="--", color="C0")
ax.yaxis.label.set_color("C0")
ax.tick_params(axis="y", colors="C0")
ax.set(ylabel="Time of conflicted version [ms]")ax2 = ax.twinx()
ax2.plot(block_range, elapsed_shared, color="C3")
ax2.axvline(fastest_sm_shared, ls="--", color="C3")
ax2.yaxis.label.set_color("C3")
ax2.tick_params(axis="y", colors="C3")
ax2.set(ylabel="Time of shared version [ms]");
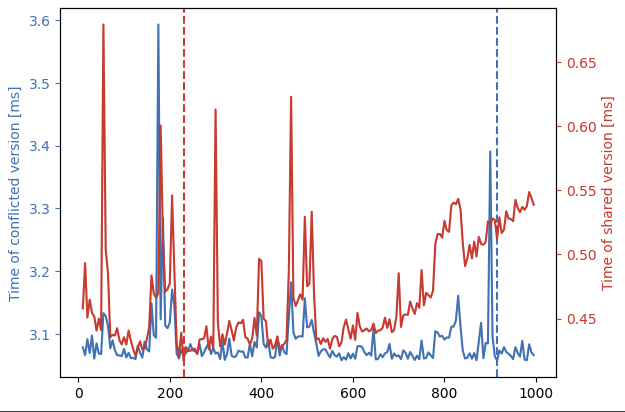
有两点:首先,我们需要两个轴来显示数据,因为原始版本(蓝色)的速度要慢得多。其次,垂直线显示对于某个函数来说,最佳的 SM 数量是多少。最后,虽然原始版本不会随着添加更多块而变得更糟,但共享版本并非如此。要理解为什么会这样,请记住共享数组版本有两个部分
- 第一部分,少数线程竞争相同(快速)内存(共享数组部分)。
- 第二部分,许多线程竞争相同的(慢速)内存(最后的原子添加)。
随着更多块的添加,在简单版本中,它很快就会遇到瓶颈,而且情况不会变得更糟,而在共享阵列版本中,第一部分的竞争保持不变,但第二部分的竞争会增加。另一方面,太少的块不会产生足够的并行化(对于任何一个版本而言)。上图找到了这两个极端之间的“最佳点”。
使用互斥锁锁定资源
在前面的例子中,我们使用了整数值的原子加法运算来锁定某些资源,并确保一次只有一个线程控制它们。加法不是唯一的原子操作,也不必应用于整数值。Numba CUDA 支持对整数和浮点数的各种原子操作。但曾几何时(CUDA 计算 1.x),浮点原子并不存在。因此,如果我们想使用浮点数的原子来编写一个归约,我们就需要另一个结构。
虽然现在原子确实支持浮点数,但允许我们应用任意原子操作的“互斥”代码模式在某些情况下仍然有用。
mutex,即互斥锁,是一种向试图访问某个资源的其他线程发出信号,表明该资源是否可用。可以使用可以采用两个值的变量来创建互斥锁:
- 0:🟢 绿灯,继续使用特定内存/资源
- 1:🔴 红灯,停止,请勿尝试使用/访问某个内存/资源
要锁定内存,应该将 1 写入互斥锁,要解锁,应该写入 0。但需要小心,如果将互斥锁(非原子性地)写入,其他线程可能正在访问该资源,至少会创建错误的值,甚至更糟的是,造成死锁。另一个问题是,只有在之前未锁定的情况下才能锁定互斥锁。因此,在写入 1(锁定)之前,我们需要读取互斥锁并确保其为 0(解锁)。CUDA 提供了一种特殊操作来原子地执行这两件事:atomicCAS。在 Numba CUDA 中,它更明确地命名为:
cuda.atomic.compare_and_swap(array, old, val)
如果 array[0] 的当前值等于 old(这是“比较”部分),则此函数将仅以原子方式分配val给array[0](这是“交换”部分);否则它现在将交换。此外,它以原子方式返回 array[0] 的当前值。因此,要锁定互斥锁,我们可以使用:
cuda.atomic.compare_and_swap(mutex, 0, 1)
因此,我们只会在 unlocked(0) 时分配一个 lock(1)。上面这行代码的一个问题是,如果线程到达它并读取到 1(锁定),它就会继续执行,这可能不是我们想要的。我们理想情况下希望线程停止执行,直到我们可以锁定互斥锁。因此,我们改为执行以下操作:
while cuda.atomic.compare_and_swap(mutex, 0, 1) != 0:pass
在这种情况下,线程将一直持续,直到它能够正确锁定线程。假设线程到达先前锁定的互斥锁,其当前值为 1。因此,我们首先注意到,compare_and_swap无法锁定它, 因为 curr = 1 != old = 0。它也不会退出while循环,因为当前值 1 与 0(while 条件)不同。它将一直停留在这个循环中,直到它最终能够读取当前值为 0 的未锁定互斥锁。在这种情况下,它还将能够将 1 分配给互斥锁,因为curr = 0 == old = 0。
要解锁,我们只需原子地为互斥锁分配一个 0。我们将使用
cuda.atomic.exch(array, idx, val)
它只是原子赋值 array[idx] = val,返回 array[idx] 的旧值(原子加载)。由于我们不会使用这个函数的返回值,在这种情况下,你可以把它看作是一个原子赋值(即 atomic_add(array, idx, val) 对 array[idx] += val 的赋值与 exch(array, idx, val) 对 array[idx] = val 的赋值一样)。
现在我们有了锁定和解锁机制,让我们重试原子“加一”,但使用互斥锁。
# Example 4.5: An atomic add with mutex.
@cuda.jit(device=True)
def lock(mutex):while cuda.atomic.compare_and_swap(mutex, 0, 1) != 0:passcuda.threadfence()@cuda.jit(device=True)
def unlock(mutex):cuda.threadfence()cuda.atomic.exch(mutex, 0, 0)@cuda.jit
def add_one_mutex(x, mutex):lock(mutex) # 线程将在此停止,直到它们可以自动读取 0 互斥,此时他们将自动向其写入 1x[0] += 1 # 一次只有一个线程会访问该资源,其他所有线程将在上面的队列中等待unlock(mutex) # 线程原子地将 0 写入互斥锁,并释放它,所有其他线程都在尝试获取锁dev_val = cuda.to_device(np.zeros((1,)))
mutex = cuda.to_device(np.zeros((1,), dtype=np.int64))add_one_mutex[10, 16](dev_val, mutex)
dev_val.copy_to_host()---
array([160.])
上面的代码非常简单,我们有一个内核,它可以锁定线程的执行,直到它们自己可以获得解锁的互斥。此时,它们将更新 x[0] 的值并解锁互斥。任何时候都不会有多个线程读取或写入 x[0],从而实现了原子性!
上述代码中只有一个细节我们没有涉及,那就是 cuda.threadfence() 的使用。本例中并不需要它,但它能确保锁定和解锁机制的正确性。我们很快就会知道原因!
互斥点乘
在本系列的第 2 部分中,我们学习了如何在 GPU 中应用缩减。我们使用它们来计算数组的总和。我们的代码不够优雅的一点是,我们将部分求和留给了 CPU。我们当时缺乏的是应用原子操作的能力。
我们将该示例重新解释为点乘,但这次是将求和进行到底。这意味着我们不会返回 "部分 "点乘,而是通过使用 mutex 在 GPU 中使用原子求和。首先,让我们将 reduce 重新解释为点乘:
threads_per_block = 256
blocks_per_grid = 32 * 20# Example 4.6: A partial dot product
@cuda.jit
def dot_partial(a, b, partial_c):igrid = cuda.grid(1)threads_per_grid = cuda.gridsize(1)s_thread = 0.0for iarr in range(igrid, a.size, threads_per_grid):s_thread += a[iarr] * b[iarr]s_block = cuda.shared.array((threads_per_block,), numba.float32)tid = cuda.threadIdx.xs_block[tid] = s_threadcuda.syncthreads()i = cuda.blockDim.x // 2while i > 0:if tid < i:s_block[tid] += s_block[tid + i]cuda.syncthreads()i //= 2# 此行以上的代码在下一个版本中将保持完全相同if tid == 0:partial_c[cuda.blockIdx.x] = s_block[0]# Example 4.6: A full dot product with mutex
@cuda.jit
def dot_mutex(mutex, a, b, c):igrid = cuda.grid(1)threads_per_grid = cuda.gridsize(1)s_thread = 0.0for iarr in range(igrid, a.size, threads_per_grid):s_thread += a[iarr] * b[iarr]s_block = cuda.shared.array((threads_per_block,), numba.float32)tid = cuda.threadIdx.xs_block[tid] = s_threadcuda.syncthreads()i = cuda.blockDim.x // 2while i > 0:if tid < i:s_block[tid] += s_block[tid + 1]cuda.syncthreads()i //= 2# 我们没有将部分归约分配给全局内存数组,而是将自动将其添加到 c[0]。if tid == 0:lock(mutex)c[0] += s_block[0]unlock(mutex)N = 10_000_000
a = np.ones(N, dtype=np.float32)
b = (np.ones(N) / N).astype(np.float32)dev_a = cuda.to_device(a)
dev_b = cuda.to_device(b)
dev_c = cuda.device_array((1,), dtype=a.dtype)
dev_partial_c = cuda.device_array((blocks_per_grid,), dtype=a.dtype)
dev_mutex = cuda.device_array((1,), dtype=np.int32)dot_partial[blocks_per_grid, threads_per_block](dev_a, dev_b, dev_partial_c)
dev_partial_c.copy_to_host().sum()---
0.9999999
kernel_zero_init[1, 1](dev_c)
dot_mutex[blocks_per_grid, threads_per_block](dev_mutex, dev_a, dev_b, dev_c)
dev_c.copy_to_host().item()---
1.0000088214874268
一切顺利!
在结束之前,我答应过要重温一下 cuda.threadfence。
摘自 CUDA “圣经”(B.5.内存栅栏函数):
__threadfence()ensures that no writes to all memory made by the calling thread after the call to__threadfence()are observed by any thread in the device as occurring before any write to all memory made by the calling thread before the call to__threadfence().
尝试翻译一下:
__threadfence()确保调用线程在调用__threadfence()之后对所有内存的写入操作,不会被设备中任何线程视为发生在调用__threadfence()的任何写入操作之前。
如果我们在解锁互斥锁之前忽略线程隔离,那么即使使用原子操作,我们也可能会读取过时的信息,因为其他线程可能尚未写入内存。同样,在解锁之前,我们必须确保更新内存引用。这一切都不明显,而且早在2015 年 Alglave等人首次提出之前就已经存在了。最终,此修复程序发布在 CUDA by Examples 的勘误表中,这启发了本系列教程。
小结
在本系列的最后一篇教程中,你学习了如何使用原子操作,这是协调线程的一个基本要素。你还学习了互斥模式,该模式利用原子来创建自定义区域,每次只有一个线程可以访问这些区域。
最后:
在本系列的四期中,我们涵盖了足够的内容,让你能够在各种常见情况下使用 Numba CUDA。这些教程并非详尽无遗,旨在介绍和激发读者对 CUDA 编程的兴趣。
我们尚未涉及的一些主题包括:动态并行(让内核启动内核)、复杂同步(例如,warp 级别、协作组)、复杂内存隔离(我们上面提到过)、多 GPU、纹理和许多其他主题。其中一些目前不受 Numba CUDA 支持,其中一些被认为对于入门教程来说太高级了。
为了进一步提高你的 CUDA 技能,强烈推荐《CUDA C++ 编程指南》以及Nvidia 博客文章。
在 Python 生态系统中,需要强调的是,除了 Numba 之外,还有许多可以利用 GPU 的解决方案。而且它们大多可以互操作,因此不必只选择一个。PyCUDA, CUDA Python, RAPIDS, PyOptix, CuPy 和 PyTorch是正在积极开发的库的示例。
相关文章:

Numba 的 CUDA 示例(4/4):原子和互斥
本教程为 Numba CUDA 示例 第 4 部分。 本系列第 4 部分总结了使用 Python 从头开始学习 CUDA 编程的旅程 介绍 在本系列的前三部分(第 1 部分,第 2 部分,第 3 部分)中,我们介绍了 CUDA 开发的大部分基础知识…...

【机器学习】机器学习引领AI:重塑人类社会的新纪元
📝个人主页🌹:Eternity._ 🌹🌹期待您的关注 🌹🌹 ❀机器学习引领AI 📒1. 引言📕2. 人工智能(AI)🌈人工智能的发展🌞应用领…...

【制作面包game】
编写一个制作面包的游戏代码涉及到游戏设计、编程和用户界面设计等多个方面。这里我可以提供一个简化版本的Python代码示例,用于创建一个基本的面包制作游戏。这个游戏将会有一个简单的用户界面,玩家可以通过输入命令来制作面包。 游戏的基本流程如下&a…...

Django更改超级用户密码
Django更改超级用户密码 1、打开shell 在工程文件目录下敲入: python manage.py shell再在python交互界面输入: from django.contrib.auth.models import User user User.objects.get(username root) user.set_password(123456) user.save()其中ro…...

ROS基础学习-ROS通信机制进阶
ROS通信机制进阶 目录 0.简介1.常用API1.1 节点初始化函数1.1.1 C++1.1.2 Python1.2 话题与服务相关函数1.2.1 对象获取相关1.2.1.1 C++1.2.1.2 Python1.2.2 订阅对象相关1.2.2.1 C++1.2.2.2 Python1.2.3 服务对象相关函数1.2.3.1 C++1.2.3.2 Python1.2.4 客户端对象相关1.2.4.…...
 and shallowReadonly())
【Vue3】shallowReactive() and shallowReadonly()
历史小剧场 所谓历史,就是过去的事,它的残酷之处在于:无论你哀嚎,悲伤,痛苦,落寞,追悔,它都无法改变。 一具有名的尸体躺在无数无名的尸体上,这就是所谓的霸业。---- 《明…...
【javaEE初阶】
🌈🌈🌈关于java ⚡⚡⚡java的由来 我们这篇文章主要是来介绍javaEE,一般称为java企业版,实际上java的历史可以追溯到上个世纪90年代,当时主要的语言主流的还是C语言和C,但是在那个时期嵌入式初…...
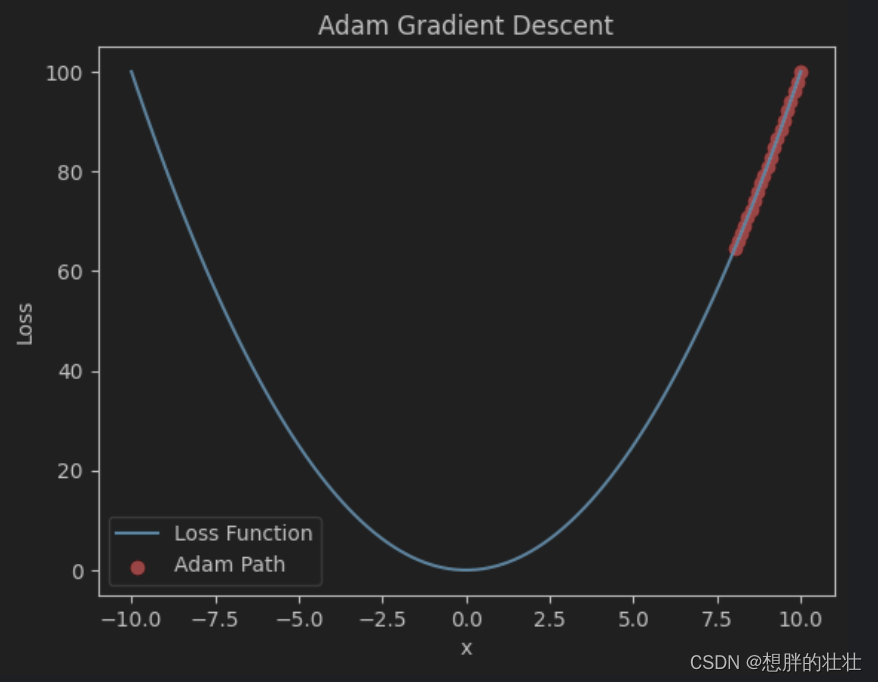
深度学习 - 梯度下降优化方法
梯度下降的基本概念 梯度下降(Gradient Descent)是一种用于优化机器学习模型参数的算法,其目的是最小化损失函数,从而提高模型的预测精度。梯度下降的核心思想是通过迭代地调整参数,沿着损失函数下降的方向前进&#…...
Steam下载游戏很慢?一个设置解决!
博主今天重装系统后,用steam下载发现巨慢 500MB,都要下载半小时。 平时下载软件,一般1分钟就搞定了,于是大致就知道,设置应该出问题了 于是修改了,如下设置之后,速度翻了10倍。 如下&#x…...

51单片机采用定时器T1的方式1的中断计数方式,外接开关K4按4次后,8只LED闪烁不停
1、功能描述 采用定时器T1的方式1的中断计数方式,外接开关K4按4次后,8只LED闪烁不停 2、实验原理 定时器原理:8051的定时器可以用于计数外部事件或执行内部定时操作。在本程序中,定时器1被设置为模式2,即8位自动重装载定时器模式…...

windows系统 flutter 开发环境配置
1、管理员运行powershell,安装:Chocolatey 工具,粘贴复制运行下列脚本: Chocolatey 官方安装文档 Set-ExecutionPolicy Bypass -Scope Process -Force; [System.Net.ServicePointManager]::SecurityProtocol [System.Net.ServicePointManage…...
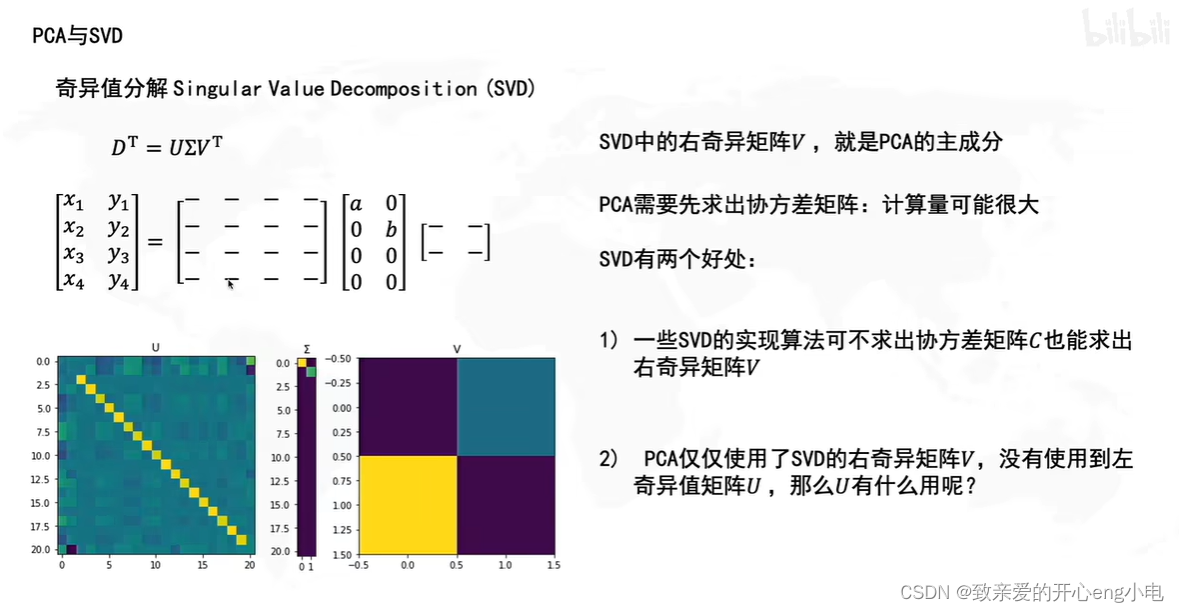
【线性代数】SVDPCA
用最直观的方式告诉你:什么是主成分分析PCA_哔哩哔哩_bilibili 奇异值分解singular value decomposition,SVD principal component analysis,PCA 降维操作 pca就是降维后使得信息损失最小 投影在坐标轴上的点越分散,信息保留越多 pca的实现…...

1.Vue2使用ElementUI-初识及环境搭建
目录 1.下载nodejs v16.x 2.设置淘宝镜像源 3.安装脚手架 4.创建一个项目 5.项目修改 代码地址:source-code: 源码笔记 1.下载nodejs v16.x 下载地址:Node.js — Download Node.js 2.设置淘宝镜像源 npm config set registry https://registry.…...
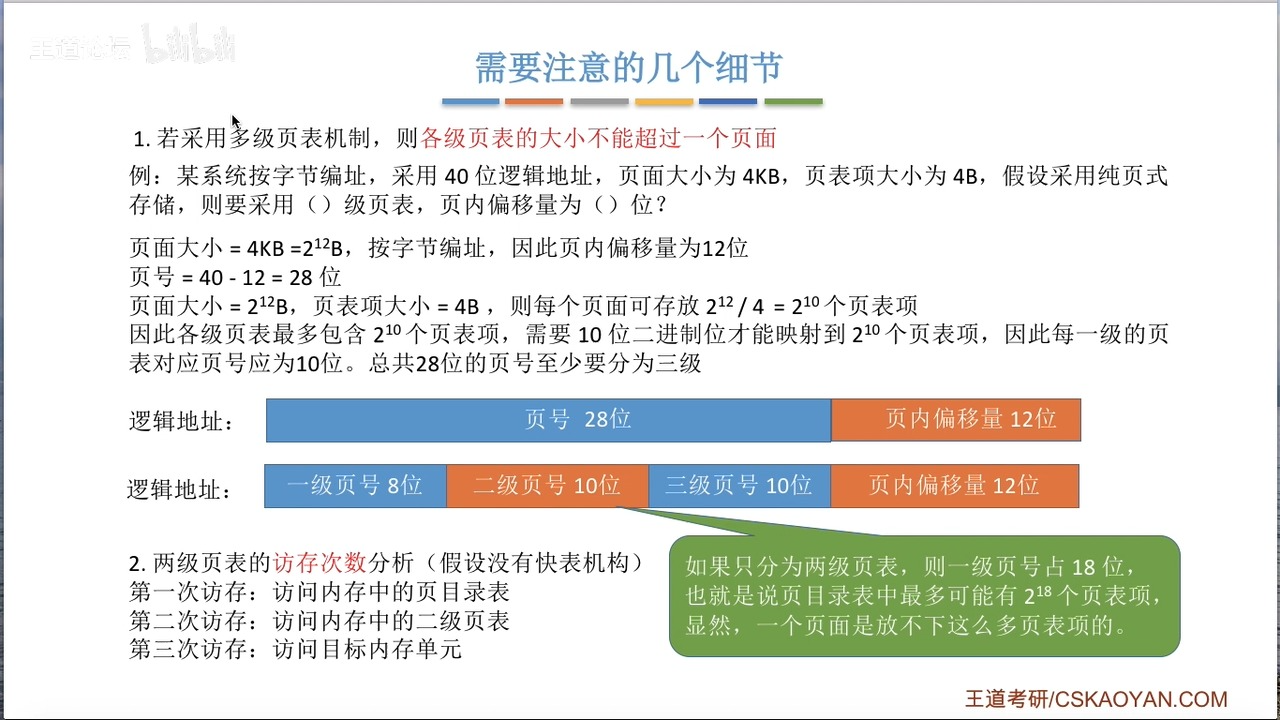
OS复习笔记ch7-3
承接上文我们讲完了页式管理和段式管理,接下来让我们深入讲解一下快表和二级页表 快表 快表和计算机组成原理讲的Cache原理如出一辙。为了减少访存的次数,OS在访问页面的时候创建了快表(Translation Lookaside Buffer ,简称TLB&…...
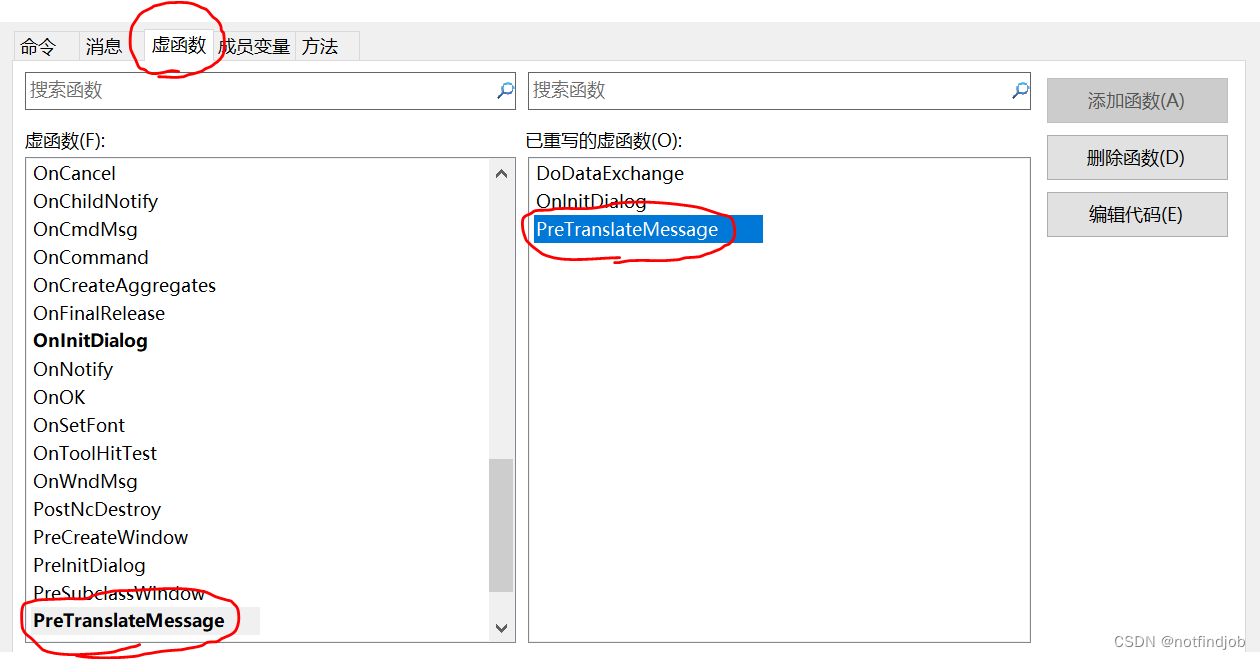
MFC 教程-回车时窗口退出问题
【问题描述】 MFC窗口默认时,按回车窗口会退出 【原因分析】 默认调用OnOK() 【解决办法】 重写虚函PreTranslateMessage BOOL CTESTMFCDlg::PreTranslateMessage(MSG* pMsg) {// TODO: 在此添加专用代码和/或调用基类// 修改回车键的操作反应 if (pMsg->…...
CTFHUB-SQL注入-字符型注入
目录 查询数据库名 查询数据库中的表名 查询表中数据 总结 此题目和上一题相似,一个是整数型注入,一个是字符型注入。字符型注入就是注入字符串参数,判断回显是否存在注入漏洞。因为上一题使用手工注入查看题目 flag ,这里就不…...

Docker配置Redis集群以及主从扩容与缩容
基础镜像拉取 docker run -p 6379:6379 -d redis:6.0.8 配置文件以及数据卷挂载 # 开启密码验证(可选) requirepass 1234 # 允许redis外地连接,需要注释掉绑定的IP # bind 127.0.0.1 # 关闭保护模式(可选) protected-m…...

【计算机网络】 传输层
一、传输层提供的服务 1.1 传输层的功能 1.1.1 传输层的功能如下: 传输层提供应用进程之间的逻辑通信(即端到端的通信)。与网络层的区别是:网络层提供的是主机之间的逻辑通信。 1.1.2 复用和分用 传输层要还要对收到的报文进行…...

山东大学软件学院项目实训-创新实训-基于大模型的旅游平台(二十七)- 微服务(7)
11.1 : 同步调用的问题 11.2 异步通讯的优缺点 11.3 MQ MQ就是事件驱动架构中的Broker 安装MQ docker run \-e RABBITMQ_DEFAULT_USERxxxx \-e RABBITMQ_DEFAULT_PASSxxxxx \--name mq \--hostname mq1 \-p 15672:15672 \-p 5672:5672 \-d \rabbitmq:3-management 浏览器访问1…...

Java Web应用,IPv6问题解决
在Java Web程序中,如果使用Tomcat并遇到了IPv6相关的问题,可以通过以下几种方式来解决: 1. 配置Tomcat以使用IPv4 默认情况下,Java可能会优先使用IPv6。如果你希望Tomcat使用IPv4,最简单的方法是通过设置系统属性来强…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Chromium 136 编译指南 Windows篇:depot_tools 配置与源码获取(二)
引言 工欲善其事,必先利其器。在完成了 Visual Studio 2022 和 Windows SDK 的安装后,我们即将接触到 Chromium 开发生态中最核心的工具——depot_tools。这个由 Google 精心打造的工具集,就像是连接开发者与 Chromium 庞大代码库的智能桥梁…...

Rust 开发环境搭建
环境搭建 1、开发工具RustRover 或者vs code 2、Cygwin64 安装 https://cygwin.com/install.html 在工具终端执行: rustup toolchain install stable-x86_64-pc-windows-gnu rustup default stable-x86_64-pc-windows-gnu 2、Hello World fn main() { println…...
