详解linux设备下的/dev/null

/dev/zero是一个特殊的设备文件,它在Linux系统中通常被用来生成无限数量的零数据流。
这个设备文件位于/dev目录下,它不代表任何实际的硬件设备,而是一个虚拟设备。
当从/dev/zero设备中读取数据时,会得到无限数量的零字节,这些字节的值都是0。
因此,/dev/zero常用于生成大量的零数据流,例如在创建文件时初始化数据、进行测试或者模拟特定场景。
常见用法包括:
数据初始化: 在创建文件时,可以使用dd命令从/dev/zero读取数据,并写入到文件中,以初始化文件内容为零或者特定值。
测试用途: 在进行一些性能测试或者功能测试时,可能需要生成大量的零数据流,这时可以使用/dev/zero设备来生成数据。
随机数生成: /dev/zero的姊妹设备/dev/random和/dev/urandom用于生成随机数,而/dev/zero则生成确定性的零数据流。
/dev/zero设备是Linux系统中的一个非常有用的工具,可以方便地生成大量的零数据流,用于各种目的,从数据初始化到测试都有很多应用场景。
相关文章:

详解linux设备下的/dev/null
/dev/zero是一个特殊的设备文件,它在Linux系统中通常被用来生成无限数量的零数据流。 这个设备文件位于/dev目录下,它不代表任何实际的硬件设备,而是一个虚拟设备。 当从/dev/zero设备中读取数据时,会得到无限数量的零字节&…...

GPT-4 Turbo 和 GPT-4 的区别
引言 人工智能(AI)领域的发展日新月异,OpenAI 的 GPT 系列模型一直是这一领域的佼佼者。GPT-4 和 GPT-4 Turbo 是目前市场上最先进的语言模型之一。本文将详细探讨 GPT-4 和 GPT-4 Turbo 之间的区别,以帮助用户更好地理解和选择适…...

基于小波多分辨分析的一维时间序列信号趋势检测与去除(MATLAB R2018a)
小波最开始是数学上提出的概念,并且在纯数学的王国里存在了一个世纪之久。最开始是为了弥补傅里叶分析的缺陷,即傅里叶级数发散的问题,并寻找出能够代替傅里叶分析的方法。从最早的一些艰难的探索开始直到慢慢发展成为一套完整系统的小波分析…...

Linux RedHat7.6操作系统的xfs格式化后,mount不生效
Linux RedHat7.6操作系统的xfs格式化后,mount不生效 问题现象 最近在准备测试环境的过程中,当对xfs文件系统格式化后,mount磁盘,通过df -h命令查看,未显示挂载磁盘信息 [rootZHZXLxjspo0db003 ~]# mount /dev/datavg/datavg-lv_data /data…...

高并发ping多台主机IP
简介 社区或者是大型公司往往有成千上万或者几百台设备,保持设备始终在线对网络运维人员来说至关重要,然而一个一个登录检查,或者一个一个ping并不明智,累人且效率极低,并出错率高。花钱买检测服务当我没说。 shell编…...

03 Linux 内核数据结构
Linux kernel 有四种重要的数据结构:链表、队列、映射、二叉树。普通驱动开发者只需要掌握链表和队列即可。 链表和队列 Linux 内核都有完整的实现,我们不需要深究其实现原理,只需要会使用 API 接口即可。 1、链表 链表是 Linux 内核中最简单、最普通的数据结构。链表是一…...

关于软件调用独显配置指引【笔记】
关于笔记本电脑不支持独显直连的,bios下也是没有切换独显直连的选项的,处理方法 简单的来说按照图片指引可配置让软件调用独显: 1、进入系统→屏幕→显示卡界面; 2、【添加应用】浏览需要调用独显的软件安装目录,并打开…...

正大国际期货:什么是主力合约?
一个期货品种,在同一时间段,会上市多个月份的合约, 由于主力合约交易量大,流动性高,一般建议新手交易主力合约。 主力合约通常指交易集中,流动性好的合约 ,即在一段时间内交易量和持仓量最大的…...

codeforces round 949 div2
A Turtle and Piggy Are Playing a Game 题目: 思路:输出2的幂次b使得2^b为最大的不超过x的数 代码: #include <iostream>using namespace std;const int N 2e5 10;void solve() {int l, r;cin >> l >> r;if(r % 2) …...

分享美好,高清无阻 - 直播极简联网解决方案
1、需求背景 随着移动互联网、UGC模式和直播平台的发展,网络直播的门槛日益降低,越来越多的人希望成为直播的主角。基于物联网的户外直播无线联网解决方案应运而生,满足直播者的需求。 户外直播无线联网解决方案提供了无处不在的直播体验&a…...

贪心算法-加油站
一、题目描述 二、解题思路 1.运动过程分析 这里需要一个油箱剩余油量的变量resGas,初始化resGas0;还需要一个标记从什么位置当做初始位置的startIdx,初始化startIdx0。 我们从数组下标idx0处开始向后遍历,初始时startIdx0&#…...
)
【ArcGIS微课1000例】0116:将度-分-秒值转换为十进制度值(字段计算器VBA)
相关阅读:【ArcGIS微课1000例】0087:经纬度格式转换(度分秒转度、度转度分秒) 文章目录 一、计算方法二、计算案例一、计算方法 将度分秒转换为十进制度的简单等式: DD = (Seconds/3600) + (Minutes/60) + Degrees如果角度值是负数,则转换方法不同。其中一种方法是: …...
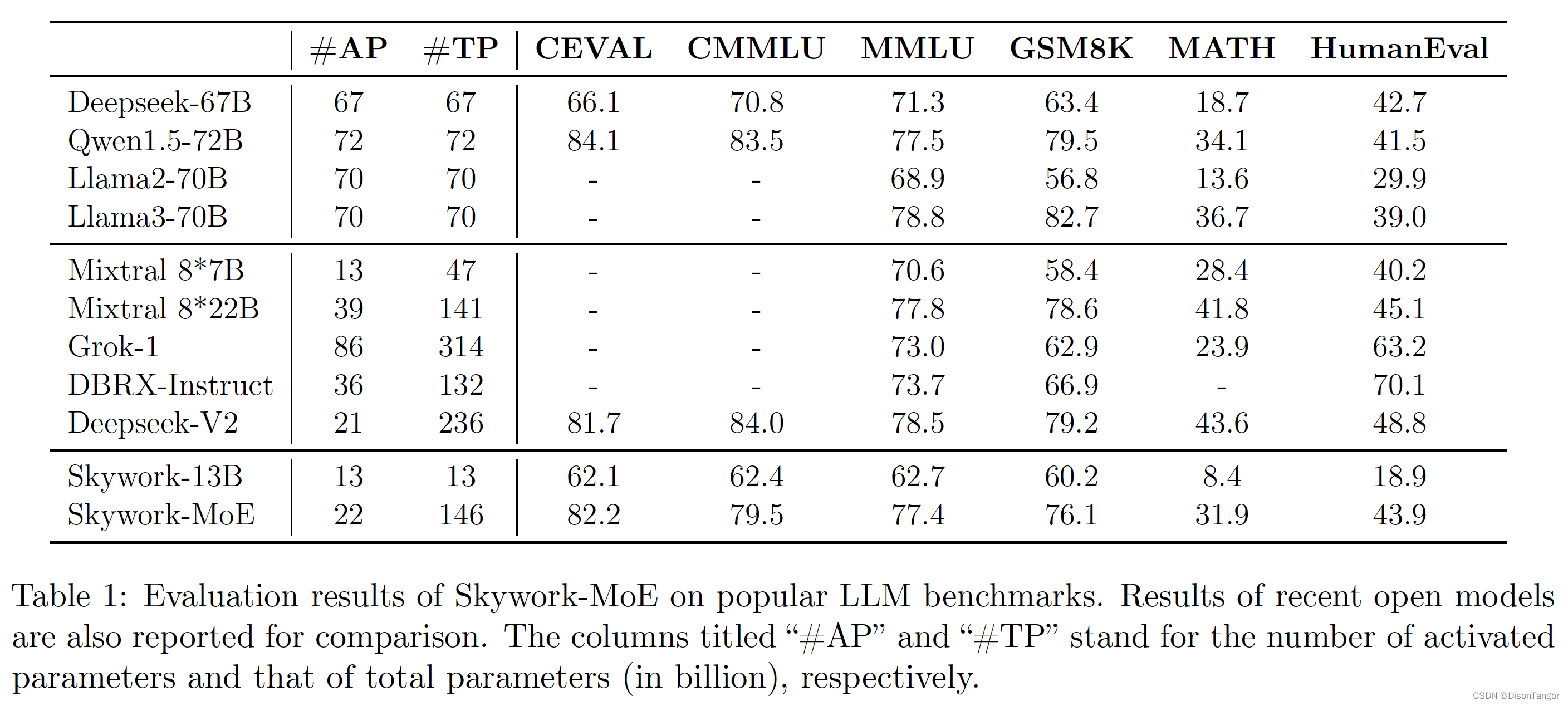
【中国开源生态再添一员】天工AI开源自家的Skywork
刚刚看到《AI高考作文出圈,网友票选天工AI居首》,没想到在Huggingface中发现了Skywork大模型。天工大模型由昆仑万维自研,是国内首个对标ChatGPT的双千亿级大语言模型,天工大模型通过自然语言与用户进行问答式交互,AI生…...
【机器学习300问】109、什么是岭回归模型?
在进行回归任务时间,可以能会遇到特征数量多于观测数量或某些特征变量之间相关性较高(几乎线性相关)时,标准的线性回归模型的系数估计可能非常不精确,可以理解成独立方程个数小于未知数个数此时方程有无穷多解。 例如&…...
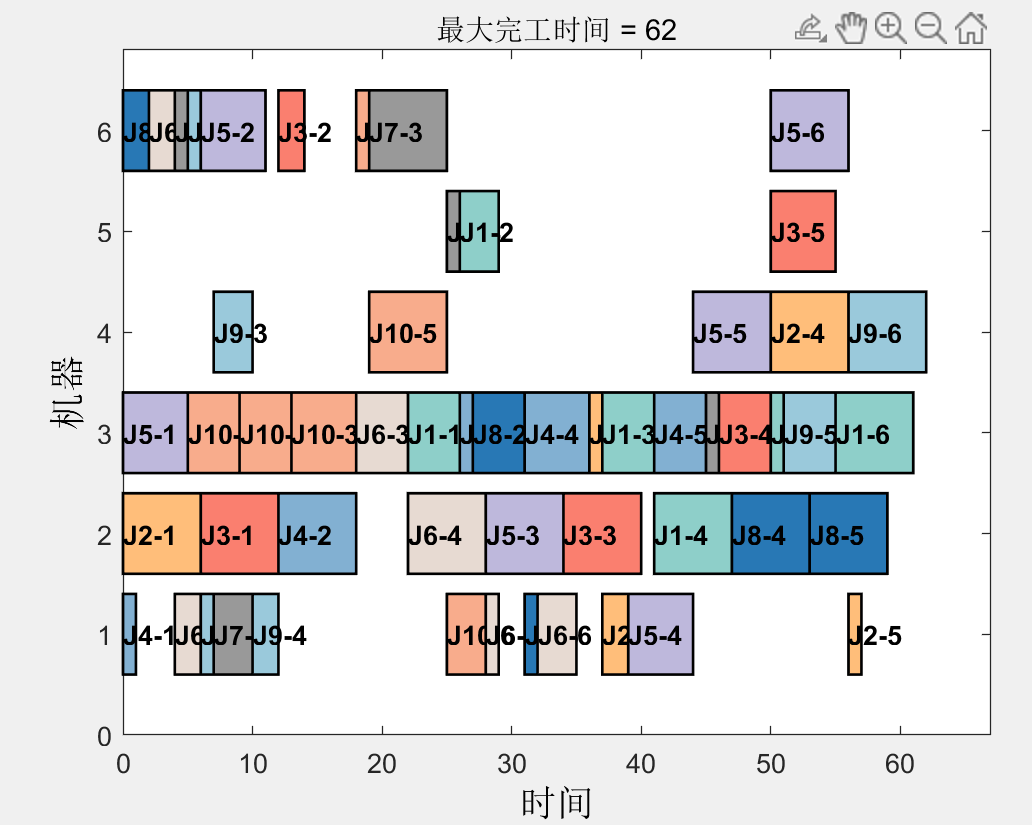
FJSP:烟花算法(FWA)求解柔性作业车间调度问题(FJSP),提供MATLAB代码
一、烟花算法介绍 参考文献: Tan, Y. and Y. Zhu. Fireworks Algorithm for Optimization. in Advances in Swarm Intelligence. 2010. Berlin, Heidelberg: Springer Berlin Heidelberg. 二、烟花算法求解FJSP 2.1FJSP模型介绍 柔性作业车间调度问题(Flexible …...

C++11 列表初始化(initializer_list),pair
1. {} 初始化 C98 中,允许使用 {} 对数组进行初始化。 int arr[3] { 0, 1, 2 };C11 扩大了 {} 初始化 的使用范围,使其可用于所有内置类型和自定义类型。 struct Date {int _year;int _month;int _day;Date(int year, int month, int day):_year(year…...
 和 endswith())
Python3 笔记:字符串的 startswith() 和 endswith()
1、startswith() 方法用于检查字符串是否是以指定子字符串开头,如果是则返回 True,否则返回 False。如果参数 beg 和 end 指定了值,则在指定范围内检查。 语法:str.startswith(substr, beg0,endlen(string)) 参数: s…...

Web前端安全问题分类综合以及XSS、CSRF、SQL注入、DoS/DDoS攻击、会话劫持、点击劫持等详解,增强生产安全意识
前端安全问题是指发生在浏览器、单页面应用、Web页面等前端环境中的各类安全隐患。Web前端作为与用户直接交互的界面,其安全性问题直接关系到用户体验和数据安全。近年来,随着前端技术的快速发展,Web前端安全问题也日益凸显。因此,…...
下列关于脚本的说法不正确的是( )。本题得分: 2分正确答案: A2.单选题 (2分)软件测试自动化的局限性不包含( )。本题得分: 2分)
1.单选题 (2分)下列关于脚本的说法不正确的是( )。本题得分: 2分正确答案: A2.单选题 (2分)软件测试自动化的局限性不包含( )。本题得分: 2分
1.单选题 (2分) 下列关于脚本的说法不正确的是( )。 A 线性脚本是最复杂的脚本 B 结构化脚本具有较好的可读性、可重用性,易于维护 C 关键字驱动脚本在开发时,不关心基础函数,直接使用已定义好的关键字 D 数据驱动脚本将测试脚本和数据进行分离,同一个脚本可以针对不同的输…...

【Docker系列】跨平台 Docker 镜像构建:深入理解`--platform`参数
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

Java-41 深入浅出 Spring - 声明式事务的支持 事务配置 XML模式 XML+注解模式
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
)
Leetcode33( 搜索旋转排序数组)
题目表述 整数数组 nums 按升序排列,数组中的值 互不相同 。 在传递给函数之前,nums 在预先未知的某个下标 k(0 < k < nums.length)上进行了 旋转,使数组变为 [nums[k], nums[k1], …, nums[n-1], nums[0], nu…...

git: early EOF
macOS报错: Initialized empty Git repository in /usr/local/Homebrew/Library/Taps/homebrew/homebrew-core/.git/ remote: Enumerating objects: 2691797, done. remote: Counting objects: 100% (1760/1760), done. remote: Compressing objects: 100% (636/636…...

高考志愿填报管理系统---开发介绍
高考志愿填报管理系统是一款专为教育机构、学校和教师设计的学生信息管理和志愿填报辅助平台。系统基于Django框架开发,采用现代化的Web技术,为教育工作者提供高效、安全、便捷的学生管理解决方案。 ## 📋 系统概述 ### 🎯 系统定…...

一些实用的chrome扩展0x01
简介 浏览器扩展程序有助于自动化任务、查找隐藏的漏洞、隐藏自身痕迹。以下列出了一些必备扩展程序,无论是测试应用程序、搜寻漏洞还是收集情报,它们都能提升工作流程。 FoxyProxy 代理管理工具,此扩展简化了使用代理(如 Burp…...
Element-Plus:popconfirm与tooltip一起使用不生效?
你们好,我是金金金。 场景 我正在使用Element-plus组件库当中的el-popconfirm和el-tooltip,产品要求是两个需要结合一起使用,也就是鼠标悬浮上去有提示文字,并且点击之后需要出现气泡确认框 代码 <el-popconfirm title"是…...

从0开始学习R语言--Day17--Cox回归
Cox回归 在用医疗数据作分析时,最常见的是去预测某类病的患者的死亡率或预测他们的结局。但是我们得到的病人数据,往往会有很多的协变量,即使我们通过计算来减少指标对结果的影响,我们的数据中依然会有很多的协变量,且…...
