【机器学习300问】109、什么是岭回归模型?
在进行回归任务时间,可以能会遇到特征数量多于观测数量或某些特征变量之间相关性较高(几乎线性相关)时,标准的线性回归模型的系数估计可能非常不精确,可以理解成独立方程个数小于未知数个数此时方程有无穷多解。
例如:1个方程,2个未知数时,此时方程数量小于未知数个数,有无穷多解。
| 序号 | 方程组的解 |
| 解1 | |
| 解2 | |
| ... | |
| 解m | |
| 独立方程数量小于未知数个数,方程组有无穷多解 | |
一、岭回归产生的背景
岭回归模型的提出为了解决什么问题呢?我们用一个比喻加一个例子来说明:
想象一下,你在一家咖啡馆里试图通过窗户观察外面行人手中的饮料类型来进行统计。但是,由于窗户上贴满了复杂的花纹,这些花纹就像是数据中的噪音和复杂关系,让你很难清晰地分辨每种饮料。这时候,如果你戴上一副特制的眼镜——这副眼镜能减弱花纹干扰,让你更专注于主要的区别特征,比如饮料的颜色或形状,这样就能更准确地统计了。
在机器学习中,岭回归就是这样一副“眼镜”。它是一种改进的线性回归方法,专门用来处理那些因为特征之间存在很强的相关性(我们称之为多重共线性)而变得棘手的问题。没有这副“眼镜”,普通的线性回归(就像直接用眼观察)可能会被数据中的复杂关系迷惑,导致预测效果很差,甚至系数估计出错。
二、岭回归的思想和公式
岭回归是如何工作的呢?它通过在原有的误差最小化目标基础上,加入了一个额外的惩罚项。这个惩罚项是各个特征权重(也就是回归系数)的平方和乘以一个正的常数(我们称之为正则化参数λ)。
在标准的多元线性回归中,模型参数通过最小化残差平方和(RSS)来估计:
其中,是样本数量,
是因变量的观测值,
是自变量的观测值,
是回归系数。
然而,在某些情况下,特别是当特征数量接近或超过样本数量时,线性回归可能导致过拟合和不稳定的估计值。岭回归为了防止这些问题,将一个额外的正则项(也称为惩罚项)加到RSS上:
其中,是一个正的调节参数(岭参数),起到调节系数向0收缩的力度。由于正则项的存在,岭回归倾向于将系数估计值向0压缩,这意味着尽管它们可能永远不会等于0,但可以控制过拟合现象,提高模型的泛化能力。
【注】选择一个合适的值,因为它决定了系数压缩的程度。
的值越大,约束越强,回归系数会越小。通常
是通过交叉验证来选择的。
三、为什么叫岭回归?
岭回归之所以被称为“岭回归”(Ridge Regression),源自它在问题求解中的几何性质。这个名字可以归因于它在求解参数时,通过正则化项引入的约束导致解集呈现出“岭”的形状。
在标准线性回归中,模型的目标是最小化误差平方和,这在参数空间中可以视为寻找一个能使误差平方和函数最低的参数点。如果存在共线性,这个误差平方和的底部(代表最佳解的区域)会变得非常扁平,导致许多可能的解。
当引入岭回归的L2正则化时,即在目标函数中增加所有系数的平方和乘以岭参数λ,这就相当于在参数空间中增加了一个圆形的约束。这个圆形约束使得参数不再在平坦的区域自由移动,而是被限制在一个“岭”上,即限制在较小范围的圆形区域内寻找最佳解。因此,“岭”这个名称形象地描述了正则化项如何影响系数的求解过程,强制系数向零收缩,同时保护模型免于过拟合。
关于岭回归的代码演示:
学习岭回归![]() https://gitee.com/wx114/linear-ridge-lasso-regression.git
https://gitee.com/wx114/linear-ridge-lasso-regression.git
相关文章:
【机器学习300问】109、什么是岭回归模型?
在进行回归任务时间,可以能会遇到特征数量多于观测数量或某些特征变量之间相关性较高(几乎线性相关)时,标准的线性回归模型的系数估计可能非常不精确,可以理解成独立方程个数小于未知数个数此时方程有无穷多解。 例如&…...
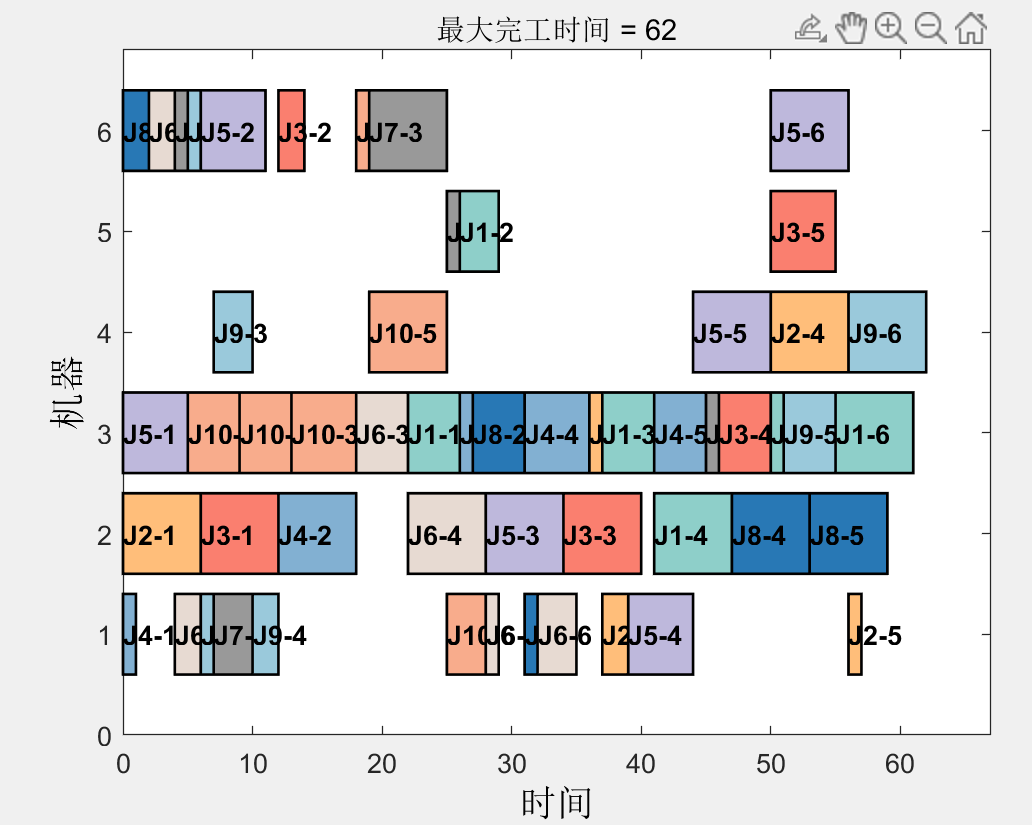
FJSP:烟花算法(FWA)求解柔性作业车间调度问题(FJSP),提供MATLAB代码
一、烟花算法介绍 参考文献: Tan, Y. and Y. Zhu. Fireworks Algorithm for Optimization. in Advances in Swarm Intelligence. 2010. Berlin, Heidelberg: Springer Berlin Heidelberg. 二、烟花算法求解FJSP 2.1FJSP模型介绍 柔性作业车间调度问题(Flexible …...

C++11 列表初始化(initializer_list),pair
1. {} 初始化 C98 中,允许使用 {} 对数组进行初始化。 int arr[3] { 0, 1, 2 };C11 扩大了 {} 初始化 的使用范围,使其可用于所有内置类型和自定义类型。 struct Date {int _year;int _month;int _day;Date(int year, int month, int day):_year(year…...
 和 endswith())
Python3 笔记:字符串的 startswith() 和 endswith()
1、startswith() 方法用于检查字符串是否是以指定子字符串开头,如果是则返回 True,否则返回 False。如果参数 beg 和 end 指定了值,则在指定范围内检查。 语法:str.startswith(substr, beg0,endlen(string)) 参数: s…...

Web前端安全问题分类综合以及XSS、CSRF、SQL注入、DoS/DDoS攻击、会话劫持、点击劫持等详解,增强生产安全意识
前端安全问题是指发生在浏览器、单页面应用、Web页面等前端环境中的各类安全隐患。Web前端作为与用户直接交互的界面,其安全性问题直接关系到用户体验和数据安全。近年来,随着前端技术的快速发展,Web前端安全问题也日益凸显。因此,…...
下列关于脚本的说法不正确的是( )。本题得分: 2分正确答案: A2.单选题 (2分)软件测试自动化的局限性不包含( )。本题得分: 2分)
1.单选题 (2分)下列关于脚本的说法不正确的是( )。本题得分: 2分正确答案: A2.单选题 (2分)软件测试自动化的局限性不包含( )。本题得分: 2分
1.单选题 (2分) 下列关于脚本的说法不正确的是( )。 A 线性脚本是最复杂的脚本 B 结构化脚本具有较好的可读性、可重用性,易于维护 C 关键字驱动脚本在开发时,不关心基础函数,直接使用已定义好的关键字 D 数据驱动脚本将测试脚本和数据进行分离,同一个脚本可以针对不同的输…...

【Docker系列】跨平台 Docker 镜像构建:深入理解`--platform`参数
💝💝💝欢迎来到我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:kwan 的首页,持续学…...

力扣1248.统计优美子数组
力扣1248.统计优美子数组 同930. 哈希表法 求前缀和 class Solution {public:int numberOfSubarrays(vector<int>& nums, int k) {int n nums.size();unordered_map<int,int> cnt;int res0,sum0;for(int i0,j0;i<n;i){cnt[sum] ;if(nums[i] & 1) …...

AI2THOR 2.1.0使用教程
一、安装和入门 1.1 AI2-THOR使用要求 操作系统: Mac OS X 10.9, Ubuntu 14.04显卡:DX9(着色器型号 3.0)或 DX11,功能级别为 9.3。CPU:支持 SSE2 指令集。Python 2.7 或 Python 3.5Linux 用户…...

在Nginx中配置php程序环境。
1、前言。 我一开始是想 搭建 Tomcat PHP 环境。 Tomcat并不能直接运行PHP,因为Tomcat是一个Java Web服务器,主要用于运行Java应用程序。但是,我们可以通过一些配置和工具来使Tomcat能够运行PHP。 在配置Tomcat支持PHP 项目的时…...

!力扣70. 爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢? 1. 递归(超时) class Solution { public:int climbStairs(int n) {if(n1){return 1;}if(n2){return 2;}return climbStairs…...
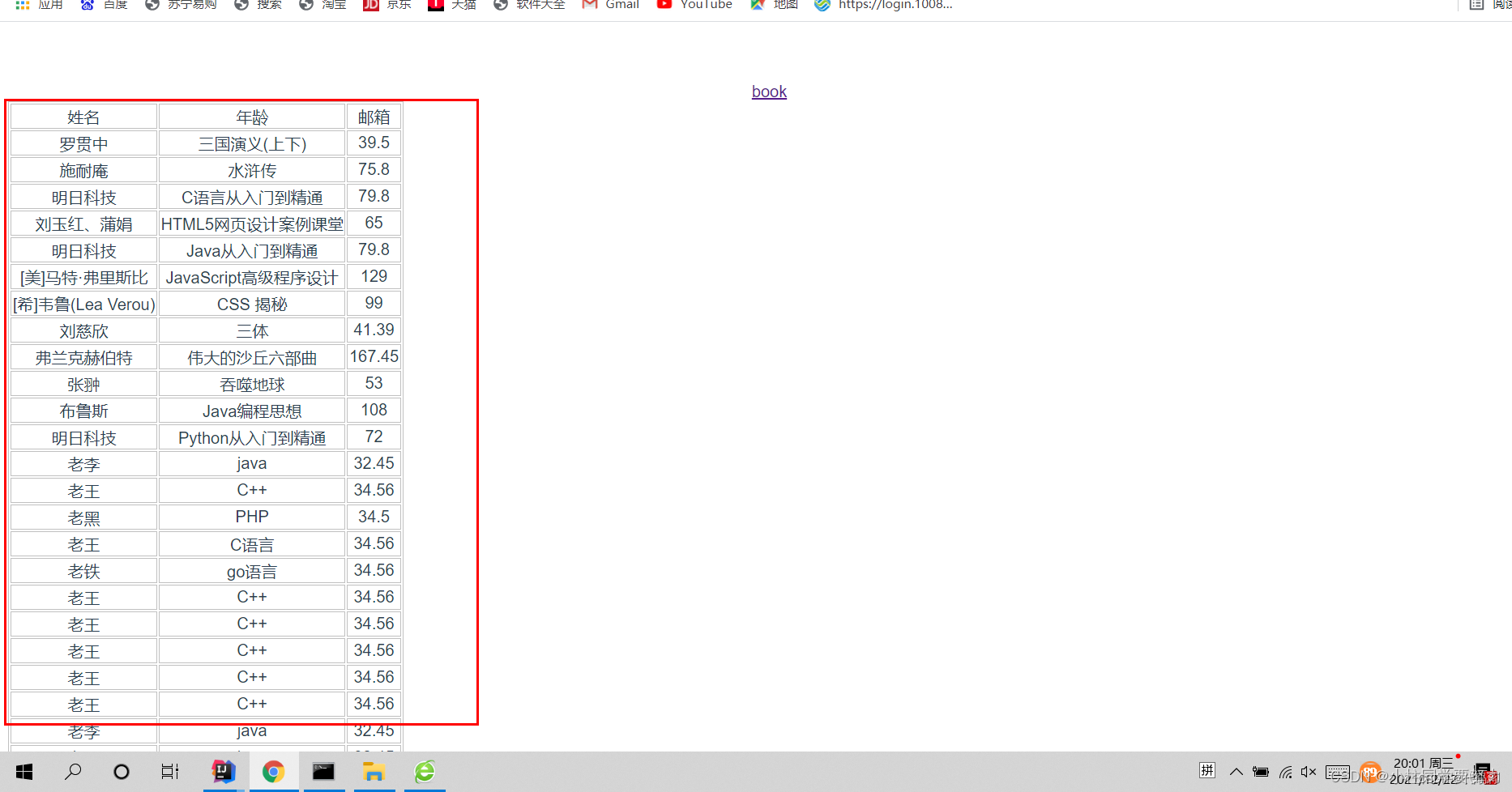
Spring boot+vue前后端分离
目录 1、前端vue的搭建 2、后端项目的构建 pom文件中引入的jar包 yml文件用来配置连接数据库和端口的设置 application.property进行一些整合 service层 imp层 mapper 实体类 额外写一个类、解决跨域问题 3、测试 1、前端vue的搭建 建立项目的过程略 开启一个建立好…...

Python基础总结之列表转字符串
Python基础总结之列表转字符串 在Python中,将列表转换为字符串有多种方法,最常用的是使用str.join()方法。这里有一些示例: 使用str.join()方法 这是将列表转换为字符串的最直接和最常用的方法。你需要确保列表中的所有元素都是字符串类型…...

二分【1】二分查找框架 查找指定元素
目录 二分查找 基本思想 几种情况汇总 一。严格递增序列 1.查找本身 2.查找第一个大于等于自己的 3.查找第一个大于自己的 4.严格递减序列 二。有重复元素 1.取其中第一个出现的 2.取其中最后一个出现的 二分查找 基本思想 几种情况汇总 一。严格递增序列 1.查找本身…...

Python 中如何使用 lambda 函数
在 Python 中,可以使用 lambda 函数来创建匿名函数。lambda 函数的语法是:lambda 参数: 表达式。以下是一些使用 lambda 函数的例子: 通过 lambda 函数来计算两个数的和: add lambda x, y: x y print(add(2, 3)) # 输出 5通过…...
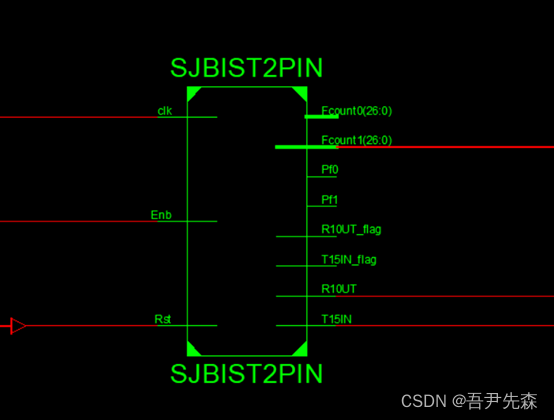
关于焊点检测(SJ-BIST)模块实现
关于焊点检测(SJ-BIST)模块实现 语言 :Verilg HDL 、VHDL EDA工具:ISE、Vivado、Quartus II 关于焊点检测(SJ-BIST)模块实现一、引言二、焊点检测功能的实现方法(1) 输入接口&#x…...

关于修改Python中pip默认安装路径的终极方法
别想了,终极方法就是手动复制,不过我可以给你参考一下手动复制的方法 关于手动移动pip安装包的方法 别想了,终极方法就是手动复制,不过我可以给你参考一下手动复制的方法一、首先确认一下pip默认安装路径二、再确认一下需要移动到…...
android集成百度文心一言实现对话功能,实战项目讲解,人人都能拥有一款ai应用
大家好,今天给大家讲解下如何实现一个基于百度文心一言的app功能,app内部同时集成了讯飞的语音识别。本文适用于有android基础的小伙伴阅读,文章末尾放上本项目用到的全部实例代码,在使用前请务必看完本文章。 先来给大家看看效果…...

事件总线vueEvent
一个组件结束后要更新另一个组件数据,但是另一个组件和这个组件没有上下级关系 在 Vue 中,非父子组件之间进行通信通常需要使用事件总线或者其他的全局事件管理器。vueEvent 似乎是一个事件总线对象,通过 emit 方法触发了名为 updateData 的事…...

设计模式之观察者模式ObserverPattern(十一)
一、概述 观察者模式 (Observer Pattern) 是一种行为型设计模式,又被称为发布-订阅 (Publish/Subscribe) 模式,它定义了对象之间的一种一对多的依赖关系,使得当一个对象的状态发生变化时,所有依赖于它的对象都会自动收到通知并更新…...

网络六边形受到攻击
大家读完觉得有帮助记得关注和点赞!!! 抽象 现代智能交通系统 (ITS) 的一个关键要求是能够以安全、可靠和匿名的方式从互联车辆和移动设备收集地理参考数据。Nexagon 协议建立在 IETF 定位器/ID 分离协议 (…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

QT3D学习笔记——圆台、圆锥
类名作用Qt3DWindow3D渲染窗口容器QEntity场景中的实体(对象或容器)QCamera控制观察视角QPointLight点光源QConeMesh圆锥几何网格QTransform控制实体的位置/旋转/缩放QPhongMaterialPhong光照材质(定义颜色、反光等)QFirstPersonC…...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

k8s从入门到放弃之HPA控制器
k8s从入门到放弃之HPA控制器 Kubernetes中的Horizontal Pod Autoscaler (HPA)控制器是一种用于自动扩展部署、副本集或复制控制器中Pod数量的机制。它可以根据观察到的CPU利用率(或其他自定义指标)来调整这些对象的规模,从而帮助应用程序在负…...

全面解析数据库:从基础概念到前沿应用
在数字化时代,数据已成为企业和社会发展的核心资产,而数据库作为存储、管理和处理数据的关键工具,在各个领域发挥着举足轻重的作用。从电商平台的商品信息管理,到社交网络的用户数据存储,再到金融行业的交易记录处理&a…...
