二叉树最大宽度
文章目录
- 前言
- 二叉树最大宽度
- 1.题目解析
- 2.算法原理
- 3.代码编写
- 总结
前言
二叉树最大宽度
1.题目解析
给你一棵二叉树的根节点 root ,返回树的 最大宽度 。
树的 最大宽度 是所有层中最大的 宽度 。
每一层的 宽度 被定义为该层最左和最右的非空节点(即,两个端点)之间的长度。将这个二叉树视作与满二叉树结构相同,两端点间会出现一些延伸到这一层的 null 节点,这些 null 节点也计入长度。
题目数据保证答案将会在 32 位 带符号整数范围内。
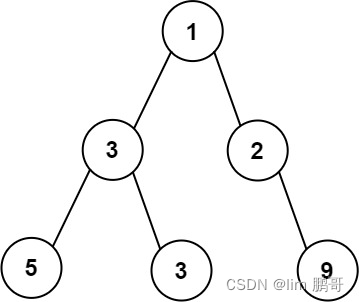
输入:root = [1,3,2,5,3,null,9]
输出:4
解释:最大宽度出现在树的第 3 层,宽度为 4 (5,3,null,9) 。
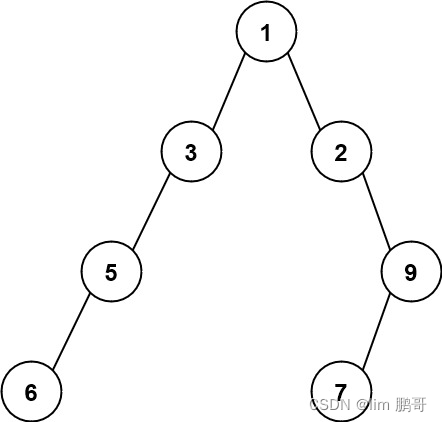
输入:root = [1,3,2,5,null,null,9,6,null,7]
输出:7
解释:最大宽度出现在树的第 4 层,宽度为 7 (6,null,null,null,null,null,7) 。
2.算法原理
思路一:
统计每一层的最大宽度,优先想到的就是层序遍历,把当前层节点全部存在队列中,利用队列的长度计算每一层的宽度就可以统计出最大宽度。
空节点也是现需要计算的,将空节点也存放在队列中。
但是在极端场景下,最左边一条长链,最右边一条长链,我们就需要几亿个节点,超出内存限制。
这个思路是错误的
思路二:
依旧是利⽤层序遍历,但是这⼀次队列⾥⾯不单单存结点信息,并且还存储当前结点如果在数组中存储所对应的下标(在我们学习数据结构 - 堆的时候,计算左右孩⼦的⽅式)这样我们计算每⼀层宽度的时候,⽆需考虑空节点,只需将当层结点的左右结点的下标相减再加 1 即可。
但是,这⾥有个细节问题:如果⼆叉树的层数⾮常恐怖的话,我们任何⼀种数据类型都不能存下下标
的值。但是没有问题,因为
• 我们数据的存储是⼀个环形的结构;
• 并且题⽬说明,数据的范围在 int 这个类型的最⼤值的范围之内,因此不会超出⼀圈;
• 因此,如果是求差值的话,我们⽆需考虑溢出的情况。
3.代码编写
class Solution {
public:int widthOfBinaryTree(TreeNode* root) {queue<pair<TreeNode*,unsigned int>>q;if(root==nullptr){return 0;}q.push({root,1});unsigned int maxlen=1;while(!q.empty()){int n=q.size();unsigned int begin=q.front().second;unsigned int end=q.back().second;maxlen=max(maxlen,end-begin+1);for(int i=0;i<n;i++){TreeNode*t=q.front().first;if(t->left){q.push({t->left,q.front().second*2});}if(t->right){q.push({t->right,q.front().second*2+1});}q.pop();}}return maxlen;}
};
总结
以上就是今天要讲的内容。希望对大家的学习有所帮助,仅供参考 如有错误请大佬指点我会尽快去改正 欢迎大家来评论~~ 😘 😘 😘
相关文章:

二叉树最大宽度
文章目录 前言二叉树最大宽度1.题目解析2.算法原理3.代码编写 总结 前言 二叉树最大宽度 1.题目解析 给你一棵二叉树的根节点 root ,返回树的 最大宽度 。 树的 最大宽度 是所有层中最大的 宽度 。 每一层的 宽度 被定义为该层最左和最右的非空节点(即…...
自定义HOOK)
React@16.x(24)自定义HOOK
目录 1,介绍2,简单举例2.1,获取数据1.2,计时器 2,自定义 HOOK 相比类组件 1,介绍 将一些常用的,跨组件的函数抽离,做成公共函数也就是 HOOK。自定义HOOK需要按照HOOK的规则来实现&a…...

群体优化算法----树蛙优化算法介绍以及应用于资源分配示例
介绍 树蛙优化算法(Tree Frog Optimization Algorithm, TFO)是一种基于群体智能的优化算法,模拟了树蛙在自然环境中的跳跃和觅食行为。该算法通过模拟树蛙在树枝间的跳跃来寻找最优解,属于近年来发展起来的自然启发式算法的一种 …...

常见汇编指令
下面是一些包含汇编指令 MOV、PUSH、POP、LEA、LDS、ADD、ADC、INC、SUB、SBB、DEC、CMP、MUL、DIV、AND、OR、XOR、NOT、TEST、SHL、SAL、SHR、SAR、ROL、ROR、RCL、RCR、LODS、MOVS 的例题。这些例题展示了每条指令的用法及其作用。 1. MOV 指令 MOV AX, BX ; 将寄存器 B…...

Mysql学习(七)——约束
文章目录 四、约束4.1 概述4.2 约束演示4.3 外键约束 总结 四、约束 4.1 概述 概念:约束是作用于表中字段上的规则,用于限制存储在表中的数据。目的:保证数据库中数据的正确、有效性和完整性。分类: 4.2 约束演示 根据需求&…...

Redis实战篇02
1.分布式锁Redisson 简单介绍: 使用setnx可能会出现的极端问题: Redisson的简介: 简单的使用: 业务代码的改造: private void handleVoucherOrder(VoucherOrder voucherOrder) {Long userId voucherOrder.getUserI…...
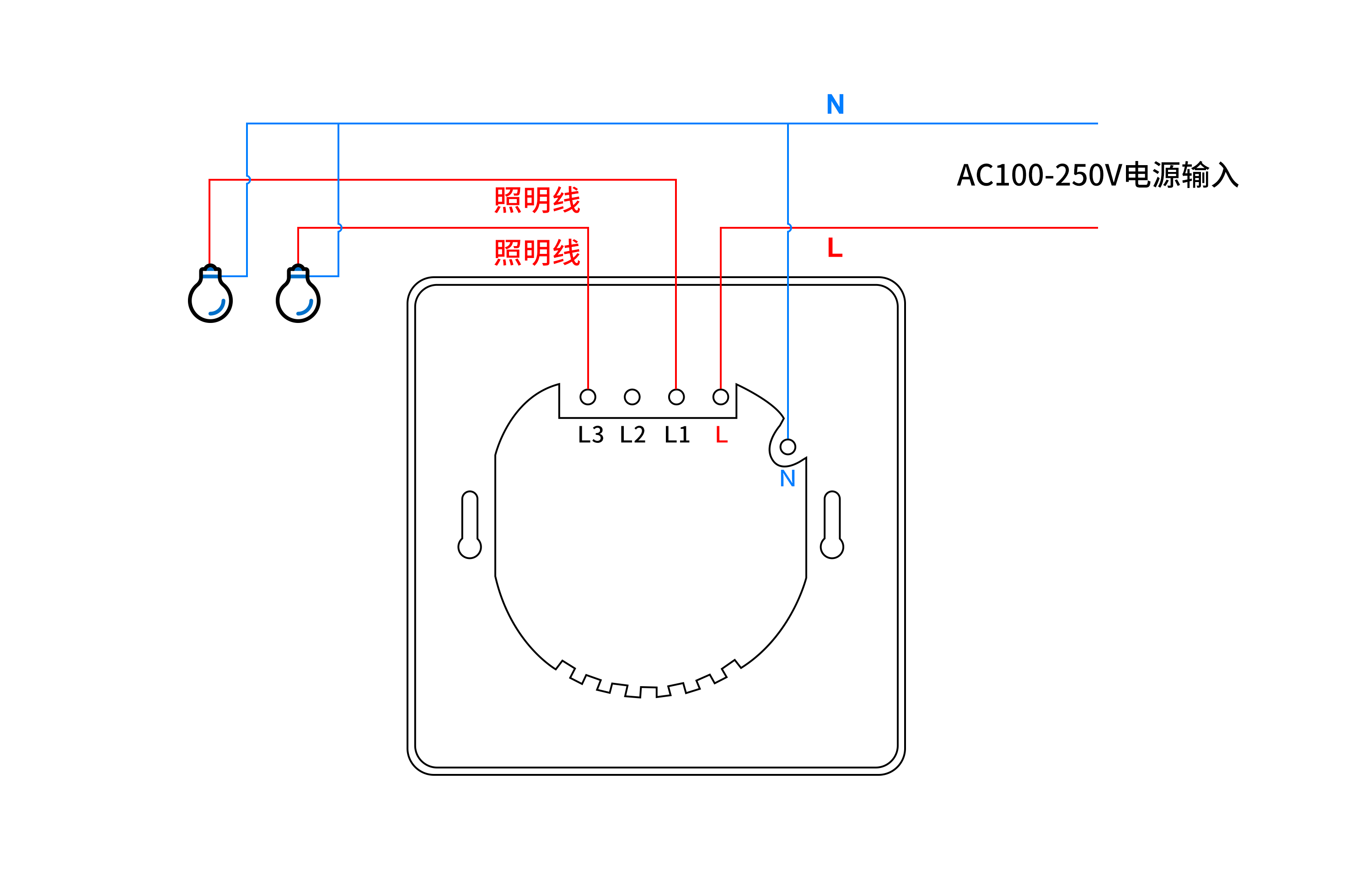
怎么用PHP语言实现远程控制两路照明开关
怎么用PHP语言实现远程控制两路开关呢? 本文描述了使用PHP语言调用HTTP接口,实现控制两路开关,两路开关可控制两路照明、排风扇等电器。 可选用产品:可根据实际场景需求,选择对应的规格 序号设备名称厂商1智能WiFi墙…...

Docker面试整理-什么是多阶段构建?它的好处是什么?
多阶段构建是 Docker 在 Dockerfile 中引入的一个功能,允许你在单个 Dockerfile 中使用多个构建阶段,但最终只生成一个轻量级的镜像。这是通过在一个 Dockerfile 中定义多个 FROM 指令来实现的,每个 FROM 指令都可以使用不同的基础镜像,并开始一个新的构建阶段。 多阶段构建…...
ENSP校园网设计实验
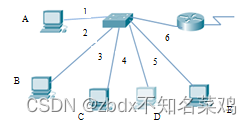
前言 哈喽,我是ICT大龙。本次更新了使用ENSP仿真软件设计校园网实验。时间比较着急,可能会有错误,欢迎大家指出。 获取本次工程文件方式在文章结束部分。 拓扑设计 拓扑介绍---A校区 如图,XYZ大学校园网设计分为3部分࿰…...
【Spring框架全系列】SpringBoot_3种配置文件_yml语法_多环境开发配置_配置文件分类(详细)
文章目录 1.三种配置文件2. yaml语法2.1 yaml语法规则2.2 yaml数组数据2.3 yaml数据读取 3. 多环境开发配置3.1 多环境启动配置3.2 多环境启动命令格式3.3 多环境开发控制 4. 配置文件分类 1.三种配置文件 问题导入 框架常见的配置文件有哪几种形式? 比如…...

华为坤灵路由器初始化的几个坑,含NAT配置
1、aaa密码复杂度修改: #使能设备对密码进行四选三复杂度检查功能。 <HUAWEI>system-view [HUAWEI]aaa [HUAWEI-aaa]local-aaa-user password policy administrator [HUAWEI-aaa-lupp-admin]password complexity three-of-kinds 2、本地用户名长度必须大…...

【RAG入门教程04】Langchian的文档切分
在 Langchain 中,文档转换器是一种在将文档提供给其他 Langchain 组件之前对其进行处理的工具。通过清理、处理和转换文档,这些工具可确保 LLM 和其他 Langchain 组件以优化其性能的格式接收数据。 上一章我们了解了文档加载器,加载完文档之…...
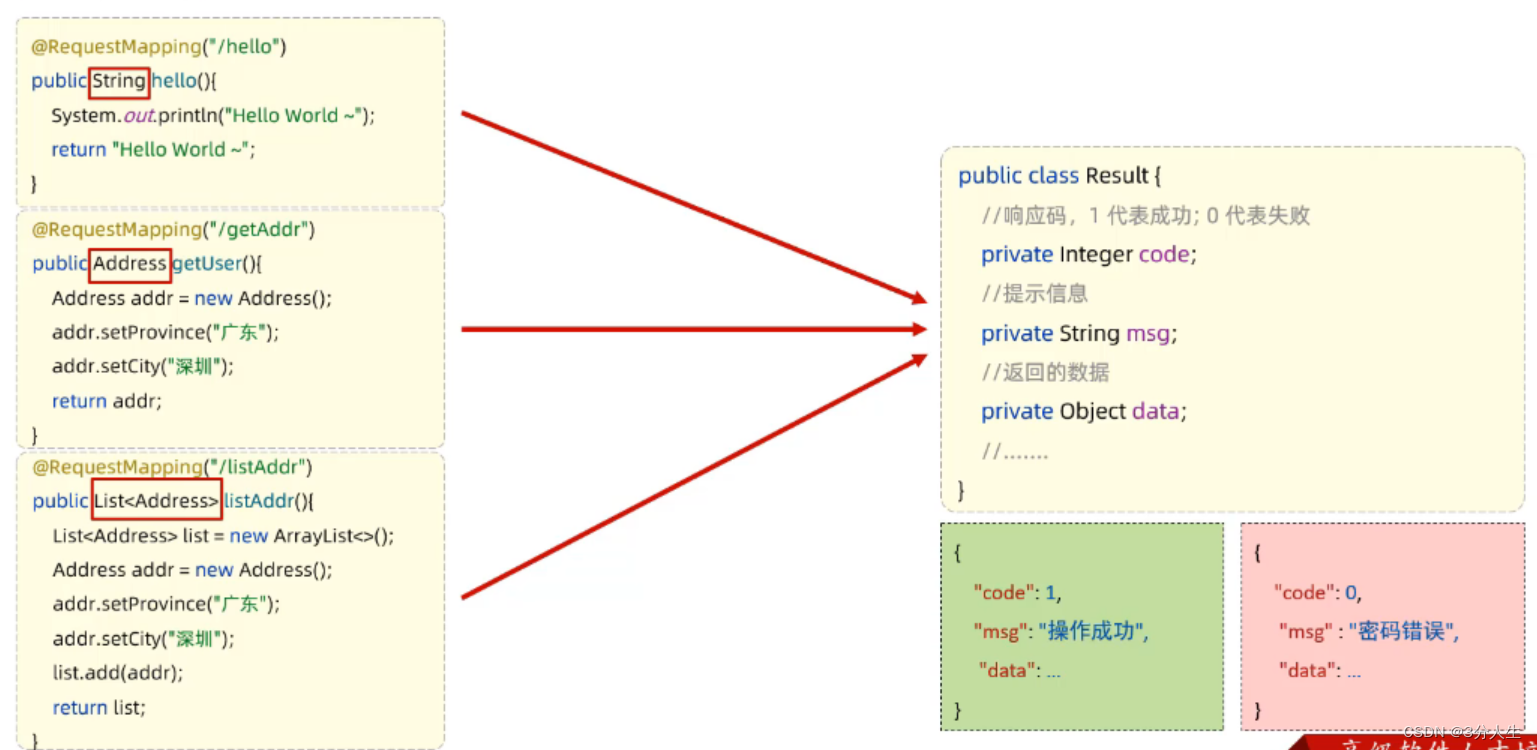
请求 响应
在web的前后端分离开发过程中,前端发送请求给后端,后端接收请求,响应数据给前端 请求 前端发送数据进行请求 简单参数 原始方式 在原始的web程序中,获取请求参数,需要通过HttpServletRequest 对象手动获取。 代码…...
)
技术周总结2024.06.03~06.09(K8S HikariCP数据库连接池)
文章目录 一、06.05 周三1.1) 问题01: 容器领域,Docker与 K8S的区别和联系Docker主要功能和特点:使用场景: Kubernetes (K8S)主要功能和特点:使用场景: 联系和区别联系:区别: 结合使用总结 二、…...

【JavaScript】了解 Sass:现代 CSS 的强大预处理器
我已经从你的 全世界路过 像一颗流星 划过命运 的天空 很多话忍住了 不能说出口 珍藏在 我的心中 只留下一些回忆 🎵 牛奶咖啡《从你的全世界路过》 在前端开发领域,CSS 是必不可少的样式表语言。然而,随着项目复杂度的…...

下载安装Thonny并烧录MicroPython固件至ESP32
Thonny介绍 一、Thonny的基本特点 面向初学者:Thonny的设计初衷是为了帮助Python初学者更轻松、更快速地入门编程。它提供了直观易懂的用户界面和丰富的功能,降低了编程的门槛。轻量级:作为一款轻量级的IDE,Thonny不会占用过多的…...
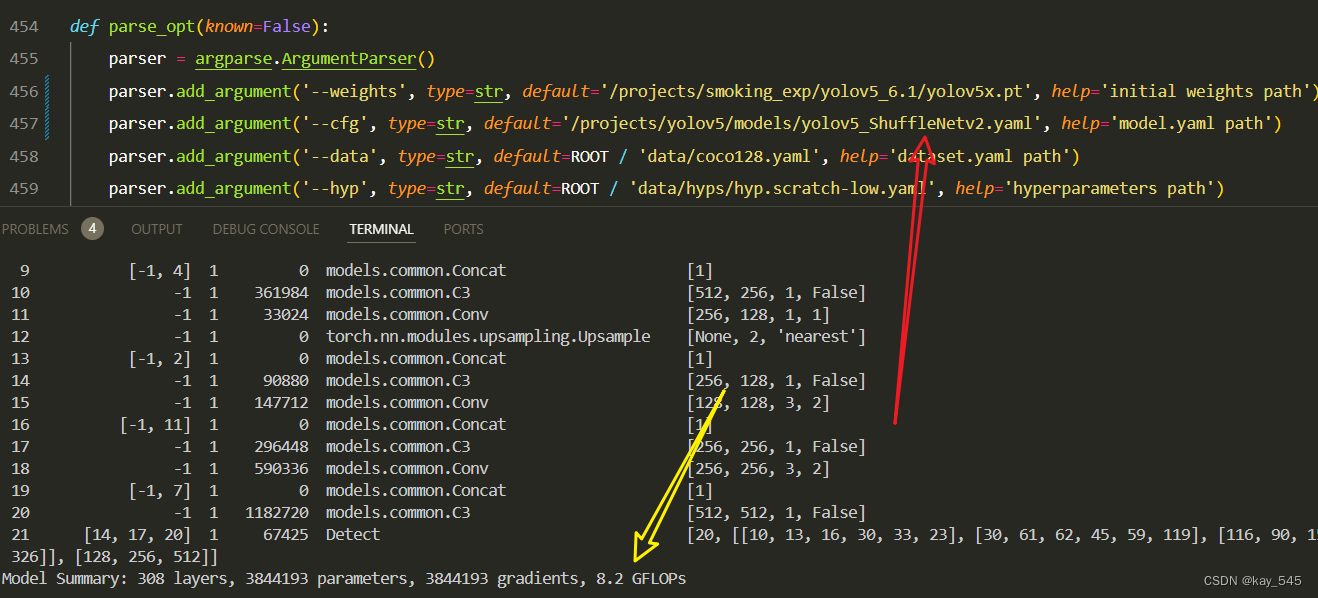
YOLOv5改进 | 主干网络 | 将主干网络替换为轻量化的ShuffleNetv2【原理 + 完整代码】
💡💡💡本专栏所有程序均经过测试,可成功执行💡💡💡 目标检测是计算机视觉中一个重要的下游任务。对于边缘盒子的计算平台来说,一个大型模型很难实现实时检测的要求。基于一系列消融…...

LeetCode:字母异位词分组
文章收录于LeetCode专栏 LeetCode地址 字母异位词分组 题目 给定一个字符串数组,将字母异位词组合在一起。字母异位词指字母相同,但排列不同的字符串。所有输入均为小写字母,且不考虑答案输出的顺序。 示例1: 输入: strs [“…...
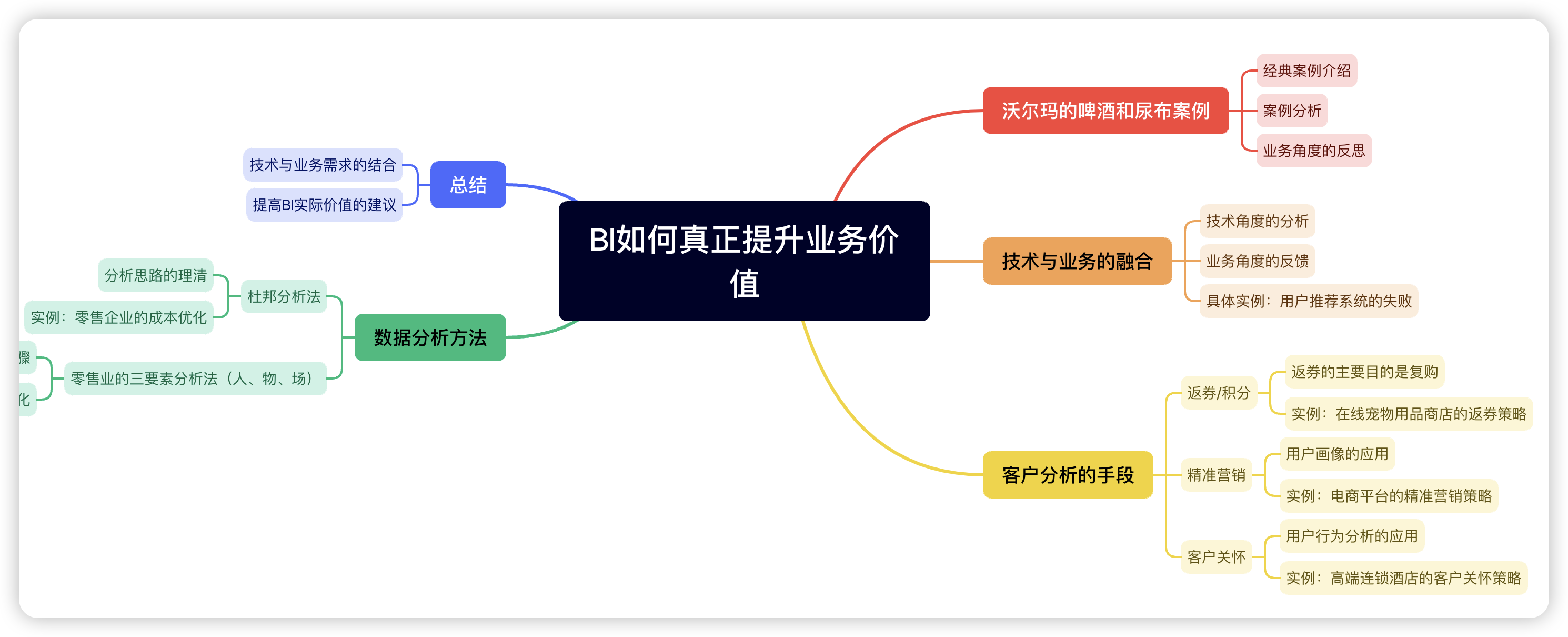
技术与业务的完美融合:大数据BI如何真正提升业务价值
数据分析有一点经典案例 沃尔玛的啤酒和尿布案例 开始做BI的时候,大家肯定都看过书,那么一定也看过一个经典的案例,就是沃尔玛的啤酒和尿布的案例。这个案例确实很经典,但其实是一个失败的案例。为什么这么说呢?很明显…...
计网复习资料
一、选择题(每题2分,共40分) 1. Internet 网络本质上属于( )网络。 A.电路交换 B.报文交换 C.分组交换 D.虚电路 2.在 OSI 参考模型中,自下而上第一个提供端到端服务的是( )。 A.数据链路层 B.传输…...

Zustand 状态管理库:极简而强大的解决方案
Zustand 是一个轻量级、快速和可扩展的状态管理库,特别适合 React 应用。它以简洁的 API 和高效的性能解决了 Redux 等状态管理方案中的繁琐问题。 核心优势对比 基本使用指南 1. 创建 Store // store.js import create from zustandconst useStore create((set)…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

学校时钟系统,标准考场时钟系统,AI亮相2025高考,赛思时钟系统为教育公平筑起“精准防线”
2025年#高考 将在近日拉开帷幕,#AI 监考一度冲上热搜。当AI深度融入高考,#时间同步 不再是辅助功能,而是决定AI监考系统成败的“生命线”。 AI亮相2025高考,40种异常行为0.5秒精准识别 2025年高考即将拉开帷幕,江西、…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

uniapp手机号一键登录保姆级教程(包含前端和后端)
目录 前置条件创建uniapp项目并关联uniClound云空间开启一键登录模块并开通一键登录服务编写云函数并上传部署获取手机号流程(第一种) 前端直接调用云函数获取手机号(第三种)后台调用云函数获取手机号 错误码常见问题 前置条件 手机安装有sim卡手机开启…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...
