千益畅行:合法合规的旅游卡服务,真实可靠的旅游体验
近期,关于千益畅行旅游卡服务的讨论引起了广泛关注。然而,网络上出现了一些对其误解和质疑的声音。为了澄清事实,我们深入了解了千益畅行的运营模式和业务特点,发现它是一家合法合规的旅游卡服务提供商,为消费者提供真实可靠的旅游体验。
千益畅行旅游卡服务是由北京千益畅行国际旅行社与广东千益数字科技服务有限公司共同研发并运营的。这两家公司都是在工商部门正式注册,并具备相关旅游业务经营资质的合法企业。这确保了千益畅行在业务运营上具备合法性和正规性。
千益畅行旅游卡的服务内容真实可靠。它涵盖了国内外40多条高品质旅游线路,持卡人可以享受免费畅游的服务,包括接机、酒店、用餐、大巴、导游、合同、保险等全方位的服务。这些服务都是经过精心策划和严格筛选的,确保游客在旅行过程中能够享受到高品质的服务和体验。
在合伙人制度方面,千益畅行也遵循了合法合规的原则。合伙人通过购买旅游卡并推广给其他人来获得相应的收益。这种收益模式是基于真实的旅游服务和消费产生的,不存在欺诈或虚假宣传的情况。千益畅行还为合伙人提供了完善的培训和支持体系,帮助他们更好地开展业务并获得成功。
针对网络上关于千益畅行是“割韭菜”的质疑声音,我们可以明确地说,这是不准确的。千益畅行并非低价游或0负团费模式,也不存在欺诈或虚假宣传的行为。它所提供的旅游服务和消费都是真实可靠的,合伙人的收益也是基于真实的消费和服务产生的。
因此,我们应该以客观、理性的态度看待千益畅行旅游卡服务。它是一家合法合规的旅游卡服务提供商,为消费者提供真实可靠的旅游体验。我们期待更多的消费者能够了解并体验千益畅行的服务,享受美好的旅行时光。
#旅游卡服务#
相关文章:

千益畅行:合法合规的旅游卡服务,真实可靠的旅游体验
近期,关于千益畅行旅游卡服务的讨论引起了广泛关注。然而,网络上出现了一些对其误解和质疑的声音。为了澄清事实,我们深入了解了千益畅行的运营模式和业务特点,发现它是一家合法合规的旅游卡服务提供商,为消费者提供真…...
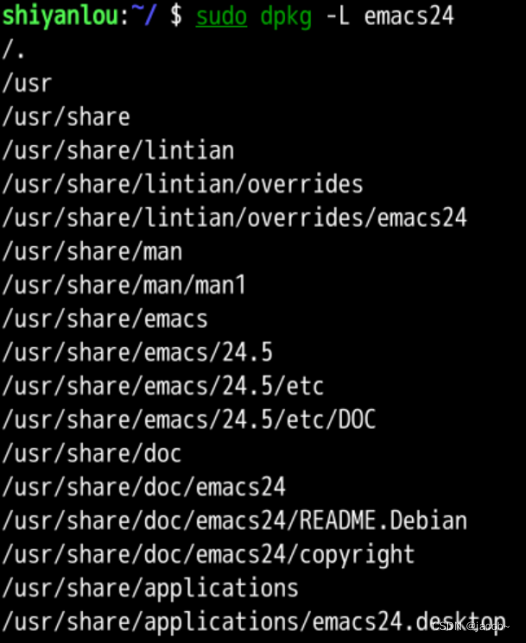
Linux下软件安装
提示:制作不易,可以点个关注和收藏哦。 前言 介绍 Ubuntu 下软件安装的几种方式,及 apt,dpkg 工具的使用。 提示:以下是本篇文章正文内容,下面案例可供参考. 一、先体验一下 比如我们想安装一个软件&…...
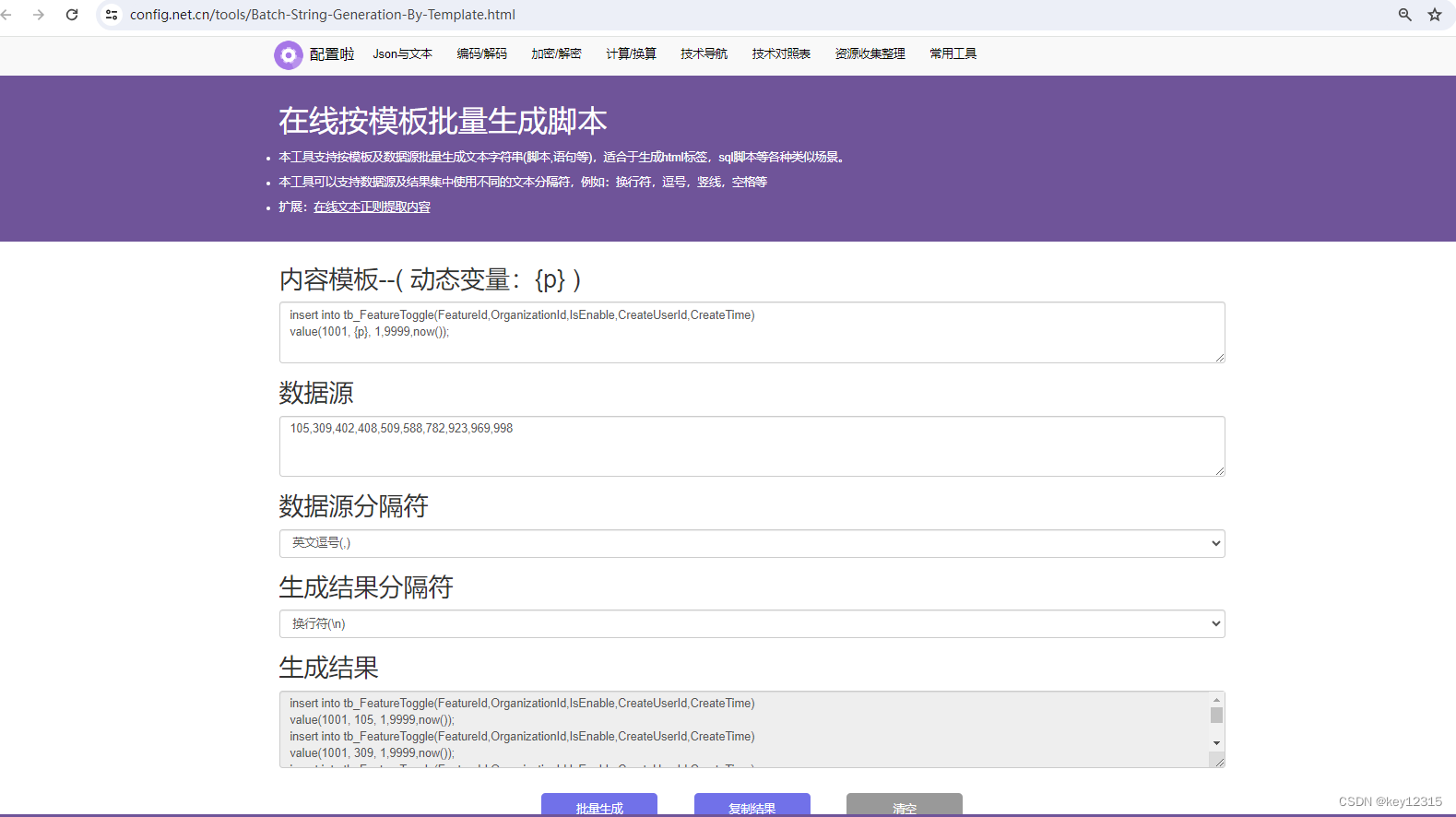
在线按模板批量生成文本工具
具体请前往:在线按模板批量生成文本工具...

Linux之关机重启
服务器除了通过界面 进行关机,重启操作,还可以通过命令的方式实现 shutdown [-t seconds] [-rkhncfF] time [message] 常用选项 参数功能-t seconds设定在几秒钟之后进行关机程序-k并不会真的关机,只是将警告讯息传送给所有使用者-r关机后重…...
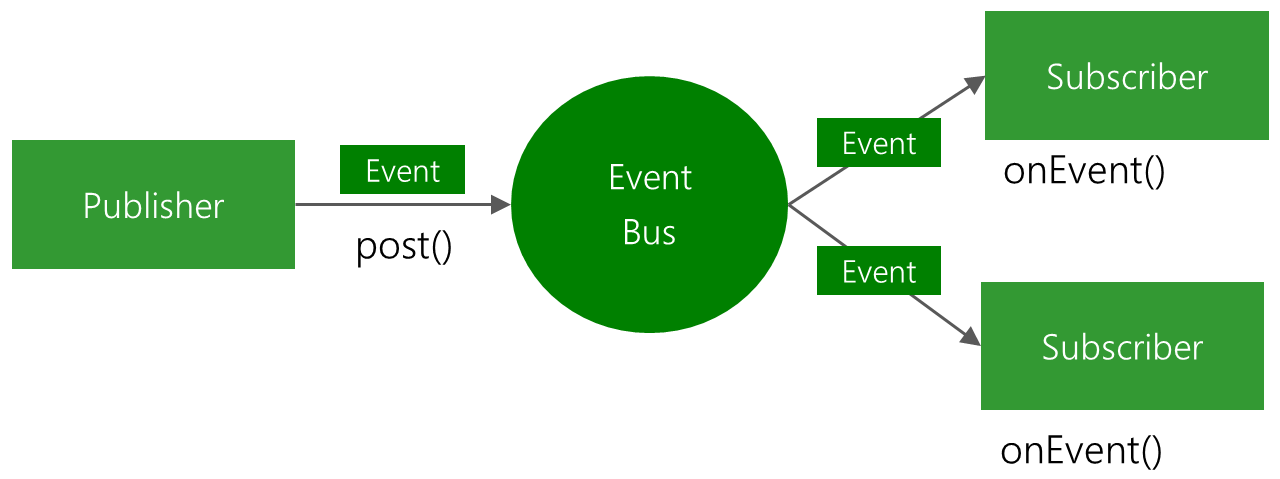
【Android】使用EventBus进行线程间通讯
EventBus 简介 EventBus:github EventBus是Android和Java的发布/订阅事件总线。 简化组件之间的通信 解耦事件发送者和接收者 在 Activities, Fragments, background threads中表现良好 避免复杂且容易出错的依赖关系和生命周期问题 Publisher使用post发出…...

Leetcode 3179. Find the N-th Value After K Seconds
Leetcode 3179. Find the N-th Value After K Seconds 1. 解题思路2. 代码实现 题目链接:3179. Find the N-th Value After K Seconds 1. 解题思路 这一题的话还是一个动态规划的问题,核心递推关系式为: dp(n, k) dp(n-1, k) dp(n, k)我…...
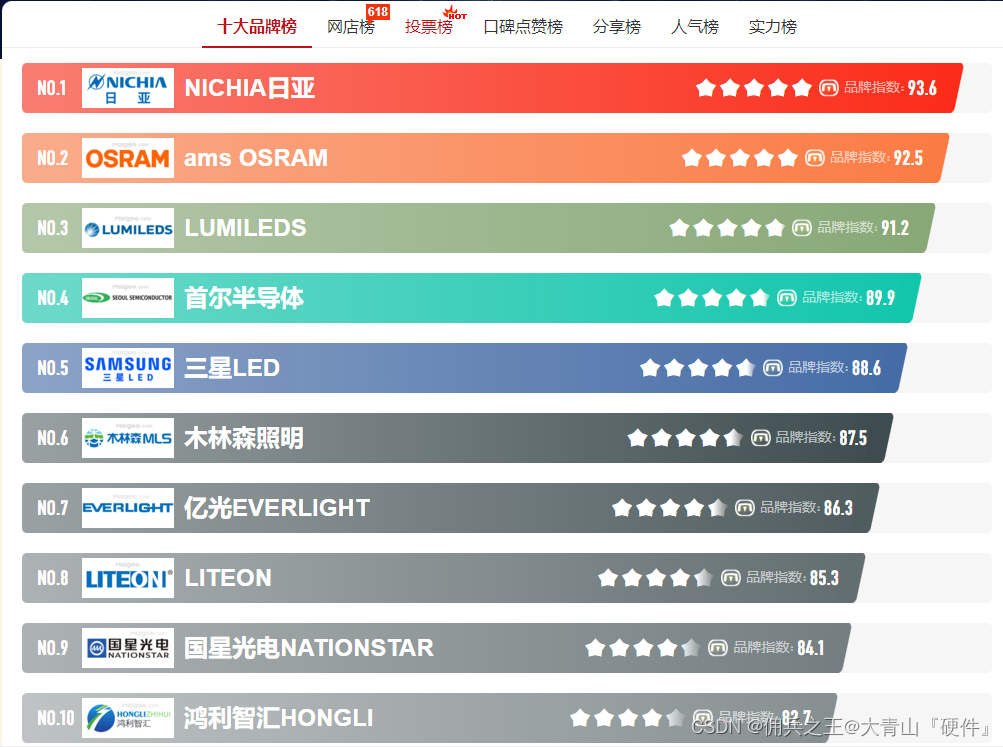
发光二极管十大品牌
日常电路设计中,LED是必用的元器件之一,辅助判定电路异常。 十大发光二极管品牌-LED灯珠生产厂家哪家好-LED发光二极管厂家前十-Maigoo品牌榜...

nginx配置文件
Nginx是一个高性能的HTTP和反向代理服务器,它的配置文件是其灵活性和强大功能的核心。Nginx的配置文件通常位于 /etc/nginx/nginx.conf 或者 /usr/local/nginx/conf/nginx.conf,取决于你的操作系统和安装路径。配置文件的结构和语法决定了Nginx如何处理请…...
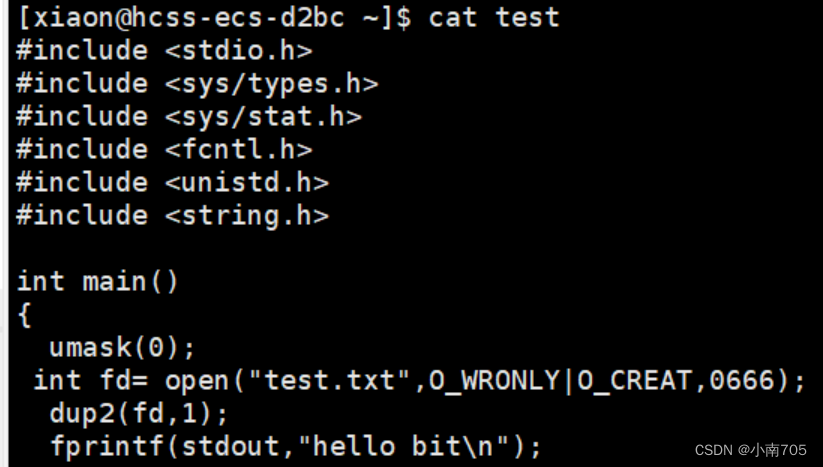
Linux基础I/O
一,系统文件I/O 写文件: #include <stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <unistd.h> #include <string.h> int main() {umask(0);int fd open("myfile", O_WRO…...

视觉SLAM14精讲——相机与图像3.1
视觉SLAM14精讲 三维空间刚体运动1.0三维空间刚体运动1.1三维空间刚体运动1.2李群与李代数2.1相机与图像3.1 视觉SLAM14精讲——相机与图像3.1 视觉SLAM14精讲简介相机模型内参K 简介 相机是VSLAM中的核心传感器。本章知识点内容涉及到相机相关的知识以及3D计算视觉的一些基础…...
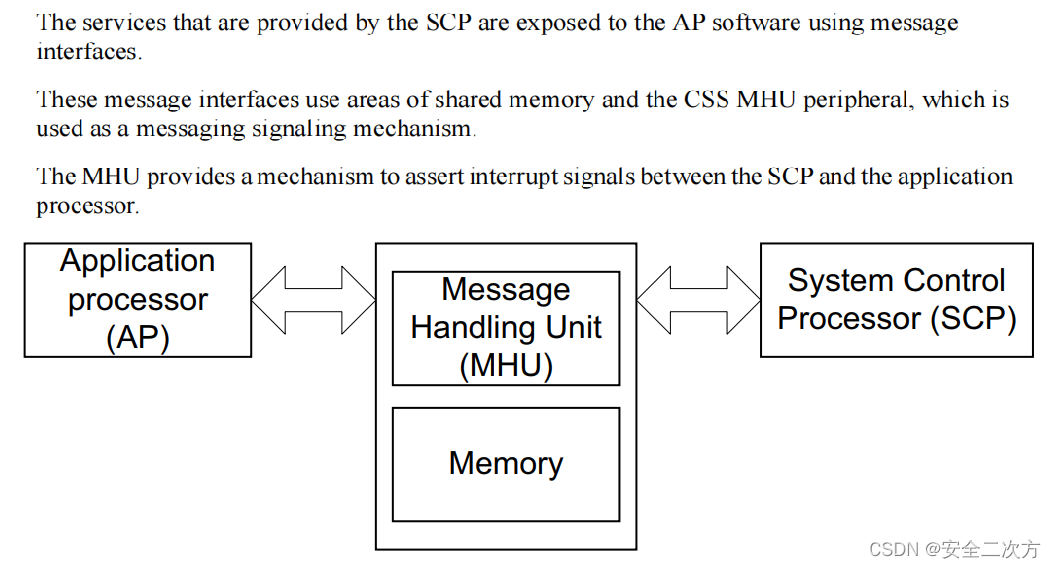
ARM功耗管理框架之SCP
安全之安全(security)博客目录导读 目录 一、功耗管理框架中的SCP 二、SCP的示例 三、SCP固件 四、SCP启动流程 五、SCP的memory map 六、SCP与AP的通信 思考:功耗管理框架?SCP?PPU?LPI?之间的关系?…...

uni-app学习--基础组件使用、页面生命周期、本地存储、网络请求、条件编译、路由跳转
文章目录 1. 基本组件的使用1. text文本组件的使用2. view视图容器组件的使用3. button按钮组件的使用4. image组件的使用5. map组件 2. uni-app中的样式1. uni-app:px2rpx计算 3. uni-app的数据绑定1. 基本的数据绑定2. v-bind,v-for,v-on 4. uni-app的生命周期1. …...

Cweek4+5
C语言学习 十.指针详解 6.有关函数指针的代码 代码1:(*(void (*)())0)(); void(*)()是函数指针类型,0是一个函数的地址 (void(*)())是强制转换 总的是调用0地址处的函数,传入参数为空 代码2:void (*signal(int, void(*)(int))…...

Segment Anything CSharp| 在 C# 中通过 OpenVINO™ 部署 SAM 模型实现万物分割
OpenVINO™ C# API 是一个 OpenVINO™ 的 .Net wrapper,应用最新的 OpenVINO™ 库开发,通过 OpenVINO™ C API 实现 .Net 对 OpenVINO™ Runtime 调用.Segment Anything Model(SAM)是一个基于Transformer的深度学习模型&#x…...

企业应如何选择安全合规的内外网文件摆渡系统?
网络隔离是一种安全措施,旨在将网络划分为不同的部分,以减少安全风险并保护敏感信息。常见的隔离方式像物理隔离、逻辑隔离、防火墙隔离、虚拟隔离、DMZ区隔离等,将网络隔离成内网和外网。内外网文件摆渡通常指在内部网络(内网&am…...

一分钟有60秒,这个有趣的原因你知道吗?
每周跟踪AI热点新闻动向和震撼发展 想要探索生成式人工智能的前沿进展吗?订阅我们的简报,深入解析最新的技术突破、实际应用案例和未来的趋势。与全球数同行一同,从行业内部的深度分析和实用指南中受益。不要错过这个机会,成为AI领…...
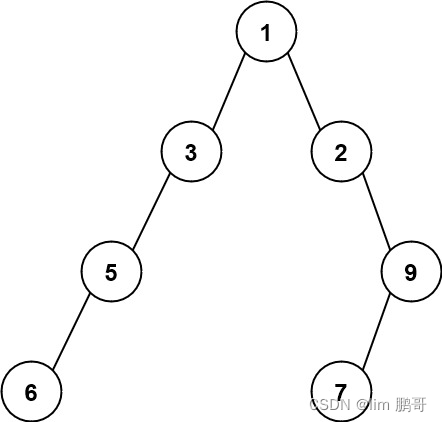
二叉树最大宽度
文章目录 前言二叉树最大宽度1.题目解析2.算法原理3.代码编写 总结 前言 二叉树最大宽度 1.题目解析 给你一棵二叉树的根节点 root ,返回树的 最大宽度 。 树的 最大宽度 是所有层中最大的 宽度 。 每一层的 宽度 被定义为该层最左和最右的非空节点(即…...
自定义HOOK)
React@16.x(24)自定义HOOK
目录 1,介绍2,简单举例2.1,获取数据1.2,计时器 2,自定义 HOOK 相比类组件 1,介绍 将一些常用的,跨组件的函数抽离,做成公共函数也就是 HOOK。自定义HOOK需要按照HOOK的规则来实现&a…...

群体优化算法----树蛙优化算法介绍以及应用于资源分配示例
介绍 树蛙优化算法(Tree Frog Optimization Algorithm, TFO)是一种基于群体智能的优化算法,模拟了树蛙在自然环境中的跳跃和觅食行为。该算法通过模拟树蛙在树枝间的跳跃来寻找最优解,属于近年来发展起来的自然启发式算法的一种 …...

常见汇编指令
下面是一些包含汇编指令 MOV、PUSH、POP、LEA、LDS、ADD、ADC、INC、SUB、SBB、DEC、CMP、MUL、DIV、AND、OR、XOR、NOT、TEST、SHL、SAL、SHR、SAR、ROL、ROR、RCL、RCR、LODS、MOVS 的例题。这些例题展示了每条指令的用法及其作用。 1. MOV 指令 MOV AX, BX ; 将寄存器 B…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

2021-03-15 iview一些问题
1.iview 在使用tree组件时,发现没有set类的方法,只有get,那么要改变tree值,只能遍历treeData,递归修改treeData的checked,发现无法更改,原因在于check模式下,子元素的勾选状态跟父节…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

HashMap中的put方法执行流程(流程图)
1 put操作整体流程 HashMap 的 put 操作是其最核心的功能之一。在 JDK 1.8 及以后版本中,其主要逻辑封装在 putVal 这个内部方法中。整个过程大致如下: 初始判断与哈希计算: 首先,putVal 方法会检查当前的 table(也就…...

【LeetCode】算法详解#6 ---除自身以外数组的乘积
1.题目介绍 给定一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。 题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。 请 不要使用除法,且在 O…...
