[Algorithm][动态规划][01背包问题][目标和][最后一块石头的重量Ⅱ]详细讲解
目录
- 1.目标和
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
- 2.最后一块石头的重量 II
- 1.题目链接
- 2.算法原理详解
- 3.代码实现
1.目标和
1.题目链接
- 目标和
2.算法原理详解
-
问题转化:在数组中选择一些数,让这些数的和等于
a,一共有多少种选法?–> 01背包
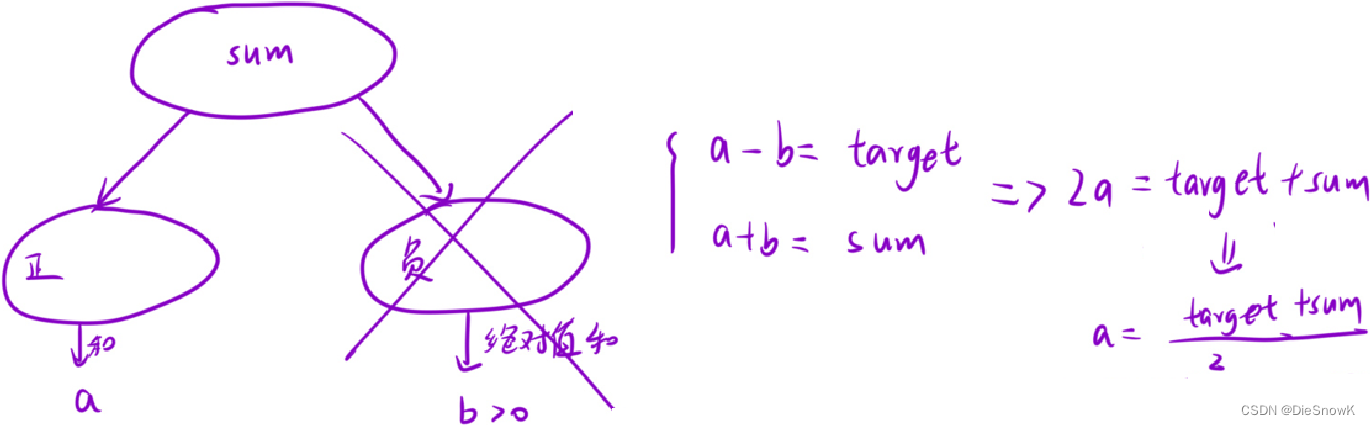
-
思路:
-
确定状态表示 ->
dp[i][j]的含义dp[i]j]:从前i个数中**选**,总和正好等于j,一共有多少种选法
-
推导状态转移方程:根据最后一个位置的情况,分情况讨论
dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i]]

-
初始化:
- 多开一行及一列虚拟结点
- 第一列除
[0, 0],其余无需初始化- 这里第一列不会越界访问,可以交给DP阶段处理
- 因为只有
dp[i - 1][j - nums[i]]可能越界访问- 但是在判定后,只有
j == nums[i] == 0的情况,才会进入第一列,此时又不会越界 - 如果不符合条件,就不会进来,也不会触发越界访问

- 但是在判定后,只有
-
确定填表顺序:从上往下
-
确定返回值:
dp[n][a]
-
-
滚动数字优化同[模板] 背包
3.代码实现
// v1.0
int findTargetSumWays(vector<int>& nums, int target)
{// 问题转换int sum = 0;for(auto& x : nums){sum += x;}int aim = (sum + target) / 2;// 边界处理if(aim < 0 || (sum + target) % 2) return 0;int n = nums.size();vector<vector<int>> dp(n + 1, vector<int>(aim + 1));dp[0][0] = 1;for(int i = 1; i <= n; i++){for(int j = 0; j <= aim; j++) // 第一列没有初始化,也在DP阶段处理{dp[i][j] = dp[i - 1][j];if(j >= nums[i - 1]){dp[i][j] += dp[i - 1][j - nums[i - 1]];}}}return dp[n][aim];
}
-----------------------------------------------------------------------
// v2.0 滚动数组优化
int findTargetSumWays(vector<int>& nums, int target)
{// 问题转换int sum = 0;for(auto& x : nums){sum += x;}int aim = (sum + target) / 2;// 边界处理if(aim < 0 || (sum + target) % 2) return 0;int n = nums.size();vector<int> dp(aim + 1);dp[0] = 1;for(int i = 1; i <= n; i++){for(int j = aim; j >= nums[i - 1]; j--){dp[j] += dp[j - nums[i - 1]];}}return dp[aim];
}
2.最后一块石头的重量 II
1.题目链接
- 最后一块石头的重量 II
2.算法原理详解
-
问题转化:在数组中选择一些数,让这些数的和尽可能接近
sum / 2- 问题转化成了目标和–> 01背包
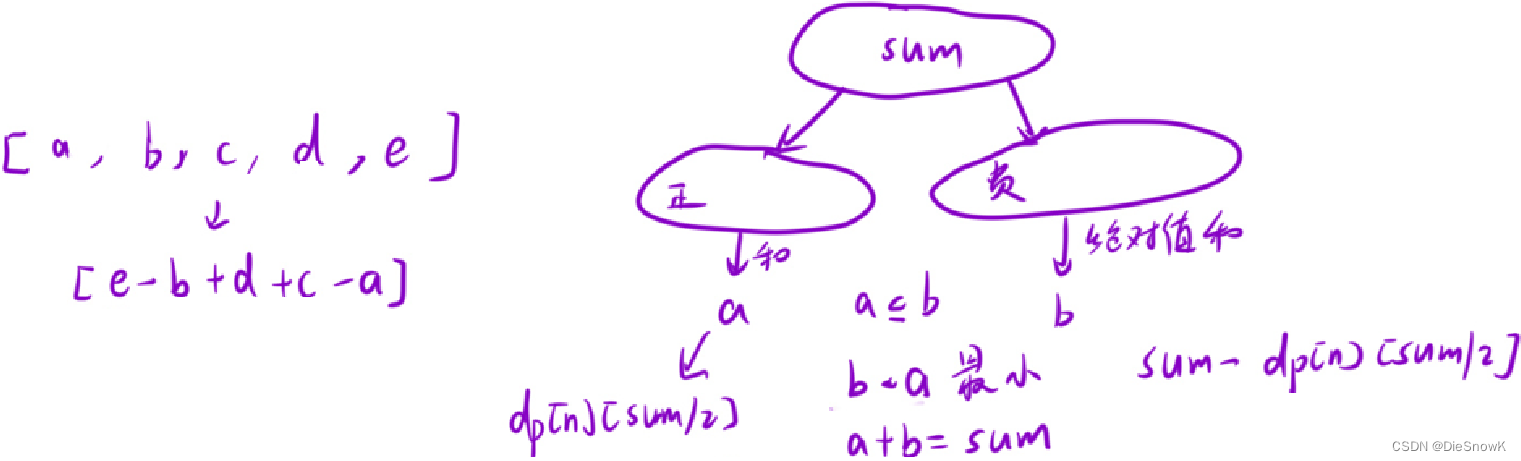
- 问题转化成了目标和–> 01背包
-
思路:
-
确定状态表示 ->
dp[i][j]的含义dp[i]j]:从前i个数中**选**,总和不超过j,此时的最大和
-
推导状态转移方程:根据最后一个位置的情况,分情况讨论
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - nums[i]] + nums[i])
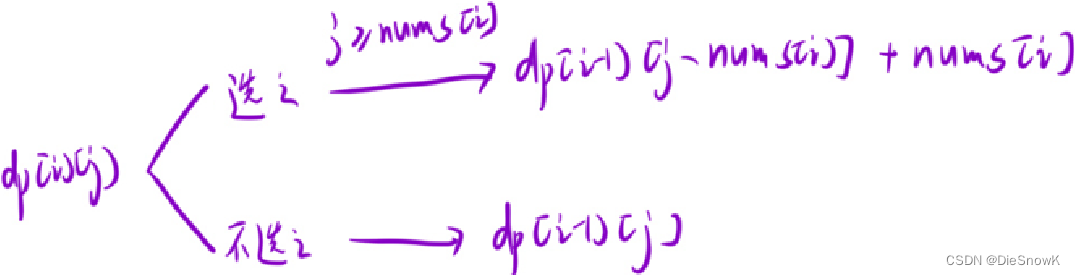
-
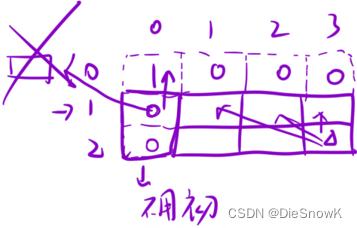
初始化:
- 多开一行及一列虚拟结点
- 第一列除
[0, 0],其余无需初始化- 这里第一列不会越界访问,可以交给DP阶段处理
- 因为只有
dp[i - 1][j - stones[i - 1]]可能越界访问- 但是在判定后,只有
j == stones[i - 1] == 0的情况,才会进入第一列,此时又不会越界 - 如果不符合条件,就不会进来,也不会触发越界访问
- 但是在判定后,只有
-
确定填表顺序:从上往下
-
确定返回值:
sum - 2 * dp[n][sum / 2]
-
-
滚动数字优化同[模板] 背包
3.代码实现
// v1.0
int lastStoneWeightII(vector<int>& stones)
{int sum = 0;for(auto& x : stones){sum += x;}int n = stones.size(), m = sum / 2;vector<vector<int>> dp(n + 1, vector<int>(m + 1));for(int i = 1; i <= n; i++){for(int j = 0; j <= m; j++){dp[i][j] = dp[i - 1][j];if(j >= stones[i - 1]){dp[i][j] = max(dp[i][j], dp[i - 1][j - stones[i - 1]] + stones[i - 1]);}}}return sum - 2 * dp[n][m];
}
-----------------------------------------------------------------------
// v2.0 滚动数组优化
int lastStoneWeightII(vector<int>& stones)
{int sum = 0;for(auto& x : stones){sum += x;}int n = stones.size(), m = sum / 2;vector<int> dp(m + 1);for(int i = 1; i <= n; i++){for(int j = m; j >= stones[i - 1]; j--){dp[j] = max(dp[j], dp[j - stones[i - 1]] + stones[i - 1]);}}return sum - 2 * dp[m];
}
相关文章:

[Algorithm][动态规划][01背包问题][目标和][最后一块石头的重量Ⅱ]详细讲解
目录 1.目标和1.题目链接2.算法原理详解3.代码实现 2.最后一块石头的重量 II1.题目链接2.算法原理详解3.代码实现 1.目标和 1.题目链接 目标和 2.算法原理详解 问题转化:在数组中选择一些数,让这些数的和等于a,一共有多少种选法?…...
LabVIEW控制PLC的实现方式
LabVIEW与PLC的结合可以充分发挥两者的优点,实现更高效、灵活和可靠的自动化控制系统。本文将详细介绍LabVIEW控制PLC的实现方式,包括通信接口、数据交换、编程方法及实际应用案例,帮助用户理解并应用这一技术。 通信接口 常见通信协议 La…...
JSTL知识点讲解与配置
JSTL(JavaServer Pages Standard Tag Library)是Java EE平台中的一个标准库,提供了一组用于在JSP(JavaServer Pages)中简化和标准化常见任务的标签。这些标签封装了很多常见的JSP功能,可以使得JSP页面更加简…...

Autodesk 3ds Max软件下载安装;3ds Max功能强大的三维建模、渲染软件安装包获取
3ds Max,无论是初学者还是资深设计师,都能通过3ds Max在数字世界中实现自己的创意,打造出令人惊叹的三维作品。 在3ds Max中,灯光系统是至关重要的一环。它提供了光度学灯光和标准灯光两种主要类型,用于照亮和增强场景…...
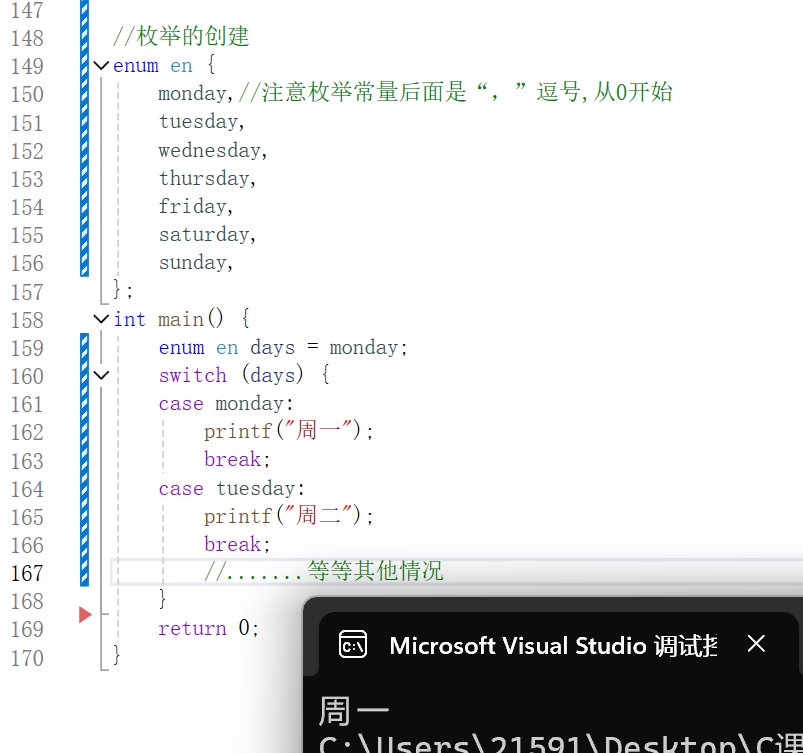
联合体和枚举<C语言>
导言 在C语言中除了结构体外,联合体和枚举也是自定义类型,联合体主要用于节省空间,在同一块内存存储多种类型的数据,而枚举可以提高代码的可读性、可维护性。 联合体(union) 它还有个更容易理解的名字&…...

算法人生(21):从“React框架”看“情绪管理”
说起React框架,我们知道它是一种由Facebook开发和维护的开源JavaScript库,主要用于构建用户界面,特别是单页应用程序(SPA)。React框架围绕组件化,即把用户界面拆分为可复用的独立组件,每个组件负…...

千益畅行:合法合规的旅游卡服务,真实可靠的旅游体验
近期,关于千益畅行旅游卡服务的讨论引起了广泛关注。然而,网络上出现了一些对其误解和质疑的声音。为了澄清事实,我们深入了解了千益畅行的运营模式和业务特点,发现它是一家合法合规的旅游卡服务提供商,为消费者提供真…...
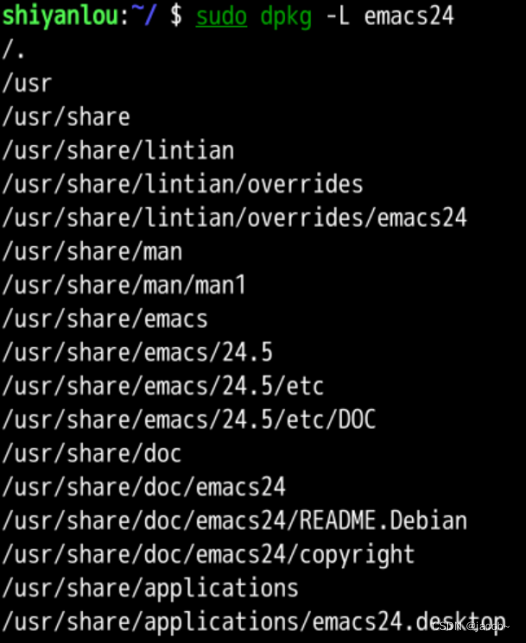
Linux下软件安装
提示:制作不易,可以点个关注和收藏哦。 前言 介绍 Ubuntu 下软件安装的几种方式,及 apt,dpkg 工具的使用。 提示:以下是本篇文章正文内容,下面案例可供参考. 一、先体验一下 比如我们想安装一个软件&…...
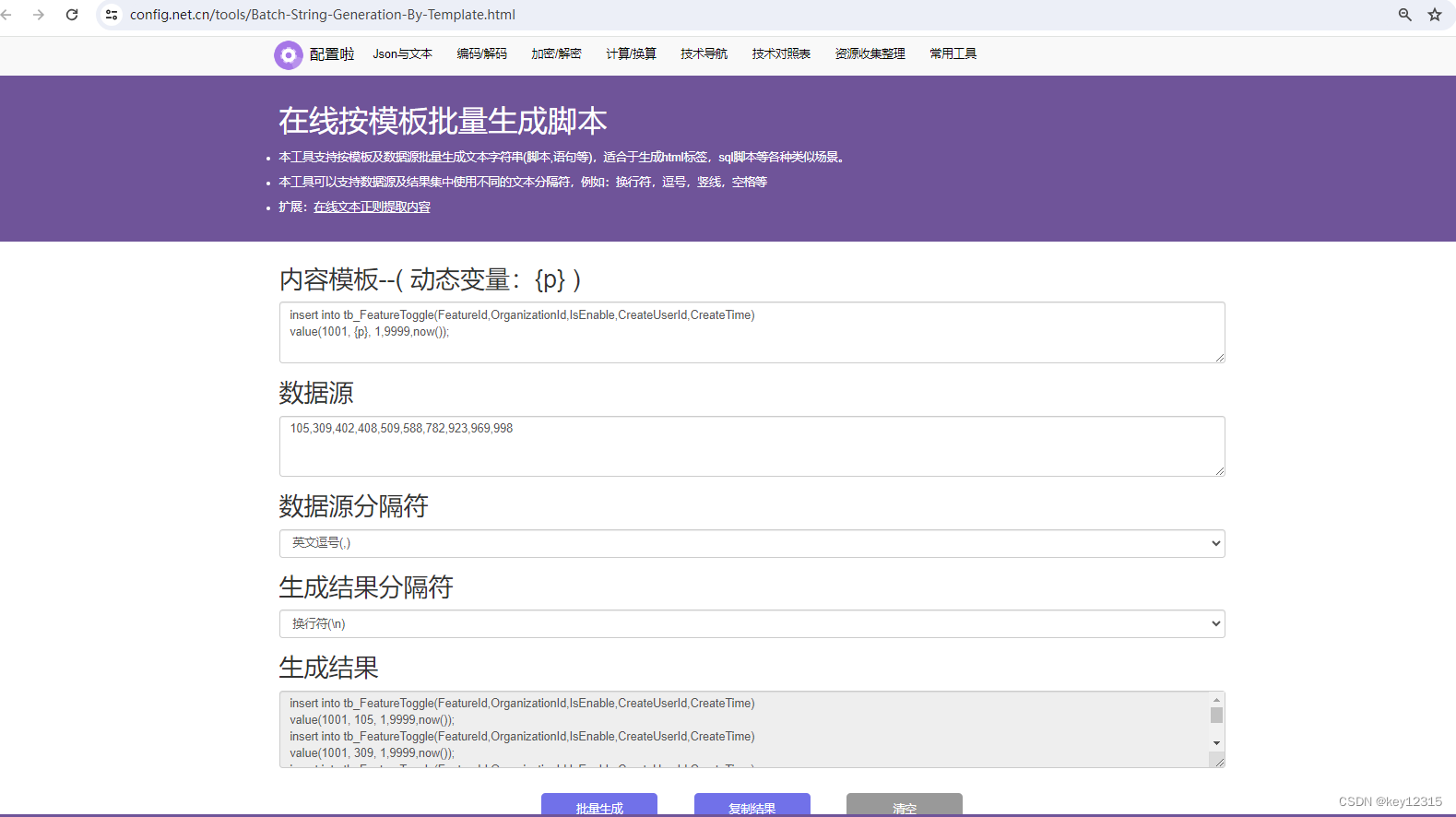
在线按模板批量生成文本工具
具体请前往:在线按模板批量生成文本工具...

Linux之关机重启
服务器除了通过界面 进行关机,重启操作,还可以通过命令的方式实现 shutdown [-t seconds] [-rkhncfF] time [message] 常用选项 参数功能-t seconds设定在几秒钟之后进行关机程序-k并不会真的关机,只是将警告讯息传送给所有使用者-r关机后重…...
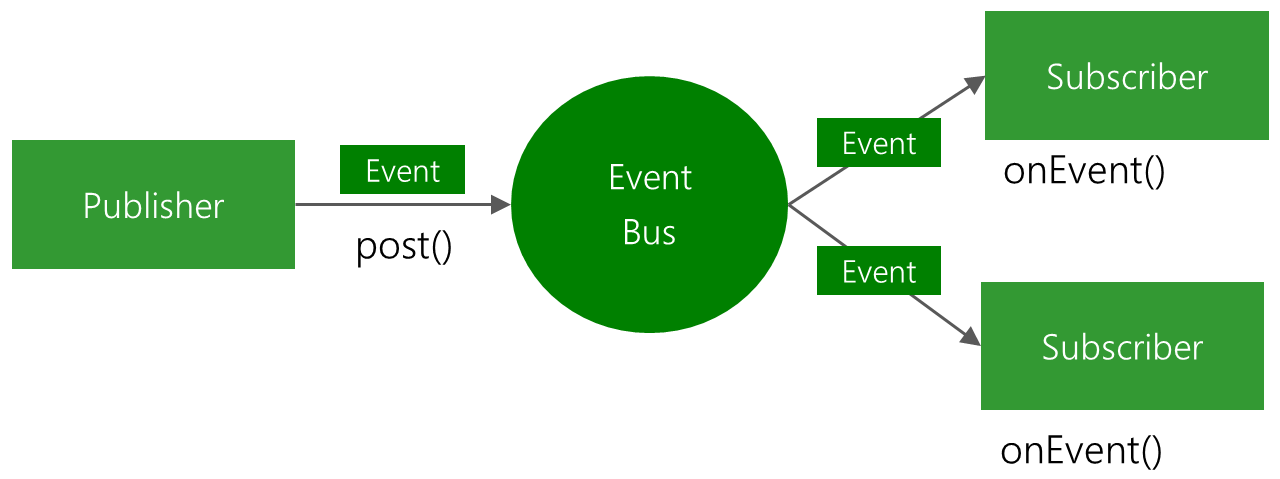
【Android】使用EventBus进行线程间通讯
EventBus 简介 EventBus:github EventBus是Android和Java的发布/订阅事件总线。 简化组件之间的通信 解耦事件发送者和接收者 在 Activities, Fragments, background threads中表现良好 避免复杂且容易出错的依赖关系和生命周期问题 Publisher使用post发出…...

Leetcode 3179. Find the N-th Value After K Seconds
Leetcode 3179. Find the N-th Value After K Seconds 1. 解题思路2. 代码实现 题目链接:3179. Find the N-th Value After K Seconds 1. 解题思路 这一题的话还是一个动态规划的问题,核心递推关系式为: dp(n, k) dp(n-1, k) dp(n, k)我…...
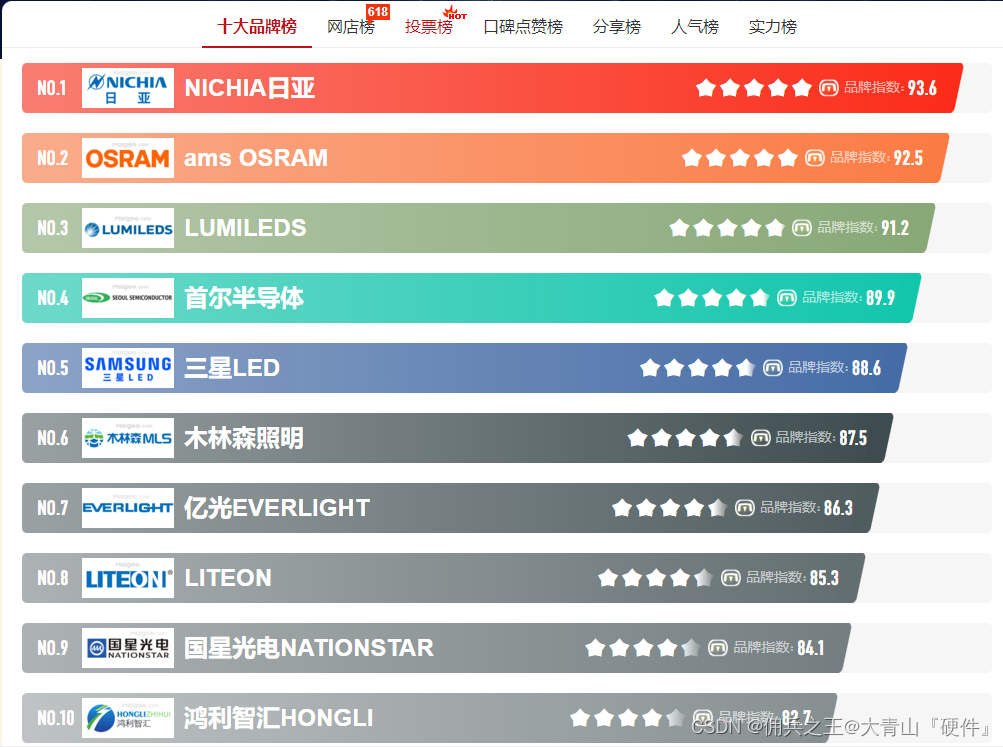
发光二极管十大品牌
日常电路设计中,LED是必用的元器件之一,辅助判定电路异常。 十大发光二极管品牌-LED灯珠生产厂家哪家好-LED发光二极管厂家前十-Maigoo品牌榜...

nginx配置文件
Nginx是一个高性能的HTTP和反向代理服务器,它的配置文件是其灵活性和强大功能的核心。Nginx的配置文件通常位于 /etc/nginx/nginx.conf 或者 /usr/local/nginx/conf/nginx.conf,取决于你的操作系统和安装路径。配置文件的结构和语法决定了Nginx如何处理请…...
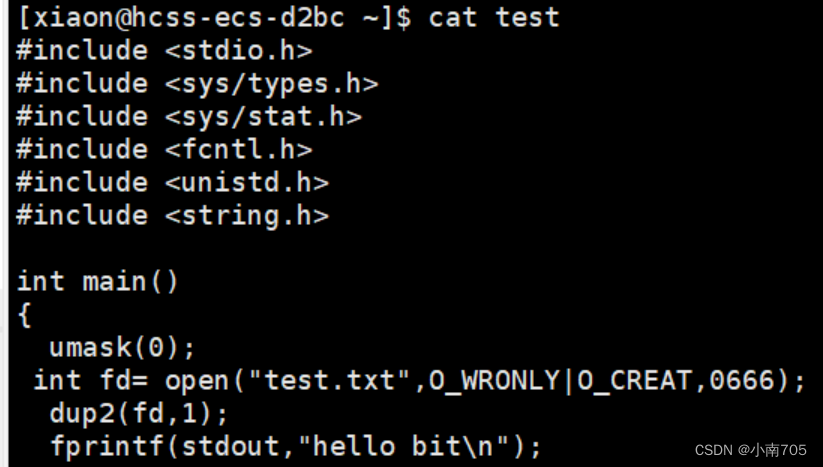
Linux基础I/O
一,系统文件I/O 写文件: #include <stdio.h> #include <sys/types.h> #include <sys/stat.h> #include <fcntl.h> #include <unistd.h> #include <string.h> int main() {umask(0);int fd open("myfile", O_WRO…...

视觉SLAM14精讲——相机与图像3.1
视觉SLAM14精讲 三维空间刚体运动1.0三维空间刚体运动1.1三维空间刚体运动1.2李群与李代数2.1相机与图像3.1 视觉SLAM14精讲——相机与图像3.1 视觉SLAM14精讲简介相机模型内参K 简介 相机是VSLAM中的核心传感器。本章知识点内容涉及到相机相关的知识以及3D计算视觉的一些基础…...
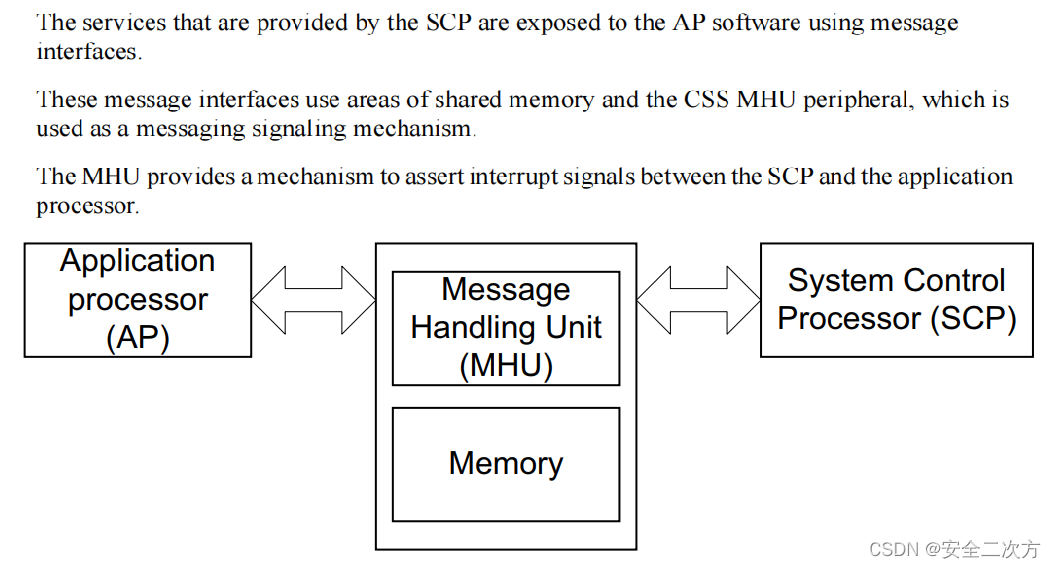
ARM功耗管理框架之SCP
安全之安全(security)博客目录导读 目录 一、功耗管理框架中的SCP 二、SCP的示例 三、SCP固件 四、SCP启动流程 五、SCP的memory map 六、SCP与AP的通信 思考:功耗管理框架?SCP?PPU?LPI?之间的关系?…...

uni-app学习--基础组件使用、页面生命周期、本地存储、网络请求、条件编译、路由跳转
文章目录 1. 基本组件的使用1. text文本组件的使用2. view视图容器组件的使用3. button按钮组件的使用4. image组件的使用5. map组件 2. uni-app中的样式1. uni-app:px2rpx计算 3. uni-app的数据绑定1. 基本的数据绑定2. v-bind,v-for,v-on 4. uni-app的生命周期1. …...

Cweek4+5
C语言学习 十.指针详解 6.有关函数指针的代码 代码1:(*(void (*)())0)(); void(*)()是函数指针类型,0是一个函数的地址 (void(*)())是强制转换 总的是调用0地址处的函数,传入参数为空 代码2:void (*signal(int, void(*)(int))…...

Segment Anything CSharp| 在 C# 中通过 OpenVINO™ 部署 SAM 模型实现万物分割
OpenVINO™ C# API 是一个 OpenVINO™ 的 .Net wrapper,应用最新的 OpenVINO™ 库开发,通过 OpenVINO™ C API 实现 .Net 对 OpenVINO™ Runtime 调用.Segment Anything Model(SAM)是一个基于Transformer的深度学习模型&#x…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

FastAPI 教程:从入门到实践
FastAPI 是一个现代、快速(高性能)的 Web 框架,用于构建 API,支持 Python 3.6。它基于标准 Python 类型提示,易于学习且功能强大。以下是一个完整的 FastAPI 入门教程,涵盖从环境搭建到创建并运行一个简单的…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

分布式增量爬虫实现方案
之前我们在讨论的是分布式爬虫如何实现增量爬取。增量爬虫的目标是只爬取新产生或发生变化的页面,避免重复抓取,以节省资源和时间。 在分布式环境下,增量爬虫的实现需要考虑多个爬虫节点之间的协调和去重。 另一种思路:将增量判…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
