【一百零八】【算法分析与设计】P1908 逆序对,P1637 三元上升子序列,树状数组区间和应用
P1908 逆序对
逆序对
题目描述
猫猫 TOM 和小老鼠 JERRY 最近又较量上了,但是毕竟都是成年人,他们已经不喜欢再玩那种你追我赶的游戏,现在他们喜欢玩统计。
最近,TOM 老猫查阅到一个人类称之为“逆序对”的东西,这东西是这样定义的:对于给定的一段正整数序列,逆序对就是序列中 a i > a j a_i>a_j ai>aj
且 i < j i<j i<j 的有序对。知道这概念后,他们就比赛谁先算出给定的一段正整数序列中逆序对的数目。注意序列中可能有重复数字。Update:数据已加强。
输入格式
第一行,一个数 n n n,表示序列中有 n n n个数。
第二行 n n n 个数,表示给定的序列。序列中每个数字不超过 1 0 9 10^9 109。
输出格式
输出序列中逆序对的数目。
样例 #1
样例输入 #1
6 5 4 2 6 3 1样例输出 #1
11提示
对于 25 % 25\% 25% 的数据, n ≤ 2500 n \leq 2500 n≤2500
对于 50 % 50\% 50% 的数据, n ≤ 4 × 1 0 4 n \leq 4 \times 10^4 n≤4×104。
对于所有数据, n ≤ 5 × 1 0 5 n \leq 5 \times 10^5 n≤5×105
请使用较快的输入输出
应该不会 O ( n 2 ) O(n^2) O(n2) 过 50 万吧 by chen_zhe
求解逆序对的个数,按照每一个下标对应元素,以这个元素为二元组前者所拥有的逆序对的个数.
二元组意思是下标{i,j}组合,并且满足i<j.这样作为一个二元组.arr数组中有1~n下标的元素,遍历所有位置的元素,考虑i位置元素作为二元组中,下标较小的一个,看这样的元素构成的逆序对有多少个.
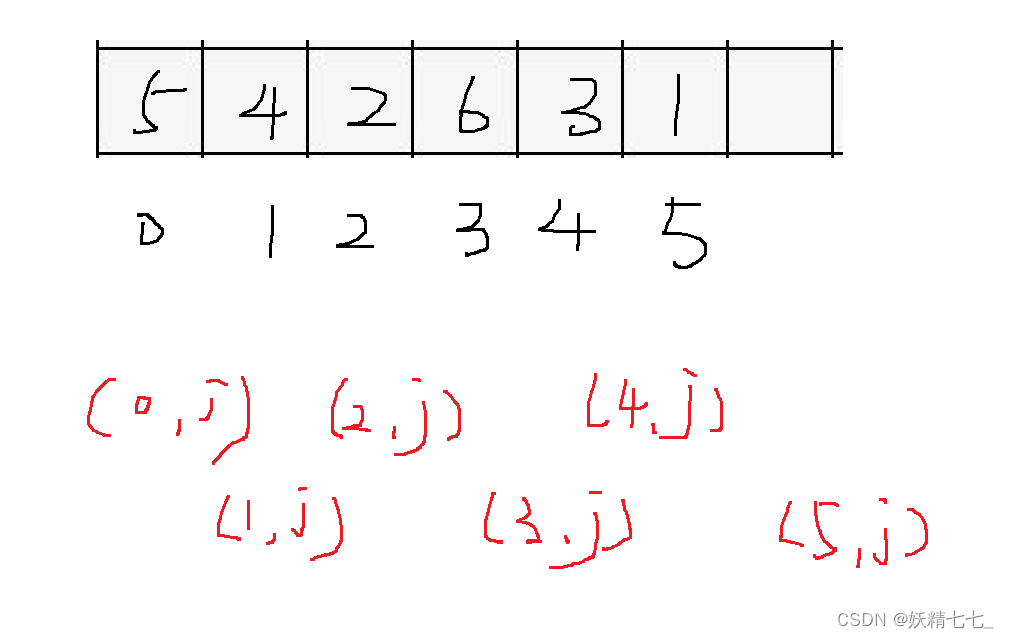
分别考虑0下标作为二元组较小下标,这样的所有二元组中的逆序对的个数.再考虑1下标作为二元组较小下标,这样的所有二元组中的逆序对的个数,依次类推,
很容易发现这样的详略可以不重不漏遍历所有的情况.
考虑i位置元素作为二元组较小下标,此时要求逆序对的个数,我们需要直到下标i+1~n区间中所有元素值小于i位置元素值的个数,个数就是逆序对的个数.
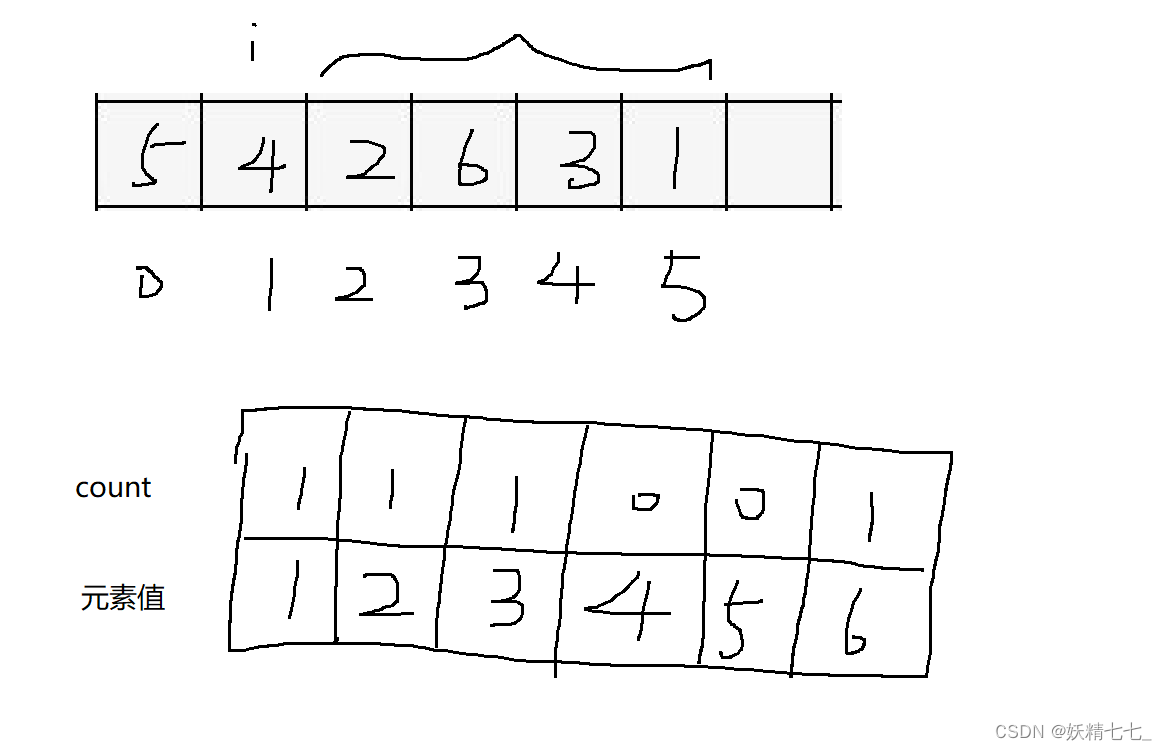
构建元素值映射个数的结构,只需要遍历<=i-1的前缀和即可.
很容易发现元素值映射个数结构,元素值可能是负数,并且不需要12345678连续的不少的元素值映射个数.
如果arr数组分别是145563,我们发现2元素值一直都没出现,所以2映射数量是可以不需要的.
因此需要做离散化操作.
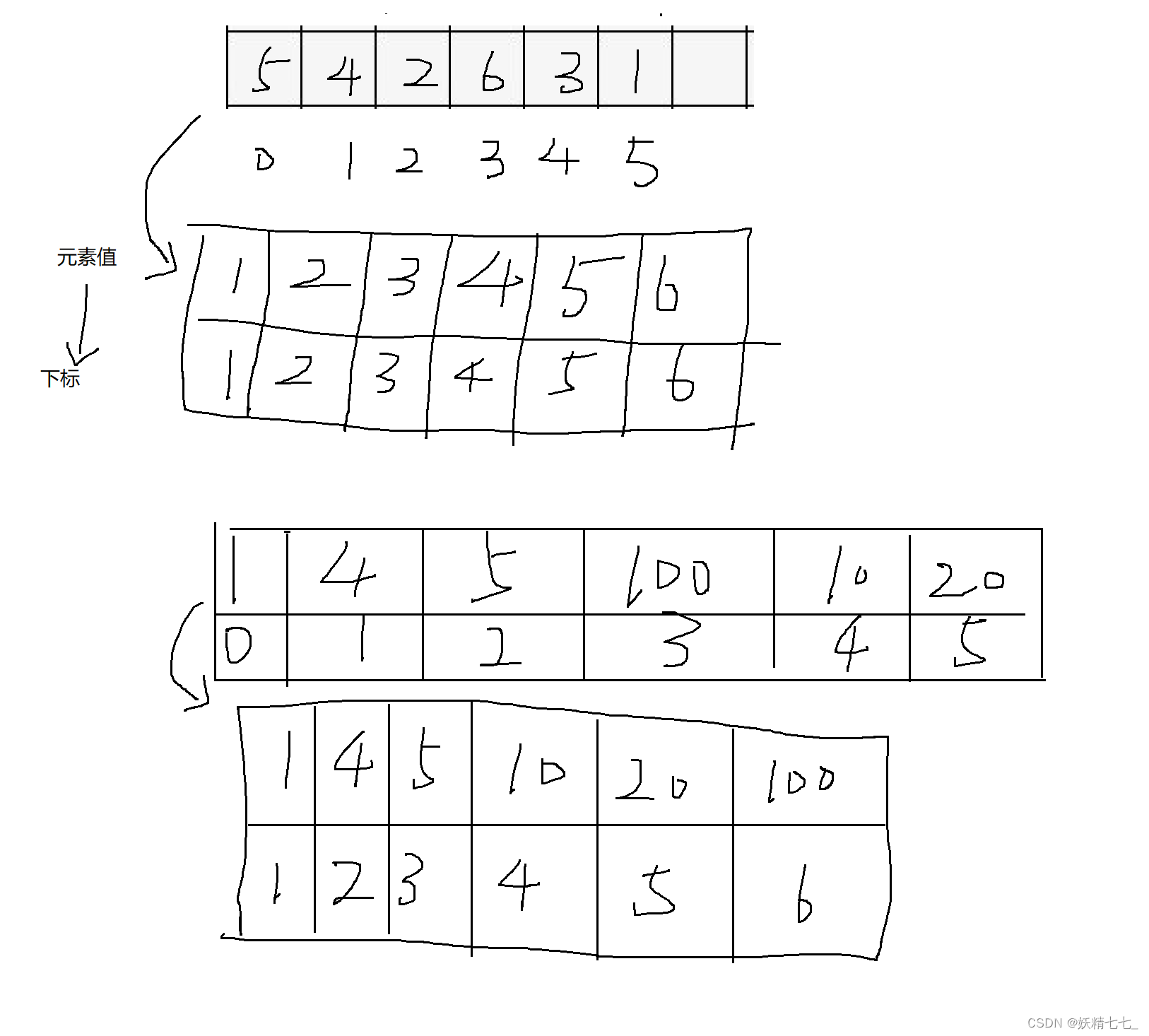
离散化操作,元素值按照从小到大排序并且去重,元素值映射下标,下标从1开始,依次对应.
只需要利用map结构,将所有的元素值加入map中,然后遍历map依次赋值second为1,2,3,…以此类推.
这样我们只需要构建index映射数量的结构,index一定是正数,并且是连续的.
从后往前遍历i位置元素,查询逆序对个数,arr[i]映射index,1~index-1的前缀和,得到的就是逆序对的个数.
更新index位置的个数.以此类推.
动态维护单点更新和区间和操作,利用树状数组.
#include<bits/stdc++.h>
using namespace std;#define int long long
#define endl '\n'int n; // 定义一个全局变量 n,表示序列中的数目
vector<int> arr; // 定义一个全局向量 arr,用来存储输入的序列
int ret; // 定义一个全局变量 ret,用来存储逆序对的数量
map<int, int> arr_index; // 定义一个全局 map,用来存储序列中每个数字的索引// 树状数组类定义
class Tree {
public:vector<int> tree; // 定义一个向量 tree,用来存储树状数组// 计算 lowbitint lowbit(int i) {return i & -i; // 返回 i 和 -i 的按位与,获取最低位的 1}// 在树状数组中增加值void add(int i, int k) {while (i <= n) { // 从索引 i 开始,向上更新树状数组tree[i] += k; // 增加 ki += lowbit(i); // 移动到下一个需要更新的位置}}// 计算前缀和int sum(int i) {int ret = 0; // 初始化结果为 0while (i > 0) { // 从索引 i 开始,向下计算前缀和ret += tree[i]; // 加上当前索引的值i -= lowbit(i); // 移动到下一个需要计算的位置}return ret; // 返回前缀和}// 计算区间和int range(int l, int r) {return sum(r) - sum(l - 1); // 返回区间 [l, r] 的和}// 默认构造函数Tree() {}// 使用给定数组构造树状数组Tree(vector<int> arr) {tree.assign(arr.size(), 0); // 初始化树状数组for (int i = 1; i <= arr.size(); i++) {add(i, arr[i]); // 将数组中的值添加到树状数组中}}
};Tree t1; // 定义一个全局的树状数组对象// 主解题函数
void solve() {ret = 0; // 初始化逆序对数量为 0t1.tree.assign(n + 5, 0); // 初始化树状数组的大小int index = 1; // 初始化索引为 1for (auto& xx : arr_index) {xx.second = index++; // 给每个数字分配一个唯一的索引}for (int i = n; i >= 1; i--) {int index = arr_index[arr[i]]; // 获取当前数字的索引ret += t1.sum(index - 1); // 计算比当前数字小的数字的数量t1.add(index, 1); // 在树状数组中增加当前数字}cout << ret << endl; // 输出逆序对数量
}signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 快速输入输出cin >> n; // 读取序列的长度arr.assign(n + 5, 0); // 初始化序列数组for (int i = 1; i <= n; i++) {cin >> arr[i]; // 读取序列中的每个数字arr_index[arr[i]]; // 在 map 中记录每个数字}solve(); // 调用解题函数
}P1637 三元上升子序列
三元上升子序列
题目描述
Erwin 最近对一种叫
thair的东西巨感兴趣。。。在含有 n n n 个整数的序列 a 1 , a 2 , … , a n a_1,a_2,\ldots,a_n a1,a2,…,an 中,三个数被称作
thair当且仅当 i < j < k i<j<k i<j<k 且
a i < a j < a k a_i<a_j<a_k ai<aj<ak。求一个序列中
thair的个数。输入格式
开始一行一个正整数 n n n,
以后一行 n n n 个整数 a 1 , a 2 , … , a n a_1,a_2,\ldots,a_n a1,a2,…,an。
输出格式
一行一个整数表示
thair的个数。样例 #1
样例输入 #1
4 2 1 3 4样例输出 #1
2样例 #2
样例输入 #2
5 1 2 2 3 4样例输出 #2
7提示
样例2 解释
7 7 7 个
thair分别是:
- 1 2 3
- 1 2 4
- 1 2 3
- 1 2 4
- 1 3 4
- 2 3 4
- 2 3 4
数据规模与约定
- 对于 30 % 30\% 30% 的数据 保证 n ≤ 100 n\le100 n≤100;
- 对于 60 % 60\% 60% 的数据 保证 n ≤ 2000 n\le2000 n≤2000;
- 对于 100 % 100\% 100% 的数据 保证 1 ≤ n ≤ 3 × 1 0 4 1 \leq n\le3\times10^4 1≤n≤3×104, 1 ≤ a i ≤ 1 0 5 1\le a_i\leq 10^5 1≤ai≤105。
递增三元组,遍历每一个位置元素i,i作为三元组最右侧的k下标,最大的下标,此时拥有的递增三元组的个数.
等价于求1~i-1位置小于我当前位置元素值的递增二元组的个数.
如果一个数组存储1~i-1映射二元组个数,只需要i求前缀和.
维护二元组数组,遍历每一个位置元素i,作为二元组较大的下标,此时拥有的二元组的个数是1~i-1中有多少个比我小的元素个数.
利用上一道题的思路可以利用数组数组求1~i-1中有多少比我小的元素个数.
#include<bits/stdc++.h>
using namespace std;#define int long long // 定义 int 为 long long 类型,方便处理大数
#define endl '\n' // 定义换行符为 endl,方便输出int n; // 定义全局变量 n,表示序列中的数目
vector<int> arr; // 定义全局向量 arr,用于存储输入的序列
int ret; // 定义全局变量 ret,用于存储三元上升子序列的数量
map<int, int> arr_index; // 定义全局 map,用于存储序列中每个数字的索引// 树状数组类定义
class Tree {
public:vector<int> tree; // 定义一个向量 tree,用于存储树状数组// 计算 lowbitint lowbit(int i) {return i & -i; // 返回 i 和 -i 的按位与,获取最低位的 1}// 在树状数组中增加值void add(int i, int k) {while (i <= n) { // 从索引 i 开始,向上更新树状数组tree[i] += k; // 增加 ki += lowbit(i); // 移动到下一个需要更新的位置}}// 计算前缀和int sum(int i) {int ret = 0; // 初始化结果为 0while (i > 0) { // 从索引 i 开始,向下计算前缀和ret += tree[i]; // 加上当前索引的值i -= lowbit(i); // 移动到下一个需要计算的位置}return ret; // 返回前缀和}// 计算区间和int range(int l, int r) {return sum(r) - sum(l - 1); // 返回区间 [l, r] 的和}// 默认构造函数Tree() {}// 使用给定数组构造树状数组Tree(vector<int> arr) {tree.assign(arr.size(), 0); // 初始化树状数组for (int i = 1; i <= arr.size(); i++) {add(i, arr[i]); // 将数组中的值添加到树状数组中}}
};Tree t1, t2; // 定义两个全局的树状数组对象// 主解题函数
void solve() {t1.tree.assign(n + 5, 0); // 初始化第一个树状数组的大小t2.tree.assign(n + 5, 0); // 初始化第二个树状数组的大小int index = 1; // 初始化索引为 1for (auto& xx : arr_index) {xx.second = index++; // 给每个数字分配一个唯一的索引}ret = 0; // 初始化三元上升子序列的数量为 0for (int i = 1; i <= n; i++) {int index = arr_index[arr[i]]; // 获取当前数字的索引t1.add(index, 1); // 在第一个树状数组中增加当前数字t2.add(index, t1.sum(index - 1)); // 在第二个树状数组中增加当前数字左侧比它小的数字的数量ret += t2.sum(index - 1); // 累加比当前数字小的数字的数量,得到三元上升子序列的数量}cout << ret << endl; // 输出三元上升子序列的数量
}signed main() {ios::sync_with_stdio(0), cin.tie(0), cout.tie(0); // 快速输入输出cin >> n; // 读取序列的长度arr.assign(n + 5, 0); // 初始化序列数组for (int i = 1; i <= n; i++) {cin >> arr[i]; // 读取序列中的每个数字arr_index[arr[i]]; // 在 map 中记录每个数字}solve(); // 调用解题函数
}结尾
最后,感谢您阅读我的文章,希望这些内容能够对您有所启发和帮助。如果您有任何问题或想要分享您的观点,请随时在评论区留言。
同时,不要忘记订阅我的博客以获取更多有趣的内容。在未来的文章中,我将继续探讨这个话题的不同方面,为您呈现更多深度和见解。
谢谢您的支持,期待与您在下一篇文章中再次相遇!
相关文章:

【一百零八】【算法分析与设计】P1908 逆序对,P1637 三元上升子序列,树状数组区间和应用
P1908 逆序对 逆序对 题目描述 猫猫 TOM 和小老鼠 JERRY 最近又较量上了,但是毕竟都是成年人,他们已经不喜欢再玩那种你追我赶的游戏,现在他们喜欢玩统计。 最近,TOM 老猫查阅到一个人类称之为“逆序对”的东西,这东西…...

【RK3568】制作Android11开机动画
Android 开机 logo 分为两种:静态显示和动态显示。静态显示就是循环显示一张图片;动态显示就是以特定帧率顺序显示多张图片 1.准备 android logo 图片 Android logo最好是png格式的,因为同一张图片的情况下,png 格式的比 jpg和b…...

chrony内网同步服务器时间
当前需要在10.26.24.62和10.26.24.61两个服务器上设置chrony同步时间,其中10.26.24.62为NTP时间服务器,10.26.24.61去10.26.24.62同步时间 检查Chrony配置文件: 确认10.26.24.62(NTP服务器)的配置文件 /etc/chrony/c…...

SSM物流管理系统的设计与实现-计算机毕业设计源码44323
摘 要 科技进步的飞速发展引起人们日常生活的巨大变化,电子信息技术的飞速发展使得电子信息技术的各个领域的应用水平得到普及和应用。信息时代的到来已成为不可阻挡的时尚潮流,人类发展的历史正进入一个新时代。在现实运用中,应用软件的工作…...

STM32CubeIDE使用过程记录
最近在做一款机器人的开发,使用到了STM32CubeIDE,这里记录一些使用技巧方便后续查阅。 STM32CubeIDE使用过程记录 快捷键开启代码自动补全功能看门狗设置CRC设置IO口取反定时器设置 及 定时器中断外部中断GPIO配置STC15单片机GPIO模式配置片内闪存&#…...

angular2开发知识点
目录 文章目录 一、API 网关地址 配置二、服务注册使用三、模块组件注册使用四、html中style类动态绑定1. 单个类的绑定:[class.special]"isSpecial"2. 多个类的绑定:[ngClass]"{selected:status ,saveable: this.canSave,}"3. 单个…...

【机器学习】机器学习与智能交通在智慧城市中的融合应用与性能优化新探索
文章目录 引言机器学习与智能交通的基本概念机器学习概述监督学习无监督学习强化学习 智能交通概述交通流量预测交通拥堵管理智能信号控制智能停车管理 机器学习与智能交通的融合应用实时交通数据分析数据预处理特征工程 交通流量预测与优化模型训练模型评估 智能信号控制与优化…...

走的人多了,也便成了路(七)
好多年前就听到这样的说法:一流的企业做标准,二流的企业做品牌,三流的企业做产品。 在通信行业待久了,经历了移动通信技术标准的发展历程,体会到很多事情没有那么神秘,甚至由于一些偶然因素的出现ÿ…...

UE5中在地形中加入湖、河
系统水资产添加 前提步骤123 完成 前提 使用版本 UE5.0.3,使用插件为UE内置的Water和water Extras. 步骤 1 记得重启 2 增加地形,把<启用编辑图层>勾选 如果地形没有勾选上编辑图层,那么就会导致湖、河等水景象无法融入地形。 如果忘记勾选…...

【280个shell脚本】----提示运维工作效率
1.MySQL 数据库备份单循环 #!/bin/bash DATE$(date %F_%H-%M-%S) HOSTlocalhost USERbackup PASS123.com BACKUP_DIR/data/db_backup DB_LIST$(mysql -h$HOST -u$USER -p$PASS -s -e "show databases;" 2>/dev/null |egrep -v "Database|information_schema…...
从零开始搭建Electron项目之运行例程
最好的学习方式就是:给一段能够运行的代码示例。 本文给出了例程资源,以及运行的步骤。 在国内开发electron有一点特别不好,就是如果不爬梯子,下载依赖容易出错。 一、例程资源 到如下路径下载例程到本地。 GitCode - 全球开发者…...

MySQL逻辑备份
目录 一.mysqldump 基本命令: 参数选项: 示例 备份整个数据库 备份多个数据库 备份所有数据库 仅备份数据库结构 仅备份特定表 添加选项以有效处理锁表问题 恢复数据 恢复数据库 恢复库中的表 使用source恢复 注意事项 二. mysqlpu…...

python 获取网页链接图片
python 获取 网页图片 在Python中,可以使用requests库获取网页内容,再使用BeautifulSoup解析网页,提取图片链接,最后保存图片到本地。以下是一个简单的例子: import requests from bs4 import BeautifulSoup import o…...
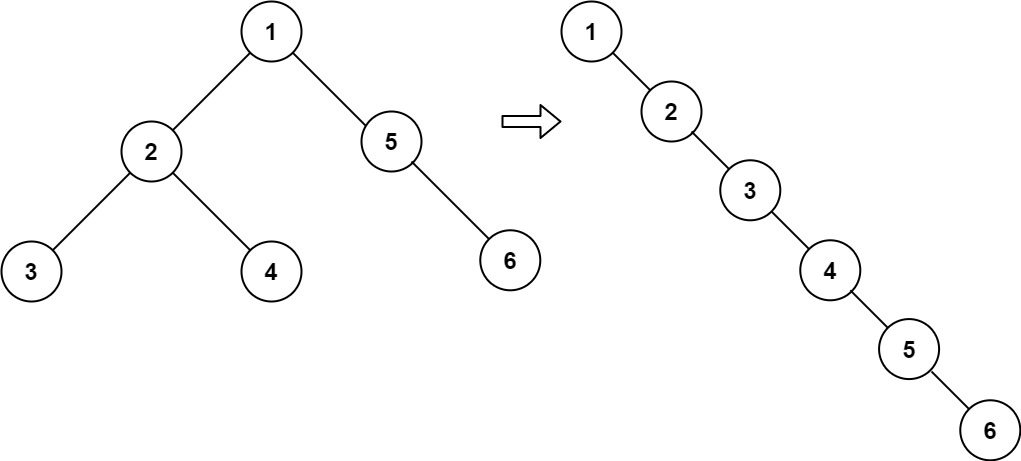
Leetcode 力扣114. 二叉树展开为链表 (抖音号:708231408)
给你二叉树的根结点 root ,请你将它展开为一个单链表: 展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。展开后的单链表应该与二叉树 先序遍历 顺序相同。 示例 1…...
文刻ai工具跟绘唐AI工具有什么区别
文刻AI工具和绘唐AI工具是两种不同的人工智能工具。点击查看 文刻AI工具是一种自然语言处理工具,可以用于生成、修改和校对文本。它可以帮助用户更高效地写作,提供词汇和语法建议,检查拼写和语法错误,并提供自动补全和自动纠正功…...

手写kNN算法的实现-用欧几里德空间来度量距离
kNN的算法思路:找K个离预测点最近的点,然后让它们进行投票决定预测点的类型。 step 1: kNN存储样本点的特征数据和标签数据step 2: 计算预测点到所有样本点的距离,关于这个距离,我们用欧几里德距离来度量(其实还有很多…...
IGraph使用实例——线性代数计算(blas)
1 概述 在图论中,BLAS(Basic Linear Algebra Subprograms)并不直接应用于图论的计算,而是作为一套线性代数计算中通用的基本运算操作函数集合,用于进行向量和矩阵的基本运算。然而,这些基本运算在图论的相…...

【MySQL】(基础篇五) —— 排序检索数据
排序检索数据 本章将讲授如何使用SELECT语句的ORDER BY子句,根据需要排序检索出的数据。 排序数据 还是使用上一节中的例子,查询employees表中的last_name字段 SELECT last_name FROM employees;输出结果: 发现其输出并没有特定的顺序。其实…...

C++ C_style string overview and basic Input funcitons
write in advance 最近在做题,遇到一个简单的将console的输入输出到文件中的简单题目,没有写出来。悔恨当初没有踏实地总结string 相关的 I/O 以及与文件的操作。这篇文章旨在记录基础的字符I/O, 简单常用的文件I/O操作函数。 当然,你会说C…...

VS2022+Qt雕刻机单片机马达串口上位机控制系统
程序示例精选 VS2022Qt雕刻机单片机马达串口上位机控制系统 如需安装运行环境或远程调试,见文章底部个人QQ名片,由专业技术人员远程协助! 前言 这篇博客针对《VS2022Qt雕刻机单片机马达串口上位机控制系统》编写代码,代码整洁&a…...

测试微信模版消息推送
进入“开发接口管理”--“公众平台测试账号”,无需申请公众账号、可在测试账号中体验并测试微信公众平台所有高级接口。 获取access_token: 自定义模版消息: 关注测试号:扫二维码关注测试号。 发送模版消息: import requests da…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Lombok 的 @Data 注解失效,未生成 getter/setter 方法引发的HTTP 406 错误
HTTP 状态码 406 (Not Acceptable) 和 500 (Internal Server Error) 是两类完全不同的错误,它们的含义、原因和解决方法都有显著区别。以下是详细对比: 1. HTTP 406 (Not Acceptable) 含义: 客户端请求的内容类型与服务器支持的内容类型不匹…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程,系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
