备战 清华大学 上机编程考试-冲刺前50%,倒数第5天
T1:多项式求和
小K最近刚刚习得了一种非常酷炫的多项式求和技巧,可以对某几类特殊的多项式进行运算。非常不幸的是,小K发现老师在布置作业时抄错了数据,导致一道题并不能用刚学的方法来解,于是希望你能帮忙写一个程序跑一跑。给出一个 \(m\) 阶多项式\(\(f(x)=\sum_{i=0}^mb_ix^i\)\)对给定的正整数 \(a\) ,求\(\(S(n)=\sum_{k=0}^na^kf(k)\)\)由于这个数可能比较大,所以你只需计算 \(S(n)\) 对 \(10^9+7\) 取模后的值(即计算除以 \(10^9+7\) 后的余数)。


解:
涉及到:a*b整数相乘的优化, a^n的优化,
多项式的计算-一个for循环,
自然数的幂次求和公式-数学推导
#include<iostream>
#include<vector>
#include<algorithm>
#include<string>
#include<stdio.h>
#include<stdlib.h>using namespace std;
//计算多项式的值的题目://“轩轩”前辈的代码非常值得学习,故而尝试 自己 默记着 尝试复写long long int n,m,a;
long long int mod = 1e9+7;
long long int *b; //作为数组,之后可以开辟空间//处理输入的函数:
void init_input()
{//给上述变量赋值 和 处理b0 - bncin>>n>>m>>a;b = new long long int[m+1];for(int i = 0 ;i<=m ;i++){cin>>b[i];}
}//处理 (a*b)%mod 的快速算法:
long long multiply(long long a,long long b , long long mod)
{long long ans = 0;//我觉得这里还可以优化:让b是那个小的数if(b > a){long long tmp = b;b = a;a = tmp;}while(b > 0){if(b&1 != 0){//b是一个奇数:ans = (ans + a)%mod;}a = (a<<1 ) % mod;b = b>>1;}return ans;
}//处理 a^n次方的 快速算法:
long long power(long long a, long long n , long long mod)
{long long ans = 1 ;//计算a的n次方:while(n > 0 ){if(n&1 != 0){//奇数:ans = multiply(ans,a,mod);}n = n>>1;ans = multiply(ans,ans,mod);}return ans;
}//计算 f(k) 的结果:
long long func(long long x)
{long long ans = 0;//而且,我觉得可以改进一点, 求x的i次方,可以用到x的i-1次方long long tmp = 1;for(long long i = 0 ; i<=m ;i++){ans = (ans + multiply(tmp,b[i],mod))%mod;tmp = multiply(tmp,x,mod) % mod ; }return ans;
}//最后,计算S(n)的求和结果
long long Sum()
{long long ans = 0;//改进:保留 a的k-1次方的结果:long long tmp = 1;for(long long i = 0 ; i<=n ;i++){ans = (ans + multiply(func(i),tmp,mod))%mod;tmp = (multiply(tmp,a,mod))%mod;}return ans;
}int main()
{//处理输入:// int n,m,a;// cin>>n>>m>>a;// vector<int> vec(m+1,0);// for(int i= 0; i<= m; i++)// {// cin>>vec[i];// }//朴素一点的方法进行计算——先做一个垃圾出来://第一步:需要一个计算f(k) % mod//第二步:再计算S(n)//可以改进的地方://1.(a*b)%mod 可以利用 2的幂次 以及 左移,右移优化//2.计算a^k次方, 可以利用 2的幂次进行优化//其他的话,暂时就只能那样子了init_input();cout<<Sum()<<endl;//虽然,样例9 和 样例10 我肯定是做不出来的,//但是,只要过了一些样例,就有分,为啥不干脆 “针对样例编程”?//要有针对性! -- 得分为王//第一:针对 a = 1的情况, —— 只要算f(k)求和即可//这里一定有更加高效的计算-可以合并 - 分治等//目前我的想法只有合并:if(a == 1){//但是如果要开辟一个10^9次方的数组的话,开辟不了//nice,合并之后,感觉因为m很小,复杂度可以降低到O(n)//甚至,只要知道1次求和,2次求和,3次求和,4次求和公式。。。。妙!//参考:https://www.bilibili.com/read/cv11243219///这个问题就是 “自然数”幂等和问题://根据这个参考文章,基本就可以搞定所有a=1的case了//数学的美妙就在其中,而清华,必然是招收能够体会数学之美的学生//这里以m=2 , a =1 那个测试用例进行写代码:if(a == 1 && m==2){ //别忘了 0 的 0次方是 1long long sum = (b[0]*(n+1) %mod+b[1]*(n*(n+1)/2)%mod+ b[2]*(n*(n+1)*(2*n+1)/6)%mod)%mod;cout<<sum<<endl;}}return 0 ;
}
T2:葱的战争--模拟题
一个n乘m的棋盘,上面有k根葱,每根葱面朝方向为d(0123分别表示上下左右),没跟葱一个战斗力f。每隔时间葱会向面朝方向走一格,如果遇到棋盘边界,那么他将把面朝方向转180度(此回合葱不会走动),如果某个时刻有两个或以上的葱在同一位置,那么他们将发生战争,只有战斗力最高的葱存活,其他的葱全部原地枯萎,不在走动,求经过t时间后所有葱的位置
输入:第一行n m k,然后接下来k行每根葱的信息x y d f(坐标,方向,战斗力),最后一行输入时间t 输出:k行,分别表示每个葱的位置。 数据范围:n和m在100内,k在1000内,t在1000内,f在1000内,保证初始每颗葱位置不同,战斗力不同。
解:
结合之前的开发经验,这一题和 “贪吃蛇”的项目基本类似:
直接使用 模拟的思想,——关键是记录 board[][]和 snake里面的数据:
测试用例:
输入:
5 4 2
1 1 3 10
3 1 2 5
3
输出:
4 1
2 1#include<iostream>
#include<string>
#include<vector>
#include<stdio.h>
#include<stdlib.h>using namespace std;struct cong
{int x;int y;int d;int f;//尝试写一个默认构造函数:cong(){this->x =0;this->y =0; this->d =0;this->f =0;}
};int n,m,k;
int t;//算了,如果是二维数组的话,我还是老老实实的用int a[100][100]
//或者vector<vector<int> > vec(n,vector<int>(m,0))这种int main()
{//这个就是一个简单的 模拟题目 搞定即可://最关键一个点可能就是 数据如何存储的问题//处理输入 和 存储结构cin>>n>>m>>k;cong arr[1001];int flag[1001]; //用于记录这根是否存活,只有flag==0时,才需要更新//cong的下标是从1开始用的for(int i = 1;i <=k ;i++) //arr从1开始用!!!cong的下标{cin>>arr[i].x>>arr[i].y>>arr[i].d>>arr[i].f;}cin>>t;//直接模拟t个时间-for循环-立即更新board数据 和 arr数据for(int i=1;i <=t ;i++){//这里,设置一个board二维矩阵,nxm位置初始为0//之后,每次更新一个 活着的cong,在更新后的那里写上cong的下标//如果原来那个位置有非0的下标——>战斗->f小的那个flag设置为1,//坐标范围(0-n-1,0-m-1)//到达边界,下一个回合进行扭转,扭转也算做一步int board[101][101]; // 下标从0开始用,我估计是//调用for(int j = 1; j<=k;j++){if(flag[j] != 0){continue; //这根cong已经 不活了}//--否则进行更新://上:if(arr[j].d == 0){//是否到达上边界:if(arr[j].y == m-1) //我就按照正常的笛卡尔坐标来!之前那个贪吃蛇有点不同{//修改arr[j].d即可arr[j].d = 1;//--判断board同一个位置是否需要战斗if(board[arr[j].x][arr[j].y] != 0 ){//战斗:int index = board[arr[j].x][arr[j].y];if(arr[j].f > arr[index].f){// j留下board[arr[j].x][arr[j].y] = j;flag[index] = 1;}else{// index留下flag[j] = 1;//阵亡}}else{//在board上面占一个坑位,等其他人过来board[arr[j].x][arr[j].y] = j;}}else{//向上移动1格:arr[j].y +=1;//--判断board同一个位置是否需要战斗if(board[arr[j].x][arr[j].y] != 0 ){//战斗:int index = board[arr[j].x][arr[j].y];if(arr[j].f > arr[index].f){// j留下board[arr[j].x][arr[j].y] = j;flag[index] = 1;}else{// index留下flag[j] = 1;//阵亡}} else{//在board上面占一个坑位,等其他人过来board[arr[j].x][arr[j].y] = j;}}}//下:else if(arr[j].d == 1){//是否到达下边界:if(arr[j].y == 0) //我就按照正常的笛卡尔坐标来!之前那个贪吃蛇有点不同{//修改arr[j].d即可arr[j].d = 0;//--判断board同一个位置是否需要战斗if(board[arr[j].x][arr[j].y] != 0 ){//战斗:int index = board[arr[j].x][arr[j].y];if(arr[j].f > arr[index].f){// j留下board[arr[j].x][arr[j].y] = j;flag[index] = 1;}else{// index留下flag[j] = 1;//阵亡}}else{//在board上面占一个坑位,等其他人过来board[arr[j].x][arr[j].y] = j;}}else{//向下移动1格:arr[j].y -=1;//--判断board同一个位置是否需要战斗if(board[arr[j].x][arr[j].y] != 0 ){//战斗:int index = board[arr[j].x][arr[j].y];if(arr[j].f > arr[index].f){// j留下board[arr[j].x][arr[j].y] = j;flag[index] = 1;}else{// index留下flag[j] = 1;//阵亡}} else{//在board上面占一个坑位,等其他人过来board[arr[j].x][arr[j].y] = j;}}}//左:else if(arr[j].d == 2){//是否到达上边界:if(arr[j].x == 0) //我就按照正常的笛卡尔坐标来!之前那个贪吃蛇有点不同{//修改arr[j].d即可arr[j].d = 3;//--判断board同一个位置是否需要战斗if(board[arr[j].x][arr[j].y] != 0 ){//战斗:int index = board[arr[j].x][arr[j].y];if(arr[j].f > arr[index].f){// j留下board[arr[j].x][arr[j].y] = j;flag[index] = 1;}else{// index留下flag[j] = 1;//阵亡}}else{//在board上面占一个坑位,等其他人过来board[arr[j].x][arr[j].y] = j;}}else{//向左移动1格:arr[j].x -=1;//--判断board同一个位置是否需要战斗if(board[arr[j].x][arr[j].y] != 0 ){//战斗:int index = board[arr[j].x][arr[j].y];if(arr[j].f > arr[index].f){// j留下board[arr[j].x][arr[j].y] = j;flag[index] = 1;}else{// index留下flag[j] = 1;//阵亡}} else{//在board上面占一个坑位,等其他人过来board[arr[j].x][arr[j].y] = j;}}}//右:else if(arr[j].d == 3){//是否到达上边界:if(arr[j].x == n-1) //我就按照正常的笛卡尔坐标来!之前那个贪吃蛇有点不同{//修改arr[j].d即可arr[j].d = 2;//--判断board同一个位置是否需要战斗if(board[arr[j].x][arr[j].y] != 0 ){//战斗:int index = board[arr[j].x][arr[j].y];if(arr[j].f > arr[index].f){// j留下board[arr[j].x][arr[j].y] = j;flag[index] = 1;}else{// index留下flag[j] = 1;//阵亡}}else{//在board上面占一个坑位,等其他人过来board[arr[j].x][arr[j].y] = j;}}else{//向右移动1格:arr[j].x +=1;//--判断board同一个位置是否需要战斗if(board[arr[j].x][arr[j].y] != 0 ){//战斗:int index = board[arr[j].x][arr[j].y];if(arr[j].f > arr[index].f){// j留下board[arr[j].x][arr[j].y] = j;flag[index] = 1;}else{// index留下flag[j] = 1;//阵亡}} else{//在board上面占一个坑位,等其他人过来board[arr[j].x][arr[j].y] = j;}}}}}//输出k行,也就是最后的k根cong的位置for(int i =1 ;i<=k ;i++){cout<<arr[i].x<<" "<<arr[i].y<<endl;}return 0;
}T3:路径个数
有n个点,每个点有一个权值,每两点间的不同边的个数为他们权值相与得到的值的二进制数字中的1的个数(边为有向边,有第i指向第j,i小于j)求第1个点到第n个点的路径个数(当且仅当不止一条边不同才被称为两条不同的路径),由于数据很大,对991247取模。
输入:第1行n,第二行分别试每个点权值 输出:路径个数 数据范围:n在2e5内,权值大小在1e9内
解:
(1)补充:<bitset>库中的使用示例:
#include <iostream>
#include <bitset>int main() {// 定义一个包含8位的bitset,初始化所有位为0std::bitset<8> bitset1;// 通过下标赋值bitset1[0] = 1; // 设置第一位为1bitset1[3] = 1; // 设置第四位为1// 输出bitsetstd::cout << "Bitset1: " << bitset1 << std::endl; // 输出可能是 "00010010"// 通过整数初始化std::bitset<8> bitset2(7); // 二进制表示为 00000111std::cout << "Bitset2: " << bitset2 << std::endl; // 输出 "00000111"// 通过字符串初始化std::bitset<8> bitset3("10101010");std::cout << "Bitset3: " << bitset3 << std::endl; // 输出 "10101010"// 访问和修改std::cout << "Third bit of bitset3: " << bitset3.test(2) << std::endl; // 输出1,因为第三位是1bitset3.flip(2); // 翻转第三位std::cout << "After flipping third bit: " << bitset3 << std::endl; // 输出可能是 "10101000"// 操作std::bitset<8> bitset4("11110000");std::cout << "Bitset4 & bitset2: " << (bitset4 & bitset2) << std::endl; // 位与操作std::cout << "Bitset4 | bitset2: " << (bitset4 | bitset2) << std::endl; // 位或操作std::cout << "Bitset4 ^ bitset2: " << (bitset4 ^ bitset2) << std::endl; // 位异或操作return 0;
}(2)更正参考解法:
//路径:
#include<iostream>
#include<algorithm>
#include<vector>
#include<string>
#include<stdio.h>
#include<stdlib.h>using namespace std;//不要想那么多,置之死地而后生,对得起自己的money和精力即可,结果不要管他
//成为一个正在的编程算法强者,用思考力证明自己,这东西到哪都很有用!
//这一题很有意思,关键当然是 如何计算 “权值 与运算 后,二进制1的个数”
vector<int> power;
int n;void init()
{cin>>n;for(int i = 0;i<n ;i++){int tmp;cin>>tmp;power.push_back(tmp);}
}//写一个函数:输入2个整数, 输出 计算出1的个数:
//注意:调用bitset库 和 不调用库实现:
int count1(int a,int b)
{int ans = 0 ;int tmp = a&b;while(tmp>0){if(tmp&1 !=0) // 或者 tmp%2 == 1{ans++;}tmp = tmp>>1;}return ans;}//第二个关键点:让我想起了 罗文寒 的那个 5=1+1+1+1+1的个数那个,递归思想//这一题我不太能接受,我给一个测试用例吧,如果对了还好,不对就自己再想一个:
//果然,就是有问题 —— 估计是题目给错了,不过,那我不如将错就错的写一写
int calc(int n )
{if(n == 1){return 2;}else{return 2+calc(n-1)*2;}
}//我的解法的测试用例:其中i与j之间都是2条路:
int calc2(int i , int j)
{if( i == j ){return 1;}else{int ans = 0;for(int k = i+1; k<=j ;k++){ans =(ans + 2*calc2(k,j))%991127;}return ans;}
}//下面这个是作为 该题答案
int mycalc(int i , int j)
{//i是小的那个起点 , j是大的那个终点://递归出口:if( i == j){return 1;}else{int ans = 0;for(int k = i+1; k<=j ;k++){ans =(ans + count1(power[i],power[k])*mycalc(power[k],power[j]))%991127;}return ans;}}int main()
{cout<<calc(3)<<endl; //输出14 -不对cout<<calc2(0,3)<<endl; //输出18 -这才对return 0;
}
相关文章:

备战 清华大学 上机编程考试-冲刺前50%,倒数第5天
T1:多项式求和 小K最近刚刚习得了一种非常酷炫的多项式求和技巧,可以对某几类特殊的多项式进行运算。非常不幸的是,小K发现老师在布置作业时抄错了数据,导致一道题并不能用刚学的方法来解,于是希望你能帮忙写一个程序…...

leetCode127. 单词接龙
leetCode127. 单词接龙 // bfs 剪枝 class Solution { public:int ladderLength(string beginWord, string endWord, vector<string>& wordList) {// 1.将所有的单词放在set字段中unordered_set<string> s;for (auto & ele : wordList) s.insert(ele);//…...

进程概念(二)
目录 进程优先级基本概念查看系统进程PRI and NIPRI vs NI修改进程优先级的命令renice修改优先级进程其他概念 环境变量基本概念查看环境变量方法常见环境变量PATHHOMESHELL 查看环境变量环境变量相关的命令 环境变量特征命令行参数main函数中的俩个参数 argc argvmain函数的第…...

java程序100道01—20
1.用循环的嵌套,输出输出如下图形 * * * * * * * * * * * * * * * * * * * * * * * * * package Exercises.One_Hundred; public class Demo01 {public static void main(String[] args) {for(int i1;i<5;i){for(int j1;j<2*i-1;j){Sys…...

让GNSSRTK不再难【第二天-第7部分2】
状态更新计算过程: 计算卡尔曼增益: 根据预测的误差协方差矩阵 P k − P_k^- Pk− 和观测噪声协方差矩阵 R R R 计算卡尔曼增益 K k K_k Kk: K k P k − H T ( H P k − H T R ) − 1 K_k P_k^- H^T (H P_k^- H^T R)^{-1} KkPk…...

计算引擎:Flink核心概念
Apache Flink 是一个流处理框架,擅长处理实时数据流和批处理任务。Flink 提供了强大的功能来处理和分析大量数据。以下是 Flink 的核心概念: 1. DataStream 和 DataSet API DataStream API: 用于处理无界数据流,即不断生成和流动的数据。例如,传感器数据、日志等。DataSet…...
技术前沿 |【大模型InstructBLIP进行指令微调】
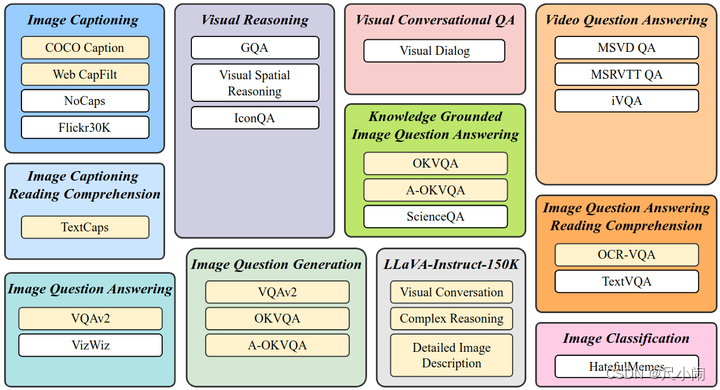
大模型InstructBLIP进行指令微调 一、引言二、InstructBLIP模型介绍三、指令微调训练通用视觉语言模型的应用潜力四、InstructBLIP的指令微调训练步骤五、实验结果与讨论六、结论与展望 一、引言 随着人工智能技术的快速发展,视觉语言模型(Vision-Langu…...

CSS-布局-flex
CSS3 新增了弹性盒子模型( Flexible Box 或 FlexBox ),是一种新的用于在 HTML 页面实现布局的方式。使得 HTML 页面适应不同尺寸的屏幕和不同的设备时,元素是可预测地运行。 基本概念 容器:使用 display:flex 或 display:inline-flex 声明的…...

「C系列」C 数组
文章目录 一、C 数组1. 声明数组2. 初始化数组3. 访问数组元素4. 数组越界5. 多维数组 二、C 操作数组的方法有哪些三、C 数组-应用场景1. 存储固定数量的数据2. 实现算法(如排序)3. 处理数据集合 四、相关链接 一、C 数组 在C语言中,数组是…...

Python框架scrapy有什么天赋异禀
Scrapy框架与一般的爬虫代码之间有几个显著的区别,这些差异主要体现在设计模式、代码结构、执行效率以及可扩展性等方面。下面是一些关键的不同点: 结构化与模块化: Scrapy:提供了高度结构化的框架,包括定义好的Spider…...

【ROS2大白话】四、ROS2非常简单的传参方式
系列文章目录 【ROS2大白话】一、ROS2 humble及cartorgrapher安装 【ROS2大白话】二、turtlebot3安装 【ROS2大白话】三、给turtlebot3安装realsense深度相机 【ROS2大白话】四、ROS2非常简单的传参方式 文章目录 系列文章目录前言一、launch文件传参的demo1. 编写launch.py文…...

浅谈mysql 的批量delete 和 使用in条件批量删除问题
在考虑这两个DELETE语句的性能时,我们需要考虑数据库如何执行这些查询以及它们背后可能涉及的索引和数据结构。 1.执行多个单独的DELETE语句: DELETE FROM a WHERE b 1 AND c 1; ... DELETE FROM a WHERE b 1000 AND c 1000; 这种方法的优点是每…...

【Spring Boot】过滤敏感词的两种实现
文章目录 项目场景前置知识前缀树 实现方式解决方案一:读取敏感词文件生成前缀树构建敏感词过滤器1. 导入敏感词文件 src/main/resources/sensitive_words.txt2. 构建敏感词过滤器 SensitiveFilter3. 测试与使用 解决方案二:使用第三方插件 houbb/sensit…...
吗)
在 Zustand 中管理状态能使用类(Class)吗
在 Zustand 中,通常不推荐使用类(Class)来管理状态,因为 Zustand 的设计理念是基于函数式编程和 React Hooks 的。然而,仍然可以在 Zustand 中间接地使用类,但这并不是 Zustand 的典型用法。 如果确实想要…...

MoreTable 方法selectWithFun,count 使用实例
ORM Bee, example for MoreTable methods:selectWithFun,count ORM Bee时, MoreTable 方法selectWithFun,count 使用实例 package org.teasoft.exam.bee.osql;import org.teasoft.bee.osql.BeeException; import org.teasoft.bee.osql.FunctionType; import org.teasoft.be…...

【SpringBoot】在Spring中使用自定义条件类在Java声明Bean时实现条件注入
在Spring框架中,通过实现org.springframework.context.annotation.Condition接口并重写matches()方法,可以根据自定义条件来控制Bean的注入。这种机制非常灵活,可以帮助开发人员根据环境或配置来有选择地启用或禁用某些Bean。本文将详细介绍如…...

网卡聚合链路配置
创建名为mybond0的绑定,使用示例如下: # nmcli con add type bond con-name mybond0 ifname mybond0 mode active-backup添加从属接口,使用示例如下: # nmcli con add type bond-slave ifname enp3s0 master mybond0要添加其他从…...
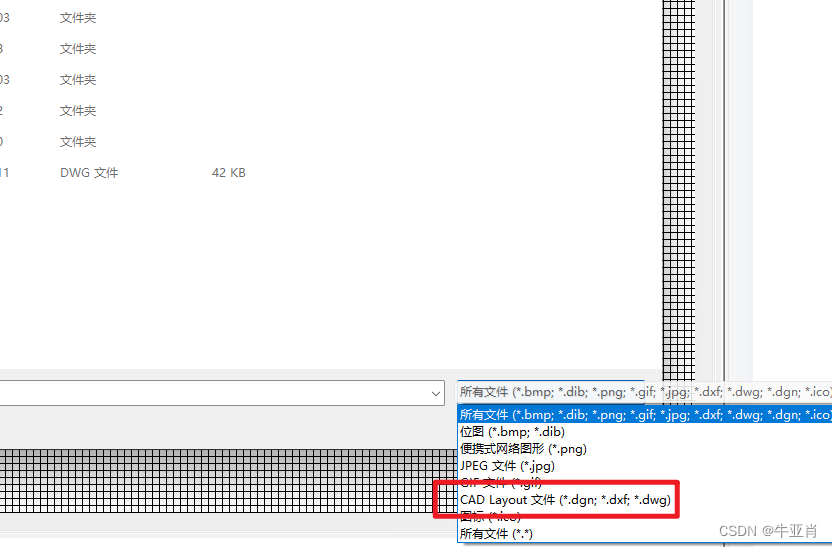
PlantSimulation导入cad图作为背景
PlantSimulation导入cad图作为背景 首先要整理cad文件,正常的工艺规划总图中存在较多杂乱文件,这些信息是不需要的,如果直接导入,会非常卡。 1、打开cad软件,使用layon命令打开所有的隐藏图层,删除不需要…...

【大模型】个人对大模型选择的见解
选择大模型产品时,需要考虑多个因素,包括但不限于以下几点: 需求匹配度:首先,要明确你的需求是什么。不同的大模型产品可能在功能、性能、应用场景等方面有所侧重。例如,有的模型擅长自然语言处理ÿ…...

java的反射和python的鸭子类型
Java的反射(Reflection)和Python的鸭子类型(Duck Typing)感觉相似但又说不出具体的细节,本文借助kimi试图给出总结。 相似之处: 动态性:Java的反射允许程序在运行时查询、创建和修改类和对象的…...

iOS 26 携众系统重磅更新,但“苹果智能”仍与国行无缘
美国西海岸的夏天,再次被苹果点燃。一年一度的全球开发者大会 WWDC25 如期而至,这不仅是开发者的盛宴,更是全球数亿苹果用户翘首以盼的科技春晚。今年,苹果依旧为我们带来了全家桶式的系统更新,包括 iOS 26、iPadOS 26…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...
