当前位置： 首页 > news >正文

为什么说网络安全是风口行业？

news 2026/2/7 21:09:18

前言

“没有网络安全就没有国家安全”。当前，网络安全已被提升到国家战略的高度，成为影响国家安全、社会稳定至关重要的因素之一。

网络安全行业特点

1、就业薪资非常高，涨薪快 2021年猎聘网发布网络安全行业就业薪资行业最高人均33.77万！
2、人才缺口大，就业机会多

2019年9月18日《中华人民共和国中央人民政府》官方网站发表：我国网络空间安全人才 需求140万人，而全国各大学校每年培养的人员不到1.5W人。猎聘网《2021年上半年网络安全报告》预测2027年网安人才需求300W，现在从事网络安全行业的从业人员只有10W人。

行业发展空间大，岗位非常多

网络安全行业产业以来，随即新增加了几十个网络安全行业岗位︰网络安全专家、网络安全分析师、安全咨询师、网络安全工程师、安全架构师、安全运维工程师、渗透工程师、信息安全管理员、数据安全工程师、网络安全运营工程师、网络安全应急响应工程师、数据鉴定师、网络安全产品经理、网络安全服务工程师、网络安全培训师、网络安全审计员、威胁情报分析工程师、灾难恢复专业人员、实战攻防专业人员…

职业增值潜力大

网络安全专业具有很强的技术特性，尤其是掌握工作中的核心网络架构、安全技术，在职业发展上具有不可替代的竞争优势。

随着个人能力的不断提升，所从事工作的职业价值也会随着自身经验的丰富以及项目运作的成熟，升值空间一路看涨，这也是为什么受大家欢迎的主要原因。

从某种程度来讲，在网络安全领域，跟医生职业一样，越老越吃香，因为技术愈加成熟，自然工作会受到重视，升职加薪则是水到渠成之事。

如何入门学习网络安全

零基础入门

对于从来没有接触过网络安全的同学，我们帮你准备了详细的学习成长路线图。可以说是最科学最系统的学习路线，大家跟着这个大的方向学习准没问题。

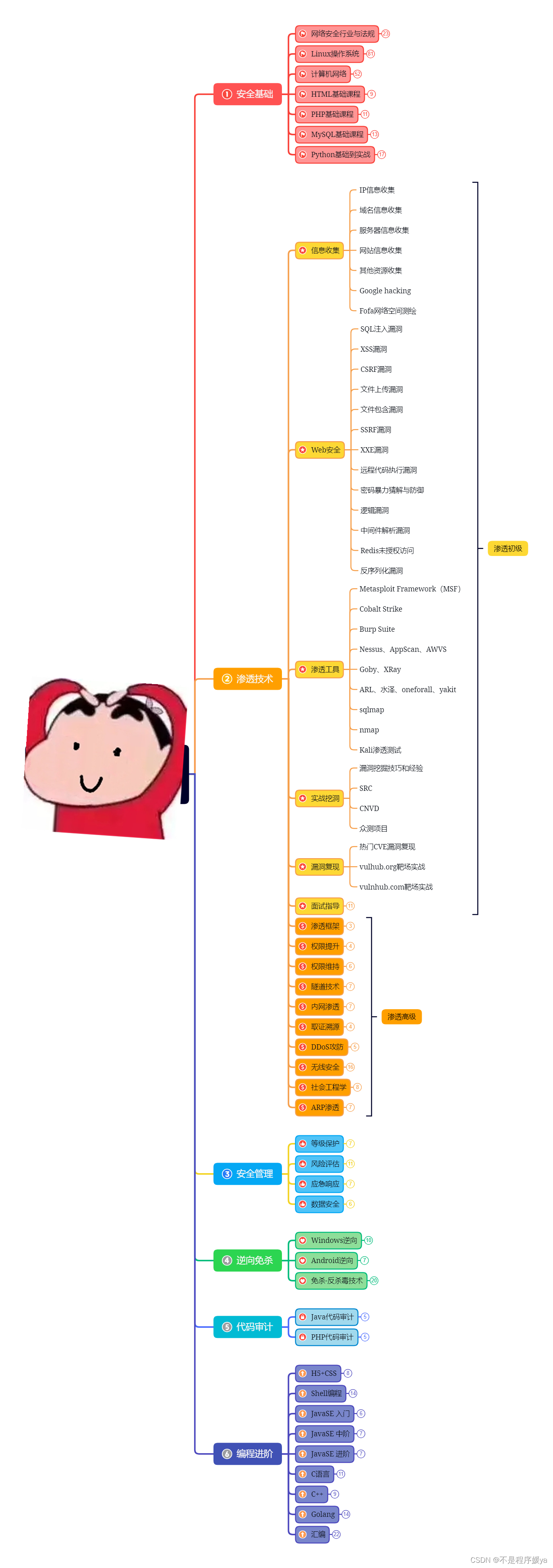
同时每个成长路线对应的板块都有配套的视频提供：

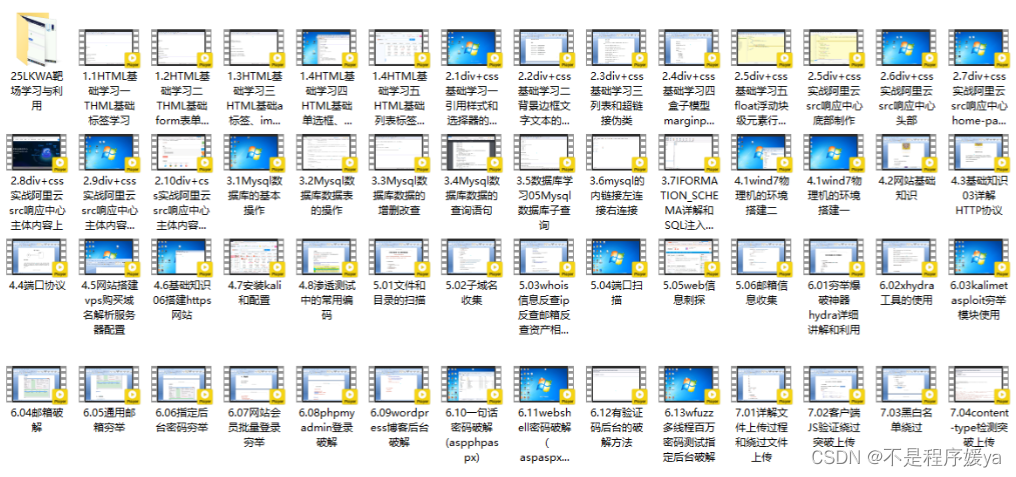
因篇幅有限，仅展示部分 

 

 

 

相关文章：

为什么说网络安全是风口行业？

前言 “没有网络安全就没有国家安全”。当前，网络安全已被提升到国家战略的高度，成为影响国家安全、社会稳定至关重要的因素之一。 网络安全行业特点 1、就业薪资非常高，涨薪快 2021年猎聘网发布网络安全行业就业薪资行业最高人均33.77万&…...

编程日记 2023/2/12 19:46:22

12-PHP使用过的函数 111-120

111、rowCount if ($stmt->execute($data)) {//true//读:select//写:insert,update,delete,成功后会返回表中受影响的记录数量//!rowCount() 返回受影响的记录数量if ($stmt->rowCount() > 0) {echo 新增成功,id . $db->lastInsertId() . <hr>;} else {//…...

编程日记 2023/2/12 19:45:16

【JavaWeb项目】简单搭建一个前端的博客系统

博客系统项目 本项目主要分成四个页面: 博客列表页博客详情页登录页面博客编辑页 该系统公共的CSS样式 common.css /* 放置一些各个页面都会用到的公共样式 */* {margin: 0;padding: 0;box-sizing: 0; }/* 给整个页面加上背景 */ html, body{height: 100%; }body {backgrou…...

编程日记 2023/2/12 19:43:59

iPerf3 -M参数详解，场景分析

本文目录iPerf3 -M参数说明几个典型测试场景中应该如何设定合适的-M参数值理想局域网模型&#xff08;无丢包&#xff0c;无抖动&#xff09;高丢包&#xff0c;无抖动模型高丢包&#xff0c;高抖动模型&#xff08;网络质量比较差&#xff0c;IP转发路径变化频繁&#xff09;总…...

编程日记 2023/2/12 19:42:53

java的基本语法以及注意事项

Java 基础语法一个 Java 程序可以认为是一系列对象的集合&#xff0c;而这些对象通过调用彼此的方法来协同工作。下面简要介绍下类、对象、方法和实例变量的概念。对象&#xff1a;对象是类的一个实例&#xff0c;有状态和行为。例如&#xff0c;一条狗是一个对象&#xff0c;它…...

编程日记 2023/2/12 19:41:41

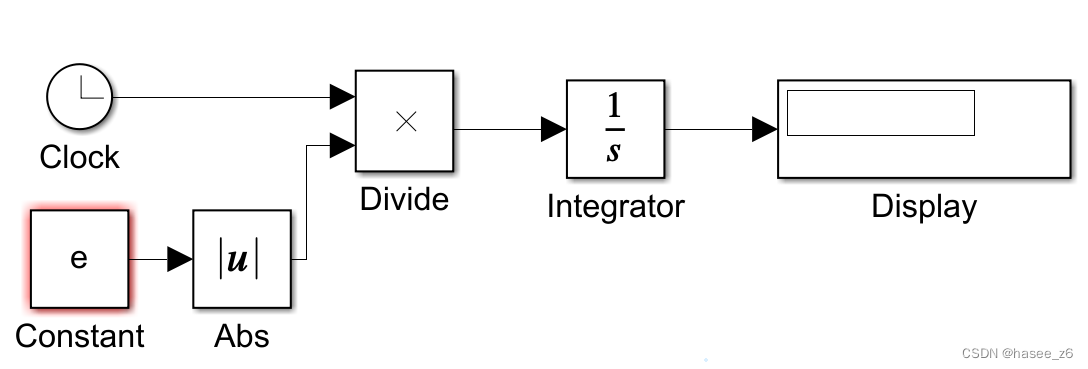
matlab搭建IAE，ISE，ITAE性能指标

目录前言准备IAEISEITAE前言 最近在使用matlab搭建控制系统性能评价指标模型&#xff0c;记录一下 准备 MATLAB R2020 IAE IAE函数表达式如下所示&#xff1a; IAE函数模型如下所示&#xff1a; ISE ISE函数表达式如下所示&#xff1a; ISE函数模型如下所示&#xff…...

编程日记 2023/2/12 19:40:36

docker安装mysql

在安装Mysql之前&#xff0c;我们可以先查看一下我们的镜像&#xff0c;输入命令&#xff1a; docker images 能发现&#xff0c;镜像里面只有一个Nginx&#xff0c;并没有Mysql 然后我们可以像上一篇安装Nginx一样&#xff0c;安装Mysql镜像。 输入以下命令&#xff0c;安装…...

编程日记 2023/2/12 19:39:28

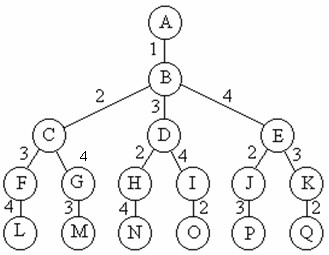
Leetcode 回溯详解

回溯法 回溯法有“通用解题法”之称&#xff0c;用它可以系统地搜索问题的所有解。回溯法是一个既带有系统性又带有跳跃性的搜索算法。 在包含问题的所有解的解空间树中&#xff0c;按照深度优先搜索(DFS)&#xff09;的策略&#xff0c;从根结点出发深度探索解空间树。当探索…...

编程日记 2023/2/12 19:38:19

AI_Papers：第一期

2023.02.06—2023.02.12 文摘词云 Top Papers Subjects: cs.CL 1.Multimodal Chain-of-Thought Reasoning in Language Models 标题&#xff1a;语言模型中的多模式思维链推理 作者&#xff1a;Zhuosheng Zhang, Aston Zhang, Mu Li, Hai Zhao, George Karypis, Alex Sm…...

编程日记 2023/2/12 19:37:13

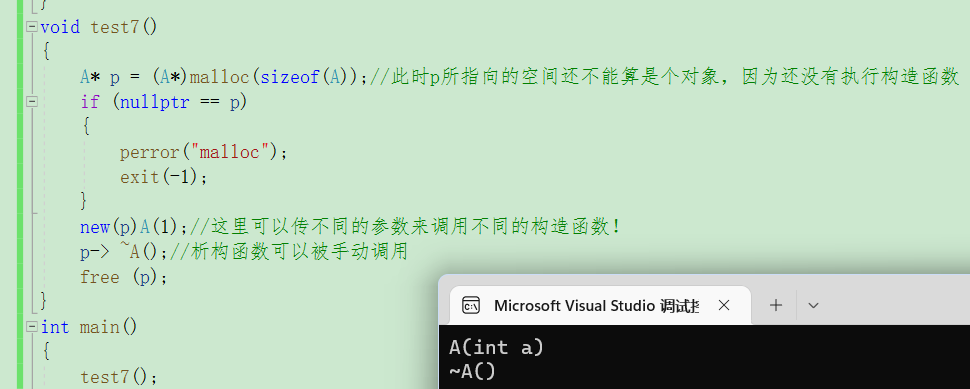
C/C++内存管理

C/C内存管理C/C内存分布C语言中内存管理的方式&#xff1a;malloc/calloc/realloc/freeC内存管理方式内置类型自定义类型operator new 与operator deletenew和delete的实现原理内置类型自定义类型定位new表达式(placement-new)new/delete与malloc/free的区别C/C内存分布 我们先…...

编程日记 2023/2/12 19:36:06

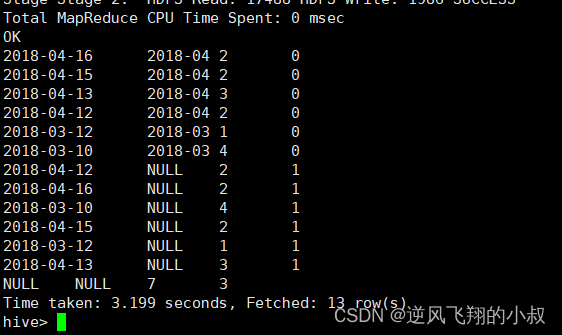
【大数据hive】hive 函数使用详解

一、前言 在任何一种编程语言中&#xff0c;函数可以说是必不可少的&#xff0c;像mysql、oracle中&#xff0c;提供了很多内置函数&#xff0c;或者通过自定义函数的方式进行定制化使用&#xff0c;而hive作为一门数据分析软件&#xff0c;随着版本的不断更新迭代&#xff0c…...

编程日记 2023/2/12 19:34:58

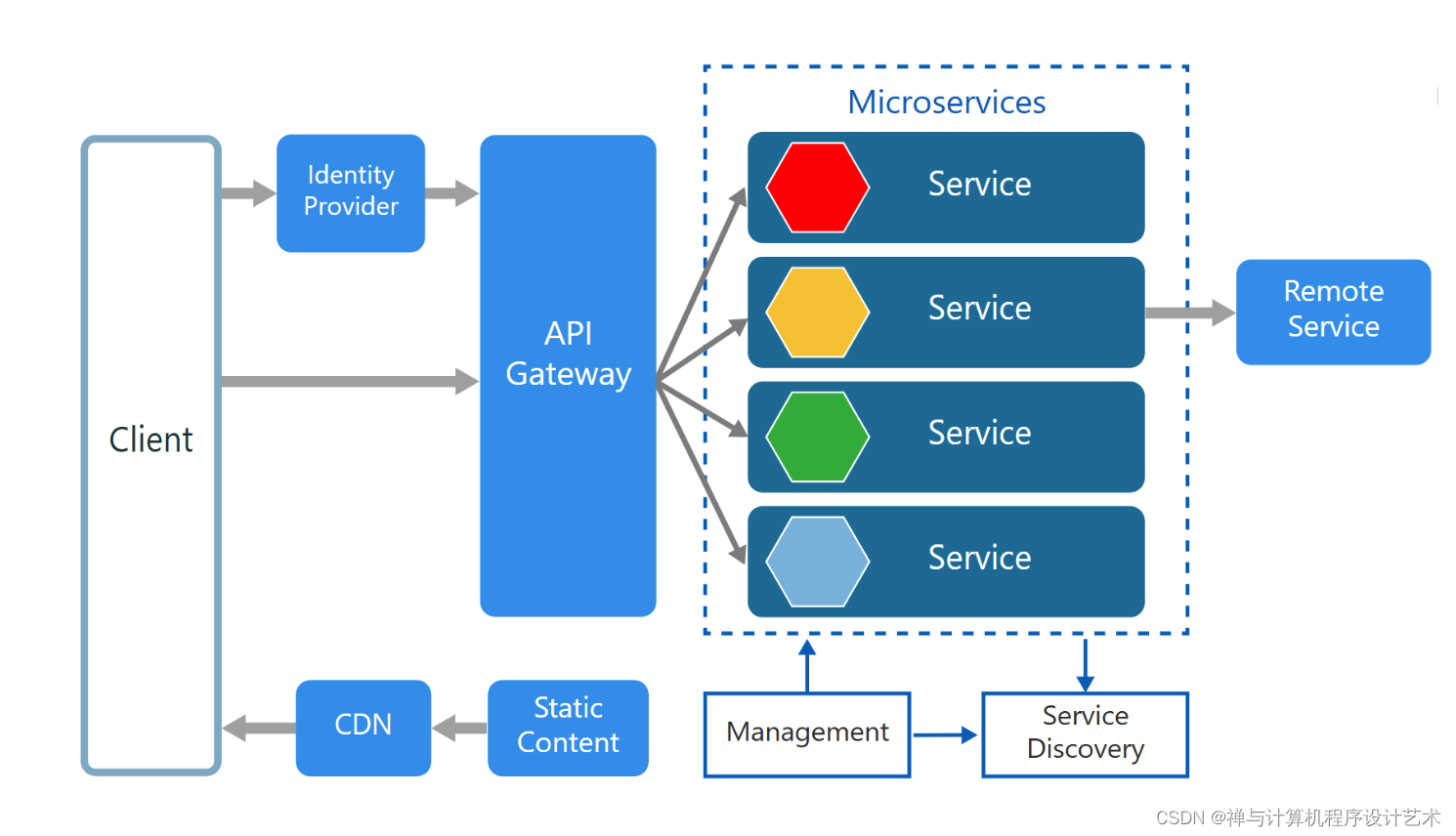
彻底搞懂分布式系统服务注册与发现原理

目录 引入服务注册与发现组件的原因 单体架构 应用与数据分离...

编程日记 2023/2/12 19:32:47

安卓Camera2用ImageReader获取NV21源码分析

以前如何得到Camera预览流回调 可以通过如下方法&#xff0c;得到一路预览回调流 Camera#setPreviewCallbackWithBuffer(Camera.PreviewCallback)&#xff0c;可以通过如下方法&#xff0c;设置回调数据的格式&#xff0c;比如 ImageFormat.NV21 Camera.Parameters#setPreview…...

编程日记 2023/2/12 19:31:39

24. 两两交换链表中的节点

文章目录题目描述迭代法递归法参考文献题目描述 给你一个链表&#xff0c;两两交换其中相邻的节点&#xff0c;并返回交换后链表的头节点。你必须在不修改节点内部的值的情况下完成本题&#xff08;即&#xff0c;只能进行节点交换&#xff09;。 示例 1&#xff1a; 输入&a…...

编程日记 2023/2/12 19:30:30

linux006之帮助命令

linux帮助命令简介&#xff1a; linux的命令是非常多的&#xff0c;光靠人是记不住的&#xff0c;在工作中一般都会去网上查&#xff0c;这是有外网的情况下&#xff0c;如果项目中不允许访问外网&#xff0c;那么linux的帮助命令就可以派上用场了&#xff0c; linux帮助命令是…...

编程日记 2023/2/12 19:29:22

【C++初阶】十三、模板进阶（总）|非类型模板参数|模板的特化|模板分离编译|模板总结（优缺点）

目录 一、非类型模板参数 二、模板的特化 2.1 模板特化概念 2.2 函数模板特化 2.3 类模板特化 2.3.1 全特化 2.3.2 偏特化 三、模板分离编译 四、模板总结&#xff08;优缺点&#xff09; 前言&#xff1a;之前模板初阶并没有把 C模板讲完&#xff0c;因为当时没有接触…...

编程日记 2023/2/12 19:28:14

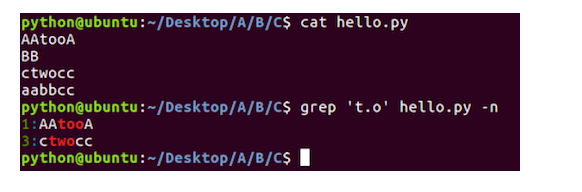
Linux之文本搜索命令

文本搜索命令学习目标能够知道文本搜索使用的命令1. grep命令的使用命令说明grep文本搜索grep命令效果图:2. grep命令选项的使用命令选项说明-i忽略大小写-n显示匹配行号-v显示不包含匹配文本的所有行-i命令选项效果图:-n命令选项效果图:-v命令选项效果图:3. grep命令结合正则表…...

编程日记 2023/2/12 19:27:05

微信小程序Springboot 校园拼车自助服务系统java

系统管理员&#xff1a; 管理员账户管理&#xff1a;在线对管理员的账户信息进行管理&#xff0c;包括对管理员信息的增加修改以及密码的修改等。 站内新闻管理&#xff1a;在后台对站内新闻信息进行发布&#xff0c;并能够对站内新闻信息进行删除修改等。 论坛版块管理&#x…...

编程日记 2023/2/12 19:25:50

【Unity3D 常用插件】Haste插件

一&#xff0c;Haste介绍 Haste插件是一款针对 Unity 3D 的 Everthing软件&#xff0c;可以实现基于名称快速定位对象的功能。Unity 3D 编辑器也自带了搜索功能&#xff0c;但是在 project视图 和 Hierarchy视图 中的对象需要分别查找&#xff0c;不支持模糊匹配。Haste插件就…...

编程日记 2023/2/12 19:24:42

【c++面试问答】全局变量和局部变量的区别

问题 C中的全局变量和局部变量有什么区别&#xff1f; 注&#xff1a;内容全部参考自文末的参考资料 全局变量和局部变量的区别 可以从以下4个角度来区分&#xff1a; 区别全局变量局部变量作用域全局作用域局部作用域内存分配全局变量在静态数据区静态局部变量在静态数据区…...

编程日记 2023/2/12 19:23:36

前端倒计时误差!

提示：记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来？二、五大解决方案1. 动态校准法（基础版）2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

编程新知 2025/9/8 23:14:43

【Linux】C语言执行shell指令

在C语言中执行Shell指令 在C语言中&#xff0c;有几种方法可以执行Shell指令&#xff1a; 1. 使用system()函数 这是最简单的方法&#xff0c;包含在stdlib.h头文件中&#xff1a; #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

编程新知 2025/11/20 18:42:48

Java - Mysql数据类型对应

Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

编程新知 2025/12/14 11:45:25

Springcloud：Eureka 高可用集群搭建实战（服务注册与发现的底层原理与避坑指南）

引言&#xff1a;为什么 Eureka 依然是存量系统的核心&#xff1f; 尽管 Nacos 等新注册中心崛起&#xff0c;但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制&#xff0c;是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

编程新知 2026/1/31 7:23:48

Axios请求超时重发机制

Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式&#xff1a; 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

编程新知 2025/10/13 2:26:14

什么是Ansible Jinja2

理解 Ansible Jinja2 模板 Ansible 是一款功能强大的开源自动化工具&#xff0c;可让您无缝地管理和配置系统。Ansible 的一大亮点是它使用 Jinja2 模板&#xff0c;允许您根据变量数据动态生成文件、配置设置和脚本。本文将向您介绍 Ansible 中的 Jinja2 模板&#xff0c;并通…...

编程新知 2026/2/6 1:00:25

AspectJ 在 Android 中的完整使用指南

一、环境配置&#xff08;Gradle 7.0 适配&#xff09; 1. 项目级 build.gradle // 注意&#xff1a;沪江插件已停更&#xff0c;推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

编程新知 2025/7/7 22:33:57

使用 SymPy 进行向量和矩阵的高级操作

在科学计算和工程领域&#xff0c;向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能&#xff0c;能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作&#xff0c;并通过具体…...

编程新知 2026/1/31 12:47:41

在Mathematica中实现Newton-Raphson迭代的收敛时间算法（一般三次多项式）

考察一般的三次多项式&#xff0c;以r为参数&#xff1a; p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]&#xff1b; 此多项式的根为&#xff1a; 尽管看起来这个多项式是特殊的&#xff0c;其实一般的三次多项式都是可以通过线性变换化为这个形式…...

编程新知 2026/1/30 3:24:00

Golang——7、包与接口详解

包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

编程新知 2026/2/2 16:55:46