树二叉树
树
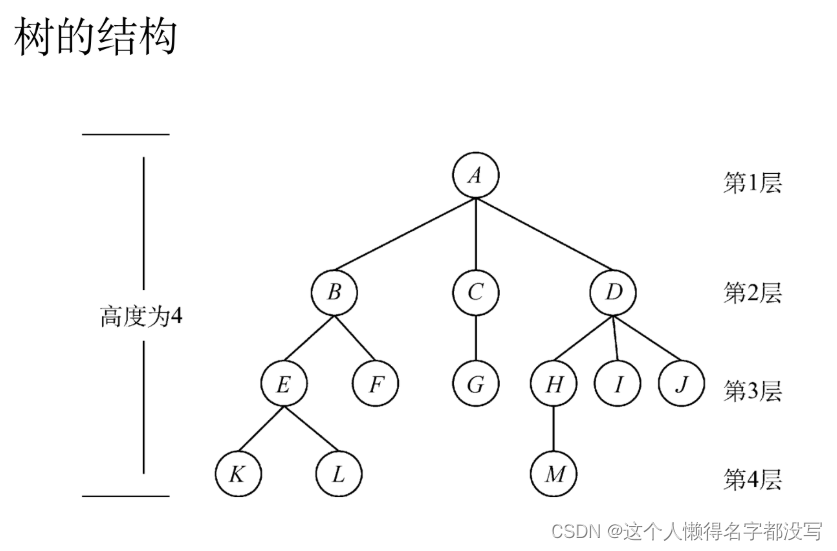
树是 n(n≥0)个结点的有限集。当 n = 0时,称为空树。在任意一颗非空树中应满足:
(1)有且仅有一个特定的称为根的结点。
(2)当 n > 1时,其余结点可分为 m(m > 0)个互不相交的有限集T1, T2, …, Tm,其中每个集合本身又是一棵树,并且称为根的子树。
树作为一种逻辑结构,同时也是一种分层结构,具有以下两个特点:
(1)树的根结点没有前驱,除根结点外的所有结点有且只有一个前驱。
(2)树中所有结点可以有零个或多个后继。
二叉树
二叉树是另一种树形结构,其特点是每个结点至多只有两颗字数(即二叉树中不存在度大于2的结点),并且二叉树的子树有左右之分,其次序不能任意颠倒。
与树相似,二叉树也以递归的形式定义,二叉树是 n(n ≥ 0)个结点的有限集合:
(1)或者为空二叉树,即 n = 0。
(2)或者由一个根结点和两个互不相交的被称为根的左子树和右子树组成。左子树和右子树分别是一颗二叉树。
满二叉树:
如果一棵二叉树只有度为0的节点和度为2的节点,并且度为0的节点在同一层上,则这棵二叉树为满二叉树 。
完全二叉树:
深度为k,有n个节点的二叉树当且仅当其每一个节点都与深度为k的满二叉树中编号从1到n的节点一一对应时,称为完全二叉树。
普通二叉树:
二叉查找树:
二叉查找树又称二叉排序树或者二叉搜索树。
特点:
- 每个节点上最多有两个子节点。
- 左子树上所有节点的值都小于根节点的值。
- 右子树上所有节点的值都大于根节点的值。
目的:
- 提高检索数据的性能。
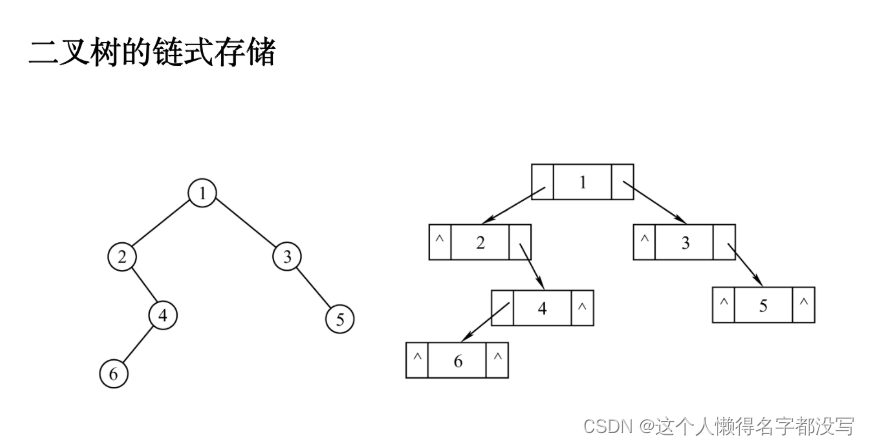
二茶树的链式存储
typedef char BiElemType;
typedef struct BiTNode {BiElemType data;struct BiTNode *lchild;struct BiTNode *rchild;
}
二叉树建树
#include <stdio.h>
#include <stdlib.h>typedef char BiElemType;
// 树结点
typedef struct BiTNode {// 数据BiElemType data;// 左子树struct BiTNode *lchild;// 右子树struct BiTNode *rchild;} BiTNode, *BiTree;// 用于构建辅助链队结点
typedef struct LinkNode {// 用于存储树的某一个结点的地址BiTree p_tree;struct LinkNode *next;
} LinkNode;int main() {// 创建树根BiTree Tree = NULL;// 用来指向新申请的树结点BiTree tree_new_node;// 队列头 队列尾 队列新结点 当前树的父结点(要插入结点的位置)LinkNode *q_head = NULL, *q_tail = NULL, *q_new_node = NULL, *q_cur = NULL;char c;while (scanf("%c", &c)) {if ('\n' == c) {break;}// 申请树结点// calloc 申请空间并对空间进行初始化为0tree_new_node = (BiTree) calloc(1, sizeof(BiTNode));tree_new_node->data = c;// 队列新结点q_new_node = (LinkNode *) calloc(1, sizeof(LinkNode));// 新结点p_tree存储新的树结点地址q_new_node->p_tree = tree_new_node;q_new_node->next = NULL;// 如果树为空if (NULL == Tree) {// 树根Tree = tree_new_node;// 队首q_head = q_new_node;// 队尾q_tail = q_new_node;// 当前树的父结点(要插入结点的位置)q_cur = q_new_node;// 结束本次循环continue;} else {// 新结点放入队列中q_tail->next = q_new_node;// 新结点成为新尾部q_tail = q_new_node;}// 当前父结点插入左子树if (NULL == q_cur->p_tree->lchild) {q_cur->p_tree->lchild = tree_new_node;} else if (NULL == q_cur->p_tree->rchild) {q_cur->p_tree->rchild = tree_new_node;//当前父结点左右子树都有了 队列下一个结点作为树的父结点q_cur = q_cur->next;}}return 0;
}
二叉树遍历
深度优先遍历
二叉树的深度优先遍历有三种方式,前序遍历、中序遍历、后序遍历。
- 前序遍历是先打印自身,再打印左子树,再打印右子树。
- 中序遍历是先打印左子树,再打印自身,再打印右子树,中序遍历相当于把树压扁。
- 后序遍历是先打印左子树,再打印右子树,最后打印当前结点。
#include <stdio.h>
#include <stdlib.h>typedef char BiElemType;
// 树结点
typedef struct BiTNode {// 数据BiElemType data;// 左子树struct BiTNode *lchild;// 右子树struct BiTNode *rchild;} BiTNode, *BiTree;// 用于构建辅助链队结点
typedef struct LinkNode {// 用于存储树的某一个结点的地址BiTree p_tree;struct LinkNode *next;
} LinkNode;/** 先序遍历* 用递归思想解决 把每个结点看作一棵树*/
void pre_order(BiTree p) {if (NULL != p) {// 本身printf("%c", p->data);// 左子树pre_order(p->lchild);// 右子树pre_order(p->rchild);}
}/** 中序遍历* 用递归思想解决 把每个结点看作一棵树*/
void in_order(BiTree p) {if (NULL != p) {// 左子树in_order(p->lchild);// 本身printf("%c", p->data);// 右子树in_order(p->rchild);}
}/** 后续遍历* 用递归思想解决 把每个结点看作一棵树*/
void post_order(BiTree p) {if (NULL != p) {// 左子树post_order(p->lchild);// 右子树post_order(p->rchild);// 本身printf("%c", p->data);}
}int main() {// 创建树根BiTree Tree = NULL;// 用来指向新申请的树结点BiTree tree_new_node;// 队列头 队列尾 队列新结点 当前树的父结点(要插入结点的位置)LinkNode *q_head = NULL, *q_tail = NULL, *q_new_node = NULL, *q_cur = NULL;char c;while (scanf("%c", &c)) {if ('\n' == c) {break;}// 申请树结点// calloc 申请空间并对空间进行初始化为0tree_new_node = (BiTree) calloc(1, sizeof(BiTNode));tree_new_node->data = c;// 队列新结点q_new_node = (LinkNode *) calloc(1, sizeof(LinkNode));// 新结点p_tree存储新的树结点地址q_new_node->p_tree = tree_new_node;q_new_node->next = NULL;// 如果树为空if (NULL == Tree) {// 树根Tree = tree_new_node;// 队首q_head = q_new_node;// 队尾q_tail = q_new_node;// 当前树的父结点(要插入结点的位置)q_cur = q_new_node;// 结束本次循环continue;} else {// 新结点放入队列中q_tail->next = q_new_node;// 新结点成为新尾部q_tail = q_new_node;}// 当前父结点插入左子树if (NULL == q_cur->p_tree->lchild) {q_cur->p_tree->lchild = tree_new_node;} else if (NULL == q_cur->p_tree->rchild) {q_cur->p_tree->rchild = tree_new_node;//当前父结点左右子树都有了 队列下一个结点作为树的父结点q_cur = q_cur->next;}}// 先序遍历printf("Pre Order: ");pre_order(Tree);printf("\n");// 中序遍历printf("In Order: ");in_order(Tree);printf("\n");// 后序遍历printf("Post Order: ");post_order(Tree);printf("\n");return 0;
}
输入结果:
abcdefghi
Pre Order: abdhiecfg
In Order: hdibeafcg
Post Order: hidebfgcaProcess finished with exit code 0
广度优先遍历
层次遍历是一种广度优先遍历,层次遍历与层次建树的原理非常相似。层次遍历必须试用辅助队列。
#include <stdio.h>
#include <stdlib.h>typedef char BiElemType;
// 树结点
typedef struct BiTNode {// 数据BiElemType data;// 左子树struct BiTNode *lchild;// 右子树struct BiTNode *rchild;} BiTNode, *BiTree;// 用于构建辅助链队结点
typedef BiTNode ElemType;
typedef struct LinkNode {ElemType *data;struct LinkNode *next;
} LinkNode;
typedef struct LinkQueue {LinkNode *front, *rear;
} LinkQueue;/** 队列初始化*/
void init_queue(LinkQueue &Q) {Q.front = Q.rear = (LinkNode *) malloc(sizeof(LinkNode));Q.front->next = NULL;
}/** 队列是否为空*/
bool queue_empty(LinkQueue Q) {return Q.front == Q.rear;
}/** 入队*/
void enqueue(LinkQueue &Q, BiTree T) {LinkNode *s = (LinkNode *) malloc(sizeof(LinkNode));s->data = T;s->next = NULL;Q.rear->next = s;Q.rear = s;
}/** 出队*/
bool dequeue(LinkQueue &Q, BiTree &T) {// 队列为空if (queue_empty(Q)) {return false;}LinkNode *p = Q.front->next;T = p->data;Q.front->next = p->next;if (Q.rear == p) {Q.rear = Q.front;}free(p);return true;
}/** 层序遍历** 跟层次建树几乎一样 用辅助队列实现*/
void level_order(BiTree T) {LinkQueue Q;init_queue(Q);// 树根入队enqueue(Q, T);// 从队列出队的树结点BiTree p;// 队列不为空while (!queue_empty(Q)) {// 出队dequeue(Q, p);putchar(p->data);// 判断当前结点是否有左孩子if (NULL != p->lchild) {// 左孩子入队enqueue(Q, p->lchild);}// 判断当前结点是否有右孩子if (NULL != p->rchild) {// 右孩子入队enqueue(Q, p->rchild);}}}int main() {// 创建树根BiTree Tree = NULL;// 用来指向新申请的树结点BiTree tree_new_node;// 队列头 队列尾 队列新结点 当前树的父结点(要插入结点的位置)LinkNode *q_head = NULL, *q_tail = NULL, *q_new_node = NULL, *q_cur = NULL;char c;while (scanf("%c", &c)) {if ('\n' == c) {break;}// 申请树结点// calloc 申请空间并对空间进行初始化为0tree_new_node = (BiTree) calloc(1, sizeof(BiTNode));tree_new_node->data = c;// 队列新结点q_new_node = (LinkNode *) calloc(1, sizeof(LinkNode));// 新结点p_tree存储新的树结点地址q_new_node->data = tree_new_node;q_new_node->next = NULL;// 如果树为空if (NULL == Tree) {// 树根Tree = tree_new_node;// 队首q_head = q_new_node;// 队尾q_tail = q_new_node;// 当前树的父结点(要插入结点的位置)q_cur = q_new_node;// 结束本次循环continue;} else {// 新结点放入队列中q_tail->next = q_new_node;// 新结点成为新尾部q_tail = q_new_node;}// 当前父结点插入左子树if (NULL == q_cur->data->lchild) {q_cur->data->lchild = tree_new_node;} else if (NULL == q_cur->data->rchild) {q_cur->data->rchild = tree_new_node;//当前父结点左右子树都有了 队列下一个结点作为树的父结点q_cur = q_cur->next;}}// 层次遍历printf("Level Order: ");level_order(Tree);return 0;
}
输出结果:
abcdefghi
Level Order: abcdefghiProcess finished with exit code 0
相关文章:

树二叉树
树 树是 n(n≥0)个结点的有限集。当 n 0时,称为空树。在任意一颗非空树中应满足: (1)有且仅有一个特定的称为根的结点。 (2)当 n > 1时,其余结点可分为 m&…...
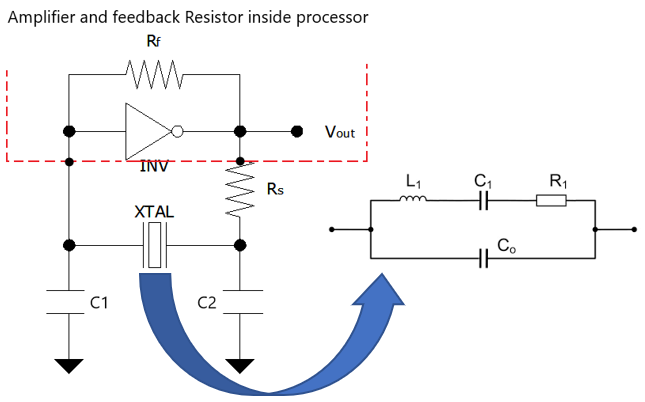
无源晶振振荡电路失效问题分析与解决策略
无源晶振(晶体谐振器)在电子设备中扮演着至关重要的角色,为数字电路提供稳定的时钟信号。然而,振荡电路一旦失效,可能会导致整个系统运行不正常。晶发电子将从三个主要方面分析无源晶振振荡电路失效的问题,…...

LIMS系统在汽车第三方检测实验室的应用
随着汽车行业的快速发展,汽车第三方检测实验室的工作量不断增加,对实验室的管理效率和数据准确性提出了更高的要求。LIMS系统的引入可以实现实验室的全面数字化管理,提高工作效率,降低运营成本,并提升数据质量与决策支…...

positivessl泛域名https证书
PositiveSSL,作为Sectigo旗下的子品牌,一直以来颁发的https数字证书产品性价比较高,适合大多数个人网站和中小型企业。其中,DV基础型的泛域名https证书以申请简单、颁发速度快、价格低受到众多用户的欢迎。今天就随SSl盾小编了解P…...

MySQL bin-log日志恢复数据
目录 一、开启二进制日志 二、检查二进制日志是否开启 三、使用二进制日志备份和恢复 使用二进制日志备份恢复前先创建备份: 应用二进制日志: 扩展用法: 四、常见命令和操作 五. 使用 mysqlbinlog 工具查看二进制日志 1. 查看二进制…...

Linux网络命令——netstat
netstat是Linux系统中非常有用的网络工具,被称为是网络监控中的军工刀,足见其地位。 传统上,它用于问题确定而不是性能测量,但是也可用于查看网络上的流量,以确定性能问题是否由于网络阻塞引起。 netstat用于显示与I…...

手机怎么压缩图片?通过三种压缩操作
手机怎么压缩图片?在智能手机日益普及的今天,拍照分享已成为日常生活的一部分。然而,高质量的照片往往占用较大的存储空间,且在网络上传输时速度较慢。那么,如何在手机上压缩图片呢?本文将介绍三种实用的手…...

分布式CAP、BASE理论务必了解一下
分布式系统理论是计算机科学中的一个重要分支,它关注如何设计和实现能够跨多个物理或逻辑位置运行的系统。在分布式系统中,CAP定理和BASE理论是两个非常著名的理论,它们分别描述了分布式系统设计中的一些基本约束和原则。 CAP定理 CAP定理&…...

spring最常用的注解
核心注解 Component 描述:将类标记为 Spring 组件,以便自动检测。用途:通常用于标注服务类或其他支持类。 Controller 描述:将类标记为 Spring MVC 控制器。用途:用于处理 Web 请求。 Service 描述:将类标记…...
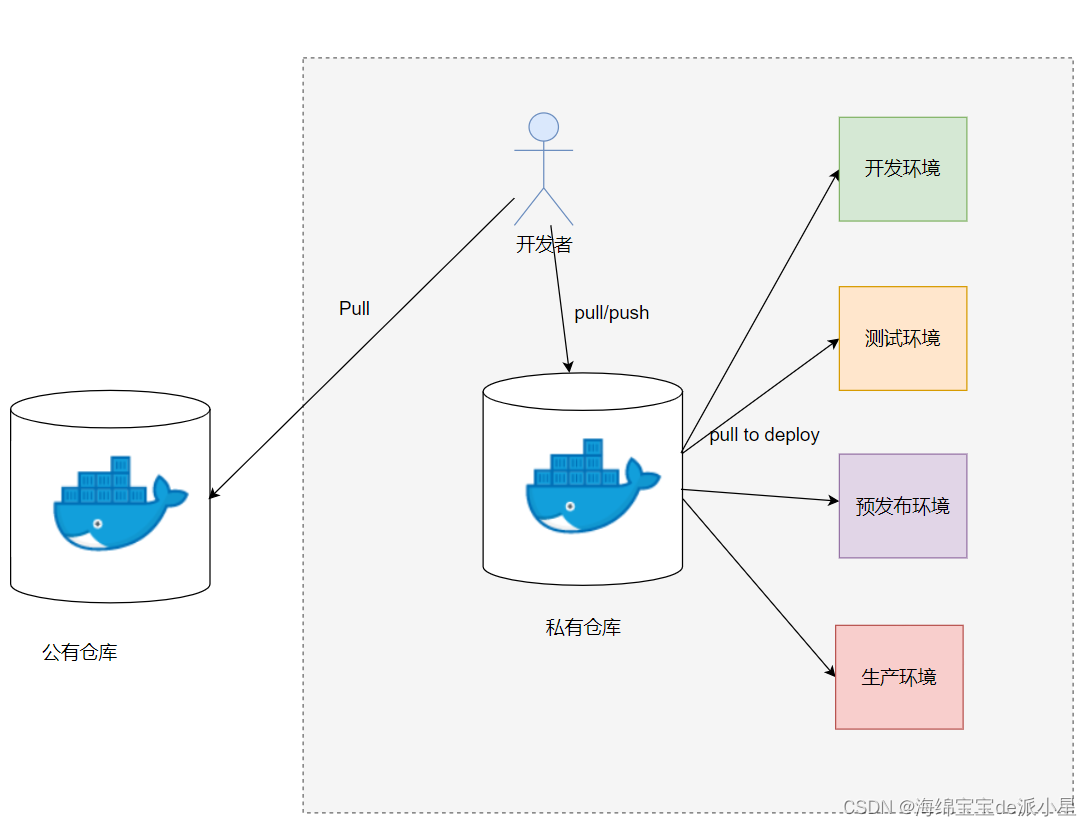
Docker:认识镜像仓库及其命令
文章目录 Docker Registry什么是Docker Registry 镜像仓库工作机制使用流程实际使用方法仓库的拉取机制 常用的镜像仓库---DockerHub什么是DockerHub私有仓库 镜像仓库命令docker logindocker pulldocker pushdocker searchdocker logout Docker Registry 什么是Docker Regist…...

使用 Django 创建 App
文章目录 步骤 1:创建 Django 项目步骤 2:创建 App步骤 3:配置 App步骤 4:编写代码步骤 5:运行服务器 在 Django 中,App 是组织代码的基本单元,它可以包含模型、视图、模板等组件,帮…...

java定时任务 设置开始时间、结束时间;每周一、四、六执行;并且隔n周执行。最后计算所有执行时间
java定时任务 设置开始时间、结束时间;每周一、四、六执行;并且隔n周执行。最后计算所有执行时间) 定时任务需求程序设计依赖引入程序一、计算开始时间那周的周一时间二、根据executeTime和weekList.get(n),计算每个cron表达式。三、根据一和…...

linux的持续性学习
安装php 第一步:配置yum源 第二步:下载php。 yum install php php-gd php-fpm php-mysql -y 第三步:启动php。 systemctl start php-fpm 第四步:检查php是否启动 lsof -i :9000 计划任务 作用&am…...

MyBatis:概念简章
1. hello world 配置文件:mybatis-config.xml(核心配置文件,用于配置连接的数据库信息)(一般一个)XxxMapper.xml 该文件用于操作表(执行sql语句)(一张表一个)…...

有什么接码平台比较好用的
接码平台,也被称作短信接收平台或虚拟号码服务,主要是提供可以接收短信验证码的虚拟手机号码服务。这种服务通常被用于需要在网络平台上注册大量账号的情况,如营销推广、应用测试或是海淘购物时所需的手机号验证。下面将推荐几个较为好用的接…...
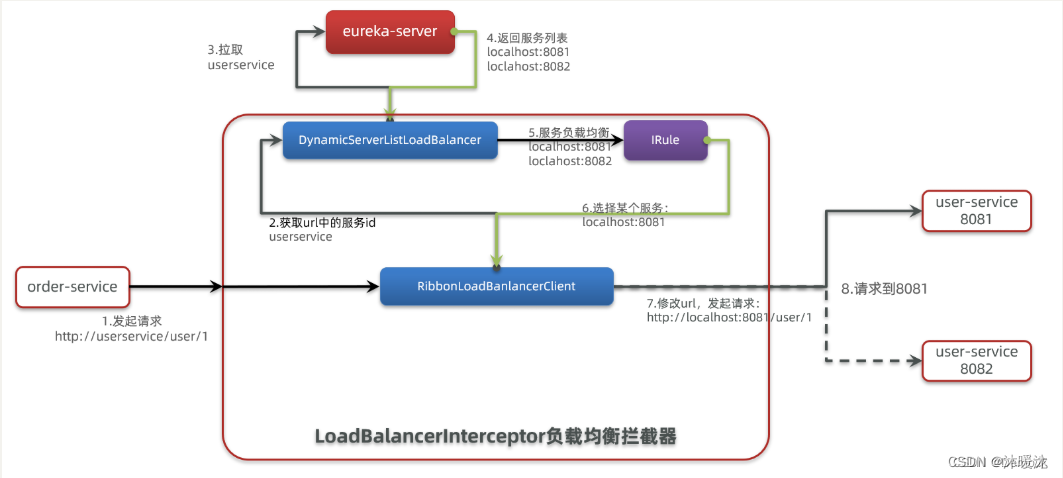
微服务之负载均衡器
1、负载均衡介绍 负载均衡就是将负载(工作任务,访问请求)进行分摊到多个操作单元(服务器,组件)上 进行执行。 根据负载均衡发生位置的不同, 一般分为服务端负载均衡和客户端负载均衡。 服务端负载均衡指的是发生在服务提供者一方ÿ…...

《时间管理九段》前四阶段学习笔记
文章目录 0.何谓时间管理九段0.1 第一段--把一件事做好0.2 第二段--把一天过好0.3 第三段--掌控两周内的固定日程0.4 第四段--掌控两周内的弹性时间0.5 第五段--科学管理3个月的项目事件0.6 第六段--实现一年的梦想0.7 第七段--明确一生的愿景0.8 第八段--正确补充和释放自身能…...
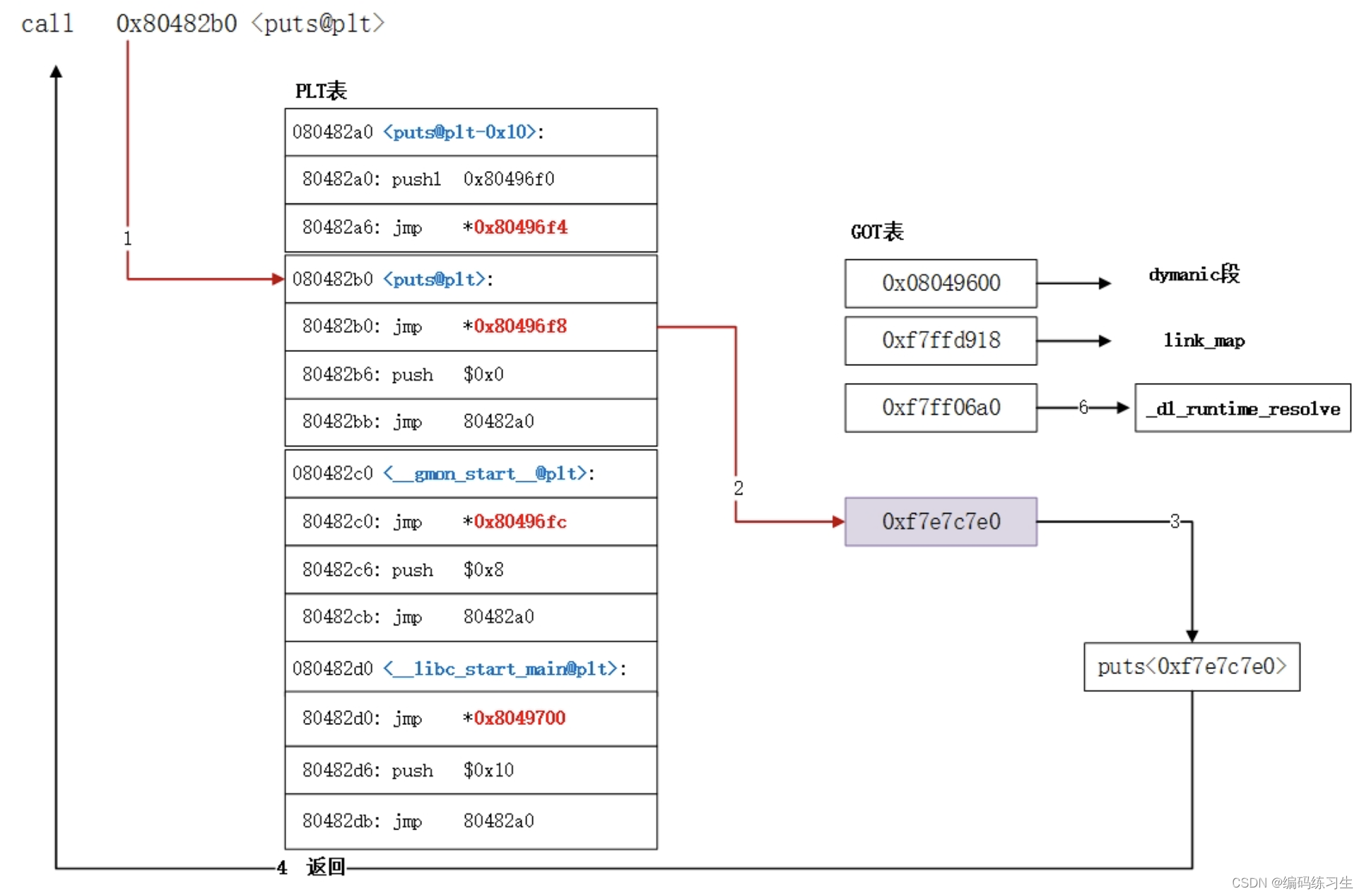
LLVM Cpu0 新后端5 静态重定位 动态重定位
想好好熟悉一下llvm开发一个新后端都要干什么,于是参考了老师的系列文章: LLVM 后端实践笔记 代码在这里(还没来得及准备,先用网盘暂存一下): 链接: https://pan.baidu.com/s/1yLAtXs9XwtyEzYSlDCSlqw?…...

旅游卡是项目还是骗局?还是实实在在的旅游项目?
旅游卡是一个实实在在的旅游项目,而非骗局。以下是我对旅游卡项目的几点分析: 项目实质: 旅游卡项目是由国内外多条旅游线路整合而成的卡片,为旅游者提供方便、实惠的旅游方式。持有旅游卡,可以完全抵销跟团游线路中的…...

大模型+RAG,全面介绍!
1 、介绍 大型语言模型(LLMs)在处理特定领域或高度专业化的查询时存在局限性,如生成不正确信息或“幻觉”。缓解这些限制的一种有前途的方法是检索增强生成(RAG),RAG就像是一个外挂,将外部数据…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

基于Uniapp开发HarmonyOS 5.0旅游应用技术实践
一、技术选型背景 1.跨平台优势 Uniapp采用Vue.js框架,支持"一次开发,多端部署",可同步生成HarmonyOS、iOS、Android等多平台应用。 2.鸿蒙特性融合 HarmonyOS 5.0的分布式能力与原子化服务,为旅游应用带来…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

深度学习习题2
1.如果增加神经网络的宽度,精确度会增加到一个特定阈值后,便开始降低。造成这一现象的可能原因是什么? A、即使增加卷积核的数量,只有少部分的核会被用作预测 B、当卷积核数量增加时,神经网络的预测能力会降低 C、当卷…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...
