一些简单却精妙的算法
文章目录
- 1.树状数组
- 2.红黑树
- 3.星星打分
- 4.欧几里得算法
- 5.快速幂
- 6.并查集
在编程的世界里,简洁的代码往往隐藏着深邃的智慧。一起来看看那些看似简单,实则精妙绝伦的代码片段,体会编程语言的优雅与力量。
1.树状数组
int lowbit(int x)
{ return x&-x;
}
树状数组里的这个,太精妙了,树状数组使区间求和复杂度降低到了log(n),发明这段代码的人一定是个天才,而这个lowbit恰恰是最精妙的一部分,可以准确的找到我们需要加的部分,巧妙的利用了计算机的位运算。
2.红黑树
defun rbt-balance (tree) "Balance the rbtree list TREE." (pcase tree (`(B (R (R ,a ,x ,b) ,y ,c) ,z ,d) `(R (B ,a ,x ,b) ,y (B ,c ,z ,d))) (`(B (R ,a ,x (R ,b ,y ,c)) ,z ,d) `(R (B ,a ,x ,b) ,y (B ,c ,z ,d))) (`(B ,a ,x (R (R ,b ,y ,c) ,z ,d)) `(R (B ,a ,x ,b) ,y (B ,c ,z ,d))) (`(B ,a ,x (R ,b ,y (R ,c ,z ,d))) `(R (B ,a ,x ,b) ,y (B ,c ,z ,d))) (_ tree))) (defun rbt-insert- (x s) "Auxilary function of rbt-insert." (pcase s (`nil `(R nil ,x nil)) (`(,color ,a ,y ,b) (cond ((< x y) (rbt-balance `(,color ,(rbt-insert- x a) ,y ,b))) ((> x y) (rbt-balance `(,color ,a ,y ,(rbt-insert- x b)))) (t s))) (_ (error "Expected tree: %S" s)))) (defun rbt-insert (x s) "Insert S to rbtree X." (pcase (rbt-insert- x s) (`(,_ ,a ,y ,b) `(B ,a ,y ,b)) (_ (error "Internal error: %S" s))))
3.星星打分
function getRating(rating) { if(rating > 5 || rating < 0) throw new Error('数字不在范围内'); return '★★★★★☆☆☆☆☆'.substring(5 - rating, 10 - rating );
}
这种实现方式之所以精妙,是因为它利用了字符串的固定模式和 substring 方法的灵活性来生成不同数量的星星,而不需要使用循环或额外的逻辑来逐个添加或删除星星。这种方法简洁且高效,特别是在需要频繁生成星级评分表示时。
然而,这段代码也有局限性,它假设评分总是整数,并且只支持0到5的评分范围。如果需要支持小数评分或更广泛的评分范围,这段代码将需要相应的调整。
4.欧几里得算法
function gcd(a, b) { return b ? gcd(b, a % b) : a;
}
这种递归实现的欧几里得算法非常简洁且高效。它利用了数学上的一个性质:两个整数的最大公约数与它们的余数和较小数的最大公约数相同。即 gcd(a, b) = gcd(b, a % b)。
5.快速幂
function fastPower(b, n) { if (n === 0) return 1; const result = fastPower(b, Math.floor(n / 2)); return n % 2 === 0 ? result * result : b * result * result;
用于高效地计算 b 的 n 次方。快速幂算法特别适用于计算大幂次的情况,因为它将幂次的计算复杂度从 O(n) 降低到 O(log n)。
6.并查集
int find(int x){ x==parent[x]?:find(parent[x]);
}
并查集(Union-Find)数据结构中的 find 函数的简洁实现。
递归查找:find 函数通过递归的方式查找元素 x 的根节点。递归会在元素与其父节点不同时,继续查找父节点的父节点,直到找到一个元素其父节点是它自己的元素,即根节点。
路径压缩:代码中的三元运算符 ?: 实现了路径压缩技术。当 x 不是其根节点时(即 x != parent[x]),find 函数会调用自身并传入 parent[x] 作为参数。在递归返回的过程中,每个节点的父节点指针都被更新为最终的根节点,这样可以减少后续查找操作的深度。
相关文章:

一些简单却精妙的算法
文章目录 1.树状数组2.红黑树3.星星打分4.欧几里得算法5.快速幂6.并查集 在编程的世界里,简洁的代码往往隐藏着深邃的智慧。一起来看看那些看似简单,实则精妙绝伦的代码片段,体会编程语言的优雅与力量。 1.树状数组 int lowbit(int x) { …...

git多账号使用报错:You don‘t have permissions to push to “xxx/xxxx“ onGitHub. Would
git多账号使用报错:You don’t have permissions to push to “xxx/xxxx” onGitHub. Would 有的时候我们有两个甚至多个git账号(公司的git账号和自己的github),为了不混淆提交,我们需要在提交之前查看自己的git账号必…...
2023年12月真题C语言软件编程等级考试三级(含详细解析答案))
中国电子学会(CEIT)2023年12月真题C语言软件编程等级考试三级(含详细解析答案)
中国电子学会(CEIT)考评中心历届真题(含解析答案) C语言软件编程等级考试三级 2023年12月 编程题五道 总分:100分一、因子问题(20分) 任给两个正整数N、M,求一个最小的正整数a,使得a和(M-a)都是N的因子。 时间限制: 10000ms 内存限制: 65536kb 输入 包括两个整…...

多线程爬取百度图片
爬取网页图片 import urllib.parse import requests import os import time from concurrent.futures import ThreadPoolExecutorheaders {"User-Agent":"Mozilla/5.0 (Windows NT 10.0; Win64; x64) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/125.0.0.0…...

RK3568-修改fiq-debugger调试串口
瑞芯微SDK默认将uart2_m0作为调试串口,以下方法将调试串口修改为uart5_m1。修改bootloader 修改/OK3568-linux-source/rkbin/tools/ddrbin_param.txt文件,5表示串口5。1表示复用m1。执行./ddrbin_tool ddrbin_param.txt ../bin/rk35/rk3568_ddr_1560MHz_v1.11.bin命令修改ub…...

我们离成功有多远呢?只要能完成自己阶段性的目标就算是一次成功
做起一个账号,带好一个团队,经营好一家公司,似乎这些都能叫成功,成功的定义可大可小,而我认为只要能完成自己阶段性的目标就算是一次成功,毕竟每个人学历、背景、阅历、资源、认知都不同,很难同…...

Golang 避坑指南
文章目录 1. Channel 与 Goroutine 泄露1.1 发送不接收1.2 接收不发送1.3 nil channel2. 跳出 for-switch 或 for-select 3.for 迭代变量3.1 闭包中的for迭代变量3.2 for range 迭代变量 4. 循环内的 defer5.defer 函数的参数值6.nil interface 和 nil interface 值7.结构体指针…...
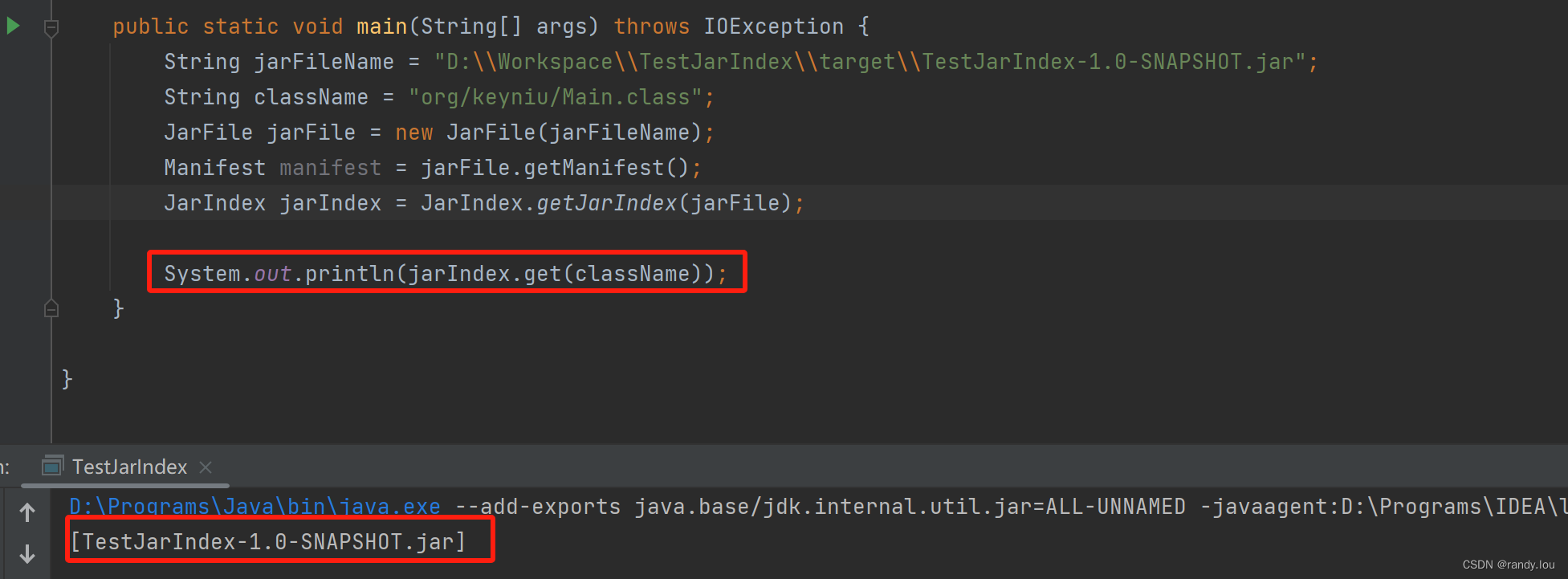
Java核心: JarIndex的使用
在讲解Java类加载器的时候,我们发现URLClassLoader加载类或资源时通过访问ClassPath下的每一个路径,来确定类是否存在的,假设我们执行的命令是这样的 java -classpath D:\DiveInSpring\target\classes;C:\lib\spring-expression.jar;C:\lib\…...

1052 卖个萌(测试点1,2)
solution 想要输出\需要用\\才能输出,即 cout << "Are you kidding me? \\/" << endl;测试点1,2:输入序号小于1的非法情况 #include<iostream> #include<string> #include<map> using namespace…...

Vue 3与ESLint、Prettier:构建规范化的前端开发环境
title: Vue 3与ESLint、Prettier:构建规范化的前端开发环境 date: 2024/6/11 updated: 2024/6/11 publisher: cmdragon excerpt: 这篇文章介绍了如何在Vue 3项目中配置ESLint和Prettier以统一代码风格,实现代码规范性与可读性的提升。通过设置规则、解…...

npm安装依赖过慢
今天在使用npm安装taro框架的依赖时,速度慢到吐血,使用了淘宝镜像源依然很慢,安装一个多小时没反应,最后清理了缓存再次安装速度就快很多了,因此解决方法大致有两种: 使用淘宝镜像源 原域名: ht…...

计算机毕业设计 | SpringBoot+vue的教务管理系统
1,绪论 1.1 项目背景 在这个资讯高度发展的时代,资讯管理变革已经是一个更为宽泛、更为全面的潮流。为了保证中国的可持续发展,随着信息化技术的不断进步,教务管理体系也在不断完善。与此同时,伴随着信息化的飞速发展…...

深入探索深度学习的验证集:必要还是可选?
深入探索深度学习的验证集:必要还是可选? 在深度学习项目的设计和实施过程中,数据通常被划分为训练集、测试集,以及有时的验证集。尽管在一些研究中,我们可能看到只有训练集和测试集被使用,验证集的作用及…...

初识C++ · 反向迭代器简介
目录 前言 反向迭代器的实现 前言 继模拟实现了list和vector之后,我们对迭代器的印象也是加深了许多,但是我们实现的都是正向迭代器,还没有实现反向迭代器,那么为什么迟迟不实现呢?因为难吗?实际上还好。…...

fastapi学习前置知识点
前置知识点 FastApi:一个用于构建API的现代、快速(高性能)的web框架。 FastApi是建立在Pydantic和Starlette基础上,Pydantic是一个基于Python类型提示来定义数据验证、序列化和文档的库。Starlette是一种轻量级的ASGI框架/工具包…...

机器学习常见知识点 1:Baggin集成学习技术和随机森林
文章目录 1、集成学习a.BaggingBagging的工作原理1. 自助采样(Bootstrap Sampling)2. 训练多个基学习器3. 聚合预测 Bagging的优点Bagging的缺点应用场景 b.Boosting 2、决策树3、随机森林随机森林的核心概念1. 集成学习2. 决策树 构建随机森林的步骤1. …...

容器(Docker)安装
centos安装Docker sudo yum remove docker* sudo yum install -y yum-utils#配置docker的yum地址 sudo yum-config-manager \ --add-repo \ http://mirrors.aliyun.com/docker-ce/linux/centos/docker-ce.repo#安装指定版本 - 可以根据实际安装版本 sudo yum install -y docke…...

前端JS必用工具【js-tool-big-box】学习,获取当前浏览器向上滚动还是向下滚动,获取当前距离顶部和底部的距离
这一小节,我们说一下 js-tool-big-box 添加的最新工具方法,在日常前端开发工作中,如果网页很长,我们就需要获取当前浏览器是在向上滚动,还是向下滚动。如果向上滚动,滚动到0的时候呢,需要做一些…...

【python】flask 框架
python flask 框架 flask是一个轻量级的python后端框架 (Django, tornado, flask) 官网:欢迎来到 Flask 的世界 — Flask中文文档(3.0.x) 安装:pip install Flask -i https://pypi.douban.com 常识: http,默认端口号为80; https,默认端口号…...

Word中插入Mathtype右编号,调整公式与编号的位置
当你已经将mathtype内置于word后,可以使用右编号快速插入公式 但是往往会出现公式和编号出现的位置或之间的距离不合适 比如我在双栏下插入公式,会发现插入的公式与编号是适用于单栏的 解决办法: 开始->样式->MTDisplayLquation -&g…...

国防科技大学计算机基础课程笔记02信息编码
1.机内码和国标码 国标码就是我们非常熟悉的这个GB2312,但是因为都是16进制,因此这个了16进制的数据既可以翻译成为这个机器码,也可以翻译成为这个国标码,所以这个时候很容易会出现这个歧义的情况; 因此,我们的这个国…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

Vue3 + Element Plus + TypeScript中el-transfer穿梭框组件使用详解及示例
使用详解 Element Plus 的 el-transfer 组件是一个强大的穿梭框组件,常用于在两个集合之间进行数据转移,如权限分配、数据选择等场景。下面我将详细介绍其用法并提供一个完整示例。 核心特性与用法 基本属性 v-model:绑定右侧列表的值&…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

屋顶变身“发电站” ,中天合创屋面分布式光伏发电项目顺利并网!
5月28日,中天合创屋面分布式光伏发电项目顺利并网发电,该项目位于内蒙古自治区鄂尔多斯市乌审旗,项目利用中天合创聚乙烯、聚丙烯仓库屋面作为场地建设光伏电站,总装机容量为9.96MWp。 项目投运后,每年可节约标煤3670…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

论文笔记——相干体技术在裂缝预测中的应用研究
目录 相关地震知识补充地震数据的认识地震几何属性 相干体算法定义基本原理第一代相干体技术:基于互相关的相干体技术(Correlation)第二代相干体技术:基于相似的相干体技术(Semblance)基于多道相似的相干体…...

深入浅出深度学习基础:从感知机到全连接神经网络的核心原理与应用
文章目录 前言一、感知机 (Perceptron)1.1 基础介绍1.1.1 感知机是什么?1.1.2 感知机的工作原理 1.2 感知机的简单应用:基本逻辑门1.2.1 逻辑与 (Logic AND)1.2.2 逻辑或 (Logic OR)1.2.3 逻辑与非 (Logic NAND) 1.3 感知机的实现1.3.1 简单实现 (基于阈…...
