Amortized bootstrapping via Automorphisms
参考文献:
- [MS18] Micciancio D, Sorrell J. Ring packing and amortized FHEW bootstrapping. ICALP 2018: 100:1-100:14.
- [GPV23] Guimarães A, Pereira H V L, Van Leeuwen B. Amortized bootstrapping revisited: Simpler, asymptotically-faster, implemented. ASIACRYPT 2023 (6): 3-35.
- [DKM+24] De Micheli G, Kim D, Micciancio D, et al. Faster amortized FHEW bootstrapping using ring automorphisms. Public Key Cryptography 2024 (4): 322-353.
- Amortized FHEW bootstrapping:Nussbaumer Transform & Ring Packing
文章目录
- RNS-GSW
- Shrinking
- Amortized Bootstrapping
- RLWE‘ to RGSW
- Prime Cyclotomic Rings
- Decryption
- INTT
- msbExtract
- Counting
[GPV23] 和 [DKM+24] 都遵照 [MS18] 的思路:
- packing:将 n n n 个 LWE 密文打包成单个 RLWE 密文,系数编码,形如 ( b , a ) ∈ R q , n 2 (b,a) \in R_{q,n}^2 (b,a)∈Rq,n2,私钥 s ∈ R n s \in R_{n} s∈Rn
- decryption:把 s i s_i si 加密在 RGSW 密文中作为自举密钥,将多项式 a , b a,b a,b 的 DFT-form 加密在 RGSW 密文的指数上( q q q 阶乘法循环群),利用 RGSW 同态乘法(指数上的加法)计算常数 N T T ( a ) NTT(a) NTT(a) 和密文 N T T ( s ) NTT(s) NTT(s) 的 Hadamard-product,然后做同态 IDFT 获得 a ⋅ s + b a \cdot s+b a⋅s+b 各个系数的 RGSW 密文。
- msbExtract:最后把各个系数的 MSB 从 RGSW 密文中提出成为 LWE 密文。
[MS18] 使用二的幂次分圆环对应的 RGSW 密文(模数 q = 2 N q = 2N q=2N),将它搭建成支持模 q q q 加法的寄存器。使用数字分解和枚举技术,使得这个寄存器也支持模 q q q 数乘。为了快速计算 IDFT,[MS18] 使用 Nussbaumer Transform R q , n ≅ R q , n / m [ X ] / ( X m − Y ) → R q , n / m [ X ] / ( X k m − 1 ) R_{q,n} \cong R_{q,n/m}[X]/(X^m-Y) \to R_{q,n/m}[X]/(X^{km}-1) Rq,n≅Rq,n/m[X]/(Xm−Y)→Rq,n/m[X]/(Xkm−1),其中 n ≥ k m 2 n \ge km^2 n≥km2 并且 n , m , k n,m,k n,m,k 都是同一个素数的幂次,这就构造出了合适的 k m km km 次本原单位根 Y = X m ∈ R q , n / m Y=X^m \in R_{q,n/m} Y=Xm∈Rq,n/m,并且和 Y Y Y 的数乘就只是在 R q , n / m R_{q,n/m} Rq,n/m 环元素的系数旋转(重排 RGSW 寄存器)。
[MS18] 的均摊开销是 O ~ ( n ϵ ) \tilde O(n^\epsilon) O~(nϵ),然而隐藏常数 O ( 2 1 / ϵ ) O(2^{1/\epsilon}) O(21/ϵ) 过大,导致并不实用。[GPV23] 和 [DKM+24] 都使用 Galois 自同构来实现数乘,并且直接用 Incomplete NTT 而非 Nussbaumer Transform。区别在于:[GPV23] 使用了素数次卷积环的 RGSW 寄存器,[DKM+24] 使用了素数次分圆环的 RLWE 寄存器,后者的计算效率会高一些。
RNS-GSW
由于均摊 FHEW/TFHE 自举的噪声比盲旋转大得多,这导致寄存器的密文模数可能会超过机器字。[GPV23] 提出了 GSW 的 Double-CRT 变体,以提高计算效率。
[GPV23] 使用卷积环 R ~ : = Z [ X ] / ( X p − 1 ) \tilde R := \mathbb Z[X]/(X^p-1) R~:=Z[X]/(Xp−1),其中 p p p 是素数,称为 CLWE 问题。有文章指出它和素数次分圆环的 RLWE 一样难。对于 R : = Z [ X ] / ( Φ p ( X ) ) R := \mathbb Z[X]/(\Phi_p(X)) R:=Z[X]/(Φp(X)),其中 Φ p ( X ) = 1 + X + X 2 + ⋯ + X p − 1 \Phi_p(X) = 1+X+X^2+\cdots+X^{p-1} Φp(X)=1+X+X2+⋯+Xp−1,定义投影函数 L : R → R ~ L: R \to \tilde R L:R→R~(疑问:系数 a p − 1 a_{p-1} ap−1 不该存在吧):
L Q : ∑ i = 0 p − 1 a i X i → ∑ i = 0 p − 1 a i X i − ( [ p − 1 ] Q ⋅ ∑ i = 0 p − 1 a i ) ⋅ ∑ i = 0 p − 1 X i ( m o d Q ) L_Q: \sum_{i=0}^{p-1} a_i X^i \to \sum_{i=0}^{p-1} a_i X^i - \left([p^{-1}]_Q \cdot \sum_{i=0}^{p-1} a_i\right) \cdot \sum_{i=0}^{p-1} X^i \pmod{Q} LQ:i=0∑p−1aiXi→i=0∑p−1aiXi−([p−1]Q⋅i=0∑p−1ai)⋅i=0∑p−1Xi(modQ)
给定 RLWE 样本 ( a ′ , b ′ ) ∈ R Q 2 (a',b') \in R_Q^2 (a′,b′)∈RQ2,将它转换为 CLWE 样本 ( a : = L Q ( a ′ ) , b : = L Q ( ( 1 − X ) ⋅ b ′ ) ) ∈ R ~ Q 2 (a:=L_Q(a'), b:=L_Q((1-X)\cdot b')) \in \tilde R_Q^2 (a:=LQ(a′),b:=LQ((1−X)⋅b′))∈R~Q2
素数次卷积环的 RNS-GSW 如下,

在 RLWE 假设下,对于形如 X k X^k Xk 的消息是 CPA-IND 安全的。
Shrinking
对于 Digit 分解,Approximate Gadget Decomposition 可以减少分解数量,并且基本不增加噪声。但是对于 RNS 分解,由于不存在确切的 LSD,因此并不兼容。[GPV23] 提出了 Shrinking 技术,用于 RNS 的近似分解。
模数 Q = ∏ i = 1 l q i Q = \prod_{i=1}^l q_i Q=∏i=1lqi,令 d ∣ l d \mid l d∣l 是整数,定义 CRT Digit 为 D i = ∏ j = ( i − 1 ) k + 1 i k q j , 1 ≤ i ≤ d D_i = \prod_{j=(i-1)k + 1}^{ik}q_j, 1 \le i \le d Di=∏j=(i−1)k+1ikqj,1≤i≤d(就是分区 d d d 块),令 D = max { D i } D = \max\{D_i\} D=max{Di} 是上界。定义 Q i = Q / D i Q_i = Q/D_i Qi=Q/Di 和 Q ^ i = [ Q i − 1 ] D i \hat Q_i = [Q_i^{-1}]_{D_i} Q^i=[Qi−1]Di,那么令 g = ( Q 1 Q ^ 1 , ⋯ , Q d Q ^ d ) ∈ Z d g = (Q_1\hat Q_1, \cdots, Q_d\hat Q_d) \in \mathbb Z^d g=(Q1Q^1,⋯,QdQ^d)∈Zd 是 gadget vector,对应的分解 g − 1 ( a ) g^{-1}(a) g−1(a) 就是 { [ a ] D i } 1 ≤ i ≤ d \{[a]_{D_i}\}_{1\le i \le d} {[a]Di}1≤i≤d,满足 ⟨ g − 1 ( a ) , g ⟩ = a \langle g^{-1}(a), g\rangle = a ⟨g−1(a),g⟩=a
给定缩放因子 α ∈ Z Q \alpha \in \mathbb Z_Q α∈ZQ,对应的 RNS 表示是 α i = [ α ] D i \alpha_i = [\alpha]_{D_i} αi=[α]Di,然后定义 g α = ( Q 1 Q ^ 1 α 1 , ⋯ , Q d Q ^ d α d ) g_\alpha = (Q_1\hat Q_1\alpha_1, \cdots, Q_d\hat Q_d\alpha_d) gα=(Q1Q^1α1,⋯,QdQ^dαd),将它称为 scaled gadget vector。对于任意的 a ∈ R Q a \in R_Q a∈RQ,容易证明它满足 ⟨ g − 1 ( α − 1 a ) , g α ⟩ = a \langle g^{-1}(\alpha^{-1}a), g_\alpha\rangle = a ⟨g−1(α−1a),gα⟩=a
Shrinking 就是删除一部分 CRT Digit,做模切换,并相应的调整缩放因子
- 给定 scaled gadget 分解 a i = [ a ] D i , 1 ≤ i ≤ d a_i=[a]_{D_i}, 1 \le i \le d ai=[a]Di,1≤i≤d,它的缩放因子是 α \alpha α
- 给定 1 ≤ k < d 1 \le k < d 1≤k<d,定义 D ( k ) = ∏ i = 1 k D i D^{(k)} = \prod_{i=1}^k D_i D(k)=∏i=1kDi 和 Q ′ = Q / D ( k ) Q' = Q/D^{(k)} Q′=Q/D(k)
- 对于 k + 1 ≤ i ≤ d k+1 \le i \le d k+1≤i≤d,计算 a i − k ′ = a i ⋅ [ D ( k ) ] D i a_{i-k}' = a_i \cdot [D^{(k)}]_{D_i} ai−k′=ai⋅[D(k)]Di
- 输出 a j ′ , 1 ≤ j ≤ d − k a_j', 1\le j\le d-k aj′,1≤j≤d−k,它的缩放因子是 α ′ = α ⋅ [ ( D ( k ) ) − 1 ] Q ′ \alpha' = \alpha \cdot [(D^{(k)})^{-1}]_{Q'} α′=α⋅[(D(k))−1]Q′
如果 RNS-GSW 密文加密了 α ⋅ m \alpha \cdot m α⋅m,噪声 E E E,私钥分布是 S S S 亚高斯。那么执行 Shrinking 之后,加密 α ′ ⋅ m \alpha' \cdot m α′⋅m,噪声 O ( E / D ( k ) + p ⋅ S ) O(E/D^{(k)}+\sqrt p \cdot S) O(E/D(k)+p⋅S),其中 p p p 是 CLWE 中的素数次。
Amortized Bootstrapping
由于 [GPV23] 和 [DKM+24] 的整体思路是相同的,仅仅是使用的寄存器不同。现在只看看 [DKM+24] 是怎么工作的。
RLWE‘ to RGSW
[DKM+24] 使用 RLWE’ 寄存器,但是在计算同态乘法时需要 RGSW 密文。因此,需要把 RLWE’ 提升到 RGSW
使用 R L W E s k ′ ( s k 2 ) RLWE'_{sk}(sk^2) RLWEsk′(sk2) 作为提示(称为 evaluation key),那么给定 ( b , a ) = R L W E s k ( v i m ) (b,a) = RLWE_{sk}(v_i m) (b,a)=RLWEsk(vim),可以计算
( 0 , b ) + a ⊙ R L W E s k ′ ( s k 2 ) = R L W E s k ( v i m ⋅ s k + e ⋅ s k ) (0,b) + a \odot RLWE_{sk}'(sk^2) = RLWE_{sk}(v_i m \cdot sk + e \cdot sk) (0,b)+a⊙RLWEsk′(sk2)=RLWEsk(vim⋅sk+e⋅sk)
把它们重排为 RGSW 密文即可。
Prime Cyclotomic Rings
[DKM+24] 使用 R r e g = Z Q [ X ] / ( Φ q ( X ) ) R_{reg} = \mathbb Z_Q[X]/(\Phi_q(X)) Rreg=ZQ[X]/(Φq(X)) 作为寄存器的空间,其中 q q q 是素数。对于整数 m ∈ Z q m \in \mathbb Z_q m∈Zq,将它编码为 X m ∈ R r e g X^m \in R_{reg} Xm∈Rreg 加密为 RLWE’ 或者 RGSW 密文。
需要重新考虑这种 RGSW 密文上外积的噪声增长情况,

对于二的幂次分圆环,噪声为 σ ⊙ 2 = B 2 d B N σ i n p u t 2 / 12 \sigma^2_\odot = B^2d_BN\sigma_{input}^2/12 σ⊙2=B2dBNσinput2/12,因此素数次分圆环上的噪声仅增长了 2 2 2 因子,可以接受。
Decryption
[DKM+24] 使用 [MS18] 的框架,主要的区别就是在同态解密步骤使用了素数次分圆环,利用 Galois 自同构实现数乘,利用 Incomplete NTT 实现 IDFT。
令 d d d 是二的幂次,定义 R i n = Z q [ X ] / ( Φ d ( X ) ) R_{in} = \mathbb Z_q[X]/(\Phi_d(X)) Rin=Zq[X]/(Φd(X)),作为打包密文的空间。给定 ϕ ( d ) \phi(d) ϕ(d) 个 LWE 密文,使用 Ring Packing(就是 column method Pub-KS)将它们转化为系数打包的 RLWE 密文 ( b , a ) ∈ R i n 2 (b,a) \in R_{in}^2 (b,a)∈Rin2,私钥是 z ∈ R i n z \in R_{in} z∈Rin

对于卷积环,将它的 FFT/NTT 称为 standard/cyclic FFT。对于分圆环,将它的 FFT/NTT 称为 primitive/cyclotomic FFT。
- 对于寄存器本身,基本运算是在 R r e g R_{reg} Rreg 上执行的,需要把 Z Q [ X ] / ( 1 + X + X 2 + ⋯ + X q − 1 ) \mathbb Z_Q[X]/(1+X+X^2+\cdots+X^{q-1}) ZQ[X]/(1+X+X2+⋯+Xq−1) 做 primitive FFT,不过我们直接将寄存器视为一个黑盒,可以不关心这个的实现。
- 对于打包密文,基本运算是在 R i n R_{in} Rin 上执行的,需要对反卷积环 Z q [ X ] / ( X ϕ ( d ) + 1 ) \mathbb Z_q[X]/(X^{\phi(d)}+1) Zq[X]/(Xϕ(d)+1) 做 primitive FFT,可以先执行相同长度的 cyclic FFT,然后乘以一些 twist factor 即可。这些运算是利用大量的寄存器完成的。
为了快速计算 b + a ⋅ z ∈ R i n b + a \cdot z \in R_{in} b+a⋅z∈Rin,[DKM+24] 采用了 partial primitive FFT(PFT),因为噪声增长是和递归分解的深度呈指数的,只能做常数深度的分解。分解是:
Z q [ X ] / ( X ϕ ( d ) + 1 ) ≅ ∏ i = 0 ϕ ( d ) / k − 1 Z q [ X ] / ( X k − ζ i ) \mathbb Z_q[X]/(X^{\phi(d)}+1) \cong \prod_{i=0}^{\phi(d)/k-1} \mathbb Z_q[X]/(X^k - \zeta_i) Zq[X]/(Xϕ(d)+1)≅i=0∏ϕ(d)/k−1Zq[X]/(Xk−ζi)
其中 ζ i \zeta_i ζi 是所有的 d / k d/k d/k 次本原单位根。由于 DFT 和 IDFT 的表达式之间有个缩放因子,自举过程中 DFT 是明文下的,IDFT 是密文下的。为了减少同态开销,[DKM+24] 将这个缩放因子从 IDFT 移动到了 DFT。于是,给定环元素 a ∈ R i n a \in R_{in} a∈Rin,执行 PFT 获得:
a ~ i = [ ( ϕ ( d ) / k ) − 1 ] q ⋅ a ( m o d X k − ζ i ) \tilde a_i = [(\phi(d)/k)^{-1}]_q \cdot a \pmod{X^k-\zeta_i} a~i=[(ϕ(d)/k)−1]q⋅a(modXk−ζi)
对于私钥 z ∈ R i n z \in R_{in} z∈Rin,也将它做 PFT 获得 ϕ ( d ) / k \phi(d)/k ϕ(d)/k 个多项式 { z ~ i } \{\tilde z_i\} {z~i},将它们的系数 z ~ i ( j ) ∈ Z q \tilde z_i^{(j)} \in \mathbb Z_q z~i(j)∈Zq 加密为:
R G S W ( X z ~ i ( j ) ) , 0 ≤ i < ϕ ( d ) / k , 0 ≤ j < k RGSW(X^{\tilde z_i^{(j)}}), 0 \le i < \phi(d)/k, 0\le j< k RGSW(Xz~i(j)),0≤i<ϕ(d)/k,0≤j<k
对于某个小环 Z q [ X ] / ( X k − ζ i ) \mathbb Z_q[X]/(X^k - \zeta_i) Zq[X]/(Xk−ζi),按照 Schoolbook 方式计算 v = a ~ i ⋅ z ~ i v = \tilde a_i \cdot \tilde z_i v=a~i⋅z~i,
v j = ∑ l = 0 j z ~ i ( l ) a ~ i ( j − l ) + ζ i ⋅ ∑ l = j + 1 l − 1 z ~ i ( l ) a ~ i ( k + j − l ) \begin{aligned} v_j = \sum_{l=0}^j\tilde z_i^{(l)}\tilde a_i^{(j-l)} + \zeta_i\cdot\sum_{l=j+1}^{l-1}\tilde z_i^{(l)}\tilde a_i^{(k+j-l)} \end{aligned} vj=l=0∑jz~i(l)a~i(j−l)+ζi⋅l=j+1∑l−1z~i(l)a~i(k+j−l)
由于 a ~ i \tilde a_i a~i 是明文,因此可以把 v j v_j vj 视为密文向量 z ⃗ = ( z ~ i ( 0 ) , ⋯ , z ~ i ( k − 1 ) ) \vec z = (\tilde z_i^{(0)}, \cdots, \tilde z_i^{(k-1)}) z=(z~i(0),⋯,z~i(k−1)) 和明文向量 c ⃗ = ( a ~ i ( j ) , a ~ i ( j − 1 ) , ⋯ , a ~ i ( 0 ) , ζ i a ~ i ( k − 1 ) , ζ i a ~ i ( k − 2 ) , ⋯ , ζ i a ~ i ( j + 1 ) ) \vec c = (\tilde a_i^{(j)}, \tilde a_i^{(j-1)},\cdots, \tilde a_i^{(0)}, \zeta_i\tilde a_i^{(k-1)}, \zeta_i\tilde a_i^{(k-2)}, \cdots, \zeta_i\tilde a_i^{(j+1)}) c=(a~i(j),a~i(j−1),⋯,a~i(0),ζia~i(k−1),ζia~i(k−2),⋯,ζia~i(j+1)) 的内积。毕竟密文上的数乘是相对明文数乘更贵的。[DKM+24] 使用 RLWE’ 寄存器(编码在指数上,线性同态),同态数乘使用 Galois 自同构(输入输出都是 RLWE’ 密文),同态加法使用 RGSW 外积(输入 RGSW 和 RLWE’ 密文,输出 RLWE’ 密文)。为了减少 RLWE’ to RGSW 转换,可以使用如下的方式计算 z ⃗ , c ⃗ \vec z, \vec c z,c 的内积(假设 c i ∈ Z q c_i \in \mathbb Z_q ci∈Zq 全都非零、可逆,如果是零则简单删除):
v j = ( ( ⋯ ( z 0 c 0 c 1 − 1 + z 1 ) c 1 c 2 − 1 + ⋯ ) z k − 2 z k − 1 − 1 + z k − 1 ) c k − 1 v_j = ((\cdots(z_0c_0c_1^{-1} + z_1)c_1c_2^{-1} +\cdots)z_{k-2}z_{k-1}^{-1} + z_{k-1})c_{k-1} vj=((⋯(z0c0c1−1+z1)c1c2−1+⋯)zk−2zk−1−1+zk−1)ck−1
这样整个过程都只需要 RLWE’ 寄存器,并不需要转换到 RGSW 密文。
算法是:

现在,我们计算出了 v ~ i = a ~ i ⋅ z ~ i ∈ Z q [ X ] / ( X k − ζ i ) \tilde v_i = \tilde a_i \cdot \tilde z_i \in \mathbb Z_q[X]/(X^k-\zeta_i) v~i=a~i⋅z~i∈Zq[X]/(Xk−ζi),它的系数加密在 k k k 个 RLWE’ 寄存器内。重复 ϕ ( d ) / k \phi(d)/k ϕ(d)/k 次,计算出所有的 { v ~ i } \{\tilde v_i\} {v~i},接下来需要执行 Homomorphic IPFT 恢复出 v = a ⋅ s v=a \cdot s v=a⋅s 的各个系数。
INTT
这个过程的思想很简单,就是直接用 RLWE’ 寄存器的线性同态,执行 Inverse PFT 即可。
根据环同构:
Z q [ X ] / ( X ϕ ( d ) + 1 ) ≅ ( Z q [ Y ] / ( Y ϕ ( d ) / k + 1 ) ) [ X ] / ( X k − Y ) ≅ Z q ϕ ( d ) / k [ X ] / ( X k − Y ) \begin{aligned} \mathbb Z_q[X]/(X^{\phi(d)}+1) &\cong (\mathbb Z_q[Y]/(Y^{\phi(d)/k}+1))[X]/(X^k-Y)\\ &\cong \mathbb Z_q^{\phi(d)/k}[X]/(X^k-Y) \end{aligned} Zq[X]/(Xϕ(d)+1)≅(Zq[Y]/(Yϕ(d)/k+1))[X]/(Xk−Y)≅Zqϕ(d)/k[X]/(Xk−Y)
其中 Z q ϕ ( d ) / k \mathbb Z_q^{\phi(d)/k} Zqϕ(d)/k 是以 coeff-wise 方式运算的。Incomplete cyclotomic NTT 可以写成多个 Complete cyclotomic NTT 的并行。
根据环同构:
Z q [ Y ] / ( Y ϕ ( d ) / k + 1 ) ≅ Z q [ Z ] / ( Z N − 1 ) \mathbb Z_q[Y]/(Y^{\phi(d)/k}+1) \cong \mathbb Z_q[Z]/(Z^{N}-1) Zq[Y]/(Yϕ(d)/k+1)≅Zq[Z]/(ZN−1)
其中 Y = Z ζ Y = Z\zeta Y=Zζ,这里 ζ \zeta ζ 是 d / k d/k d/k 次本原单位根,而 Z Z Z 是 N = ϕ ( d ) / k N=\phi(d)/k N=ϕ(d)/k 次本原单位根。Complete cyclotomic NTT 可以写成 Complete cyclic NTT,然后再扭曲。

根据环同构:
Z q [ Z ] / ( Z R − ζ N j ) ≅ ∏ i = 0 r − 1 Z q [ Z ] / ( Z R / r − ζ N j r − 1 + i N / r ) \mathbb Z_q[Z]/(Z^{R}-\zeta_N^j) \cong \prod_{i=0}^{r-1}\mathbb Z_q[Z]/(Z^{R/r}-\zeta_N^{jr^{-1}+iN/r}) Zq[Z]/(ZR−ζNj)≅i=0∏r−1Zq[Z]/(ZR/r−ζNjr−1+iN/r)
以及映射 Z R / r → ζ N j r − 1 + i N / r Z^{R/r} \to \zeta_N^{jr^{-1}+iN/r} ZR/r→ζNjr−1+iN/r,
∑ k = 0 R − 1 a k Z k → ∑ l = 0 R / r − 1 ( ∑ k = 0 r − 1 a l + k R / r ( ζ N j r − 1 + i N / r ) k ) ⋅ Z l \sum_{k=0}^{R-1} a_kZ^k \to \sum_{l=0}^{R/r-1} \left(\sum_{k=0}^{r-1} a_{l+kR/r}(\zeta_N^{jr^{-1}+iN/r})^k\right)\cdot Z^l k=0∑R−1akZk→l=0∑R/r−1(k=0∑r−1al+kR/r(ζNjr−1+iN/r)k)⋅Zl
其中 ζ N j r − 1 + i N / r \zeta_N^{jr^{-1}+iN/r} ζNjr−1+iN/r 是所有的 ζ N j \zeta_N^j ζNj 的 r r r 次根,这里 r ∣ R ∣ N r \mid R \mid N r∣R∣N 是当前层的 radix 设置。Complete cyclic NTT 的每一层分解都是若干个关于某些单位根的多项式求值。


其中的 { r i } 0 ≤ i < l \{r_i\}_{0 \le i < l} {ri}0≤i<l 是每一层分解的 radix,递归深度 l l l 是常数。由于自举的最终结果是单个 RLWE 密文,因此它的各个系数只需要被加密在单个 RLWE 寄存器里,所以最后一层使用外积 Q / 4 ⊙ c t i Q/4 \odot ct_i Q/4⊙cti 把寄存器 R L W E ′ ( X v ) RLWE'(X^v) RLWE′(Xv) 转化为 R L W E ( Q / 4 ⋅ X v ) RLWE(Q/4 \cdot X^v) RLWE(Q/4⋅Xv) 密文,这里的 4 4 4 是原始 FHEW 的明文模数。
依次执行 v ~ i = a ~ i ⋅ s ~ i \tilde v_i = \tilde a_i \cdot \tilde s_i v~i=a~i⋅s~i 以及上述的 P F T − 1 ( { v ~ i } ) PFT^{-1}(\{\tilde v_i\}) PFT−1({v~i}),最终获得各个系数的密文 R L W E ( Q / 4 ⋅ X ( a ⋅ s ) j ) RLWE(Q/4 \cdot X^{(a \cdot s)_j}) RLWE(Q/4⋅X(a⋅s)j),然后再分别乘以 X b j X^{b_j} Xbj 得到 ϕ ( d ) \phi(d) ϕ(d) 个密文 R L W E ( Q / 4 ⋅ X ( b + a ⋅ s ) j ) RLWE(Q/4 \cdot X^{(b+a \cdot s)_j}) RLWE(Q/4⋅X(b+a⋅s)j)
msbExtract
现在 ( b , a ) ∈ R i n 2 (b,a) \in R_{in}^2 (b,a)∈Rin2 相位的各个系数 c = ( b + a ⋅ s ) i ∈ Z q c=(b+a \cdot s)_i \in \mathbb Z_q c=(b+a⋅s)i∈Zq 分别加密在 RLWE 密文 ( b ^ , a ^ ) ∈ R r e g 2 (\hat b, \hat a) \in R_{reg}^2 (b^,a^)∈Rreg2 相位的指数上,简记为 m ( X ) = Q / 4 ⋅ X c ∈ R r e g m(X) = Q/4 \cdot X^{c} \in R_{reg} m(X)=Q/4⋅Xc∈Rreg,私钥是 s ^ ∈ R r e g \hat s \in R_{reg} s^∈Rreg
由于 Φ q ( X ) = 1 + X + ⋯ + X q − 1 \Phi_q(X) = 1+X+\cdots+X^{q-1} Φq(X)=1+X+⋯+Xq−1,因此有 X q − 1 ≡ − 1 − X − ⋯ − X q − 2 X^{q-1} \equiv -1-X-\cdots-X^{q-2} Xq−1≡−1−X−⋯−Xq−2 以及 X q = 1 X^q=1 Xq=1,那么
m i + e i = b ^ i + ∑ j = 0 i a ^ i − j s ^ j + ∑ j = i + 2 q − 2 a ^ q + i − j s ^ j − ∑ j = 1 q − 2 a ^ q − 1 − j s ^ j = b ^ i + ⟨ ( a ^ i , a ^ i − 1 − a ^ q − 2 , a ^ i − 2 − a ^ q − 3 , ⋯ , a ^ 0 − a ^ q − i − 1 , 0 − a ^ q − i − 2 , a ^ q − 2 − a ^ q − i − 3 , ⋯ , a ^ i + 2 − a ^ 1 ) , ( s ^ 0 , ⋯ , s ^ q − 2 ) ⟩ \begin{aligned} m_i + e_i &= \hat b_i + \sum_{j=0}^{i}\hat a_{i-j}\hat s_j + \sum_{j=i+2}^{q-2}\hat a_{q+i-j}\hat s_j - \sum_{j=1}^{q-2} \hat a_{q-1-j}\hat s_j\\ &= \hat b_i + \langle(\hat a_i, \hat a_{i-1}-\hat a_{q-2}, \hat a_{i-2}-\hat a_{q-3}, \cdots, \\ &\,\,\,\,\,\,\,\, \hat a_{0}-\hat a_{q-i-1}, 0-\hat a_{q-i-2}, \hat a_{q-2}-\hat a_{q-i-3}, \cdots, \hat a_{i+2}-\hat a_{1}), (\hat s_0,\cdots,\hat s_{q-2})\rangle \end{aligned} mi+ei=b^i+j=0∑ia^i−js^j+j=i+2∑q−2a^q+i−js^j−j=1∑q−2a^q−1−js^j=b^i+⟨(a^i,a^i−1−a^q−2,a^i−2−a^q−3,⋯,a^0−a^q−i−1,0−a^q−i−2,a^q−2−a^q−i−3,⋯,a^i+2−a^1),(s^0,⋯,s^q−2)⟩
因此 ( b i , a ⃗ i : = ( a ^ i , a ^ i − 1 − a ^ q − 2 , a ^ i − 2 − a ^ q − 3 , ⋯ , a ^ 0 − a ^ q − i − 1 , 0 − a ^ q − i − 2 , a ^ q − 2 − a ^ q − i − 3 , ⋯ , a ^ i + 2 − a ^ 1 ) ) ∈ Z Q q (b_i,\vec a_i := (\hat a_i, \hat a_{i-1}-\hat a_{q-2}, \hat a_{i-2}-\hat a_{q-3}, \cdots, \hat a_{0}-\hat a_{q-i-1}, 0-\hat a_{q-i-2}, \hat a_{q-2}-\hat a_{q-i-3}, \cdots, \hat a_{i+2}-\hat a_{1})) \in \mathbb Z_Q^{q} (bi,ai:=(a^i,a^i−1−a^q−2,a^i−2−a^q−3,⋯,a^0−a^q−i−1,0−a^q−i−2,a^q−2−a^q−i−3,⋯,a^i+2−a^1))∈ZQq 就是 m ( X ) m(X) m(X) 系数 m i m_i mi 的密文,私钥是 s ⃗ : = ( s ^ 0 , ⋯ , s ^ q − 2 ) \vec s := (\hat s_0,\cdots,\hat s_{q-2}) s:=(s^0,⋯,s^q−2),噪声是 e i e_i ei
- 如果 c = i c=i c=i,那么 m i = Q / 4 m_i = Q/4 mi=Q/4
- 如果 c = q − 1 c=q-1 c=q−1,那么 m i = − Q / 4 m_i=-Q/4 mi=−Q/4
- 对于其他的 c c c,都是 m i = 0 m_i=0 mi=0
为了提取出系数 c = q / 2 ⋅ μ + e c=q/2 \cdot \mu + e c=q/2⋅μ+e 所编码的消息 μ ∈ { 0 , 1 } \mu \in \{0,1\} μ∈{0,1},由于噪声范围 [ − q / 4 , q / 4 ) [-q/4, q/4) [−q/4,q/4),因此 μ = 1 ⟺ c ∈ ( q / 4 , 3 q / 4 ) \mu=1 \iff c \in (q/4,3q/4) μ=1⟺c∈(q/4,3q/4),那么把这个区间的 LWE 密文加起来即可(注意 m ( X ) m(X) m(X) 恰是 one-hot 向量)。
Counting
以外积为单位,各个步骤的复杂度是:

各个步骤的噪声增长是:

安全强度 λ = O ( n ) \lambda = O(n) λ=O(n),模数 Q = p o l y ( n ) Q=poly(n) Q=poly(n),打包数量 ϕ ( d ) = O ( n ) \phi(d)=O(n) ϕ(d)=O(n),Gadget 分解长度 d B = log B Q d_B = \log_B Q dB=logBQ。由于环元素和 RLWE’ 密文外积的噪声是 σ ⊙ 2 = B 2 d B q σ i n p u t 2 / 6 = O ( n ) ⋅ σ i n p u t 2 \sigma^2_\odot = B^2d_Bq\sigma_{input}^2/6 = O(n)\cdot\sigma_{input}^2 σ⊙2=B2dBqσinput2/6=O(n)⋅σinput2,上述的 σ ⊙ , a u t 2 , σ ⊙ , e v a l 2 , σ ⊙ , R G S W 2 \sigma_{\odot,aut}^2, \sigma_{\odot,eval}^2, \sigma_{\odot,RGSW}^2 σ⊙,aut2,σ⊙,eval2,σ⊙,RGSW2 分别是 RLWE’ 自同构密钥、RLWE‘ to RGSW 切换密钥、RGSW 自举密钥的方差取代 σ i n p u t 2 \sigma_{input}^2 σinput2 之后的值。假如 PFT 的迭代深度是 l l l 层,那么最终的方差是 O ( n l ) ⋅ σ a u t , e v a l , R G S W 2 O(n^l) \cdot \sigma_{aut,eval,RGSW}^2 O(nl)⋅σaut,eval,RGSW2,是关于 l l l 指数级的。由于 Q Q Q 是多项式规模的,因此 l l l 必须是较小的常数。
对于常数深度 l l l,设置 k = r = ϕ ( d ) 1 / l k=r=\phi(d)^{1/l} k=r=ϕ(d)1/l,这里 k k k 是分解后的小多项式长度, r r r 是各层分解的 radix 大小。那么,总的复杂度是 O ( l n 1 + 1 / l log n ) O(ln^{1+1/l}\log n) O(ln1+1/llogn) 次环元素和 RLWE’ 的外积,均摊复杂度是 O ( l n 1 / l log n ) O(ln^{1/l}\log n) O(ln1/llogn) 次外积。
相关文章:

Amortized bootstrapping via Automorphisms
参考文献: [MS18] Micciancio D, Sorrell J. Ring packing and amortized FHEW bootstrapping. ICALP 2018: 100:1-100:14.[GPV23] Guimares A, Pereira H V L, Van Leeuwen B. Amortized bootstrapping revisited: Simpler, asymptotically-faster, implemented. …...

【人工智能】ChatGPT基本工作原理
ChatGPT 是由 OpenAI 开发的一种基于深度学习技术的自然语言处理模型,它使用了名为 GPT(Generative Pre-trained Transformer)的架构。GPT 模型是一种基于 Transformer 架构的预训练语言模型,它通过大量的文本数据进行预训练&…...
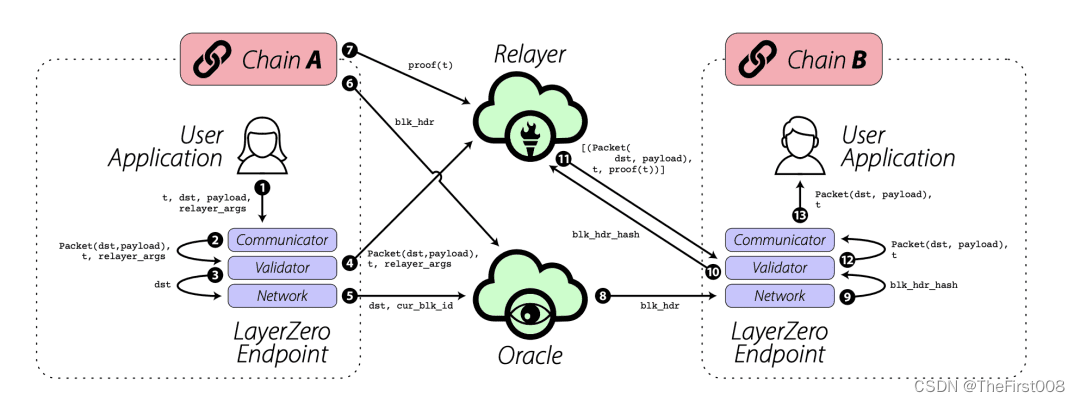
The First项目报告:Stargate Finance重塑跨链金融的未来
Stargate Finance是一个基于LayerZero协议的去中心化金融平台,自2022年3月由LayerZero Labs创建以来,一直致力于为不同区块链之间的资产转移提供高效、低成本的解决方案。凭借其独特的跨链技术和丰富的DeFi服务,Stargate Finance已成为连接不…...

Python魔法之旅-魔法方法(22)
目录 一、概述 1、定义 2、作用 二、应用场景 1、构造和析构 2、操作符重载 3、字符串和表示 4、容器管理 5、可调用对象 6、上下文管理 7、属性访问和描述符 8、迭代器和生成器 9、数值类型 10、复制和序列化 11、自定义元类行为 12、自定义类行为 13、类型检…...
)
公司面试题总结(三)
13.说说你对 BOM 的理解,常见的 BOM 对象你了解哪些? BOM (Browser Object Model),浏览器对象模型, ⚫ 提供了独立于内容与浏览器窗口进行交互的对象 ⚫ 其作用就是跟浏览器做一些交互效果 ⚫ 比如如何进行页面的后退&…...
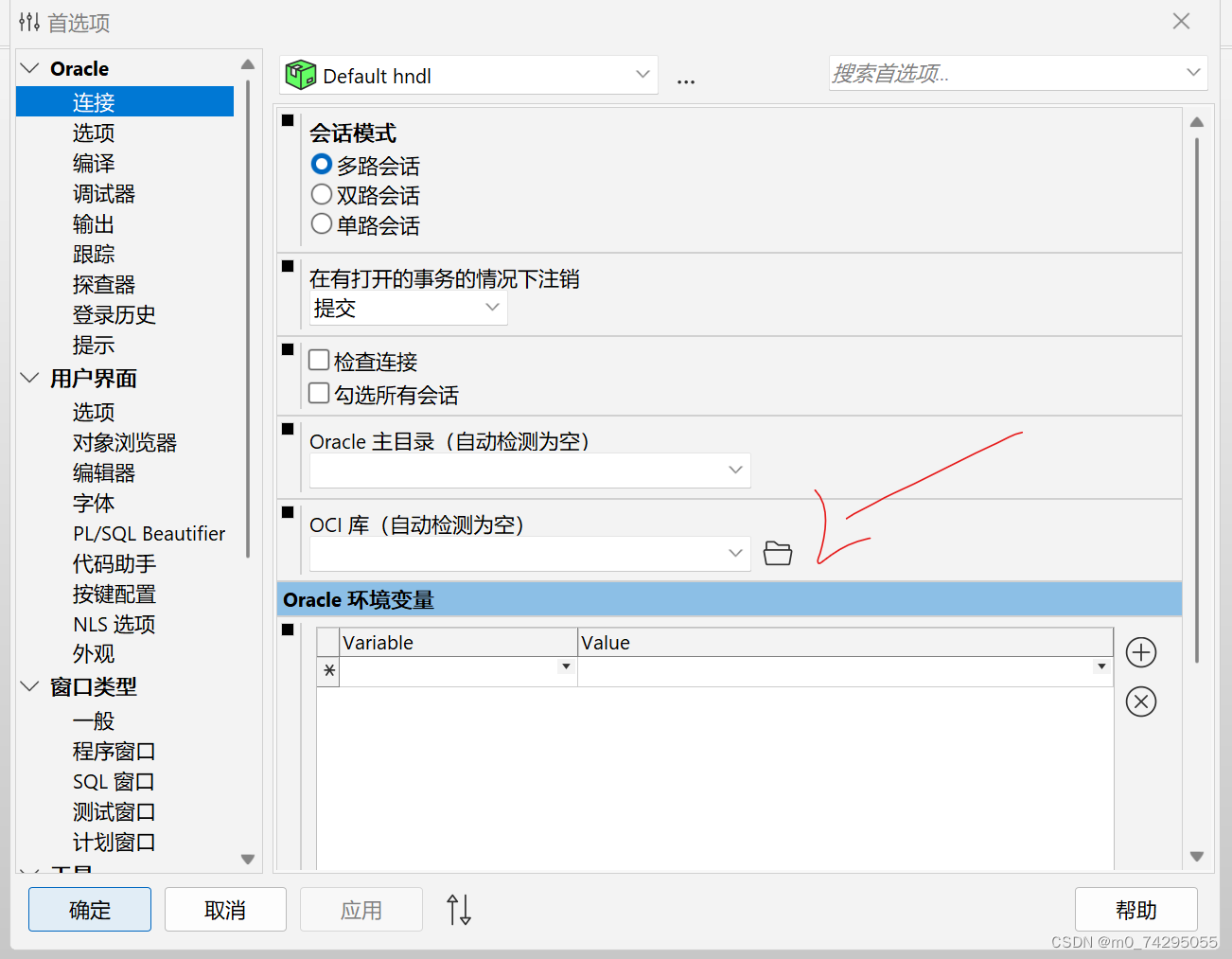
PLSQL 报错 could not locate oci.dll
0、确保PLSQL已激活。 1、在PLSQL安装包内搜索oci.dll,如果没有搜到需要下载 链接:https://pan.baidu.com/s/1HOfKAEFfuAGYACjfcwqJ1g 提取码:6evh 2、打开PLSQL,设置oci.dll的路径 ps:PLSQL安装包 链接ÿ…...

【方案+源码】智慧园区建设方案
智慧园区一体化运营管理平台建设方案旨在通过集成先进的信息技术,实现园区的智能化、高效化、绿色化管理。该平台整合了物联网、大数据、云计算等技术,为园区提供全方位、一体化的运营服务。 方案包括智能监控、能源管理、安防系统、停车管理、物业管理等…...

Java操作数据库 —— JDBC ① 基础篇
我走我的路,有人拦也走,没人陪也走 —— 24.6.7 JDBC JDBC就是使用Java语言操作关系型数据库的一套API 一、JDBC简介 JDBC 概念 JDBC 就是使用Java语言操作关系型数据库的一套API 全称:(Java DataBase Connectivity)意为Java 数据库连接 JDBC 本质: ①…...

webpack和vite区别
一、Webpack 1. 概述 Webpack 是一个模块打包工具,它会递归地构建依赖关系图,并将所有模块打包成一个或多个bundle(包)。 2. 特点 配置灵活:Webpack提供了高度可定制的配置文件,可以根据项目需求进行各…...

FL Studio21永久免费破解中文版下载,让我这个音乐制作爱好者如获至宝!
FL Studio21永久免费破解中文版下载,让我这个音乐制作爱好者如获至宝!🎶 这款软件功能强大,操作简单易上手。我可以轻松地创作出各种风格的音乐作品。无论是流行、摇滚还是电子音乐,都能轻松驾驭。🎧 使用F…...
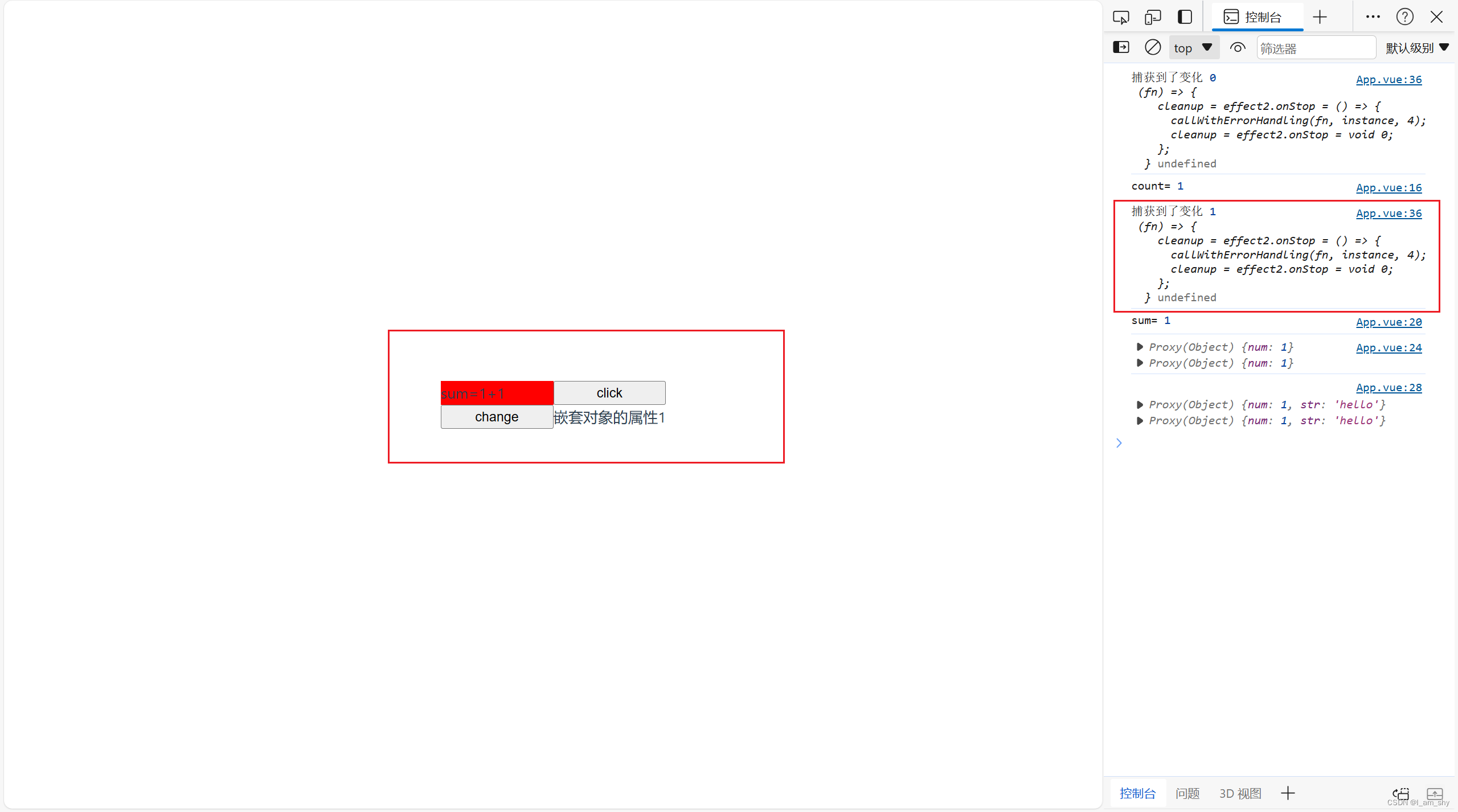
vue3 监听器,组合式API的watch用法
watch函数 在组合式 API 中,我们可以使用 watch 函数在每次响应式状态发生变化时触发回调函数 watch(ref,callback(newValue,oldValue),option:{}) ref:被监听的响应式量,可以是一个 ref (包括计算属性)、一个响应式…...

苹果WWDC开幕发布AI大模型,股价却跌近2%
KlipC报道:北京时间6月11日凌晨,苹果一年一度的“全球开发者大会”(WWDC)开幕。会上,先后介绍了iOS 18、iPadOS 18、watchOS 11等系统的更新,同时还展示了多个AI功能。宣布与OpenAI构建合作伙伴关系。然而&…...

C++ 11 【可变参数模板】【lambda】
💓博主CSDN主页:麻辣韭菜💓 ⏩专栏分类:C修炼之路⏪ 🚚代码仓库:C高阶🚚 🌹关注我🫵带你学习更多C知识 🔝🔝 目录 前言 一、新的类功能 1.1默认成员函数—…...

c 宏应用举例
1.概要 #include <iostream> //变量可以直接使用 #define fun() a 100; //用变量计算可以 #define fun2(a) a*2; //用变量替换可以 #define fun3(a) d[a] a; //##链接的作用,一般用于链接变量名 #define fun4(type,name) type name##_s 4; //#的作用是转换…...

微信公众号(公众平台) 和 微信开放平台的scope的差异
微信公众号(公众平台) 和 微信开放平台 是两码事。 公众号(公众平台)获取的scope只包括两种:snsapi_base 和snsapi_userinfo,前者是静默获取,用户无感知;后者是需要用户确认同意的。…...

基于pytorch实现的DenseUnet医学图像分割(腹部多脏器)
1、前言 本章将介绍将densenet的主干网络引入unet中 官方实现的代码:kits19-challenge/network at master nitsaick/kits19-challenge (github.com) 本章实现的项目目录如下: 主要代码有train、evaluate、predict脚本 2、代码介绍 数据预处理脚本 数据…...

富格林:正规策划实现安全做单
富格林悉知,在投资理财的过程中,最重要的是控制风险实现安全做单避免损失。但是市场客观因素带来的风险并不能完全避免,因此投资者需要采取一些正规技能来减低风险投资风险实现安全做单。接下来就由富格林给大家分享一些实现安全做单的正规方…...

02. 异常捕捉和处理
检索特定内容的邮件,当检索失败,就会在终端输出“获取不了值” try: #代码块A except: #代码B 试一下运行代码A,当代码A报错时,执行代码B 这是main_exe.py文件中的内容 略过 #今天 for job_name,end_time in zip(bji.job_inf…...
Oracle和mysql中插入时间字段
例如有id 和 times两个字段 Oracle insert into xxx values|(1,sysdate) mysql insert into xxx values(1,now()) 在 MySQL 中,SYSDATE() 函数也是可用的,它与 NOW() 类似,但略有不同: NOW…...

注册小程序
每个小程序都需要在 app.js 中调用 App 方法注册小程序实例,绑定生命周期回调函数、错误监听和页面不存在监听函数等。 详细的参数含义和使用请参考 App 参考文档 。 整个小程序只有一个 App 实例,是全部页面共享的。开发者可以通过 getApp 方法获取到全…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

智能仓储的未来:自动化、AI与数据分析如何重塑物流中心
当仓库学会“思考”,物流的终极形态正在诞生 想象这样的场景: 凌晨3点,某物流中心灯火通明却空无一人。AGV机器人集群根据实时订单动态规划路径;AI视觉系统在0.1秒内扫描包裹信息;数字孪生平台正模拟次日峰值流量压力…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

[大语言模型]在个人电脑上部署ollama 并进行管理,最后配置AI程序开发助手.
ollama官网: 下载 https://ollama.com/ 安装 查看可以使用的模型 https://ollama.com/search 例如 https://ollama.com/library/deepseek-r1/tags # deepseek-r1:7bollama pull deepseek-r1:7b改token数量为409622 16384 ollama命令说明 ollama serve #:…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...
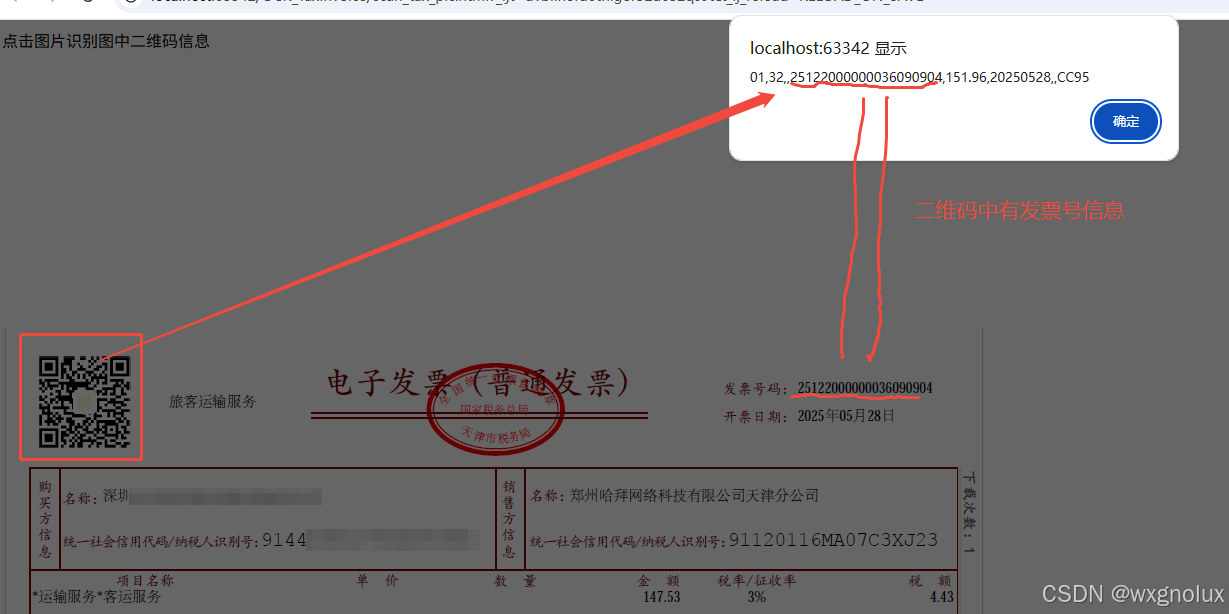
网页端 js 读取发票里的二维码信息(图片和PDF格式)
起因 为了实现在报销流程中,发票不能重用的限制,发票上传后,希望能读出发票号,并记录发票号已用,下次不再可用于报销。 基于上面的需求,研究了OCR 的方式和读PDF的方式,实际是可行的ÿ…...
