第十九节:暴力递归到动态规划
一 动画规划的概念 优化出现重复解的递归
一旦写出递归来,改动态规划就很快
尝试策略和状态转移方程是一码事
学会尝试是攻克动态规划最本质的能力
如果你发现你有重复调用的过程,动态规划在算过一次之后把答案记下来,下回在越到重复调用过程就直接调
做题思路 一定要从尝试入手
动态规划的套路从尝试出发,从尝试递归出发,然后在改动态规划的时候第一步找到base的情况填上相应位置的数,然后根据下一步的条件推出其他位置的数;
二 给定四个参数 N、M、K、P,返回方法数,机器人必须走 K 步
2.1描述
假设有排成一行的N个位置,记为1~N,N 一定大于或等于 2
开始时机器人在其中的M位置上(M 一定是 1~N 中的一个)
如果机器人来到1位置,那么下一步只能往右来到2位置;
如果机器人来到N位置,那么下一步只能往左来到 N-1 位置;
如果机器人来到中间位置,那么下一步可以往左走或者往右走;
规定机器人必须走 K 步,最终能来到P位置(P也是1~N中的一个)的方法有多少种
给定四个参数 N、M、K、P,返回方法数。
2.2 分析
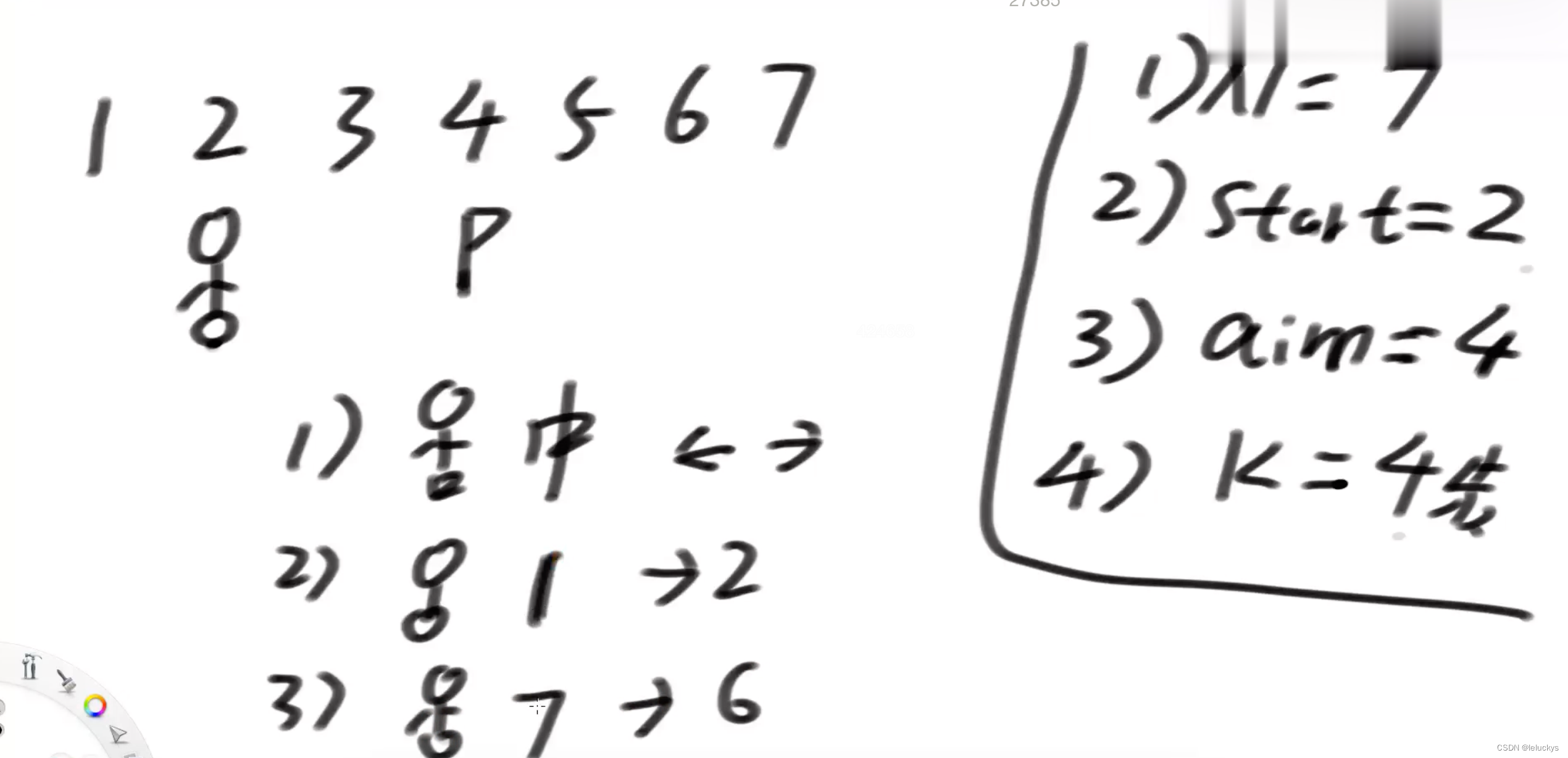
2.3 代码
// 机器人当前来到的位置是cur,// 机器人还有rest步需要去走,// 最终的目标是aim,// 有哪些位置?1~N// 返回:机器人从cur出发,走过rest步之后,最终停在aim的方法数,是多少?public static int process1(int cur, int rest, int aim, int N) {if (rest == 0) { // 如果已经不需要走了,走完了!return cur == aim ? 1 : 0;}// (cur, rest)if (cur == 1) { // 1 -> 2return process1(2, rest - 1, aim, N);}// (cur, rest)if (cur == N) { // N-1 <- Nreturn process1(N - 1, rest - 1, aim, N);}// (cur, rest)return process1(cur - 1, rest - 1, aim, N) + process1(cur + 1, rest - 1, aim, N);}
2.4 优化 递归改动态规划 一 有重复解的递归是可以优化的
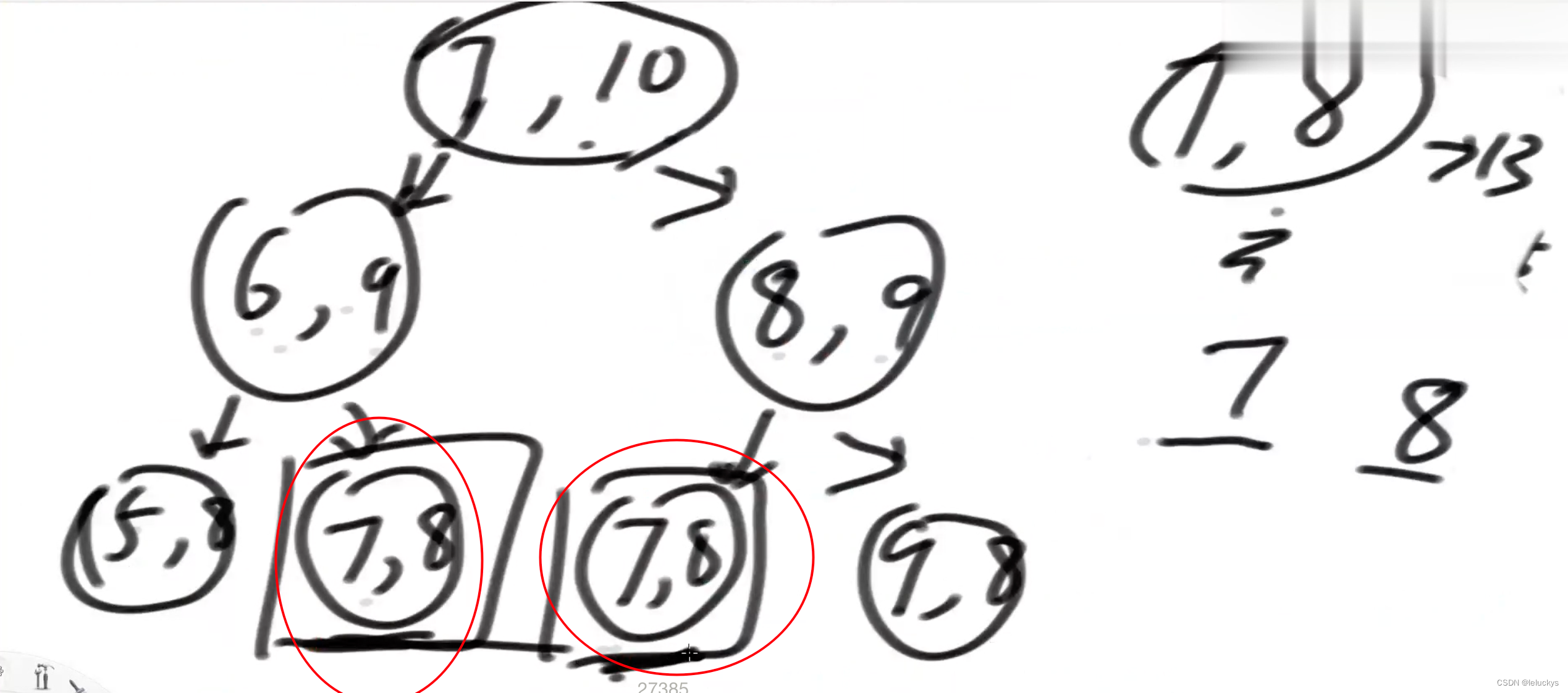
上面递归的过程中出现了重复的值,采用缓存法记录已经走过的路就不用再走了,一个字问题保证只算一次
public static int ways2(int N, int start, int aim, int K) {if (N < 2 || start < 1 || start > N || aim < 1 || aim > N || K < 1) {return -1;}int[][] dp = new int[N + 1][K + 1];for (int i = 0; i <= N; i++) {for (int j = 0; j <= K; j++) {dp[i][j] = -1;}}// dp就是缓存表// dp[cur][rest] == -1 -> process1(cur, rest)之前没算过!// dp[cur][rest] != -1 -> process1(cur, rest)之前算过!返回值,dp[cur][rest]// N+1 * K+1return process2(start, K, aim, N, dp);}// cur 范: 1 ~ N// rest 范:0 ~ Kpublic static int process2(int cur, int rest, int aim, int N, int[][] dp) {if (dp[cur][rest] != -1) {return dp[cur][rest];}// 之前没算过!int ans = 0;if (rest == 0) {ans = cur == aim ? 1 : 0;} else if (cur == 1) {ans = process2(2, rest - 1, aim, N, dp);} else if (cur == N) {ans = process2(N - 1, rest - 1, aim, N, dp);} else {ans = process2(cur - 1, rest - 1, aim, N, dp) + process2(cur + 1, rest - 1, aim, N, dp);}dp[cur][rest] = ans;return ans;}
三 给定一个整型数组arr,代表数值不同的纸牌排成一条线
范围模型 玩家博弈问题
3.1 描述
给定一个整型数组arr,代表数值不同的纸牌排成一条线
玩家A和玩家B依次拿走每张纸牌
规定玩家A先拿,玩家B后拿
但是每个玩家每次只能拿走最左或最右的纸牌
玩家A和玩家B都绝顶聪明
请返回最后获胜者的分数。
3.2分析
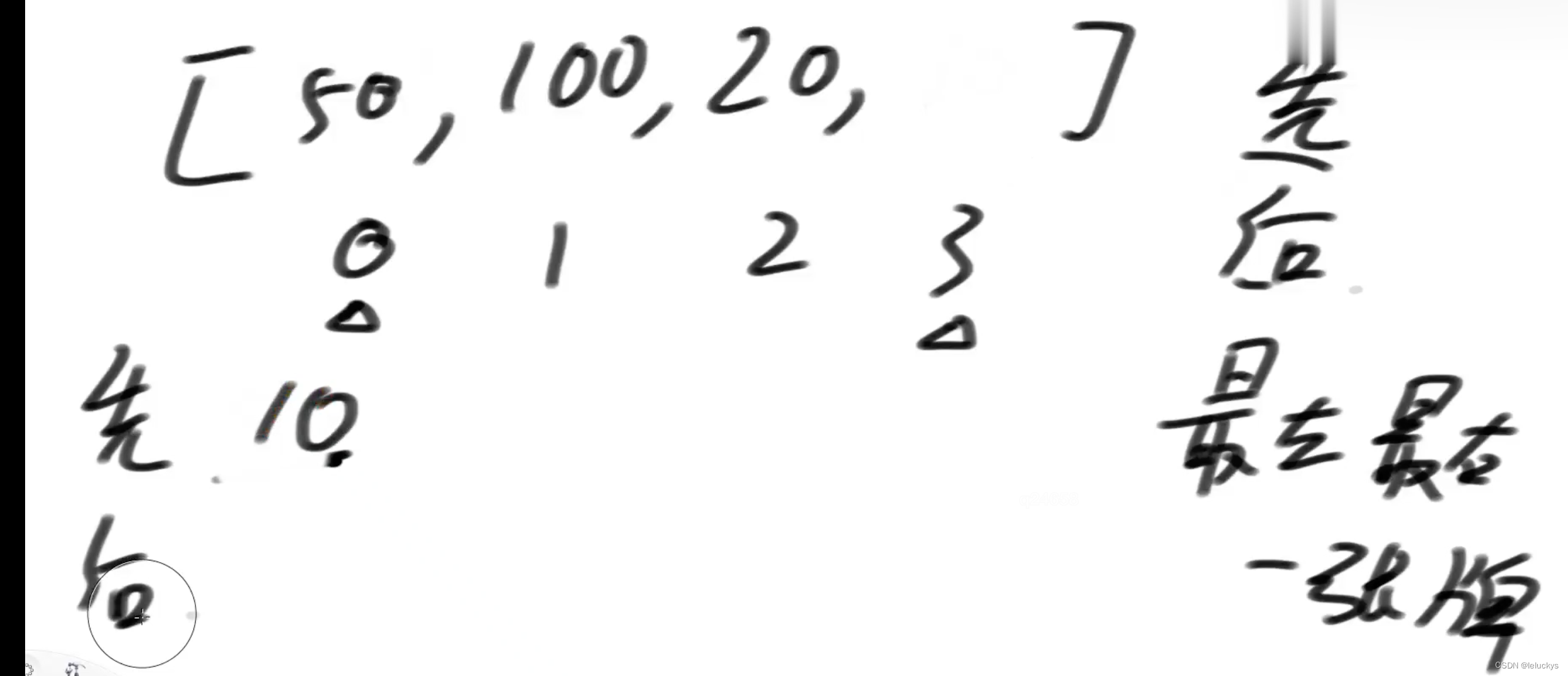
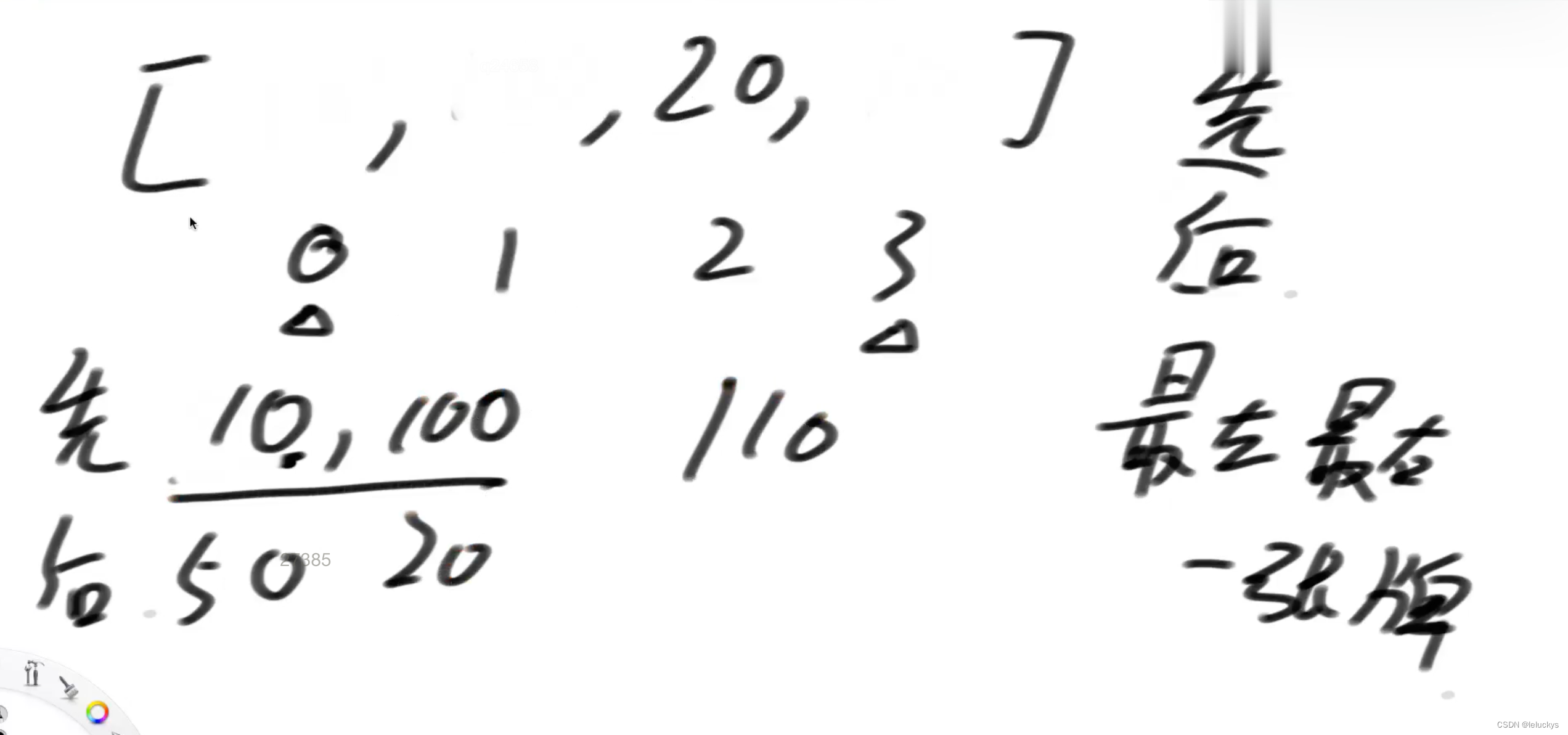
先手
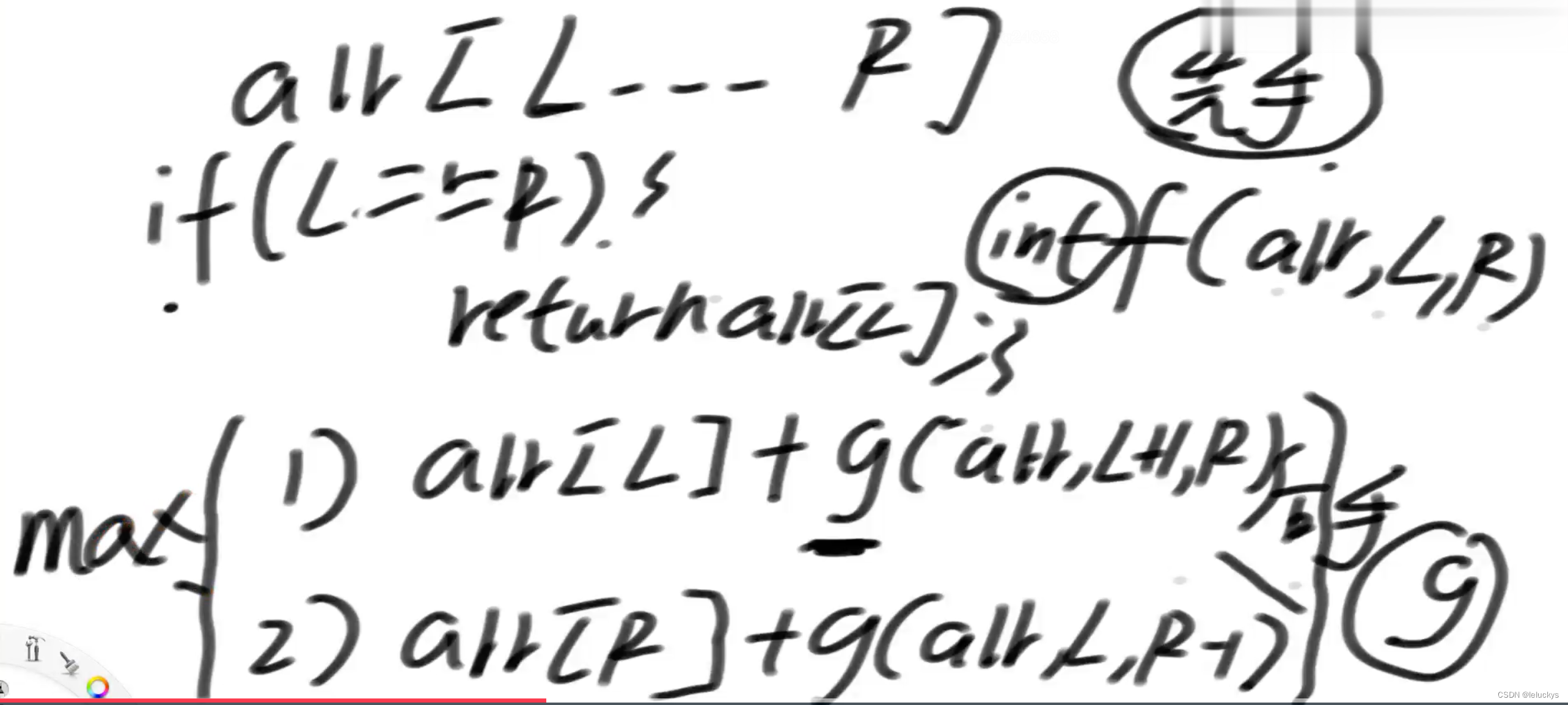
后手,后手能拿的只能是先手拿剩下的

优化1 傻缓存
优化二
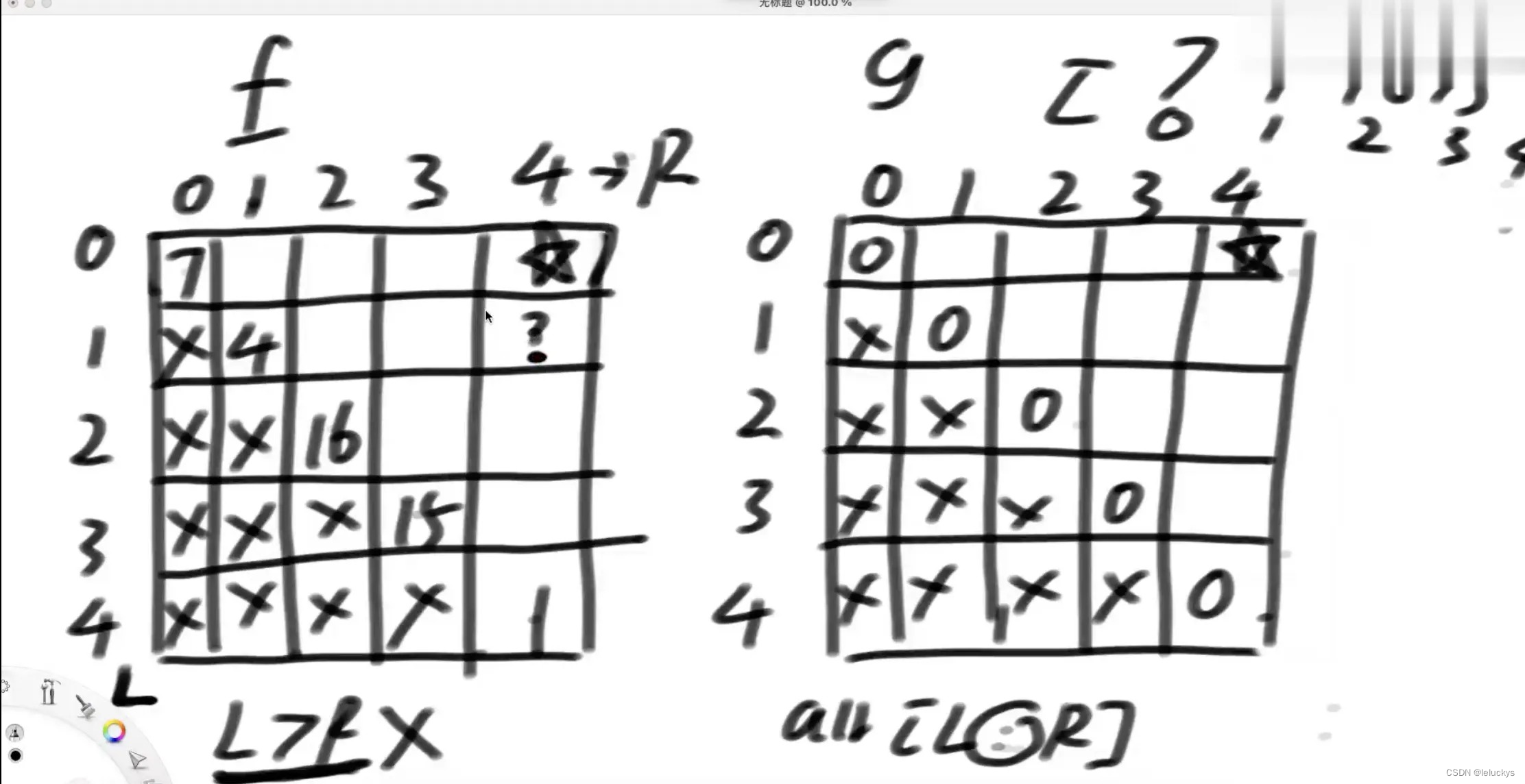
3.3代码
package class18;public class Code02_CardsInLine {// 根据规则,返回获胜者的分数public static int win1(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int first = f1(arr, 0, arr.length - 1);int second = g1(arr, 0, arr.length - 1);return Math.max(first, second);}// arr[L..R],先手获得的最好分数返回public static int f1(int[] arr, int L, int R) {if (L == R) {return arr[L];}int p1 = arr[L] + g1(arr, L + 1, R);int p2 = arr[R] + g1(arr, L, R - 1);return Math.max(p1, p2);}// // arr[L..R],这里面是对手做决定,后手获得的最好分数返回public static int g1(int[] arr, int L, int R) {if (L == R) {return 0;}int p1 = f1(arr, L + 1, R); // 对手拿走了L位置的数int p2 = f1(arr, L, R - 1); // 对手拿走了R位置的数return Math.min(p1, p2);}public static int win2(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int N = arr.length;int[][] fmap = new int[N][N];int[][] gmap = new int[N][N];for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {fmap[i][j] = -1;gmap[i][j] = -1;}}int first = f2(arr, 0, arr.length - 1, fmap, gmap);int second = g2(arr, 0, arr.length - 1, fmap, gmap);return Math.max(first, second);}// arr[L..R],先手获得的最好分数返回public static int f2(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {if (fmap[L][R] != -1) {return fmap[L][R];}int ans = 0;if (L == R) {ans = arr[L];} else {int p1 = arr[L] + g2(arr, L + 1, R, fmap, gmap);int p2 = arr[R] + g2(arr, L, R - 1, fmap, gmap);ans = Math.max(p1, p2);}fmap[L][R] = ans;return ans;}// // arr[L..R],后手获得的最好分数返回public static int g2(int[] arr, int L, int R, int[][] fmap, int[][] gmap) {if (gmap[L][R] != -1) {return gmap[L][R];}int ans = 0;if (L != R) {int p1 = f2(arr, L + 1, R, fmap, gmap); // 对手拿走了L位置的数int p2 = f2(arr, L, R - 1, fmap, gmap); // 对手拿走了R位置的数ans = Math.min(p1, p2);}gmap[L][R] = ans;return ans;}
3.4 优化代码
public static int win3(int[] arr) {if (arr == null || arr.length == 0) {return 0;}int N = arr.length;int[][] fmap = new int[N][N];int[][] gmap = new int[N][N];for (int i = 0; i < N; i++) {fmap[i][i] = arr[i];}for (int startCol = 1; startCol < N; startCol++) {int L = 0;int R = startCol;while (R < N) {fmap[L][R] = Math.max(arr[L] + gmap[L + 1][R], arr[R] + gmap[L][R - 1]);gmap[L][R] = Math.min(fmap[L + 1][R], fmap[L][R - 1]);L++;R++;}}return Math.max(fmap[0][N - 1], gmap[0][N - 1]);}public static void main(String[] args) {int[] arr = { 5, 7, 4, 5, 8, 1, 6, 0, 3, 4, 6, 1, 7 };System.out.println(win1(arr));System.out.println(win2(arr));System.out.println(win3(arr));}}相关文章:

第十九节:暴力递归到动态规划
一 动画规划的概念 优化出现重复解的递归 一旦写出递归来,改动态规划就很快 尝试策略和状态转移方程是一码事 学会尝试是攻克动态规划最本质的能力 如果你发现你有重复调用的过程,动态规划在算过一次之后把答案记下来,下回在越到重复调用过程…...

服务器部署spring项目jar包使用bat文件,省略每次输入java -jar了
echo off set pathC:\Program Files\Java\jre1.8.0_191\bin START "YiXiangZhengHe-8516" "%path%/java" -Xdebug -jar -Dspring.profiles.activeprod -Dserver.port8516 YiXiangZhengHe-0.0.1-SNAPSHOT.jar 将set path后面改成jre的bin文件夹 START 后…...

2024备忘知识点
1. adb shell dumpsys package f |grep fin 过滤查找指纹服务 1. adsp write /sys/kernel/boot_adsp/boot 1 Please change replace dev_dbg into dev_err in kernel file adsp-loader.c. Then check whether "write /sys/kernel/boot_adsp/…...

JS基础与高级应用: 性能优化
在现代Web开发中,性能优化已成为前端工程师必须掌握的核心技能之一。本文从URL输入到页面加载完成的全过程出发,深入分析了HTTP协议的演进、域名解析、代码层面性能优化以及编译与渲染的最佳实践。通过节流、防抖、重复请求合并等具体技术手段࿰…...
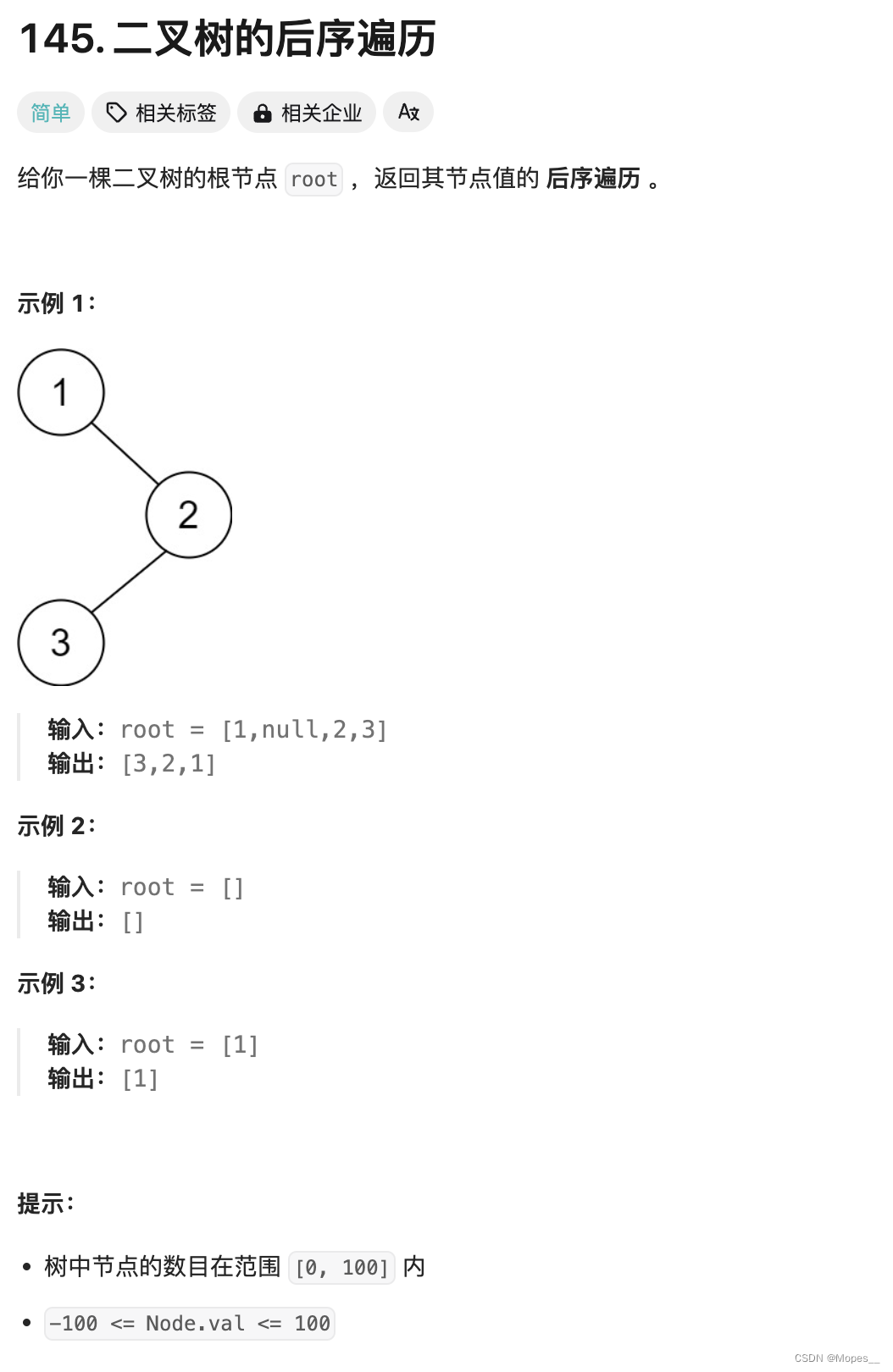
Python | Leetcode Python题解之第145题二叉树的后序遍历
题目: 题解: class Solution:def postorderTraversal(self, root: TreeNode) -> List[int]:def addPath(node: TreeNode):count 0while node:count 1res.append(node.val)node node.righti, j len(res) - count, len(res) - 1while i < j:res…...

公司面试题总结(二)
7. 说说 JavaScript 中的数据类型?存储上的差别? • 基本类型: o Number o String o Boolean o Undefined o null o symbol • 引用类型 o Object o Array o Function • 声明变量时不同的内存地址分配: o 简单类型的…...

人脸识别和 ArcFace:用于深度人脸识别的附加角边际损失
在本文中,您将发现一种 ArcFace 方法,该方法可获得用于人脸识别的高分辨特征。阅读本文后,你将了解: 人脸识别任务如何工作。如何计算人脸匹配。SoftMax 和 ArcFace 的直观区别。ArcFace 的几何解释。ArcFace 背后的数学原理本文假定您已经熟悉用于多类分类、检测和 SoftMax…...

双标引领:汽车软件安全的ASPICE与ISO21434之道
随着汽车行业的飞速发展,尤其是智能化、网联化趋势的加剧,汽车软件开发的复杂性和安全性需求日益提升。在这样的背景下,ASPICE标准和ISO21434安全标准应运而生,为汽车软件的开发和管理提供了坚实的支撑。 ASPICE(Auto…...

再度牵手,制造升级 | 毅达科技IMS OS+通用产品集+行业套件项目正式启动!
在数字化与智能制造的浪潮中,制造业企业纷纷加快转型步伐,力求通过技术创新实现生产效率与质量的双重提升。近日,广东毅达医疗科技股份有限公司(以下简称“毅达科技”)再次携手盘古信息,正式启动了IMS 数字…...

大疆智图_空三二维重建成果传输
一、软件环境 1.1 所需软件 1、 大疆智图:点击下载; 2、 ArcGIS Pro 3.1.5:点击下载,建议使用IDM或Aria2等多线程下载器; 3、 IDM下载器:点击下载,或自行搜索; 4、 Fas…...

python实现无人机航拍图片像素坐标转世界坐标
背景 已知相机参数(传感器宽度和高度、图像宽度和高度、焦距、相对航高、像主点坐标 ),在给定像素坐标的前提下,求世界坐标,大部分通过AI来实现,不知道哪个步骤有问题,望大家指正 脚本 impor…...

C#面:什么是 Windows 服务,它的生命周期与标准的 EXE 程序有什么不同
C#中的Windows服务是一种在后台运行的长时间运行的应用程序,它可以在Windows操作系统启动时自动启动,并在系统运行期间持续运行。与标准的EXE程序相比,Windows服务具有以下不同之处: 生命周期:Windows服务的生命周期与…...
Java基础面试题自测
文章目录 一、Java 中有哪 8 种基本数据类型?说说这 8 种基本数据类型对应的包装类型?二、包装类型的常量池技术了解么?三、为什么要有包装类型?四、什么是自动拆装箱?原理?四、遇到过自动拆箱引发的 NPE 问…...

【LeetCode 第 401 场周赛】K秒后第 N 个元素的值
文章目录 1. K秒后第 N 个元素的值🆗 1. K秒后第 N 个元素的值🆗 题目链接🔗 🐧解题思路: 前缀和 小规律🍎 🍎 从上图观察可知,规律一目了然,arr[i] arr[i] 对上一…...

游戏心理学Day10
习得性动机。 习得性动机也称社会性动机是指人与社会生活相联系的后天习得的动机,这类动机比原发性动机要多很多。 成就动机。 成就动机是指个人追求进步以及达到目标的内在动力。 在游戏中设计师总会担心过多的失败,会令玩家感到挫败进而离开游戏 对…...

MySQL表设计经验汇总篇
文章目录 1、命名规范2、选择合适的字段类型3、主键设计要合理4、选择合适的字段长度5、优先考虑逻辑删除,而不是物理删除6、每个表都需要添加通用字段7、一张表的字段不宜过多8、定义字段尽可能not null9、合理添加索引10、通过业务字段冗余来减少表关联11、避免使…...

Servlet基础(续集2)
HttpServletResponse web服务器接收到客户端的http的请求,针对这个请求,分别创建一个代表请求的HttpServletRequest对象,代表响应的一个HttpServletResponse 如果要获取客户端请求过来的参数:找HttpServletRequest如果要给客户端…...
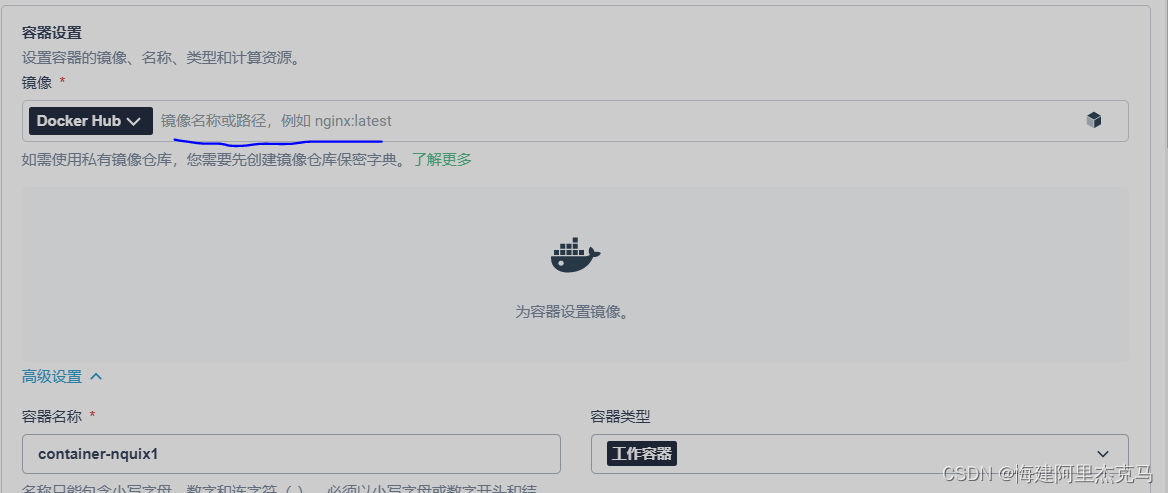
【云原生】创建harbor私有仓库及使用aliyun个人仓库
1.安装docker #删除已有dockersystemctl stop docker yum remove docker \docker-client \docker-client-latest \docker-common \docker-latest \docker-latest-logrotate \docker-logrotate \docker-engine #安装docker yum install -y docker-ce-20.10.1…...
什么是SOLIDWORKS科研版
随着科技的不断进步,工程设计和科学研究变得越来越复杂,需要更强大的工具来满足需求。SOLIDWORKS科研版就是在这样的背景下诞生的,它为科研人员和工程师提供了一套全方面、快捷的解决方案,以应对各种科研和工程挑战。 SOLIDWORKS科…...

微信小程序页面配置
页面配置 小程序的配置可以配置页面路径、窗口表现、tabBar等,分为全局配置和页面配置,全局配置针对所有页面生效,页面配置只针对当前页生效。 全局配置 (app.json) (1) 路径配置 pages 配置页面路径,未配置路径的页面无法被访…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

大模型多显卡多服务器并行计算方法与实践指南
一、分布式训练概述 大规模语言模型的训练通常需要分布式计算技术,以解决单机资源不足的问题。分布式训练主要分为两种模式: 数据并行:将数据分片到不同设备,每个设备拥有完整的模型副本 模型并行:将模型分割到不同设备,每个设备处理部分模型计算 现代大模型训练通常结合…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...
