0405习题总结-不定积分
文章目录
- 1 不定积分的基本概念
- 2 直接积分法-基本积分公式
- 3 第一换元法-凑微分形式法
- 4 第二类换元法
- 5 分部积分求不定积分
- 6 表格法积分
- 7 有理函数求积分
- 后记
1 不定积分的基本概念
例1
f(x)={x+1,x≥012e−x+12,x<0求∫f(x)dxf(x)= \begin{cases} x+1,\quad x\ge0\\ \frac{1}{2}e^{-x}+\frac{1}{2},\quad x\lt0\\ \end{cases}\\ 求\int{f(x)dx} f(x)={x+1,x≥021e−x+21,x<0求∫f(x)dx
解:f(x)在(−∞,+∞)上连续∫f(x)dx={12x2+x+C1,x≥0,C1为任意常数−12e−x+12x+C2,x<0,C2为任意常数F(x)作为f(x)的一个原函数,在x=0处连续那么C1=−12+C2,令C2=C(任意常数),则C1=−12+C∫f(x)dx={12x2+x−12+C,x≥0,C为任意常数−12e−x+12x+C,x<0解:f(x)在(-\infty,+\infty)上连续\\ \int{f(x)dx}= \begin{cases} \frac{1}{2}x^2+x+C_1,\quad x\ge0,C_1为任意常数\\ -\frac{1}{2}e^{-x}+\frac{1}{2}x+C_2,\quad x\lt0,C_2为任意常数\\ \end{cases}\\ F(x)作为f(x)的一个原函数,在x=0处连续\\ 那么C_1=-\frac{1}{2}+C_2,令C_2=C(任意常数),则C_1=-\frac{1}{2}+C\\ \int{f(x)dx}= \begin{cases} \frac{1}{2}x^2+x-\frac{1}{2}+C,\quad x\ge0,C为任意常数\\ -\frac{1}{2}e^{-x}+\frac{1}{2}x+C,\quad x\lt0\\ \end{cases}\\ 解:f(x)在(−∞,+∞)上连续∫f(x)dx={21x2+x+C1,x≥0,C1为任意常数−21e−x+21x+C2,x<0,C2为任意常数F(x)作为f(x)的一个原函数,在x=0处连续那么C1=−21+C2,令C2=C(任意常数),则C1=−21+C∫f(x)dx={21x2+x−21+C,x≥0,C为任意常数−21e−x+21x+C,x<0
注意:
- f(x)f(x)f(x)连续,F(x)可导。
- f(x)f(x)f(x)有第一类,第二类无穷间断点,则不存在原函数。
- f(x)f(x)f(x)有第二类震荡间断点时,可能存在原函数。
例2 ∫max{x3,x2,1}dx\int{max\{x^3,x^2,1\}dx}∫max{x3,x2,1}dx
解:令f(x)=max{x3,x2,1},则f(x)={x2,x≤−11,−1<x<1x3,x≥1f(x)在(−∞,+∞)上连续∫f(x)={13x3+C1,x≤−1x+C,−1<x<114x4+C2,x≥1F(x)在点x=−1出连续,所以−13+C1=−1+C,则C1=−23+CF(x)在点x=1出连续,所以14+C2=1+C,则C2=34+C∫f(x)={13x3−23+C,x≤−1x+C,−1<x<114x4+34+C,x≥1解:令f(x)=max\{x^3,x^2,1\},则\\ f(x)= \begin{cases} x^2,\quad x\le -1\\ 1,\quad -1\lt x\lt1\\ x^3,\quad x\ge1 \end{cases}\\ f(x)在(-\infty,+\infty)上连续\\ \int{f(x)}= \begin{cases} \frac{1}{3}x^3+C_1,\quad x\le -1\\ x+C,\quad -1\lt x\lt1\\ \frac{1}{4}x^4+C_2,\quad x\ge1 \end{cases}\\ F(x)在点x=-1出连续,所以-\frac{1}{3}+C_1=-1+C,则C_1=-\frac{2}{3}+C\\ F(x)在点x=1出连续,所以\frac{1}{4}+C_2=1+C,则C_2=\frac{3}{4}+C\\ \int{f(x)}= \begin{cases} \frac{1}{3}x^3-\frac{2}{3}+C,\quad x\le -1\\ x+C,\quad -1\lt x\lt1\\ \frac{1}{4}x^4+\frac{3}{4}+C,\quad x\ge1 \end{cases}\\ 解:令f(x)=max{x3,x2,1},则f(x)=⎩⎨⎧x2,x≤−11,−1<x<1x3,x≥1f(x)在(−∞,+∞)上连续∫f(x)=⎩⎨⎧31x3+C1,x≤−1x+C,−1<x<141x4+C2,x≥1F(x)在点x=−1出连续,所以−31+C1=−1+C,则C1=−32+CF(x)在点x=1出连续,所以41+C2=1+C,则C2=43+C∫f(x)=⎩⎨⎧31x3−32+C,x≤−1x+C,−1<x<141x4+43+C,x≥1
总结:分段函数求积分
- 确定在分段点连续
- 求分段积分
- 统一常数
例3 证明:函数arcsin(2x−1),arccos(1−2x),arctanx1−x都是1x−x2\arcsin(2x-1),\arccos(1-2x),\arctan\sqrt{\frac{x}{1-x}}都是\frac{1}{\sqrt{x-x^2}}arcsin(2x−1),arccos(1−2x),arctan1−xx都是x−x21的原函数
证明:通过原函数求导函数即可[arcsin(2x−1)]′=11−(2x−1)2⋅2=1x−x2[arccos(1−2x)]′=−11−(1−2x)2⋅−2=1x−x2[arctanx1−x]′=11+x1−x⋅(x1−x)′=1x−x2证明:通过原函数求导函数即可\\ [\arcsin(2x-1)]^{'}=\frac{1}{\sqrt{1-(2x-1)^2}}\cdot2=\frac{1}{\sqrt{x-x^2}}\\ [\arccos(1-2x)]^{'}=-\frac{1}{\sqrt{1-(1-2x)^2}}\cdot-2=\frac{1}{\sqrt{x-x^2}}\\ [\arctan\sqrt{\frac{x}{1-x}}]^{'}=\frac{1}{1+\frac{x}{1-x}}\cdot(\sqrt{\frac{x}{1-x}})^{'}=\frac{1}{\sqrt{x-x^2}} 证明:通过原函数求导函数即可[arcsin(2x−1)]′=1−(2x−1)21⋅2=x−x21[arccos(1−2x)]′=−1−(1−2x)21⋅−2=x−x21[arctan1−xx]′=1+1−xx1⋅(1−xx)′=x−x21
2 直接积分法-基本积分公式
例1 ∫x41+x2dx\int{\frac{x^4}{1+x^2}dx}∫1+x2x4dx
多项式除法
解:∫x41+x2dx=∫(x2−1+11+x2)dx=13x3−x+arctanx+C解:\int{\frac{x^4}{1+x^2}dx}=\int{(x^2-1+\frac{1}{1+x^2})dx}\\ =\frac{1}{3}x^3-x+\arctan x+C 解:∫1+x2x4dx=∫(x2−1+1+x21)dx=31x3−x+arctanx+C
例2 求∫1x8(1+x2)dx\int{\frac{1}{x^8(1+x^2)}dx}∫x8(1+x2)1dx
高次多项式与低次多项式+常数乘积
解:∫1x8(1+x2)dx=∫1−x8+x8x8(1+x2)dx=∫(1+x4)(1−x2)x8dx+∫11+x2dx=1x−13x3+15x5−17x7+arctanx+C解:\int{\frac{1}{x^8(1+x^2)}dx}=\int{\frac{1-x^8+x^8}{x^8(1+x^2)}dx}\\ =\int{\frac{(1+x^4)(1-x^2)}{x^8}dx}+\int{\frac{1}{1+x^2}dx}\\ =\frac{1}{x}-\frac{1}{3x^3}+\frac{1}{5x^5}-\frac{1}{7x^7}+\arctan x+C 解:∫x8(1+x2)1dx=∫x8(1+x2)1−x8+x8dx=∫x8(1+x4)(1−x2)dx+∫1+x21dx=x1−3x31+5x51−7x71+arctanx+C
例3 求∫tan2xdx\int{\tan^2xdx}∫tan2xdx
解:∫tan2xdx=∫(sec2x−1)dx=tanx−x+C解:\int{\tan^2xdx}=\int{(\sec^2x-1)dx}=\tan x-x+C 解:∫tan2xdx=∫(sec2x−1)dx=tanx−x+C
例4 求∫11+cos2xdx\int{\frac{1}{1+\cos2x}dx}∫1+cos2x1dx
解:∫11+cos2xdx=∫12cos2xdx=12tanx+C解:\int{\frac{1}{1+\cos2x}dx}=\int{\frac{1}{2\cos^2x}dx}\\ =\frac{1}{2}\tan x+C 解:∫1+cos2x1dx=∫2cos2x1dx=21tanx+C
例5 求∫1sin2xcos2xdx\int{\frac{1}{\sin^2x\cos^2x}dx}∫sin2xcos2x1dx
解:∫1sin2xcos2xdx=∫sin2x+cos2xsin2xcos2xdx=∫sec2xdx+∫csc2xdx=tanx−cotx+C解:\int{\frac{1}{\sin^2x\cos^2x}dx}=\int{\frac{\sin^2x+\cos^2x}{\sin^2x\cos^2x}dx}\\ =\int{\sec^2xdx}+\int{\csc^2xdx}=\tan x-\cot x+C 解:∫sin2xcos2x1dx=∫sin2xcos2xsin2x+cos2xdx=∫sec2xdx+∫csc2xdx=tanx−cotx+C
3 第一换元法-凑微分形式法
∫{f[g(x)]g′(x)dx}=[∫f(t)dt]t=g(x)\int{\{f[g(x)]g^{'}(x)dx\}}=[\int{f(t)dt}]_{t=g(x)}∫{f[g(x)]g′(x)dx}=[∫f(t)dt]t=g(x)
常见凑微分公式:
-
∫f(ax+b)dx=1a∫f(ax+b)d(ax+b)\int{f(ax+b)dx}=\frac{1}{a}\int{f(ax+b)d(ax+b)}∫f(ax+b)dx=a1∫f(ax+b)d(ax+b)
-
∫f(ex)exdx=∫f(ex)dex\int{f(e^x)e^xdx}=\int{f(e^x)de^x}∫f(ex)exdx=∫f(ex)dex ∫f(ax)axdx=1lna∫f(ax)dax\quad \int{f(a^x)a^xdx}=\frac{1}{\ln a}\int{f(a^x)da^x}∫f(ax)axdx=lna1∫f(ax)dax
-
∫f(xμ)xμ−1dx=1μ∫f(xμ)d(xμ)\int{f(x^\mu)x^{\mu-1}dx}=\frac{1}{\mu}\int{f(x^\mu)d(x^\mu)}∫f(xμ)xμ−1dx=μ1∫f(xμ)d(xμ)
-
∫f(1x)1x2dx=−∫f(1x)d(1x)\int{f(\frac{1}{x})\frac{1}{x^2}dx}=-\int{f(\frac{1}{x})d(\frac{1}{x}})∫f(x1)x21dx=−∫f(x1)d(x1)
-
∫f(x)1xdx=2∫f(x)d(x)\int{f(\sqrt{x})\frac{1}{\sqrt{x}}dx}=2\int{f(\sqrt{x})d(\sqrt{x})}∫f(x)x1dx=2∫f(x)d(x)
-
∫f(lnx)1xdx=∫f(lnx)d(lnx)∫f(xlnx)(1+lnx)dx=∫f(xlnx)d(xlnx)\int{f(\ln x)\frac{1}{x}dx}=\int{f(\ln x)d(\ln x)}\quad \int{f(x\ln x)(1+\ln x)dx}=\int{f(x\ln x)d(x\ln x)}∫f(lnx)x1dx=∫f(lnx)d(lnx)∫f(xlnx)(1+lnx)dx=∫f(xlnx)d(xlnx)
-
三角函数凑微分
- ∫f(sinx)cosxdx=∫f(sinx)d(sinx)\int{f(\sin x)\cos xdx}=\int{f(\sin x)d(\sin x)}∫f(sinx)cosxdx=∫f(sinx)d(sinx)
- ∫f(cosx)sinxdx=−∫f(cosx)d(cosx)\int{f(\cos x)\sin xdx}=-\int{f(\cos x)d(\cos x)}∫f(cosx)sinxdx=−∫f(cosx)d(cosx)
- ∫f(tanx)sec2xdx=∫f(tanx)d(tanx)\int{f(\tan x)\sec^2xdx}=\int{f(\tan x)d(\tan x)}∫f(tanx)sec2xdx=∫f(tanx)d(tanx)
- ∫f(cotx)csc2xdx=−∫f(cotx)d(cotx)\int{f(\cot x)\csc^2xdx}=-\int{f(\cot x)d(\cot x)}∫f(cotx)csc2xdx=−∫f(cotx)d(cotx)
- ∫f(secx)secxtanxdx=∫f(secx)d(secx)\int{f(\sec x)\sec x\tan xdx}=\int{f(\sec x)d(\sec x)}∫f(secx)secxtanxdx=∫f(secx)d(secx)
- ∫f(cscx)cscxcotxdx=−∫f(cscx)d(cscx)\int{f(\csc x)\csc x\cot xdx}=-\int{f(\csc x)d(\csc x)}∫f(cscx)cscxcotxdx=−∫f(cscx)d(cscx)
-
反三角函数
- ∫f(arctanx)11+x2dx=∫f(arctanx)d(arctanx)\int{f(\arctan x)\frac{1}{1+x^2}dx}=\int{f(\arctan x)d(\arctan x)}∫f(arctanx)1+x21dx=∫f(arctanx)d(arctanx)
- ∫f(arccotx)11+x2dx=−∫f(arccotx)d(arccotx)\int{f(arccot x)\frac{1}{1+x^2}dx}=-\int{f(arccot x)d(arccot x)}∫f(arccotx)1+x21dx=−∫f(arccotx)d(arccotx)
- ∫f(arcsinx)11−x2dx=∫f(arcsinx)d(arcsinx)\int{f(\arcsin x)\frac{1}{\sqrt{1-x^2}}dx}=\int{f(\arcsin x)d(\arcsin x)}∫f(arcsinx)1−x21dx=∫f(arcsinx)d(arcsinx)
- ∫f(arccosx)11−x2dx=−∫f(arccosx)d(arccosx)\int{f(\arccos x)\frac{1}{\sqrt{1-x^2}}dx}=-\int{f(\arccos x)d(\arccos x)}∫f(arccosx)1−x21dx=−∫f(arccosx)d(arccosx)
-
∫f(x+1x)(1−1x2)dx=∫f(x+1x)d(x+1x)∫f(x−1x)(1+1x2)dx=∫f(x−1x)d(x−1x)\int{f(x+\frac{1}{x})(1-\frac{1}{x^2})dx}=\int{f(x+\frac{1}{x})d(x+\frac{1}{x})}\quad \int{f(x-\frac{1}{x})(1+\frac{1}{x^2})dx}=\int{f(x-\frac{1}{x})d(x-\frac{1}{x})}∫f(x+x1)(1−x21)dx=∫f(x+x1)d(x+x1)∫f(x−x1)(1+x21)dx=∫f(x−x1)d(x−x1)
例1 ∫tan5xsec3xdx\int{\tan^5xsec^3xdx}∫tan5xsec3xdx
解:∫tan5xsec3xdx=∫(sec2x−1)2sec2xd(secx)=∫(sec6x−2sec4x+sec2x)d(secx)=17sec7x−25sec5x+13sec3x+C解:\int{\tan^5xsec^3xdx}=\int{(sec^2x-1)^2sec^2xd(secx)}\\ =\int{(sec^6x-2sec^4x+sec^2x)d(secx)}=\frac{1}{7}sec^7x-\frac{2}{5}sec^5x+\frac{1}{3}sec^3x+C 解:∫tan5xsec3xdx=∫(sec2x−1)2sec2xd(secx)=∫(sec6x−2sec4x+sec2x)d(secx)=71sec7x−52sec5x+31sec3x+C
例2 ∫ln(1+x)−lnxx(1+x)dx\int{\frac{\ln(1+x)-\ln x}{x(1+x)}dx}∫x(1+x)ln(1+x)−lnxdx
解:∫ln(1+x)−lnxx(1+x)dx=−∫[ln(1+x)−lnx]d[ln(1+x)−lnx]=−12[ln(1+x)−lnx]2+C解:\int{\frac{\ln(1+x)-\ln x}{x(1+x)}dx}=-\int{[\ln(1+x)-\ln x]d[\ln(1+x)-\ln x]}\\ =-\frac{1}{2}[\ln(1+x)-\ln x]^2+C 解:∫x(1+x)ln(1+x)−lnxdx=−∫[ln(1+x)−lnx]d[ln(1+x)−lnx]=−21[ln(1+x)−lnx]2+C
例3 ∫(1+2x2)ex22−3xex2dx\int{\frac{(1+2x^2)e^{x^2}}{2-3xe^{x^2}}dx}∫2−3xex2(1+2x2)ex2dx
解:∫(1+2x2)ex22−3xex2dx=−13∫12−3xex2d(2−3xex2)=−13ln∣2−3xex2∣+C解:\int{\frac{(1+2x^2)e^{x^2}}{2-3xe^{x^2}}dx}=-\frac{1}{3}\int{\frac{1}{2-3xe^{x^2}}d(2-3xe^{x^2})}=-\frac{1}{3}\ln|2-3xe^{x^2}|+C 解:∫2−3xex2(1+2x2)ex2dx=−31∫2−3xex21d(2−3xex2)=−31ln∣2−3xex2∣+C
例4 ∫earctan1+x(2+x)1+xdx\int{\frac{e^{\arctan\sqrt{1+x}}}{(2+x)\sqrt{1+x}}dx}∫(2+x)1+xearctan1+xdx
解:∫earctan1+x(2+x)1+xdx=2∫earctan1+xd(arctan1+x)=2earctan1+x+C解:\int{\frac{e^{\arctan\sqrt{1+x}}}{(2+x)\sqrt{1+x}}dx}=2\int{e^{\arctan\sqrt{1+x}}d(\arctan\sqrt{1+x})}\\ =2e^{\arctan\sqrt{1+x}}+C 解:∫(2+x)1+xearctan1+xdx=2∫earctan1+xd(arctan1+x)=2earctan1+x+C
例5 ∫lntanx2sinxdx\int{\frac{\ln\tan\frac{x}{2}}{\sin x}dx}∫sinxlntan2xdx
解:∫lntanx2sinxdx=∫lntanx2d(lntanx2)=12ln2tanx2+C解:\int{\frac{\ln\tan\frac{x}{2}}{\sin x}dx}=\int{\ln\tan\frac{x}{2}d(\ln\tan\frac{x}{2})}\\ =\frac{1}{2}\ln^2\tan\frac{x}{2}+C 解:∫sinxlntan2xdx=∫lntan2xd(lntan2x)=21ln2tan2x+C
4 第二类换元法
∫f(x)dx=[∫[f(ϕ(t))]ϕ′(t)dt]t=ϕ−1(x)\int{f(x)dx}=[\int{[f(\phi(t))]\phi^{'}(t)dt}]_{t=\phi^{-1}(x)}∫f(x)dx=[∫[f(ϕ(t))]ϕ′(t)dt]t=ϕ−1(x)
- 三大换元
- 三角换元
- 被积函数含有a2−x2\sqrt{a^2-x^2}a2−x2:令x=asintx=a\sin tx=asint
- 被积函数含有x2+a2\sqrt{x^2+a^2}x2+a2:令x=atantx=a\tan tx=atant
- 被积函数含有x2−a2\sqrt{x^2-a^2}x2−a2:令x=asectx=a\sec tx=asect
- 当被积函数含有(x2+a2)n(x^2+a^2)^n(x2+a2)n也考虑x=atantx=a\tan tx=atant
- 当被积函数含有(x2−a2)n(x^2-a^2)^n(x2−a2)n也考虑x=asectx=a\sec tx=asect
- 根式代换
- 被积函数含有ax+bcx+dn:令ax+bcx+dn=t\sqrt[n]{\frac{ax+b}{cx+d}}:令\sqrt[n]{\frac{ax+b}{cx+d}}=tncx+dax+b:令ncx+dax+b=t
- 被积函数含有ax+bn:令ax+bn=t\sqrt[n]{ax+b}:令\sqrt[n]{ax+b}=tnax+b:令nax+b=t
- 被积函数含有ax+bn,ax+bm:令ax+bk=t,k为m,n的最小公倍数\sqrt[n]{ax+b},\sqrt[m]{ax+b}:令\sqrt[k]{ax+b}=t,k为m,n的最小公倍数nax+b,max+b:令kax+b=t,k为m,n的最小公倍数
- 倒代换
- 当分母方次高于分子方次,可以考虑倒代换。
- 三角换元
例1 求∫1(1+x2)2dx\int{\frac{1}{(1+x^2)^2}dx}∫(1+x2)21dx
解:解法一.∫1(1+x2)2dx=∫1+x2−x2(1+x2)2dx=arctanx+12∫xd(11+x2)==arctanx+12x1+x2−12∫(11+x2)dx=12arctanx+x2(1+x2)+C解法二.令x=tanx∫1(1+x2)2dx=∫1(1+tan2x)2dtanx=∫cos2tdt=14sintcost−12t+C=12arctanx+x2(1+x2)+C解:解法一.\int{\frac{1}{(1+x^2)^2}dx}=\int{\frac{1+x^2-x^2}{(1+x^2)^2}dx}\\ =\arctan x+\frac{1}{2}\int{xd(\frac{1}{1+x^2})}=\\ =\arctan x+\frac{1}{2}\frac{x}{1+x^2}-\frac{1}{2}\int{(\frac{1}{1+x^2})dx}\\ =\frac{1}{2}\arctan x+\frac{x}{2(1+x^2)}+C\\ 解法二.令x=\tan x\\ \int{\frac{1}{(1+x^2)^2}dx}=\int{\frac{1}{(1+\tan^2x)^2}d\tan x}\\ =\int{\cos^2tdt}=\frac{1}{4}\sin t\cos t-\frac{1}{2}t+C =\frac{1}{2}\arctan x+\frac{x}{2(1+x^2)}+C 解:解法一.∫(1+x2)21dx=∫(1+x2)21+x2−x2dx=arctanx+21∫xd(1+x21)==arctanx+211+x2x−21∫(1+x21)dx=21arctanx+2(1+x2)x+C解法二.令x=tanx∫(1+x2)21dx=∫(1+tan2x)21dtanx=∫cos2tdt=41sintcost−21t+C=21arctanx+2(1+x2)x+C
例2 求∫1(ax2+b)ndx,n>1,a>0\int{\frac{1}{(ax^2+b)^n}dx},n>1,a>0∫(ax2+b)n1dx,n>1,a>0
解:∫1(ax2+b)ndx=1b∫1(ax2+b)n−1dx+12b(n−1)∫xd1(ax2+b)n−1=2bn−2b−22b(n−1)∫1(ax2+b)n−1dx+x2b(n−1)(x2+1)n−1解:\int{\frac{1}{(ax^2+b)^n}dx}=\frac{1}{b}\int{\frac{1}{(ax^2+b)^{n-1}}dx}+\frac{1}{2b(n-1)}\int{xd{\frac{1}{(ax^2+b)^{n-1}}}}\\ =\frac{2bn-2b-2}{2b(n-1)}\int{\frac{1}{(ax^2+b)^{n-1}}dx}+\frac{x}{2b(n-1)(x^2+1)^{n-1}} 解:∫(ax2+b)n1dx=b1∫(ax2+b)n−11dx+2b(n−1)1∫xd(ax2+b)n−11=2b(n−1)2bn−2b−2∫(ax2+b)n−11dx+2b(n−1)(x2+1)n−1x
例3 求∫1x+x3dx\int{\frac{1}{\sqrt{x}+\sqrt[3]{x}}dx}∫x+3x1dx
解:令x6=t,则x=t6,dx=6t5∫1x+x3dx=∫6t5t3+t2dt=∫6(t2−t+1−1t+1)dt=2t3−3t2+6t−6ln∣t+1∣+C=2x12−3x13+6x16−6ln∣x16+1∣+C解:令\sqrt[6]{x}=t,则x=t^6,dx=6t^5\\ \int{\frac{1}{\sqrt{x}+\sqrt[3]{x}}dx}=\int{\frac{6t^5}{t^3+t^2}dt}\\ =\int{6(t^2-t+1-\frac{1}{t+1})dt}=2t^3-3t^2+6t-6\ln|t+1|+C\\ =2x^{\frac{1}{2}}-3x^{\frac{1}{3}}+6x^{\frac{1}{6}}-6\ln|x^{\frac{1}{6}}+1|+C 解:令6x=t,则x=t6,dx=6t5∫x+3x1dx=∫t3+t26t5dt=∫6(t2−t+1−t+11)dt=2t3−3t2+6t−6ln∣t+1∣+C=2x21−3x31+6x61−6ln∣x61+1∣+C
例4 求∫11+x+x+1dx\int{\frac{1}{1+\sqrt{x}+\sqrt{x+1}}dx}∫1+x+x+11dx
解:令t=x+x+1,x=14(t−1t)2dt=12(t−1t)(1+1t2)dt∫11+x+x+1dx=12∫t−1t3dt=−12t+14t2+C=14(x+1−x)(x+1−x−2)+C解:令t=\sqrt{x}+\sqrt{x+1},x=\frac{1}{4}(t-\frac{1}{t})^2\\ dt=\frac{1}{2}(t-\frac{1}{t})(1+\frac{1}{t^2})dt\\ \int{\frac{1}{1+\sqrt{x}+\sqrt{x+1}}dx}=\frac{1}{2}\int{\frac{t-1}{t^3}dt}\\ =-\frac{1}{2t}+\frac{1}{4t^2}+C=\frac{1}{4}(\sqrt{x+1}-\sqrt{x})(\sqrt{x+1}-\sqrt{x}-2)+C 解:令t=x+x+1,x=41(t−t1)2dt=21(t−t1)(1+t21)dt∫1+x+x+11dx=21∫t3t−1dt=−2t1+4t21+C=41(x+1−x)(x+1−x−2)+C
例5求∫1(1+x)1−x2dx\int{\frac{1}{(1+x)\sqrt{1-x^2}}dx}∫(1+x)1−x21dx
解:令x=sint,dx=cost∫1(1+x)1−x2dx=∫11+sintdt=∫(sec2t−tantsect)dt=tant−sect+C=x−11−x2+C解:令x=\sin t,dx=\cos t\\ \int{\frac{1}{(1+x)\sqrt{1-x^2}}dx}=\int{\frac{1}{1+\sin t}dt}\\ =\int{(\sec^2t-\tan t\sec t)dt}=\tan t-\sec t+C\\ =\frac{x-1}{\sqrt{1-x^2}}+C 解:令x=sint,dx=cost∫(1+x)1−x21dx=∫1+sint1dt=∫(sec2t−tantsect)dt=tant−sect+C=1−x2x−1+C
例6 ∫1x(x6+4)dx\int{\frac{1}{x(x^6+4)}dx}∫x(x6+4)1dx
解:∫1x(x6+4)dx=14∫4+x6−x6x(x6+4)dx=124lnx6x6+4+C解:\int{\frac{1}{x(x^6+4)}dx}=\frac{1}{4}\int{\frac{4+x^6-x^6}{x(x^6+4)}dx}\\ =\frac{1}{24}\ln\frac{x^6}{x^6+4}+C 解:∫x(x6+4)1dx=41∫x(x6+4)4+x6−x6dx=241lnx6+4x6+C
∫1x(axn+b)dx=1bnln∣xnaxn+b∣,bn≠0\int{\frac{1}{x(ax^n+b)}dx}=\frac{1}{bn}\ln|\frac{x^n}{ax^n+b}|,bn\not=0∫x(axn+b)1dx=bn1ln∣axn+bxn∣,bn=0
例7 求∫11+ex2+ex3+ex6dx\int{\frac{1}{1+e^{\frac{x}{2}}+e^{\frac{x}{3}}+e^{\frac{x}{6}}}dx}∫1+e2x+e3x+e6x1dx
解:令ex6=t,x=6lnt,dx=6tdt原式=∫11+t3+t2+t⋅6tdt=∫6(t2+1)(t+1)tdt6(t2+1)(t+1)t=at+bt+1+cx+dt2+1计算的a=6,b=−3,c=−3,d=−3上式=∫(6t−3t+1−3t+1t2+1)dt=6ln∣t∣−3ln∣t+1∣−32ln∣t2+1∣−3arctant+C=x−3ln∣ex6+1∣−32ln∣ex3+1∣−3arctanex6+C解:令e^{\frac{x}{6}}=t,x=6\ln t,dx=\frac{6}{t}dt\\ 原式=\int{\frac{1}{1+t^3+t^2+t}\cdot\frac{6}{t}dt}\\ =\int{\frac{6}{(t^2+1)(t+1)t}dt}\\ \frac{6}{(t^2+1)(t+1)t}=\frac{a}{t}+\frac{b}{t+1}+\frac{cx+d}{t^2+1}\\ 计算的a=6,b=-3,c=-3,d=-3\\ 上式=\int{(\frac{6}{t}-\frac{3}{t+1}-3\frac{t+1}{t^2+1})dt}\\ =6\ln|t|-3\ln|t+1|-\frac{3}{2}\ln|t^2+1|-3\arctan t+C\\ =x-3\ln|e^{\frac{x}{6}}+1|-\frac{3}{2}\ln|e^{\frac{x}{3}}+1|-3\arctan e^{\frac{x}{6}}+C 解:令e6x=t,x=6lnt,dx=t6dt原式=∫1+t3+t2+t1⋅t6dt=∫(t2+1)(t+1)t6dt(t2+1)(t+1)t6=ta+t+1b+t2+1cx+d计算的a=6,b=−3,c=−3,d=−3上式=∫(t6−t+13−3t2+1t+1)dt=6ln∣t∣−3ln∣t+1∣−23ln∣t2+1∣−3arctant+C=x−3ln∣e6x+1∣−23ln∣e3x+1∣−3arctane6x+C
5 分部积分求不定积分
∫udv=vu−∫vdu\int{udv}=vu-\int{vdu}∫udv=vu−∫vdu
分部积分原则:
- ∫vdu比∫udv\int{vdu}比\int{udv}∫vdu比∫udv好求
- 分部积分选u的优先级别:反,对,幂,指,三
- 循环积分:关于于不定积分的方程
例1 求∫xsin2xdx\int{x\sin^2xdx}∫xsin2xdx
分析:sin2x\sin^2xsin2x优先降幂
解:∫xsin2xdx=∫x⋅1−cos2x2dx=14x2−∫12xcos2xdx=14x2−14∫xdsin2x=14x2−14xsin2x−18cos2x+C解:\int{x\sin^2xdx}=\int{x\cdot\frac{1-\cos2x}{2}dx}\\ =\frac{1}{4}x^2-\int{\frac{1}{2}x\cos2xdx}=\frac{1}{4}x^2-\frac{1}{4}\int{xd\sin2x}\\ =\frac{1}{4}x^2-\frac{1}{4}x\sin2x-\frac{1}{8}\cos2x+C 解:∫xsin2xdx=∫x⋅21−cos2xdx=41x2−∫21xcos2xdx=41x2−41∫xdsin2x=41x2−41xsin2x−81cos2x+C
例2 求∫x2e2xex\int{x^2e^{2x}}ex∫x2e2xex
解:∫x2e2xdx=12∫x2de2x=12x2e2x−12∫e2xdx2=12x2e2x−12∫xde2x=12x2e2x−12xe2x+14e2x+C解:\int{x^2e^{2x}}dx=\frac{1}{2}\int{x^2de^{2x}}\\ =\frac{1}{2}x^2e^{2x}-\frac{1}{2}\int{e^{2x}dx^2}=\frac{1}{2}x^2e^{2x}-\frac{1}{2}\int{xde^{2x}}\\ =\frac{1}{2}x^2e^{2x}-\frac{1}{2}xe^{2x}+\frac{1}{4}e^{2x}+C 解:∫x2e2xdx=21∫x2de2x=21x2e2x−21∫e2xdx2=21x2e2x−21∫xde2x=21x2e2x−21xe2x+41e2x+C
∫xmenxdx=1nxmenx−mn∫xm−1enxdx\int{x^me^{nx}dx}=\frac{1}{n}x^me^{nx}-\frac{m}{n}\int{x^{m-1}e^{nx}dx}∫xmenxdx=n1xmenx−nm∫xm−1enxdx
例3 求∫arctanexe2xdx{\int\frac{\arctan e^x}{e^{2x}}dx}∫e2xarctanexdx
解:∫arctanexe2xdx=−12∫arctanexde−2x=−12e−2xarctanex+12∫ex(1e2x−11+e2x)dx=−arctanex2e2x−12ex−12arctanex+C解:\int{\frac{\arctan e^x}{e^{2x}}dx}=-\frac{1}{2}\int{\arctan e^xde^{-2x}}\\ =-\frac{1}{2}e^{-2x}\arctan e^x+\frac{1}{2}\int{e^x(\frac{1}{e^{2x}}-\frac{1}{1+e^{2x}})dx}\\ =-\frac{\arctan e^x}{2e^{2x}}-\frac{1}{2e^x}-\frac{1}{2}\arctan e^x+C 解:∫e2xarctanexdx=−21∫arctanexde−2x=−21e−2xarctanex+21∫ex(e2x1−1+e2x1)dx=−2e2xarctanex−2ex1−21arctanex+C
例4 求∫sec3xdx\int{sec^3xdx}∫sec3xdx
解:∫sec3xdx=∫secxdtanx=secxtanx−∫tanxdsecx=secxtanx−∫(sec3x−secx)dx∫sec3x=12secxtanx+12ln∣secx+tanx∣+C解:\int{sec^3xdx=\int{secxd\tan x}}=\sec x\tan x-\int{\tan xd\sec x}\\ =\sec x\tan x-\int{(\sec^3x-\sec x)dx}\\ \int{sec^3x}=\frac{1}{2}\sec x\tan x+\frac{1}{2}\ln|\sec x+\tan x|+C 解:∫sec3xdx=∫secxdtanx=secxtanx−∫tanxdsecx=secxtanx−∫(sec3x−secx)dx∫sec3x=21secxtanx+21ln∣secx+tanx∣+C
例5 f(x)f(x)f(x)的一个原函数为xcosxx\cos xxcosx,求∫x⋅f′(x)dx\int{x\cdot f^{'}(x)dx}∫x⋅f′(x)dx
解:由已知得,∫f(x)dx=xcosx+Cf(x)=(xcosx)′=cosx−xsinx∫x⋅f′(x)dx=∫xdf(x)=xf(x)−∫f(x)dx=x(cosx−xsinx)−xcosx+C=−x2sinx+C解:由已知得,\int{f(x)dx}=x\cos x+C\\ f(x)=(x\cos x)^{'}=\cos x-x\sin x\\ \int{x\cdot f^{'}(x)dx}=\int{xdf(x)}=xf(x)-\int{f(x)dx}\\ =x(\cos x-x\sin x)-x\cos x+C=-x^2\sin x+C 解:由已知得,∫f(x)dx=xcosx+Cf(x)=(xcosx)′=cosx−xsinx∫x⋅f′(x)dx=∫xdf(x)=xf(x)−∫f(x)dx=x(cosx−xsinx)−xcosx+C=−x2sinx+C
例6 设F(x)是f(x)F(x)是f(x)F(x)是f(x) 的原函数, 且当x≥0时x\ge0时x≥0时,f(x)⋅F(x)=xex2(1+x)2f(x)\cdot F(x)=\frac{xe^x}{2(1+x)^2}f(x)⋅F(x)=2(1+x)2xex,已知F(0)=1,F(x)>0F(0)=1,F(x)\gt0F(0)=1,F(x)>0.求f(x)f(x)f(x)
解:有已知得F′(x)=f(x)f(x)⋅F(x)=xex2(1+x)2两边求积分∫f(x)⋅F(x)dx=∫xex2(1+x)2dxF2(x)=−∫xexd(11+x)=ex1+x+C因为F(0)=1,所以C=0因为x≥0时,F(x)>0,所以F(x)=ex1+xf(x)=F′(x)=(ex1+x)′=121ex1+x⋅xex(1+x2)=xe122(1+x)32解:有已知得 F^{'}(x)=f(x)\\ f(x)\cdot F(x)=\frac{xe^x}{2(1+x)^2}两边求积分\\ \int{f(x)\cdot F(x)dx}=\int{\frac{xe^x}{2(1+x)^2}}dx\\ F^2(x)=-\int{xe^xd(\frac{1}{1+x})}=\frac{e^x}{1+x}+C\\ 因为F(0)=1,所以C=0\\ 因为x\ge0时,F(x)\gt0,所以F(x)=\sqrt{\frac{e^x}{1+x}}\\ f(x)=F^{'}(x)=(\sqrt{\frac{e^x}{1+x}})^{'}=\frac{1}{2}\frac{1}{\sqrt{\frac{e^x}{1+x}}}\cdot\frac{xe^x}{(1+x^2)}\\ =\frac{xe^{\frac{1}{2}}}{2(1+x)^{\frac{3}{2}}} 解:有已知得F′(x)=f(x)f(x)⋅F(x)=2(1+x)2xex两边求积分∫f(x)⋅F(x)dx=∫2(1+x)2xexdxF2(x)=−∫xexd(1+x1)=1+xex+C因为F(0)=1,所以C=0因为x≥0时,F(x)>0,所以F(x)=1+xexf(x)=F′(x)=(1+xex)′=211+xex1⋅(1+x2)xex=2(1+x)23xe21
6 表格法积分
函数u(x),v(x),n+1阶可导u(x),v(x), n+1阶可导u(x),v(x),n+1阶可导
∫uv(n+1)dx反复使用分部积分可得∫uv(n+1)dx=∫udv(n)=uv(n)−∫u′v(n)dx=uv(n)−u′v(n−1)+∫u′′v(n−1)dx=uv(n)−u′v(n−1)+u′′v(n−2)−∫u′′′v(n−2)dx=uv(n)−u′v(n−1)+u′′v(n−2)+⋯+(−1)nu(n)v+(−1)n+1∫u(n+1)vdx\int{uv^{(n+1)}dx}反复使用分部积分可得\\ \int{uv^{(n+1)}dx}=\int{udv^{(n)}}=uv^{(n)}-\int{u^{'}v^{(n)}dx}\\ =uv^{(n)}-u^{'}v^{(n-1)}+\int{u^{''}v^{(n-1)}dx}\\ =uv^{(n)}-u^{'}v^{(n-1)}+u^{''}v^{(n-2)}-\int{u^{'''}v^{(n-2)}dx}\\ =uv^{(n)}-u^{'}v^{(n-1)}+u^{''}v^{(n-2)}+\cdots+(-1)^nu^{(n)}v+(-1)^{n+1}\int{u^{(n+1)}vdx} ∫uv(n+1)dx反复使用分部积分可得∫uv(n+1)dx=∫udv(n)=uv(n)−∫u′v(n)dx=uv(n)−u′v(n−1)+∫u′′v(n−1)dx=uv(n)−u′v(n−1)+u′′v(n−2)−∫u′′′v(n−2)dx=uv(n)−u′v(n−1)+u′′v(n−2)+⋯+(−1)nu(n)v+(−1)n+1∫u(n+1)vdx
表格如下:

例1 求∫(x3+2x)sinxdx\int{(x^3+2x)\sin xdx}∫(x3+2x)sinxdx
解:∫(x3+2x)sinxdx=−(x3+2x)cosx+(3x2+2)sinx+6xcosx−6sinx+C=(3x2−4)sinx−(x3−4x)cosx+C解:\int{(x^3+2x)\sin xdx}=-(x^3+2x)\cos x+(3x^2+2)\sin x+6x\cos x-6\sin x+C\\ =(3x^2-4)\sin x-(x^3-4x)\cos x+C 解:∫(x3+2x)sinxdx=−(x3+2x)cosx+(3x2+2)sinx+6xcosx−6sinx+C=(3x2−4)sinx−(x3−4x)cosx+C
例2 ∫e3xsin2xdx\int{e^{3x}\sin2xdx}∫e3xsin2xdx
解:∫e3xsin2xdx=−12e3xcos2x+34e3xsin2x−∫94e3xsin2xdx∫e3xsin2xdx=−213e3xcos2x+313e3xsin2x+C解:\int{e^{3x}\sin2xdx}=-\frac{1}{2}e^{3x}\cos2x+\frac{3}{4}e^{3x}\sin2x-\int{\frac{9}{4}e^{3x}\sin2xdx}\\ \int{e^{3x}\sin2xdx}=-\frac{2}{13}e^{3x}\cos2x+\frac{3}{13}e^{3x}\sin2x+C 解:∫e3xsin2xdx=−21e3xcos2x+43e3xsin2x−∫49e3xsin2xdx∫e3xsin2xdx=−132e3xcos2x+133e3xsin2x+C
7 有理函数求积分
例1 求∫x3+1x(x−1)3dx\int{\frac{x^3+1}{x(x-1)^3}dx}∫x(x−1)3x3+1dx
解:x3+1x(x−1)3=ax+b(x−1)3+c(x−1)2+dx−1通分得,a(x−1)3+bx+cx(x−1)+dx(x−1)2=x3+1计算得a=−1,b=2,c=1,d=2,所以∫x3+1x(x−1)3=∫(−1x+2x−1+1(x−1)2+2(x−1)3)dx=−ln∣x∣+2ln∣x−1∣−1x−1−1(x−1)2+C解:{\frac{x^3+1}{x(x-1)^3}}=\frac{a}{x}+\frac{b}{(x-1)^3}+\frac{c}{(x-1)^2}+\frac{d}{x-1}\\ 通分得,a(x-1)^3+bx+cx(x-1)+dx(x-1)^2=x^3+1\\ 计算得a=-1,b=2,c=1,d=2,所以\\ \int{\frac{x^3+1}{x(x-1)^3}}=\int{(\frac{-1}{x}+\frac{2}{x-1}+\frac{1}{(x-1)^2}+\frac{2}{(x-1)^3})dx}=-\ln|x|+2\ln|x-1|-\frac{1}{x-1}-\frac{1}{(x-1)^2}+C 解:x(x−1)3x3+1=xa+(x−1)3b+(x−1)2c+x−1d通分得,a(x−1)3+bx+cx(x−1)+dx(x−1)2=x3+1计算得a=−1,b=2,c=1,d=2,所以∫x(x−1)3x3+1=∫(x−1+x−12+(x−1)21+(x−1)32)dx=−ln∣x∣+2ln∣x−1∣−x−11−(x−1)21+C
例2 求∫2x+2(x−1)(x2+1)2dx\int{\frac{2x+2}{(x-1)(x^2+1)^2}dx}∫(x−1)(x2+1)22x+2dx
解:2x+2(x−1)(x2+1)2=ax−1+b1x+c1x2+1+b2x+c2(x2+1)2通分得,a(x2+1)2+(b1x+c1)(x−1)(x2+1)+(b2x+c2)(x−1)=2x+2计算得,a=1,b1=−1,c1=−1,b2=−2,c2=0∫2x+2(x−1)(x2+1)2=∫(1x−1−x+1x2+1−2x(x2+1)2)dx=ln∣x−1∣−12ln∣x2+1∣−arctanx+1x2+1+C解:\frac{2x+2}{(x-1)(x^2+1)^2}=\frac{a}{x-1}+\frac{b_1x+c_1}{x^2+1}+\frac{b_2x+c_2}{(x^2+1)^2}\\ 通分得,a(x^2+1)^2+(b_1x+c_1)(x-1)(x^2+1)+(b_2x+c_2)(x-1)=2x+2\\ 计算得,a=1,b_1=-1,c_1=-1,b_2=-2,c_2=0\\ \int{\frac{2x+2}{(x-1)(x^2+1)^2}}=\int{(\frac{1}{x-1}-\frac{x+1}{x^2+1}-\frac{2x}{(x^2+1)^2})dx}\\ =\ln|x-1|-\frac{1}{2}\ln|x^2+1|-\arctan x+\frac{1}{x^2+1}+C 解:(x−1)(x2+1)22x+2=x−1a+x2+1b1x+c1+(x2+1)2b2x+c2通分得,a(x2+1)2+(b1x+c1)(x−1)(x2+1)+(b2x+c2)(x−1)=2x+2计算得,a=1,b1=−1,c1=−1,b2=−2,c2=0∫(x−1)(x2+1)22x+2=∫(x−11−x2+1x+1−(x2+1)22x)dx=ln∣x−1∣−21ln∣x2+1∣−arctanx+x2+11+C
例3 求∫18−4sinx+7cosxdx\int{\frac{1}{8-4\sin x+7\cos x}dx}∫8−4sinx+7cosx1dx
令tanx2=t,x=2arctant,dx=21+t2∫18−4sinx+7cosxdx=∫18−42t1+t2+71−t21+t2⋅21+t2dt=∫(1t−5−1t−3)dt=ln∣t−5t−3∣+C=ln∣tanx2−5tanx2−3∣+C令\tan\frac{x}{2}=t,x=2\arctan t,dx=\frac{2}{1+t^2}\\ \int{\frac{1}{8-4\sin x+7\cos x}dx}=\int{\frac{1}{8-4\frac{2t}{1+t^2}+7\frac{1-t^2}{1+t^2}}\cdot\frac{2}{1+t^2}dt}\\ =\int{(\frac{1}{t-5}-\frac{1}{t-3})dt}=\ln|\frac{t-5}{t-3}|+C =\ln|\frac{\tan\frac{x}{2}-5}{\tan\frac{x}{2}-3}|+C 令tan2x=t,x=2arctant,dx=1+t22∫8−4sinx+7cosx1dx=∫8−41+t22t+71+t21−t21⋅1+t22dt=∫(t−51−t−31)dt=ln∣t−3t−5∣+C=ln∣tan2x−3tan2x−5∣+C
∫asinx+bcosxcsinx+dcosxdx=∫A(csinx+dcosx)+B(csinx+dcosx)′csinx+dcosxdx\int{\frac{a\sin x+b\cos x}{c\sin x+d\cos x}dx}=\int{\frac{A(c\sin x+d\cos x)+B(c\sin x+d\cos x)^{'}}{c\sin x +d\cos x}dx}∫csinx+dcosxasinx+bcosxdx=∫csinx+dcosxA(csinx+dcosx)+B(csinx+dcosx)′dx
例4 求∫4sinx+3cosx2sinx−cosxdx\int{\frac{4\sin x+3\cos x}{2\sin x-\cos x}dx}∫2sinx−cosx4sinx+3cosxdx
解:原式=∫a(2sinx−cosx)+b(2sinx−cosx)′2sinx−cosxdxa=1,b=2原式=x+22sinx−cosxd(2sinx−cosx)=x+2ln∣2sinx−cosx∣+C解:原式=\int{\frac{a(2\sin x-\cos x)+b(2\sin x-\cos x)^{'}}{2\sin x-\cos x}dx}\\ a =1,b=2\\ 原式=x+\frac{2}{2\sin x-\cos x}d(2\sin x-\cos x)=x+2\ln|2\sin x-\cos x|+C 解:原式=∫2sinx−cosxa(2sinx−cosx)+b(2sinx−cosx)′dxa=1,b=2原式=x+2sinx−cosx2d(2sinx−cosx)=x+2ln∣2sinx−cosx∣+C
后记
❓QQ:806797785
⭐️文档笔记地址:https://gitee.com/gaogzhen/math
参考:
[1]同济大学数学系.高等数学 第七版 上册[M].北京:高等教育出版社,2014.7.
[2]【梨米特】同济七版《高等数学》全程教学视频|纯干货知识点解析,应该是全网最细|微积分 | 高数[CP/OL].2020-04-16.p31.
相关文章:

0405习题总结-不定积分
文章目录1 不定积分的基本概念2 直接积分法-基本积分公式3 第一换元法-凑微分形式法4 第二类换元法5 分部积分求不定积分6 表格法积分7 有理函数求积分后记1 不定积分的基本概念 例1 f(x){x1,x≥012e−x12,x<0求∫f(x)dxf(x) \begin{cases} x1,\quad x\ge0\\ \frac{1}{2}e^…...

QT 常用控件类型命名参考
拟定的QT的控件命名规则:蛇形命名方式 控件类型开头,以下是QT控件类型命名的参考范例 Buttons Buttons起始字符串对象名称举例Push Buttonbuttonbutton_loginTool Buttontool_button / buttonbutton_switchRadio Buttonradio_button / radioradio_boy…...
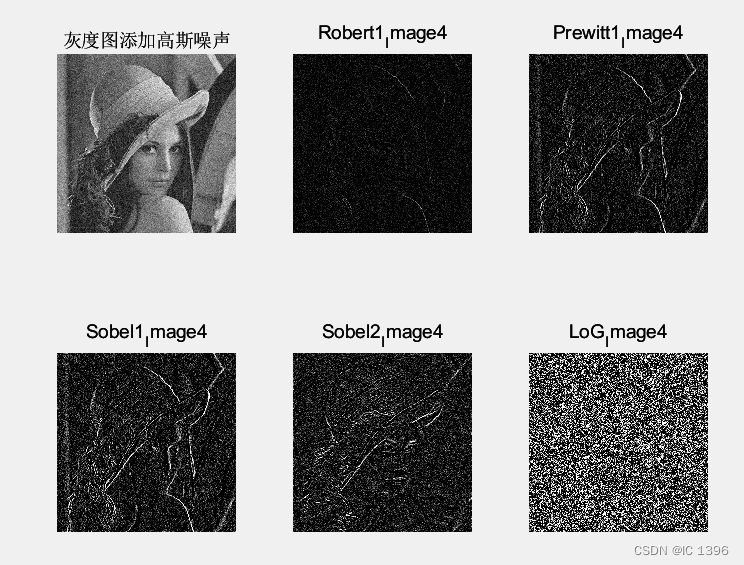
MATLAB与图像处理的那点小事儿~
目录 一、学习内容 二、matlab基本知识 三、线性点运算 四、非线性点运算,伽马矫正 五、直方图 1、直方图均衡化 (1)使用histep函数实现图像均衡化 (2)使用自行编写的均衡化函数实现图像均衡化 2、直方图规定…...
Java组个人题解)
第十四届蓝桥杯模拟赛(第三期)Java组个人题解
第十四届蓝桥杯模拟赛(第三期)Java组个人题解 今天做了一下第三期的校内模拟赛,有些地方不确定,欢迎讨论和指正~ 文章目录第十四届蓝桥杯模拟赛(第三期)Java组个人题解填空题部分第一题【最小数】第二题【E…...
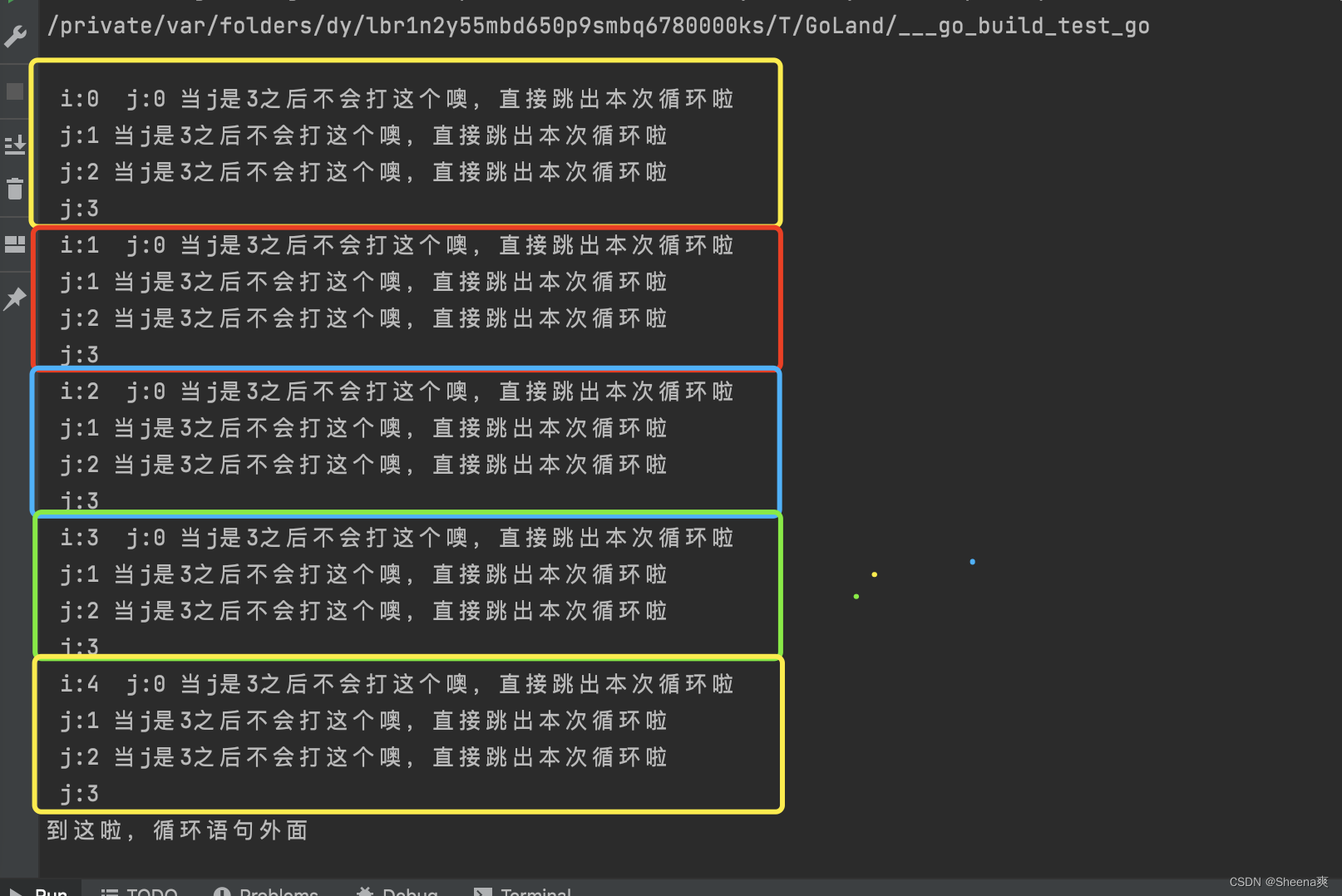
Go语言之条件判断循环语句(if-else、switch-case、for、goto、break、continue)
一、if-else条件判断语句 Go中的if-else条件判断语句跟C差不多。但是需要注意的是,Go中强制规定,关键字if和else之后的左边的花括号"{“必须和关键字在同一行,若使用了else if结构,则前段代码快的右花括号”}"必须和关…...
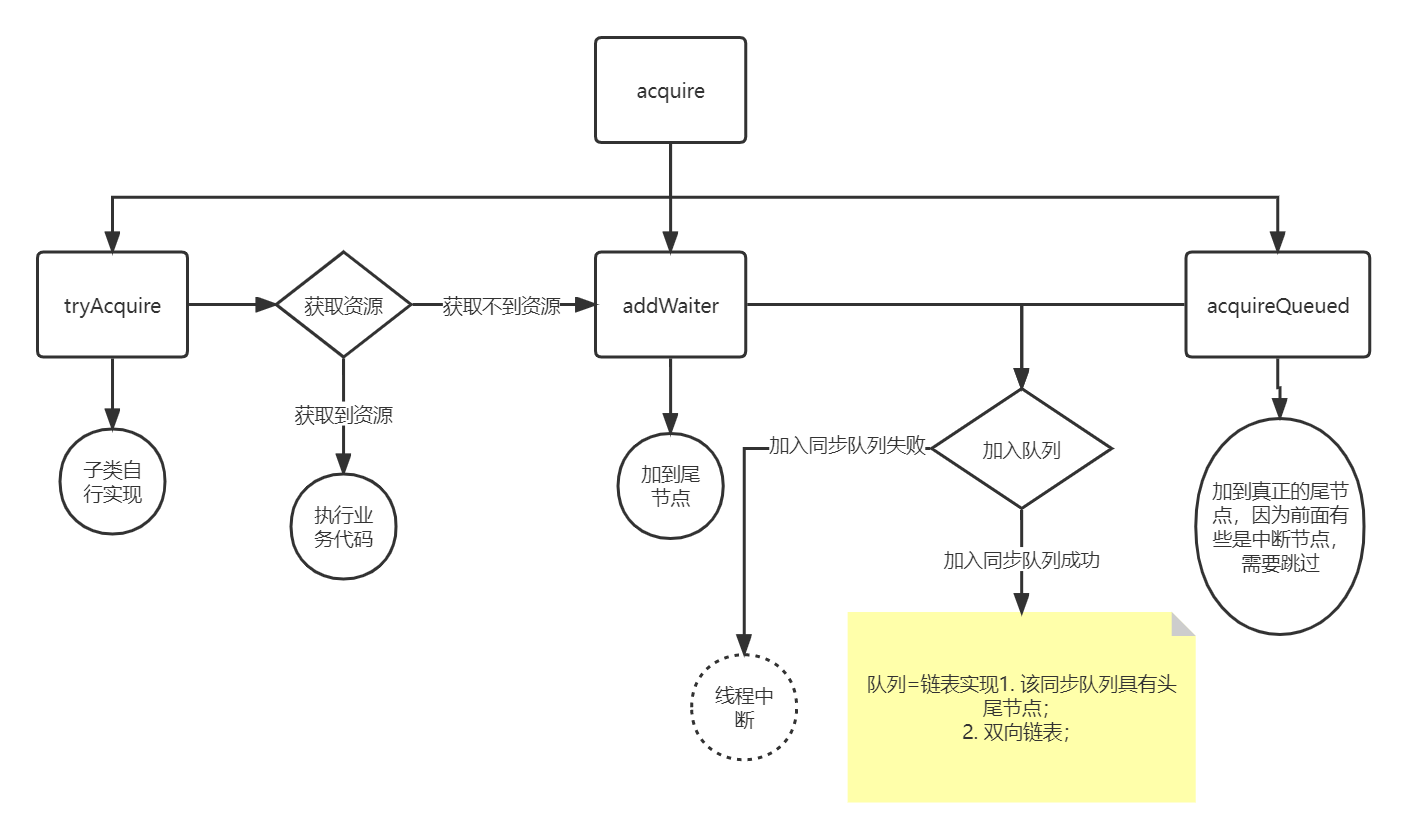
深入理解AQS
概念设计初衷:该类利用 状态队列 实现了一个同步器,更多的是提供一些模板方法(子类必须重写,不然会抛错)。 设计功能:独占、共享模式两个核心,state、Queue2.1 statesetState、compareAndSetSta…...
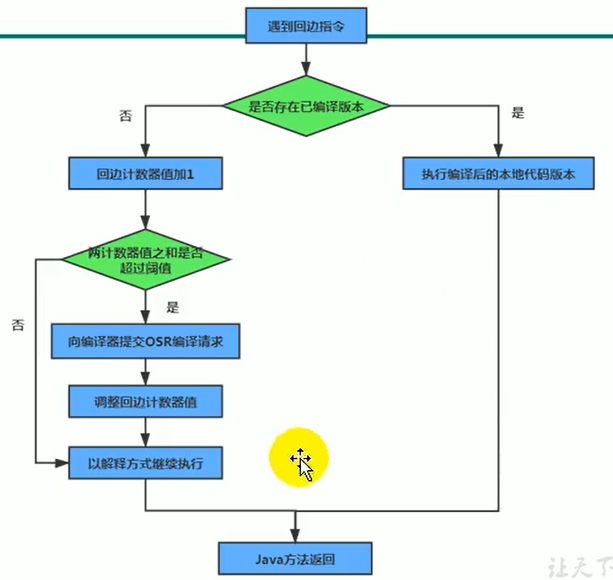
JVM学习笔记十:执行引擎
0. 前言 声明: 感谢尚硅谷宋红康老师的讲授。 感谢广大网友共享的笔记内容。 B站:https://www.bilibili.com/video/BV1PJ411n7xZ 本文的内容基本来源于宋老师的课件,其中有一些其他同学共享的内容,也有一些自己的理解内容。 1. …...
【2023-03-10】JS逆向之美团滑块
提示:文章仅供参考,禁止用于非法途径 前言 目标网站:aHR0cHM6Ly9wYXNzcG9ydC5tZWl0dWFuLmNvbS9hY2NvdW50L3VuaXRpdmVsb2dpbg 页面分析 接口流程 1.https://passport.meituan.com/account/unitivelogin主页接口:需获取下面的参数࿰…...

全志V853芯片放开快启方案打印及在快起方式下配置isp led的方法
全志V85x芯片 如何放开快启方案的打印? 1.主题 如何放开快启方案的打印 2.问题背景 产品:v851系列快启方案 软件:tina 其他:特有版本信息添加自由描述 (如固件版本,复现概率,特定环境&#x…...
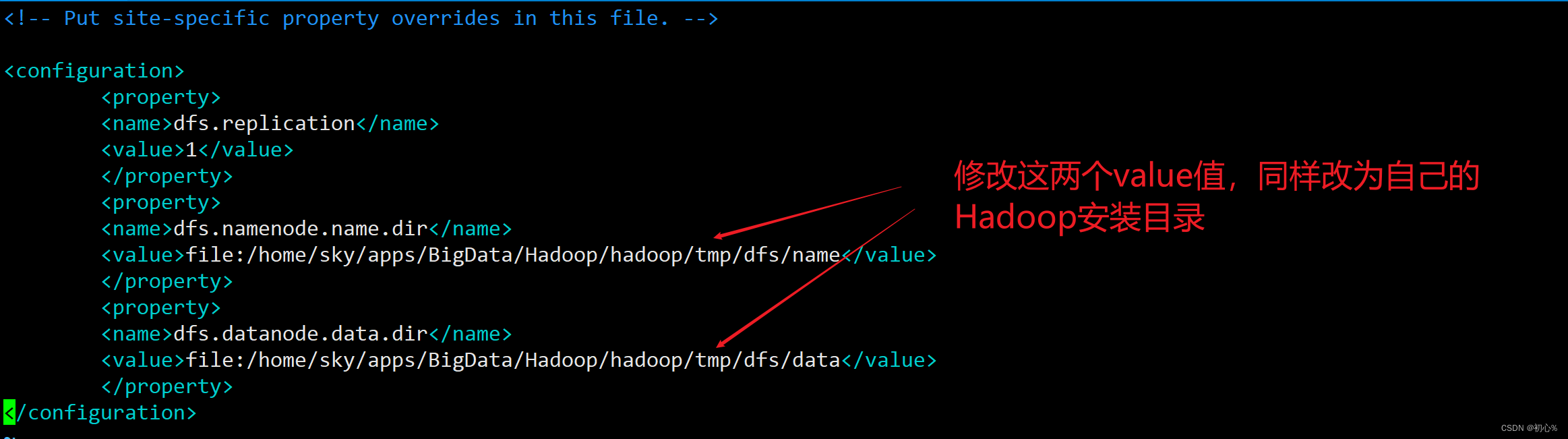
大数据 | (一)Hadoop伪分布式安装
大数据原理与应用教材链接:大数据技术原理与应用电子课件-林子雨编著 Hadoop伪分布式安装借鉴文章:Hadoop伪分布式安装-比课本详细 大数据 | (二)SSH连接报错Permission denied:SSH连接报错Permission denied 哈喽&a…...

Django/Vue实现在线考试系统-06-开发环境搭建-Django安装
1.0 基本介绍 Django 是一个由 Python 编写的一个开放源代码的 Web 应用框架。 使用 Django,只要很少的代码,Python 的程序开发人员就可以轻松地完成一个正式网站所需要的大部分内容,并进一步开发出全功能的 Web 服务 Django 本身基于 MVC 模型,即 Model(模型)+ View(…...
KaiwuDB 时序引擎数据存储内存对齐技术解读
一、理论1、什么是内存对齐现代计算机中内存空间都是按照 byte 划分的,在计算机中访问一个变量需要访问它的内存地址,从理论上看,似乎对任何类型的变量的访问都可以从任何地址开始。但在实际情况中,通常在特定的内存地址才能访问特…...
IR 808 Alkyne,IR-808 alkyne,IR 808炔烃,近红外吲哚类花菁染料
【产品理化指标】:中文名:IR-808炔烃英文名:IR-808 alkyne,Alkyne 808-IR CAS号:N/AIR-808结构式:规格包装:10mg,25mg,50mg,接受各种复杂PEGS定制服务&#x…...
elasticsearch
这里写目录标题1.初识ElasticSearch1.1 了解ES1.2 倒排索引1.2.1 正向索引1.2.2 倒排索引1.2.3 正向和倒排1.3 ES的一些概念1.3.1 文档和字段1.3.2 索引和映射1.3.3 mysql和elasticsearch1.4 安装ES、kibana1.初识ElasticSearch 1.1 了解ES elasticsearch是一款非常强大的开源…...
并发编程---java锁
java锁一 多线程锁synchronized案例分析1.1synchronized介绍1.2 synchronized案例分析1.2.1.标准访问,请问先打印邮件还是短信?1.2.2.邮件⽅法暂停4秒钟,请问先打印邮件还是短信?分析1.2.3.新增⼀个普通⽅法hello(&…...

品牌营销 | 学习如何最大限度地发挥品牌营销的作用
您是否想过如何最大限度地发挥品牌营销的潜力?这是一项艰巨的挑战,通过了解品牌营销的基本组成部分,您可以成功地推广您的品牌。 (图源:Pixabay) 品牌营销的基本组成部分 你需要做什么来发展稳固的品牌&am…...
Linux驱动的同步阻塞和同步非阻塞
在字符设备驱动中,若要求应用与驱动同步,则在驱动程序中可以根据情况实现为阻塞或非阻塞一、同步阻塞这种操作会阻塞应用程序直到设备完成read/write操作或者返回一个错误码。在应用程序阻塞这段时间,程序所代表的进程并不消耗CPU的时间&…...

LearnOpenGL-光照-5.投光物
本人刚学OpenGL不久且自学,文中定有代码、术语等错误,欢迎指正 我写的项目地址:https://github.com/liujianjie/LearnOpenGLProject 文章目录投光物平行光点光源聚光不平滑的例子平滑例子投光物 前面几节使用的光照都来自于空间中的一个点 即…...

【C语言】每日刷题 —— 牛客语法篇(1)
前言 大家好,今天带来一篇新的专栏c_牛客,不出意外的话每天更新十道题,难度也是从易到难,自己复习的同时也希望能帮助到大家,题目答案会根据我所学到的知识提供最优解。 🏡个人主页:悲伤的猪大…...

【深度学习】Subword Tokenization算法
在自然语言处理中,面临的首要问题是如何让模型认识我们的文本信息,词,是自然语言处理中基本单位,神经网络模型的训练和预测都需要借助词表来对句子进行表示。 1.构建词表的传统方法 在字词模型问世之前,做自然语言处理…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

大数据学习栈记——Neo4j的安装与使用
本文介绍图数据库Neofj的安装与使用,操作系统:Ubuntu24.04,Neofj版本:2025.04.0。 Apt安装 Neofj可以进行官网安装:Neo4j Deployment Center - Graph Database & Analytics 我这里安装是添加软件源的方法 最新版…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

智能在线客服平台:数字化时代企业连接用户的 AI 中枢
随着互联网技术的飞速发展,消费者期望能够随时随地与企业进行交流。在线客服平台作为连接企业与客户的重要桥梁,不仅优化了客户体验,还提升了企业的服务效率和市场竞争力。本文将探讨在线客服平台的重要性、技术进展、实际应用,并…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...
