Easy Deep Learning——池化层
池化是什么?它有什么作用?
还是草地的场景,把草地分成一块块的网格,数量还是太多了,如何继续简化输入数据呢?
这时候可以只取一块网格中所有的小草的大小形状的平均值或者最大值作为一个输入数据,这样就大大简化了数据数量。
池化(Pooling)是卷积神经网络中的一种常用操作,其目的是通过减小特征图的空间大小来降低模型的复杂度。在池化操作中,我们将特征图划分为多个子区域,然后对每个子区域进行聚合操作,生成一个较小的特征图。
通常,池化操作的聚合操作可以是取最大值(Max Pooling)、取平均值(Average Pooling)等,其中最大值池化是最常用的一种。
池化的作用有以下几点:
-
减小特征图的空间大小,降低模型复杂度,减少计算量。
-
增强模型对平移不变性的学习能力,即使目标在图像中稍微移动一点,也能保持对它的识别能力。
-
缓解过拟合,减少模型对噪声的敏感性,提高模型的泛化能力。
在实际应用中,池化操作通常会与卷积操作交替进行,以构建一个完整的卷积神经网络。同时,由于池化操作的缩小特征图的空间大小,因此在池化操作之前,可以通过增加卷积层的数量或通道数来提高模型的表达能力,从而保持对目标的识别能力。
Pytorch中常用的池化操作的函数

还是上一篇的例子,我们把每一个卷积核的结果进行最大值或平均值池化,可得到如下结果

这样数据量明显减小。以下是python代码
import numpy as np
import torch
import torch.nn as nn
import matplotlib.pyplot as plt
from PIL import Image# 读取图像并将其转换为灰度图
img = Image.open("/home/cbc/图片/2.png")
imgGray = np.array(img.convert("L"), dtype=np.float32) # convert("L") 转换为单通道图片imh,imw = imgGray.shape
# 将二维的灰度图像转换成四维的张量,维度为(1, 1, imh, imw),表示一个batch,一个通道,高为imh,宽为imw
imgGray_torch = torch.from_numpy(imgGray.reshape((1,1,imh,imw)))
print(imgGray_torch.shape)
# 定义卷积核大小和卷积核矩阵,其中心为24,其余为-1
kersize = 5
ker = torch.ones(kersize, kersize, dtype=torch.float32) * -1
ker[2, 2] = 24
ker = ker.reshape((1, 1, kersize, kersize))# 将卷积核矩阵转换成张量,维度为(1, 1, kersize, kersize),表示一个batch,一个通道,卷积核的高和宽分别为kersize
ker = ker.reshape((1, 1, kersize, kersize))# 定义一个2D卷积层,输入通道数为1,输出通道数为2,卷积核的大小为(kersize,kersize),不使用偏置项
conv2d = nn.Conv2d(1, 2, (kersize, kersize), bias=False)# 将卷积核张量赋值给卷积层的权重,第一个通道的权重为ker
conv2d.weight.data[0] = ker# 对灰度图像进行卷积操作
imconv2dout = conv2d(imgGray_torch)
maxpoll2 = nn.MaxPool2d(2,stride=2)
pool2_out = maxpoll2(imconv2dout)# 将卷积和池化的结果的张量降维成二维数组
imconv2dout_im = pool2_out.data.squeeze()# 打印卷积结果的形状
print("卷积后的尺寸:", imconv2dout_im.shape)# 绘制卷积结果的两个通道
plt.figure(figsize=(12, 6))
plt.subplot(1, 2, 1)
plt.imshow(imconv2dout_im[0], cmap=plt.cm.gray)
plt.axis(False)
plt.subplot(1, 2, 2)
plt.imshow(imconv2dout_im[1], cmap=plt.cm.gray)
plt.axis(False)
plt.show()

可以看出,由于池化后的输入数据量减少,图像也变得模糊了。
相关文章:

Easy Deep Learning——池化层
池化是什么?它有什么作用? 还是草地的场景,把草地分成一块块的网格,数量还是太多了,如何继续简化输入数据呢? 这时候可以只取一块网格中所有的小草的大小形状的平均值或者最大值作为一个输入数据,这样就大…...

TryHackMe-VulnNet: Active(ez 域渗透)
VulnNet: Active VulnNet Entertainment在他们以前的网络中遇到了不好的时光,该网络遭受了多次破坏。现在,他们移动了整个基础架构,并再次聘请您作为核心渗透测试人员。您的目标是获得对系统的完全访问权限并破坏域。 这应该是我在thm打的最…...
TencentOS Server 安装 PostgreSQL
TencentOS 简介 2019 年,随着腾讯公司外部客户的需求,以及公司开源协同战略的推进,tlinux 对外开源并进行了品牌升级,升级为 TencentOS Server。TencentOS 包含三大场景,分别如下: TencentOS Server&…...
多线程的风险 --- 线程安全
✨个人主页:bit me👇 ✨当前专栏:Java EE初阶👇 ✨每日一语:低头赶路,敬事如仪;自知自心,其路则明。 目 录🍸一. 线程不安全🍹二. 线程不安全的原因…...

Linux信号详解
文章目录Linux信号什么是信号**从生活角度理解: **技术应用角度的信号进程的注意事项信号概念用kill -l命令可以察看系统定义的信号列表信号处理常见方式概览信号产生通过终端按键产生信号使用signal函数自定义SIGINT信号的处理方式使用sigprocmask函数阻塞2号信号和40号信号vo…...

JAVA使用POI操作EXCEL
设置公式totalRow.createCell(4).setCellFormula("SUM(E9:E35");// 执行公式wb.setForceFormulaRecalculation(true);合并单元格sheet.addMergedRegion(new CellRangeAddress(0, 0, 3, 7));单元格格式CellStyle cellStyle wb.createCellStyle();// 字体XSSFFont fon…...

只做笔记有必要买apple pencil吗?苹果笔的代替笔推荐
如果仅仅使用IPAD来进行打游戏和看剧的话,未免有些浪费。ipad的作用还是挺大的,可以用来做学习笔记,也可以用来做绘画,也可以用来做一些重要的内容。很多人都会认为,苹果的电容笔很好用,但是价格上要比一般…...
Hive---sqoop安装教程及sqoop操作
sqoop安装教程及sqoop操作 文章目录sqoop安装教程及sqoop操作上传安装包解压并更名添加jar包修改配置文件添加sqoop环境变量启动sqoop操作查看指定mysql服务器数据库中的表在hive中创建一个teacher表跟mysql的mysql50库中的teacher结构相同将mysql中mysql50库中的sc数据导出到h…...

【C++】register 关键字
文章目录一. 什么是寄存器?二. 为什么要存在寄存器?三. register 修饰变量一. 什么是寄存器? 我们都知道,CPU主要是负责进行计算的硬件单,但是为了方便运算,一般第一步需要先把数据从内存读取到CPU内&…...

剑指 Offer II 024. 反转链表
题目链接 剑指 Offer II 024. 反转链表 easy 题目描述 给定单链表的头节点 head,请反转链表,并返回反转后的链表的头节点。 示例 1: 输入:head [1,2,3,4,5] 输出:[5,4,3,2,1] 示例 2: 输入:h…...

从Linux内核中学习高级C语言宏技巧
Linux内核可谓是集C语言大成者,从中我们可以学到非常多的技巧,本文来学习一下宏技巧,文章有点长,但耐心看完后C语言level直接飙升。 本文出自:大叔的嵌入式小站,一个简单的嵌入式/单片机学习、交流小站 从…...

详解Python的装饰器
Python中的装饰器是你进入Python大门的一道坎,不管你跨不跨过去它都在那里。 为什么需要装饰器 我们假设你的程序实现了say_hello()和say_goodbye()两个函数。 def say_hello():print "hello!"def say_goodbye():print "hello!" # bug hereif…...

k8s-Pod域名学习总结
k8s-Pod域名学习总结 大纲 k8s内置DNS服务 配置Pod的域名服务 CornDNS配置 默认Pod的域名 自定义Pod的域名 实战需求 1 Pod有自己的域名 2 集群内部的Pod可以通过域名访问其他的Pod 基础准备: 1 k8s 集群版本1.17 k8s内置DNS服务 k8s1.17安装完成后自动创建…...

0405习题总结-不定积分
文章目录1 不定积分的基本概念2 直接积分法-基本积分公式3 第一换元法-凑微分形式法4 第二类换元法5 分部积分求不定积分6 表格法积分7 有理函数求积分后记1 不定积分的基本概念 例1 f(x){x1,x≥012e−x12,x<0求∫f(x)dxf(x) \begin{cases} x1,\quad x\ge0\\ \frac{1}{2}e^…...

QT 常用控件类型命名参考
拟定的QT的控件命名规则:蛇形命名方式 控件类型开头,以下是QT控件类型命名的参考范例 Buttons Buttons起始字符串对象名称举例Push Buttonbuttonbutton_loginTool Buttontool_button / buttonbutton_switchRadio Buttonradio_button / radioradio_boy…...
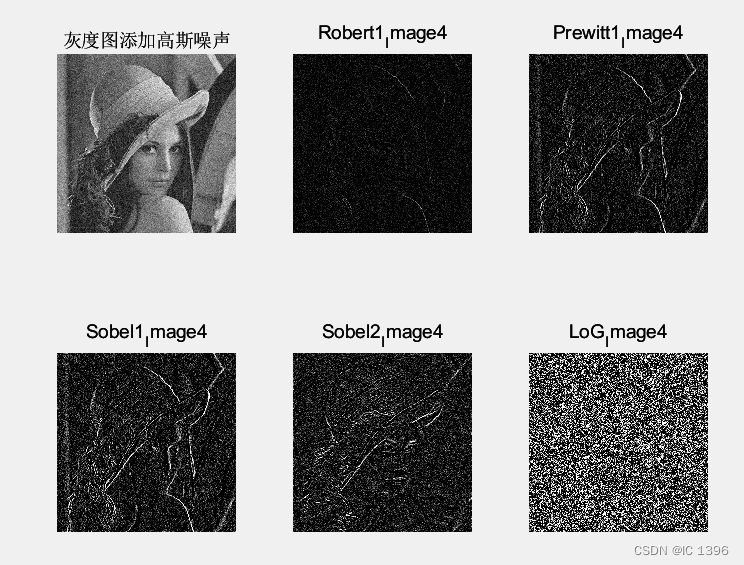
MATLAB与图像处理的那点小事儿~
目录 一、学习内容 二、matlab基本知识 三、线性点运算 四、非线性点运算,伽马矫正 五、直方图 1、直方图均衡化 (1)使用histep函数实现图像均衡化 (2)使用自行编写的均衡化函数实现图像均衡化 2、直方图规定…...
Java组个人题解)
第十四届蓝桥杯模拟赛(第三期)Java组个人题解
第十四届蓝桥杯模拟赛(第三期)Java组个人题解 今天做了一下第三期的校内模拟赛,有些地方不确定,欢迎讨论和指正~ 文章目录第十四届蓝桥杯模拟赛(第三期)Java组个人题解填空题部分第一题【最小数】第二题【E…...
Go语言之条件判断循环语句(if-else、switch-case、for、goto、break、continue)
一、if-else条件判断语句 Go中的if-else条件判断语句跟C差不多。但是需要注意的是,Go中强制规定,关键字if和else之后的左边的花括号"{“必须和关键字在同一行,若使用了else if结构,则前段代码快的右花括号”}"必须和关…...
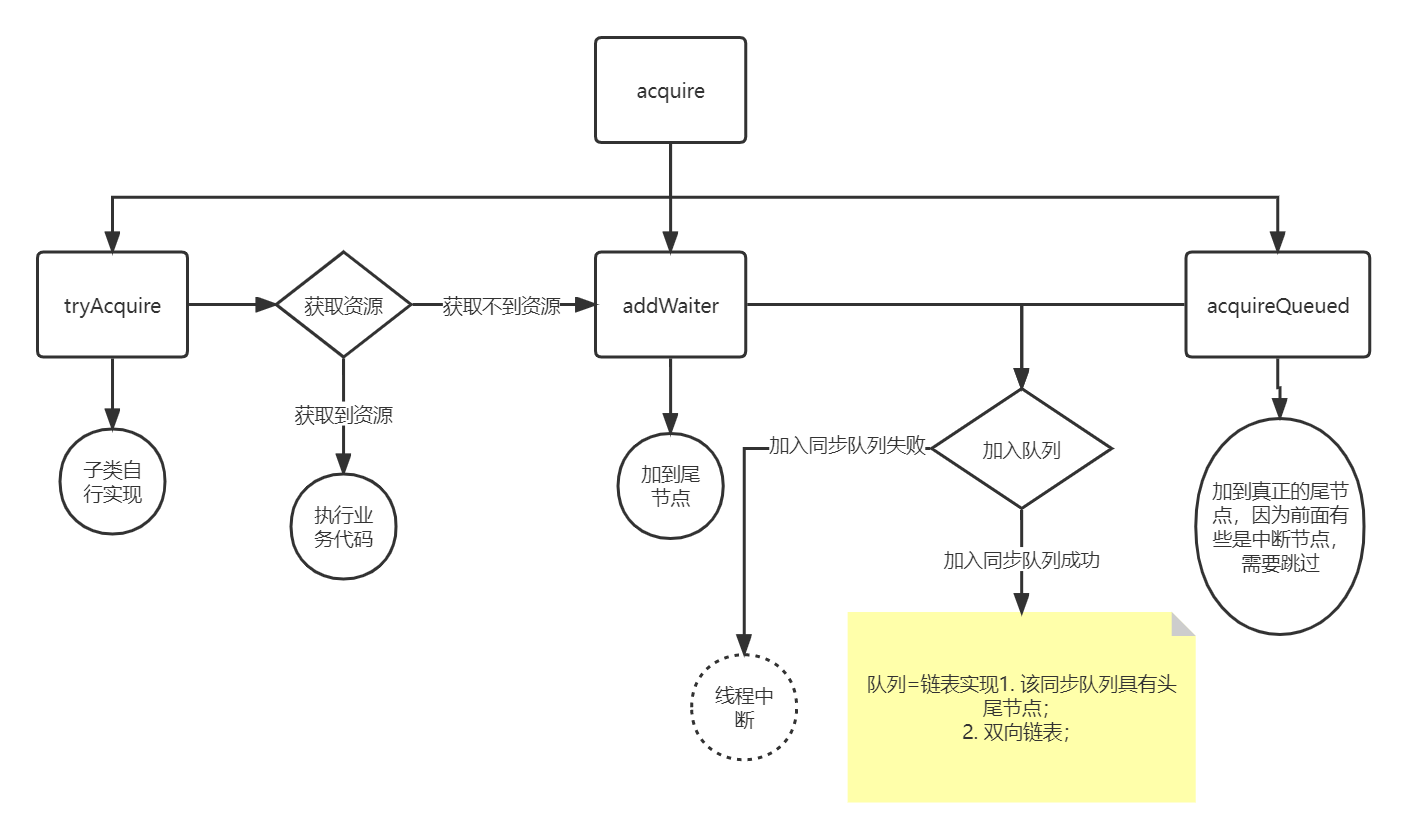
深入理解AQS
概念设计初衷:该类利用 状态队列 实现了一个同步器,更多的是提供一些模板方法(子类必须重写,不然会抛错)。 设计功能:独占、共享模式两个核心,state、Queue2.1 statesetState、compareAndSetSta…...
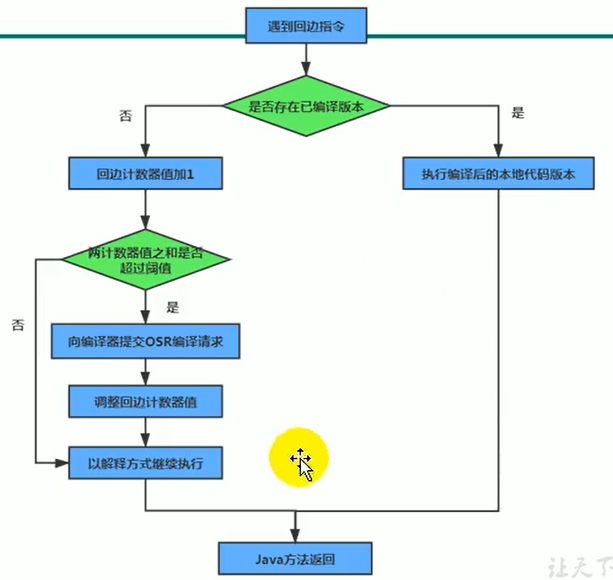
JVM学习笔记十:执行引擎
0. 前言 声明: 感谢尚硅谷宋红康老师的讲授。 感谢广大网友共享的笔记内容。 B站:https://www.bilibili.com/video/BV1PJ411n7xZ 本文的内容基本来源于宋老师的课件,其中有一些其他同学共享的内容,也有一些自己的理解内容。 1. …...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

Keil 中设置 STM32 Flash 和 RAM 地址详解
文章目录 Keil 中设置 STM32 Flash 和 RAM 地址详解一、Flash 和 RAM 配置界面(Target 选项卡)1. IROM1(用于配置 Flash)2. IRAM1(用于配置 RAM)二、链接器设置界面(Linker 选项卡)1. 勾选“Use Memory Layout from Target Dialog”2. 查看链接器参数(如果没有勾选上面…...

高危文件识别的常用算法:原理、应用与企业场景
高危文件识别的常用算法:原理、应用与企业场景 高危文件识别旨在检测可能导致安全威胁的文件,如包含恶意代码、敏感数据或欺诈内容的文档,在企业协同办公环境中(如Teams、Google Workspace)尤为重要。结合大模型技术&…...

【单片机期末】单片机系统设计
主要内容:系统状态机,系统时基,系统需求分析,系统构建,系统状态流图 一、题目要求 二、绘制系统状态流图 题目:根据上述描述绘制系统状态流图,注明状态转移条件及方向。 三、利用定时器产生时…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...
